中心粒子群优化算法

王 丹（辽宁理工学院，121000）

中心粒子群优化算法

王 丹
（辽宁理工学院，121000）

在线性递减权重粒子群优化算法（LDWPSO）中提到了中心粒子这一概念，进而提出了中心粒子群优化算法(中心PSO)。在线性递减权重粒子群优化算法中，中心粒子不像其它一般的粒子，中心粒子没有明确的速度，并且被始终置于粒子群的中心。此外，在神经网络训练算法中比较中心粒子群优化算法和线性递减权重粒子群优化算法，结果表明：中心粒子群优化算法的性能优于线性递减权重粒子群优化算法。

粒子群优化算法；神经网络；进化计算

0 引言

粒子群优化算法是模仿鸟群和鱼群的社会行为而出现的一种进化的计算技术，因为粒子群优化算法在非线性函数优化中具有较好的收敛性和很好的性能，得到了人们的极大关注。许多研究人员致力于用各种不同的方法和各种先进有趣的变量来改善他的性能。这些方法大致分如下几类。

改进的方法是给粒子群算法的速度和位置方程中增加新的系数，并且这个系数要进行合理的挑选。Angeline指出基本粒子群算法局部搜索能力很低。为了克服这个缺点，Shi 和Eberhart提出了线性递减权重粒子群算法，此算法把线性递减惯性因子引入到基本粒子群算法的速度更新方程中。因为惯性因子有效的平衡了粒子群的全局和局部搜索能力，使得粒子群算法的性能得到了极大的改善。

粒子群算法的一个关键特色是区域内的粒子间的社会信息共享。因此人们提出各种不同的信息共享方式来改善该算法的性能。Kennedy研究了各种影响该算法性能的拓扑结构，并指出von Neumann拓扑结构性能更好。Suganthan提出了一个可变邻域，在优化的最初时期，邻域是单个粒子自身的邻域，随这粒子代数的增长，邻域逐渐延伸到所有的粒子。Mohai提出了一种动态适应邻域，用这种邻域动态适应邻域可以随意产生，直接构建原始值种群的拓扑结构，在种群运行过程中种群结构的边缘可随意从一个点移动到另一个点。Lovbjerg 等人将基本粒子群算法与分组饲养的观点结合在一起。张和谢将微分演化算子引入到基本粒子群算法中。Krink和Lovbjerg将基本粒子群算法和遗传算法结合在一起。

1 中心粒子群优化算法

1.1 线性递减权重粒子群算法

一个种群由N个在D维搜索空间中运动的粒子构成。第i个粒子在第t次迭代中的位置记为,速度记为，个体粒子所达到的个体极值点记为，群中所有粒子所达到的全局极值点记为。第i个例子在下一次迭代中的位置将由下列方程计算得到

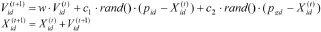
1.2 中心粒子群优化算法

中心离子群算法发展的动力来源于人们对种群行为的观察。由方程（1）可知，粒子的速度由先前的速度和个体认知能力和社会认知能力决定。由于社会认知（方程的第三部分）是指所有粒子都被全局最优吸引并且朝着它移动。而另外两部分，先前的速度和个体认知能力相当于自制特性，使粒子保持他们自己的信息。因此，在搜索期间，所有的粒子都朝着全局最优位置移动，但它们的位置常常不同又接近全局最优位置。

论文中明确提出中心粒子在每次迭代中位于种群的中心。在粒子群中另外的N-1个例子在每次迭代中使用基本粒子群算法更新它们的位置，而中心粒子采用下列方程更新它的位置：

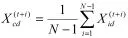
不像其它的粒子，中心粒子没有速度，它除过粒子计算之外，像其他所有例子一样参与所有的过程，例如适应值计算，竞争最好粒子等。此算法叫做中心粒子群优化算法。中心粒子群算法的伪代码定义如下：

开始粒子群算法

初始化（）；

T从1到 最大迭代次数

I从1到N-1

根据方程（更新位置）；

结束

更新中心离子的位置；

结束

结束粒子群优化算法

正如上面提到的中心粒子具有潜在的有效解。如果中心粒子得结果仅仅是使它去寻找好的位置，它就不会极大的影响算法的性能。一个粒子太少是没法与种群中的其它一般的粒子比较的。更重要的是中心粒子更有可能成为种群的社会极值。因此中心粒子能够引导整个种群的未来的区域并且能够加速收敛。

2 实验

2.1 函数优化

我们的实验中要用到三个基准函数（都是最小化）第一个函数是Rosenbrock函数：

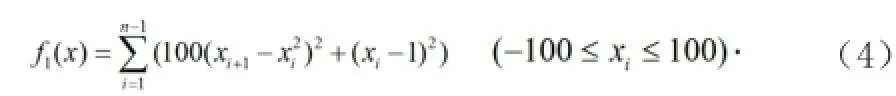
第二个函数是广义Rosenbrock函数：

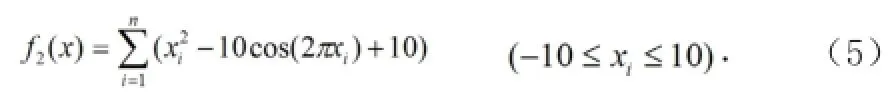
第三个函数是广义Griewank函数：

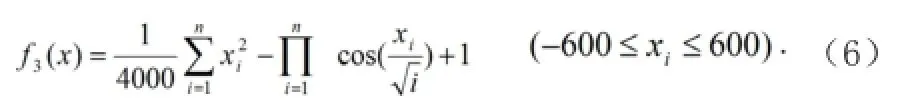
在我们的实验中对线性递减权重粒子群算法和中心粒子去算法进行了比较。对这两种算法制定相同的参数：惯性权重从0.9线性递减到0.4；学习因子；等于；等于；每个方程用10，20，30的规模去检测；相应的最大迭代次数被分别设为1000.1500和2000。为了检测算法的可测量性，用四个种群（大小为N=20，40，80，160）对每个函数的不同维数进行检测。中心粒子群算法包括一个中心粒子和N-1个普通粒子。在每个实验中，对每个算法执行100次。

2.2 神经网络训练

神经网络训练是一个复杂优化问题。通常，目标是所有训练模式的均方误差。可变因子包括权重和偏重值。假设一个标准的网络结构用D表示驶入单元，用M表示隐藏单元，用C表示输出单元，可变因子的数目总之，神经网络训练是一个具有多个局部最小值的多空间优化问题。

神经网络训练用 n份随机划分技术将数据划分成大小相等的n份互斥数据。选出一组数据作为数据组，其他的组作为测试组。在我们的实验中设定n为10.对人物分类采用S型转移函数的三层前馈神经网络 。对于神经网络被设置为14个输入 单元，5个隐藏单元，2个输出单元，因此每个粒子的维数是87。对于糖尿病，神经网络被设置为8个输入单元，5个隐藏单元，2个输出单元，因此每个粒子的维数是57。在上述实验的函数优化中，中心粒子群算法和线性递减权重粒子群算法的所有参数除过之外，其他都是相同的。最大迭代次数被设置为1000，种群大小被设置为20.

3 结论

论文中我们提出了中心粒子群算法，而其中的中心粒子这一概念是从线性递减权重粒子群算法中引进的。种群由普通的粒子组成，在每次迭代中中心粒子的位置随着种群中心的改变而改变。在典型的粒子活动中，所有的粒子围绕种群的中心摆动，并且逐渐趋于种群的中心。在运行过程中，中心粒子通常能获得较好的位置而且变成全局最优粒子，因此虽然中心粒子只有一个，它有更多的机会去引导种群的搜索并且极大的影响算法的性能。实验结果表明中心粒子群算法的性能比线性递减权重粒子群算法的性能要好。

[1] P.J.Angeline,Evolutionary optimization versus particle swarmoptimization:philosophy and performancedifferences,Lecture Notesin Computer Sc ience,vol.1447,Springer,Berlin,1998,pp.601-610.

[2] P.J.Angeline,Using selection to improve particle swarm optimization,Proceedings of the IEEE Conference on Evolutionary Computation,1998,pp. 84-89.

[3] R.Eberhart,Y.Shi,Comparing inertia weights and constrictionfactors in particle swarm optimization,Proceedings of the IEEE Conference on Evolutionary Computation,2000,pp.84-88.

[4] M.Clerc,J.Kennedy,The particle swarm-explosion, stability,andconvergence in a multidimensional complex space,IEEE Trans.Evol.Comput.6 (2002) 58-73.

[5] S.Baskar,P.Suganthan,A novel concurrent particle swarmoptimization,Proceedings of the Congress on Evolutionary Computation,2004,pp.792-796.

[6] C.Blake,C.J.Merz,UCI repository of machine learning databases,1998.

[7] S.C.Esquivel,C.A.Coello Coello,On the use of particle swarm optimization with multimodal functions,Proceedings of the Congress on Evolutionary Computation,2003,pp.1130-1136.

王丹，女，1981年11月，讲师，所学专业：计算机科学与技术，现研究方向：计算机教学

Center particle swarm optimization algorithm

Wang Dan
（Liaoning Institute of Technology 121000）

The linear decreasing weight particle swarm optimization algorithm (LDWPSO) is mentioned in the concept of a center particle,and then puts forward center particle swarm optimization algorithm (PSO). The linear decreasing weight particle swarm optimization algorithm, unlike other general center particle particle, particle velocity center is not clear, and is always placed in the center of the particle swarm. In addition, the neural network training algorithm compared to particle swarm optimization algorithm and the linear decreasing weight particle swarm optimization algorithm, results show that: the performance is better than the linear optimization center particle swarm decreasing weight particle swarm optimization algorithm.

particle swarm optimization algorithm；neural network；evolutionary computation