橡胶芯夹层板隔声特性研究

王康乐，温华兵，陆金铭，彭子龙

(江苏科技大学振动噪声研究所，江苏 镇江 212003)

夹层板具有优良的力学特性和隔声性能，现已被广泛用于舰船、列车和航空等的外壳、底板等结构。国内学者对其结构和阻尼特性作了深入的研究[1―3]，但其声学特性复杂，特别涉及到复杂环境下的声振耦合，因此对其声学特性进行研究具有重要的现实意义。

目前研究夹层板振动特性的理论主要有：Reissner理论、Hoff理论和∏pycako B―杜庆华理论[4]。国内外学者都对其声学特性做过一些研究。国外，早期Simon和Pauzin[5]建立了无限大厚夹芯三明治板在扩散声场中的数学模型。考虑到实际尺寸情况，Lee和Kondo[6]提出了有限尺寸的三明治板的声学模型。近期，Assaf[7]基于Hamilton原理研究了芯层厚度、损耗因子和温度等因素对夹层板隔声量的影响。国内，丁晓等[8]通过实验研究表明：泡沫铝复合板具有较好的低频吸声性能，在0.5～1 kHz频率范围吸声系数提高较大。何祚镛[9]对声激励下薄板的声辐射特性进行了深入研究。在声激励下，对镶嵌在无限大刚性平面障板上的简支薄板，在其激励域内考虑了反射声压、辐射声压，而在其接收域内只考虑了辐射声压。任树伟等[10]基于夹层板的Reissner理论推导了蜂窝夹层板隔声量的表达式，最后采用数值方法对理论进行了验证。但对薄芯层的夹层板，Reissner理论没考虑表层的抗弯刚度。同时，国内研究单个平面声源下夹层板的隔声量的文献较多，而研究混合声场下夹层板的隔声量的文献不多见。

考虑了面板抗弯刚度的影响，由Hoff理论得到夹层板振动方程，根据声学机理，建立了夹层板的声振耦合方程，结合流-固耦合边界条件，求解了声振耦合系统方程。再根据声学特性，建立了夹层板在混合声场下的隔声量表达式。用数值方法对四边简支的橡胶夹层板进行了声学数值模拟，讨论橡胶层的材料损耗因子、厚度、弹性模量，以及平面尺寸对夹层板隔声量的影响。

1 夹层板隔声量的理论模型

假定夹层板镶嵌在无限大刚性平面障板上，这样障板就把空气域分隔为两个部分，即激励域和接收域。一个平面波以入射角θ，方位角φ入射到三明治板上，则在z<0半空间除入射波和反射波之外，还应考虑有限板在声激励下振动辐射的声波；而在z>0半空间只存在辐射声波，如图1所示。

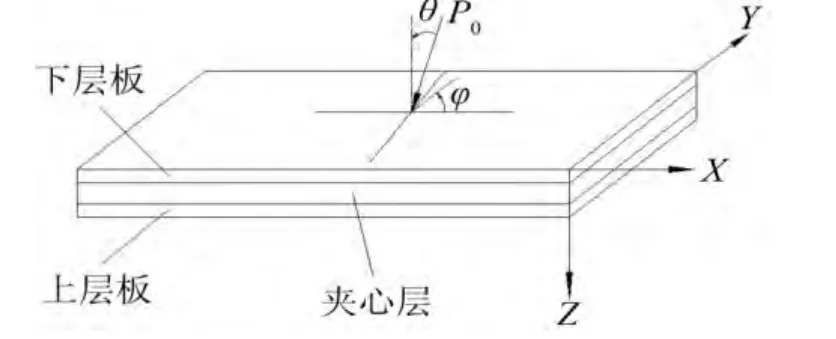
图1 夹层板结构示意图

设入射波声压

其中p0是入射声压幅值，ω是入射波圆频率；k=ω/c是空气中的波数；

其中kx=ksinθcosφ，ky=ksinθsinφ，kz=kcosθ分别为x,y,z三个方向的波数。

在夹层板的另一侧存在透射声压

在空气—板的交界面上，应满足z向连续性条件

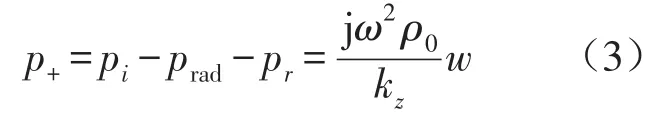
由式(2)和式(3)可知

所以入射侧声压p-(z=0)，透射声压p+为

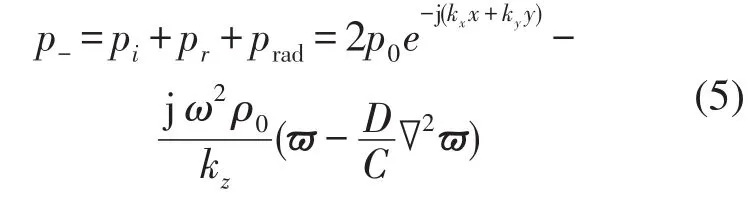
根据Hoff定理，夹层板的振动方程[4]为

对矩形夹层板四边简支情况，其简正模式分布函数为

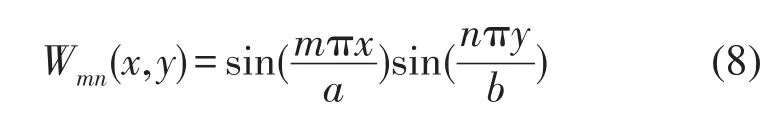
夹层板无阻尼自由振动时的位移函数为：

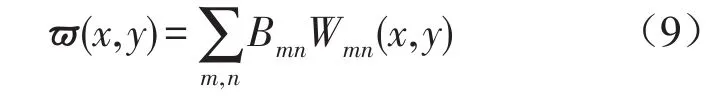
将式（9）代入（7），令p--p+=0，得到夹层板的固有频率

其中δb=Dπ4/b2C，β=b/a，kf=2Df/D，Df为表层抗弯刚度，ρ=(2tρf+hρc)/H为夹层板密度，ρf、ρc分别为表层和芯层密度，t、h分别为表层和芯层的厚度，H为夹层板总厚度，a、b分别为夹层板的长与宽，(m,n)为基频阶次。

本征函数的正交条件

将式（5）、（6）和（9）代入（7），同时将式（7）两边乘以Wpq(x，y)，再对整个板面积分得

根据1、θ≠0,φ=0；2、θ=0,φ≠0；3、θ≠0，φ≠0，可求出Bmn的三组值。将Bmn其代入式（9），再将式（9）代入式（5）和（6）即可得p-和p+。

隔声量是平板阻止声波透射平板的一种固有属性

Πi是入射声功率，Πt是透射声功率，测量时把板简支于两个房间的开口处。

对于一个入射平面波，由入射侧空气速度v-=p-/(ρ0c)，入射声功率可定义为

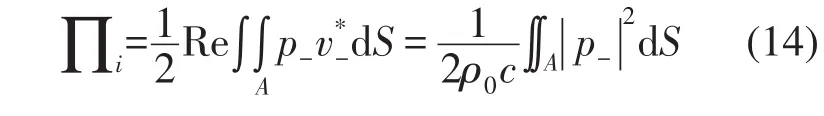
同理，透射声功率定义为

其中θlim=780是声场入射角的极限值[12]。

因此对于混响室隔声量为

2 夹层板的数值研究

2.1 夹层板数值模型

夹层板结构参数：上下表面采用钢板，长和宽都取0.25 m，面板、芯层厚度分别取4 mm、15 mm。面板材料特性：质量密度为7 850 kg/m3，弹性模量为2.1 e 5 Mpa，泊松比为0.287。芯层采用粘弹性丁基橡胶阻尼材料，材料特性为：质量密度为920 kg/m3，泊松比为0.49，选其在500 Hz时的弹性模量及损耗因子分别为4.57 Mpa和1.2。

声学计算时，声学单元尺寸与计算频率应满足：对于线性有限元和边界元模型，通常假设在最小波长内至少有6个单元，而对于二次单元最大单元的边长要求小于计算频率最短波长的1/3[13]。由于本文计算最高频率为6.3 kHz，根据fmax=c/6L(其中c=340m/s，L为单元的长度)，算得单元最大长度8.9 mm，实际声腔单元长度取8 mm。

本文数值模拟在两个房间（一个混响室，一个消声室）之间布置简支夹层板，计算其隔声量。结构网格在Patran中建立，声学网格在LMS Virtual.Lab11自带的Catia模块中建立；声学网格和结构网格通过接受面和辐射面一侧分别进行耦合；声学网格采用自动匹配层（AML）属性，一侧接收声源，另一侧辐射，如图2所示。

图2 夹层板的结构和声学模型

2.2 不同参数下夹层板的隔声量

2.2.1 不同损耗因子η下夹层板的隔声量

通过改变芯层的材料损耗因子η，研究其对夹层板隔声量的影响，取材料损耗因子η1=1.2,η2=0.12，其它参数不变。

图3是不同芯层材料损耗因子η下夹层板的隔声量曲线。从图3可知，在低频段芯层材料损耗因子的增加基本不影响夹层板的隔声量，而在中高频段影响却很显著。

图3 不同芯层材料损耗因子下夹层板的隔声量曲线

在0.1～1.25 kHz频率范围，两者的夹层板隔声量基本保持不变；在1.8～6.3 kHz频率范围，损耗因子η1=1.2的夹层板平均隔声量比损耗因子η2=0.12的高9.0 dB左右；而在1.25～1.8 kHz频率范围，损耗因子η2=0.12的夹层板平均隔声量比损耗因子η1=1.2的高2.4 dB左右。这是因为夹层板的响应由芯层控制，只改变芯层材料的损耗因子时，能量耗散主要因芯层的剪切变形产生，且芯层的损耗因子在一定的频率下有最大值，即先增大到达一定值后将逐渐减小。

2.2.2 不同芯层厚度h下夹层板的隔声量

通过改变芯层的厚度，研究其对夹层板隔声量的影响：芯层厚度分别取15 mm、10 mm、5 mm，其它参数不变。

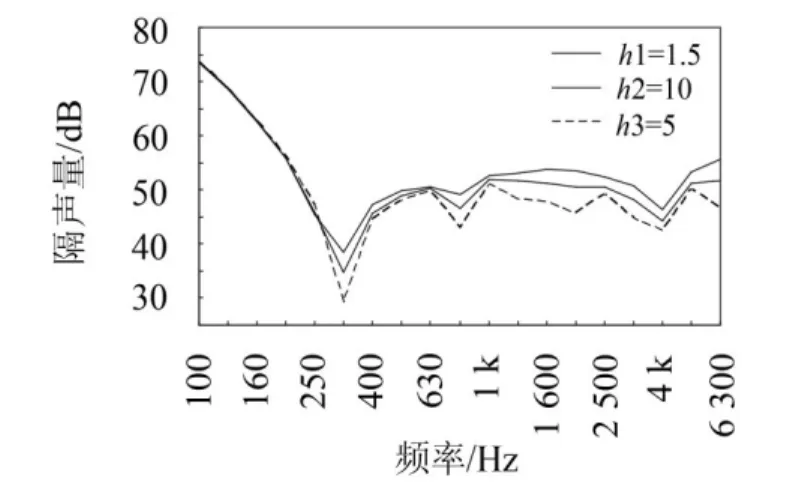
图4 不同芯层厚度下夹层板的隔声量曲线

图4是不同芯层厚度下的夹层板隔声量曲线，随着芯层厚度的增加，夹层板的隔声量增大，且三条曲线的变化趋势基本一致。在100～300 Hz频率范围，三者隔声量基本不变。而在0.3～6.3 kHz频率范围，当芯层h从5 mm增加到10 mm时，夹层板的平均隔声量增加2.7 dB左右；当芯层h从10 mm增加到15 mm时，平均隔声量增加2.1 dB左右。这是因为芯层厚度的增加，使面板远离中面，远离中心面的铺层在弯曲载荷将提供更大的贡献[14]，从而提高了夹层板抵抗弯曲变形的刚度，能量耗损能力增加。

2.2.3不同芯层弹性模量E下夹层板的隔声量

通过改变芯层的弹性模量，研究其对夹层板隔声量的影响，取弹性模量E1=0.457 Mpa、E2=4.57 Mpa、E3=45.7 Mpa，其它参数不变。

图5是不同芯层弹性模量下的夹层板隔声量曲线，当弹性模量分别为0.457 Mpa和4.57 Mpa时，在0.1～1 kHz频率范围两者的隔声量基本一致，而在1～6.3 kHz，弹性模量大的夹层板平均隔声量高5.2 dB左右。而当弹性模量从4.57 Mpa增加到45.7 Mpa时,在100～315 Hz频率范围，夹层板的平均隔声量增加了6.5 dB左右；在3.15～6.3 kHz频率范围夹层板的平均隔声量高出了8.75 dB左右；而在315～3 150 Hz频率范围夹层板平均隔声量基本一致。研究表明：当弹性模量增加，在中高频段，对夹层板隔声量影响显著；而在低频段，只有弹性模量增加到一定值才对夹层板的隔声量影响显著。

图5 不同芯层弹性模量下夹层板的隔声量曲线

2.2.4 不同平面尺寸下夹层板的隔声量

改变夹层板的平面尺寸，研究其对夹层板隔声量的影响，长宽尺寸分别取：0.5 m×0.5 m、0.25 m×0.25 m、0.125 m×0.125 m三种情况，芯层厚度h=5 mm，其它参数不变。

图6是不同平面尺寸下的夹层板隔声量曲线，当平面尺寸增加时，隔声量曲线的波谷密度增加。从式（10）可看出，当长宽比不变，且基频阶次（m，n）相同时，较大的b值对应的频率ωmn较小，即面内尺寸较大的夹层板具有更大的模态密度，从而由结构共振引起的隔声量波谷密度也将更大。这与文献[9]中描述的一致。低频段平面尺寸小的夹层板隔声性能好，而在中高频段夹层板的隔声量随着尺寸的增加有所提高。

3 结语

本文基于夹层板Hoff理论和声学机理，建立了夹层板的声振耦合理论模型，通过模态函数及其正交性求解了声振耦合系统方程。用数值方法对四边简支的橡胶夹层板进行了声学数值模拟，结果表明：芯层的材料损耗因子、材料弹性模量的增加对夹层板中高频段的隔声量影响明显；随着芯层厚度的增加，隔声量呈现增大的趋势；当平面尺寸增加时，隔声量曲线的波谷密度增加。

[1]张少辉，陈花玲，梁天锡.纤维增强树脂基复合材料阻尼特性的数值模拟[J].航空材料学报，2004，24(3)：10-14.

[2]张少辉，陈花玲.共固化复合材料粘弹阻尼结构的损耗因子研究[J].航空材料学报，2005，25(1)：53-57.

[3]潘利剑，张博明，戴福洪.简谐激励下共固化复合材料粘弹阻尼结构的损耗因子研究[J].振动与冲击，2008，27(2)：57-60.

[4]中国科学院北京力学研究所固体力学研究室板壳组.夹层板的弯曲稳定和振动[M].北京：科学出版社，1977.

[5]Simon F,Pauzin S.Sound transmission loss model of orthotropicsandwich panels[C].Proceedingsof EURONOISE‘95,European conference on noise control,Lyon,France,1995.

[6]Lee C,Kondo K.Noise transmission loss of sandwich plates with viscoelastic core[C].AIAA,Proceedings of structural dynamics and materials conference and exhibit,St.Louis,1999,40:2137-2147.

[7]Samir Assaf.Numerical prediction of noise transmission loss through viscoelastically damped sandwich plates[J].Journal of Sandwich Structures and Materials,2008:359-384.

[8]丁晓，王昌田，等.泡沫铝复合板低频吸声性能实验分析与研究[J].噪声与振动控制，2010，30(5)：196-198.

[9]何祚镛.结构振动与声辐射[M].哈尔滨：哈尔滨工程大学出版社，2001：82-85.

[10]任树伟，辛锋先，卢天建.蜂窝层芯夹层板结构振动与传声特性研究[J].力学学报，2013，45(3)：349-358.

[11]胡海昌.各向同性夹层板反对称小挠度的若干问题[J].力学学报，1963，6(1)：53-60.

[12]何琳，朱海潮，邱小军，等.声学理论与工程应用[M].北京：科学出版社，2006.

[13]李增刚，詹福良.声学仿真计算高级应用实例[M].北京：国防工业出版社，2010.

[14]王兴业，肖加余，唐羽章，等.复合材料力学分析与设计[M].长沙：国防科技大学出版社，1999.