拉索非线性随机振动的最优有界半连续控制

张巍，应祖光，胡荣春

（1.浙江理工大学经济管理学院实验中心，杭州 310018；2.浙江大学航空航天学院力学系，杭州 310027）

拉索是斜拉桥、大跨度索支撑结构等的重要构件[1]，但因抗弯和抗压刚度低而易于受环境激励产生大幅振动，需要进行振动控制研究。拉索确定性振动的主动和半主动控制已有一定研究[2―5]。然而，环境激励如风力、基础运动等通常具有随机性，斜拉索随机振动的最优控制研究相对缺乏[6]。而且，拉索随机振动的不确定性可能导致很大幅度运动，但实际主动和半主动控制器的控制力大小都有一定限制[7]，因此无法产生相应大的反馈控制力，从而退化按无界设计的控制效果，考虑控制力有界性的斜拉索非线性随机振动的最优控制研究尚有待于发展。

随机动态规划原理是确定系统非线性随机振动最优控制的一个基本理论，它将最优控制设计转化为求解动态规划(HJB)方程，应用变分原理可确定有界约束的最优控制[8]。bang-bang控制是一个常用的有界控制，但因系统响应的随机性而导致相应控制的不连续性，将产生受控系统的颤振，严重退化控制效果[9]。本文建立受控斜拉索的横向非线性运动方程，运用伽辽金法推导多模态耦合的振动方程；然后考虑系统激励的随机性与控制力的有界性，先后应用随机平均法、动态规划方法与变分法确定最优有界半连续控制律；最后通过数值结果说明控制效果。

1 受控斜拉索的非线性振动方程

考虑张紧的弹性斜拉索[5]，在铅直平面内横向激励与控制力作用下，其横向运动方程为[1]

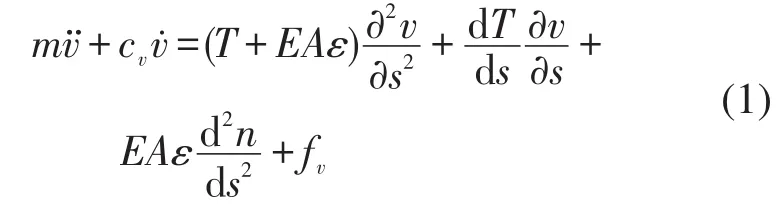
式中v是横向位移，s是曲线坐标，m是单位长度质量，cv是阻尼系数，T是静张力，EA是拉伸刚度，e是非线性动应变[4]，n是单位法向矢量，fv包含横向激励和控制力。设索两端固定，则边界条件为s=0，L(索长)时，v=0。利用非线性应变与张力表达式、静平衡关系，并作无量纲化，式(1)成为

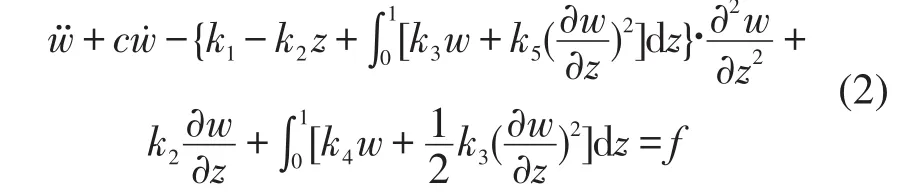
相应边界条件为z=0，1时，w=0，其中无量纲位移w=v/L，坐标z=s/L，斜拉索的倾斜角为a，水平静张力为Tx，c=cv/m，f=fv/(mL)

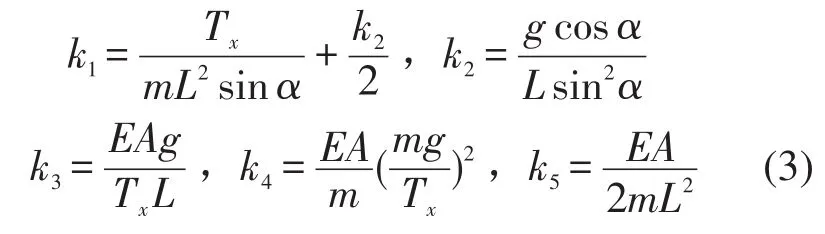
将无量纲位移展成

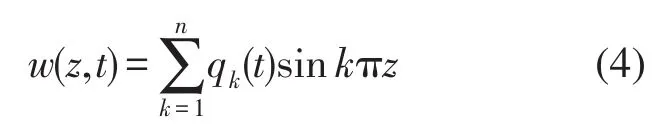
它满足索两端边界条件，其中qk为模态位移。考虑到索的模态振动幅值随模态阶次升高而迅速降低，保留到前3阶模态。将式(4)代入(2)，运用伽辽金法，可得索的模态振动方程

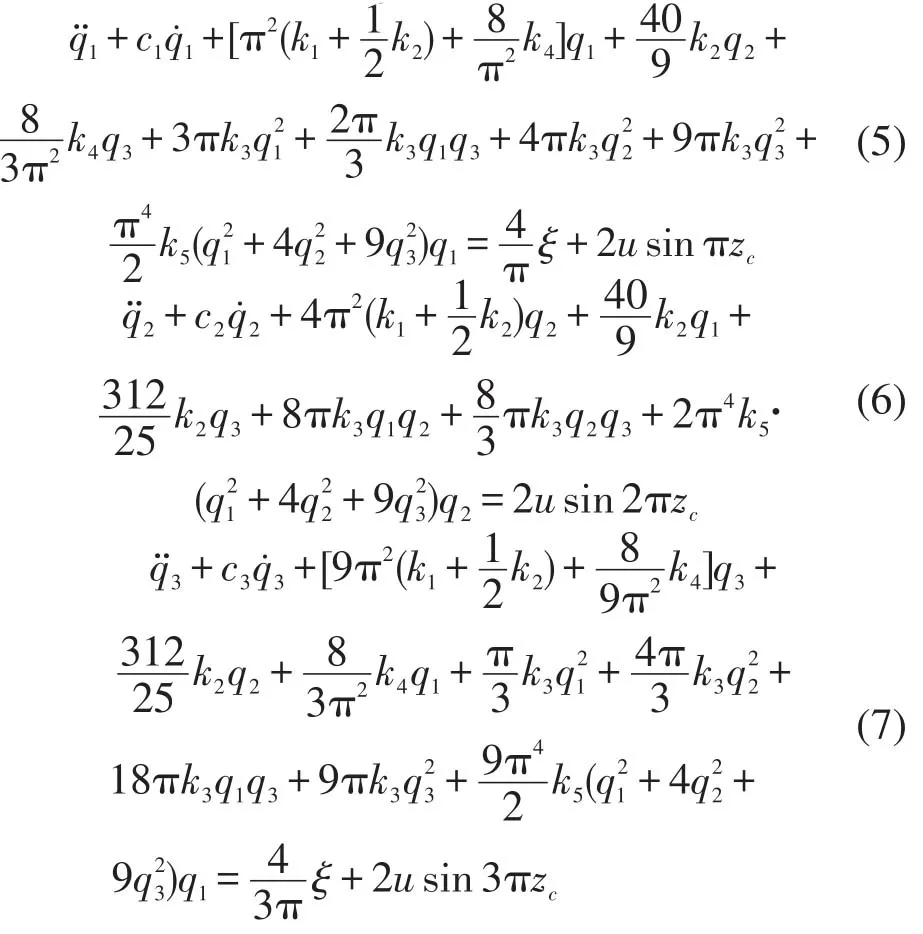
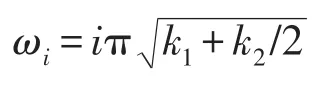
2 最优有界半连续控制力

将式(5)—(7)表示成Itô微分的状态方程

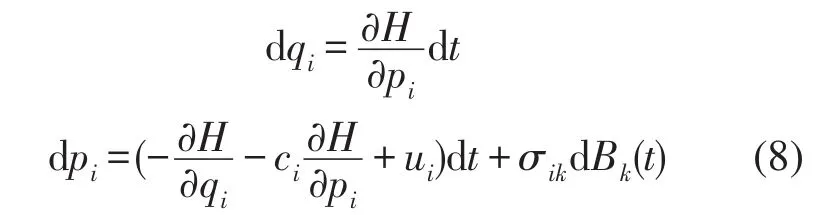
式中bi是正常数。应用随机平均法于式(8)，得到平均系统方程

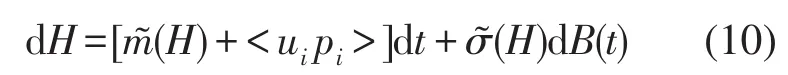
式中<·>是平均算符，是漂移系数，是扩散系数。系统(10)最优控制的性能指标表示为

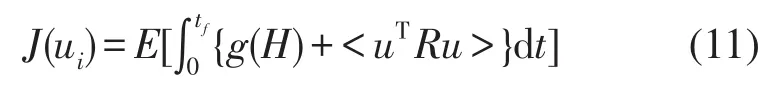
式中E[·]是期望算符，tf是控制的终时，R=diag[R1，R2，R3]，u=[u1，u2，u3]T，g(H)³0。根据随机动态规划原理，建立系统(10)和指标(11)的平稳HJB方程

式中l是H的函数。式(12)与(9)组成具有控制约束的动态规划问题，根据变分原理，可得最优控制律

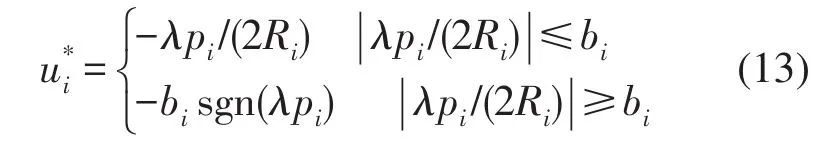
该控制具有界限bi，在界内具有连续函数形式，因此是一种有界半连续型的最优控制。其连续性优于非连续的bang-bang控制，从而可减轻非连续控制产生的颤振效应。将式(13)代入(12)求解之得到l，代回(13)即得非线性索系统的最优有界半连续控制。应用随机平均法可计算系统(8)控制前后的响应。

3 数值结果

考虑某受控斜拉索，具有参数L=130.0 m，a=0.984 rad，A=60.0 cm2，m=60.0 kg/m，zi=0.002，E=180 GPa，Tx=4 000 sina kN，D1=D2=D3=0.03，zc=0.9，bi=2.2，Ri=4.0 sinipzc，g=2H2。按照式(13)确定最优有界控制，计算受控索的均方位移，同时计算未控索的均方位移，得到相对降低值，并计算它与均方控制之比，用以说明控制效率。作为比较，给出bangbang控制均方位移的相对降低值，及其与均方控制之比。数值结果如图1、2所示，最优有界半连续控制的位移相对降低值随控制界限而提高(b=2.5时约为88%)，其值略小于bang-bang控制(b=2时两者之差约为0.02)，但差距随控制界限提高而缩小，其控制效率则高于bang-bang控制。图3、4展示的样本表明最优有界半连续控制力的连续性远优于bangbang控制力，从而能较大程度地减轻后者产生的颤振效应，改善实际控制效果。

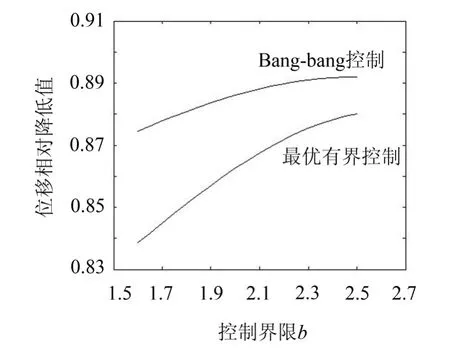
图1 均方位移的相对降低值(b=bi)

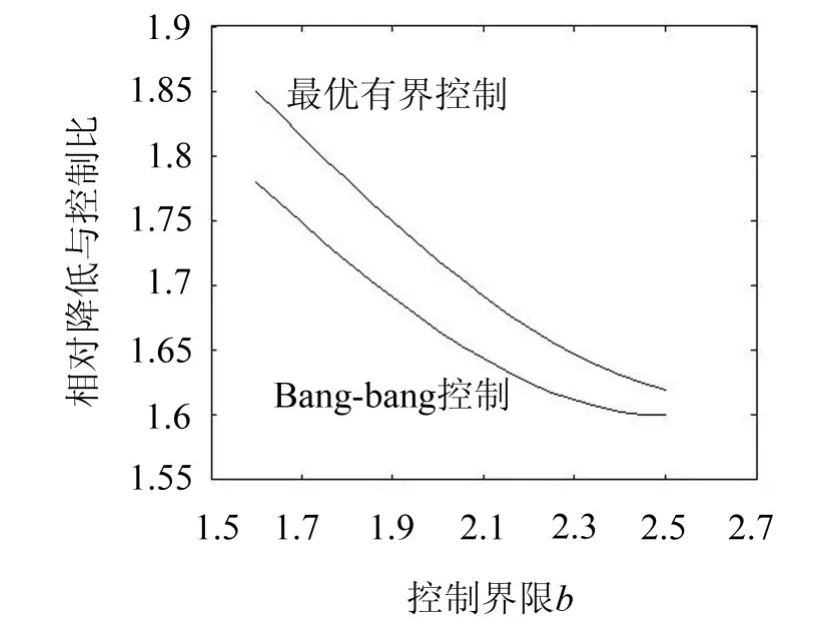
图2 位移相对降低值与控制力之比(b=bi)

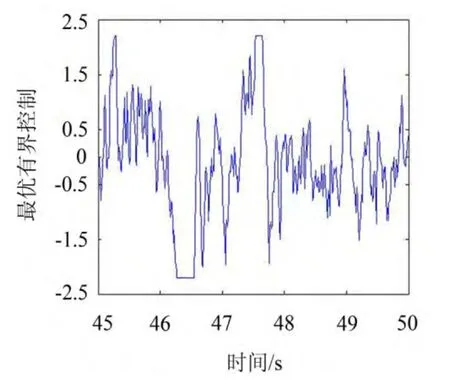
图3 最优有界控制力样本

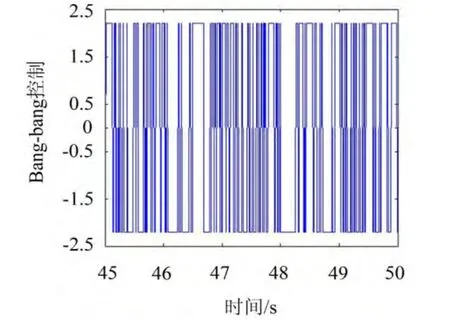
图4 Bang-bang控制力样本

4 结语

综合应用随机平均法、动态规划原理与变分原理研究了考虑控制力有界性的斜拉索非线性随机振动的最优控制问题。建立了受控斜拉索多模态耦合的横向非线性振动方程，应用随机平均法得到平均方程，应用动态规划方法建立HJB方程，应用变分法得到了非线性随机索系统的最优有界控制律。该非线性随机振动的最优有界半连续控制具有较高的效率与连续性，更切合实际控制器情况，数值结果表明能达到较好的实际控制效果。

[1]Irvine H M.Cable Structures[M].Cambridge:MIT Press,1981.

[2]Diouron T L,Fujino Y,Abe M.Control of wind-induced self-excited oscillations by transfer of internal energy to higher modes of vibration I:analysis in two degree of freedom[J].ASCE J.Eng.Mech.,2003,129:514-525.

[3]Zhou H J,Xu Y L.Wind-rain-induced vibration and control of stay cables in a cable-stayed bridge[J].Struct.Cont.HealthMoni.,2007,14:1013-1033.

[4]Ying Z G,Ni Y Q,Ko J M.Parametrically excited instability analysis of a semi-actively controlled cable[J].Eng.Struct.,2007,29:567-575.

[5]张巍，应祖光，王建文.风激拉索张弛振荡的最优控制分析[J].噪声与振动控制，2012，32(3)：21-24.

[6]Zhao M,Zhu W Q.Stochastic optimal semi-active control of stay cables by using magneto-rheological damper[J].J.Vib.Cont.,2011,17:1921-1929.

[7]Spencer B F,Dyke S J,et al.Phenomenological model for magneto-rheological dampers[J].ASCE J.Eng.Mech.,1997,123:230-238.

[8]Ying Z G,Ni Y Q,Ko J M.A bounded stochastic optimal semi-active control[J].J.Sound Vib.,2007,304:948-956.

[9]Chitour Y,Liu W,Sontag E.On the continuity and incremental-gain properties of certain saturated linear feedback loops[J].Int.J.Robust Nonlin.Cont.,1995,5:413-440.