轴流式人工心脏泵混合磁悬浮系统的耦合特性

李红伟，范友鹏，张云鹏，刘淑琴，关勇

（山东大学电气工程学院，山东济南 250061）

轴流式人工心脏泵混合磁悬浮系统的耦合特性

李红伟，范友鹏，张云鹏，刘淑琴，关勇

（山东大学电气工程学院，山东济南 250061）

植入式人工心脏泵要求体积小、质量轻、功耗低，为了满足这些要求，需要研究磁悬浮人工心脏泵的轴承特性。为此，对径向永磁轴承自身的耦合特性进行了理论分析与仿真，据此提出了心脏泵转子的磁悬浮支承方案，该方案采用两个径向永磁轴承和一个轴向电磁轴承来实现转子的五自由度稳定悬浮。根据径向永磁轴承的磁场分布特性，提出了采用两个关于转子轴线对称布置的霍尔传感器，从转子径向方向检测转子轴向位移的方法，理论分析揭示了转子径向位移和轴向位移在检测结果中的耦合关系，并给出了解耦方法，得出了轴向位移。基于研究成果设计了轴流式磁悬浮人工心脏泵原型机，并成功实现了转子的五自由度稳定悬浮。

人工心脏泵;电磁轴承;永磁轴承;位移检测;耦合

0 引言

磁悬浮人工心脏泵采用磁力轴承支承转子，消除了机械接触和摩擦，显著降低了对血液的破坏作用，受到了医学界和学术界的广泛关注［1－2］。

磁力轴承分为电磁轴承、永磁轴承和混合磁力轴承。植入式人工心脏泵通常采用便携式电池供电，要求体积小、质量轻、功耗低，因此不宜采用全电磁轴承来支承其转子。永磁轴承利用永磁力实现转子的被动稳定悬浮，无需控制系统，无功耗，结构简单，在人工心脏泵中得到了广泛应用［3－9］。但是永磁轴承无法同时实现转子的五自由度（即除转子沿自身轴线的转动自由度之外的其它五个运动自由度）静态稳定悬浮［10］。为了实现心脏泵转子的五自由度稳定悬浮，并显著降低系统的功耗、质量及控制复杂度，采用径向永磁轴承和轴向电磁轴承相结合的转子支承系统不失为一种理想的方案［11］。

径向永磁轴承无需控制系统，只需进行优化设计和轻量化设计。而轴向电磁轴承除了机械部件（电磁铁）外，还包括一套控制系统［12］，因此，需要进行优化的内容较多，其中之一就是传感器的选型。相比于常用的电涡流传感器和电感传感器，霍尔传感器具有质量更轻、体积更小的优点，更好的契合了人工心脏泵的要求，受到了学者们的青睐［11，13］。但是文献［11］额外增加了一个被测转子磁环来检测转子的轴向位移，增加了系统的质量和体积，文献［13］是利用霍尔传感器来检测转子的径向位移。而人工心脏泵采用径向永磁轴承时，可直接利用霍尔传感器来检测转子磁环的运动导致的空间磁场的变化，来反映转子的轴向位移。

根据恩休（Earnshaw）定理［10］，径向永磁轴承的径向刚度和轴向刚度、径向永磁力和轴向永磁力是相互耦合的，这给磁悬浮系统的结构设计以及控制系统的设计与调试带来了一定的难度。并且径向永磁轴承的转子磁环的径向运动和轴向运动都会改变空间磁场的分布，导致霍尔传感器的输出中耦合了转子的径向位移和轴向位移，必须进行解耦才能检测出转子的轴向位移。只有解决好这些问题，才能设计出性能优良的适用于植入式人工心脏泵的转子磁悬浮支承系统。

为此，在分析径向永磁轴承和轴向电磁轴承的特性以及两者之间的耦合关系的基础上，提出了一种适用于植入式人工心脏泵的磁悬浮支承系统方案，并从理论方面研究了转子磁环的径向位移和轴向位移在霍尔传感器检测结果中的耦合关系，以及解耦方法，为轴流式人工心脏泵混合磁悬浮系统的设计奠定理论基础。

1 轴流式磁悬浮人工心脏泵原理

轴流式磁悬浮人工心脏泵由前导叶、叶轮转子、后导叶、电动机、磁悬浮轴承系统和外壳等组成，如图1所示。

叶轮转子由轴向电磁轴承吸力盘、径向永磁轴承转子磁环、电动机转子磁环、叶轮等组成，由永磁直流无刷电动机驱动，带动血液在泵体内沿轴向流动，产生所需的血压和流量，满足人体需求。

图1 轴流式磁悬浮人工心脏泵结构示意图Fig.1The sketch of axial-flow maglev blood pump

2 径向永磁轴承耦合特性

2.1 力的耦合分析

磁悬浮人工心脏泵采用的径向永磁轴承由定子磁环和转子磁环两部分组成［14］，如图2所示，通常情况下，定转子磁环的宽度相同。

图2 径向永磁轴承结构示意图Fig.2The sketch of radial permanent magnetic bearing

忽略重力的影响，当转子磁环与定子磁环的中心轴线共线时，转子磁环受到的径向永磁合力为零;当转子磁环在径向方向偏离中心位置且位移为r时，转子磁环受到一个实际方向与径向位移r方向相反的径向永磁合力Fpr（图2中Fpr与r的正方向相同），使转子磁环回到其径向平衡位置，实现转子磁环的径向被动稳定悬浮。

当定、转子磁环在轴向方向重合时，转子磁环受到的轴向永磁合力为零;当定、转子磁环间有一个轴向小位移z时，转子磁环将受到一个实际方向与位移z方向相同的轴向永磁合力Fpz的作用，而越来越偏离其轴向平衡位置，无法稳定悬浮。

因此，当转子磁环的径向位移r和轴向位移z同时存在时，径向永磁合力Fpr和轴向永磁合力Fpz同时存在。

对某一径向永磁轴承，采用有限元法分析了转子磁环沿定子磁环中心轴线移动时，轴向永磁合力Fpz与轴向位移z之间的关系，如图3所示。

由图3可见Fpz是关于z的奇函数，当z=0时，Fpz=0;当z＞0时，Fpz随着z的增大先增大到最大值，再减小到零，然后反向增大。

图3 径向永磁轴承轴向力与转子轴向位移间的关系Fig.3The relationship between the axial force and the rotor axial displacement in radial permanent magnetic bearing

人工心脏泵转子的轴向运动范围比较小，一般不超过1 mm，由图3可知，当转子在轴向平衡位置（z=0）处的小范围内运动时，Fpz与z近似成线性关系，即

其中，Kpz为径向永磁轴承的轴向刚度，N/m。

2.2 刚度的耦合分析

径向永磁轴承的轴向刚度Kpz和径向刚度Kpr分别定义为

根据恩休定理，Kpz与Kpr之间的关系为

根据式（3）可知，径向永磁轴承的径向刚度和轴向刚度是相互耦合的，并且轴向刚度是径向刚度的2倍。根据图3及式（2）和式（3）可得径向永磁轴承的轴向刚度和径向刚度，如图4所示。需要说明的是由于分析的永磁力为轴承内部作用力，因此图4中的刚度符号与通常的刚度符号是相反的，但是这并不影响研究结果。

由图4可知，Kpz和Kpr是关于轴向位移z的偶函数。当|z|＜zT时，Kpz＞0，轴向不稳定，而Kpr＜0，径向稳定，轴承为径向永磁轴承;当|z|＞zT时，Kpz＜0，轴向稳定，而Kpr＞0，径向不稳定，轴承变为轴向永磁轴承。当|z|≤zL时，轴承刚度近似不变，为常数;当zL≤|z|≤zT时，轴承刚度随着z的增大而减小。z=zT是永磁轴承由径向轴承变为轴向轴承的转折点，因此，相同结构的永磁轴承的使用条件不同，其作用也不同。

图4 径向永磁轴承刚度与转子轴向位移之间的关系Fig.4The relationship between the stiffness of radial permanent magnetic bearing and the rotor axial displacement

2.3 耦合的利用

转子的轴向稳定悬浮通常需要两个相对布置的轴向电磁轴承来实现。而利用径向永磁轴承自身的耦合特性，自行设计了如图5所示的轴向仅采用一个轴向电磁轴承的磁悬浮支承方案，显著降低了系统的体积、质量和功耗。图5中，s0和z0分别为转子悬浮于平衡位置时轴向电磁轴承的气隙和径向永磁轴承定转子磁环间的相对轴向距离。

图5 人工心脏泵磁力轴承系统结构示意图Fig.5The sketch of magnetic bearing system in blood pump

该方案中，2个径向永磁轴承实现转子在径向4个自由度的悬浮，轴向悬浮由径向永磁轴承和轴向电磁轴承来共同控制。当转子在轴向方向由平衡位置处向A端运动时，轴向电磁轴承增大电磁力使转子回到平衡位置;当转子向B端运动时，轴向电磁轴承减小电磁力，径向永磁轴承的轴向永磁力使转子回到平衡位置。

当转子紧靠电磁轴承定子时，电磁力为零，永磁轴承必须提供足够的轴向永磁力使转子回到平衡位置，因此必须保证z0＞s0，但是z0不能过大，否则轴向电磁轴承需要提供的电磁力过大，从而增加系统的体积、质量、功耗和设计难度。

3 轴向轴承与径向轴承间的耦合

在图5所示的磁悬浮系统中，转子的轴向运动由轴向轴承的电磁力和径向轴承的轴向永磁力共同控制，这导致了径向轴承与轴向轴承间的力耦合和刚度耦合，增加了系统的结构设计难度和控制难度。

3.1 轴向电磁轴承特性

典型的轴向电磁轴承结构由定子铁心、线圈和转子吸力盘等组成，如图6所示，其电磁力为［12］

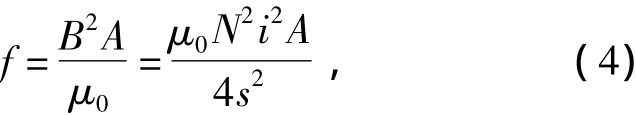
其中:A为中间铁心的横截面积，m2;μ0为真空磁导率，4π×10－7N/A2;N为线圈匝数;i为线圈电流，A; s为轴承气隙，m。

图6 轴向电磁轴承结构示意图Fig.6The sketch of axial electromagnetic bearing

为了简化控制，需要将式（4）在转子的平衡位置（i=i0，s=s0）处线性化为［12］

其中:ix=i－i0为控制电流，A;x=s－s0为转子位移，m;i0为偏置电流，A;s0为转子在平衡位置处的电磁轴承气隙，m;f（i0，s0）为静态工作点处的电磁力，N;为力－电流系数，N/A;kx=力－位移系数，N/m。

3.2 力的耦合分析

在人工心脏泵正常工作时，转子在轴向同时受到轴向电磁轴承的吸力Fe，血液轴向压力Fb以及径向轴承的轴向永磁力FpzA和FpzB的共同作用，如图7所示，其中Fe和Fb的方向与血液流动方向相反，FpzA和FpzB的方向与血液流动方向相同。

图7 转子轴向受力分析图Fig.7Axial mechanical equilibrium analysis of rotor

要使转子在轴向稳定悬浮，则有

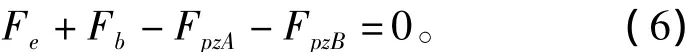
心脏泵转子的位移为小位移，将式（1）带入式（6），得

其中，z为转子质心的轴向位移，根据图5可知，|z|≤s0。z=0时，转子处于轴向平衡位置。

由式（7）可知，转子轴向位移z的变化引起轴向永磁力的变化，从而导致轴向电磁力的变化。在人工心脏泵转子启动时，电磁轴承需要提供的电磁力最大，并满足如下关系

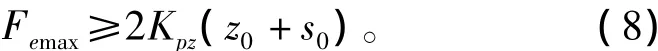
径向永磁轴承和轴向电磁轴承间的力耦合还体现在系统结构设计过程中。在设计结构时，希望电磁轴承所提供的电磁力越小越好，以降低系统质量和功耗，因此要求径向永磁轴承具有较小的轴向刚度Kpz;但是心脏泵工作时，又希望轴承具有较高的承载力和刚度，以减小转子的振动，提高抗干扰能力，因此要求径向永磁轴承具有较大的径向刚度Kpr。而Kpz和Kpr是相互耦合的，所以说，这两个要求是相互矛盾的。因此，径向永磁轴承的刚度耦合导致了系统结构设计中的矛盾，需要根据实际情况进行优化设计，尽量兼顾转子悬浮性能和系统对质量、体积及功耗的要求。

3.3 刚度的耦合分析

磁悬浮人工心脏泵正常工作时，根据图7可得转子的轴向运动方程为

将式（1）和式（5）带入式（9）中，整理后得到

其特征方程式为

根据式（11）绘制出转子轴向运动的控制框图，如图8所示。图中，Gc（s）为电磁轴承控制器传递函数;ka为功率放大器增益，A/V;ks为位移传感器增益，V/m。

图8 转子轴向运动的控制框图Fig.8Control diagram of rotor axial motion

可得轴向电磁轴承的等效闭环刚度［15］为

其中，Re［Gc（s）］为控制器传递函数的实部。

由式（13）可知，径向永磁轴承与轴向电磁轴承的刚度相耦合，加大了电磁轴承的负刚度，降低了电磁轴承对转子轴向运动的控制能力，也增加了电磁轴承控制器的设计和调试难度。因此，在电磁轴承控制器设计和系统调试时，必须考虑径向永磁轴承的轴向刚度。

其传递函数为

4 转子轴向位移检测中的耦合

为了契合人工心脏泵对体积和质量的要求，采用霍尔传感器，通过检测径向轴承转子磁环运动所导致的空间磁场分布的变化，来反映转子的轴向位移。但是转子的径向运动也会引起空间磁场分布的变化，而影响轴向位移检测结果，因此，必须研究转子径向位移和轴向位移与霍尔传感器输出电压之间的关系，建立数学模型，并进行解耦，以便准确检测出转子的轴向位移。

4.1 霍尔传感器的工作原理

霍尔传感器是基于霍尔效应工作的。如图9所示，半导体薄片置于磁感应强度为B的磁场中，磁场方向垂直于薄片，当有电流I流过薄片时，在垂直于电流和磁场的方向上将产生电动势，这种现象称为霍尔效应，该电动势称为霍尔电势，该半导体薄片称为霍尔元件。电流I越大、磁场强度B越强，霍尔电势就越高;磁场方向相反，霍尔电势的方向也随之改变，因此霍尔传感器能用于测量静态磁场或交变磁场。

图9 霍尔效应原理图Fig.9Principle of Hall effect

霍尔电势可表示为［16］

其中:UH为霍尔电势，V;kH为霍尔元件的灵敏度，与元件材料的性质与几何尺寸有关，Ω/T;I为控制电流，A;B为磁感应强度，T。

4.2 心脏泵转子轴向位移检测方法

如图10所示，当心脏泵转子仅仅沿轴向z运动时，霍尔传感器处的磁场发生变化，其输出电压也随之变化，从而将转子的轴向位移信号z转换为霍尔传感器的输出电压信号U，达到了检测转子轴向位移的目的。

图10 霍尔传感器检测转子轴向位移原理图Fig.10Principle of rotor axial displacement detection using Hall sensor

当霍尔传感器的控制电流I不变时，其输出电压U与垂直于其检测面的磁感应强度B成正比，即

其中，kB=kHI为系数，V/T。

心脏泵转子的位移为小位移，则磁感应强度B与轴向位移z之间的关系可在（z=0）处线性化为

其中:B0为z=0时霍尔传感器处的磁感应强度，T; kBz为系数，T/m。

将式（16）带入式（15），得到霍尔传感器输出电压U与转子轴向位移z之间的关系为

其中:U0=kBB0为z=0时霍尔传感器的输出电压，V;ks=kBkBz为霍尔传感器的增益，V/m。

4.3 转子轴向位移检测结果中的耦合

式（17）是在心脏泵转子仅仅沿轴向运动时分析得来的。但是心脏泵转子在正常工作时既有轴向运动又有径向运动，而径向运动同样会改变霍尔传感器处的磁场和霍尔传感器的输出电压，导致检测结果中，转子径向位移和轴向位移的耦合，无法获得准确的转子轴向位移。

设转子悬浮于平衡位置时，转子的径向位移x=0，轴向位移z=0。霍尔传感器检测的磁感应强度B是转子径向位移x和轴向位移z的函数，即

将式（18）在转子平衡位置（x=0，z=0）处线性化为

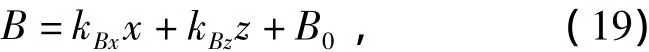
式中:kBx和kBz为系数，T/m;B0为（x=0，z=0）时霍尔传感器处的磁感应强度，T。

但是，kBx随着位移z的变化而变化，kBz也随着位移x的变化而变化，如式（20）所示。由于转子的位移为小位移，因此可以认为kBx不随x的变化而变化，kBz不随z的变化而变化。

其中:cx和cz为系数，T/m2;kBx0和kBz0为常数，T/m。

将式（19）和式（20）代入式（15）中，可得霍尔传感器的输出电压U与位移x和z之间的关系为

其中:ksxz=kB（cx+cz）为耦合增益，V/m2;ksx=kBkBx0为径向增益，V/m;ksz=kBkBz0为轴向增益，V/m。

由式（21）可知，图10所示的转子轴向位移检测方法中，转子的径向位移x和轴向位移z在检测结果中相耦合，共同影响霍尔传感器的输出电压。

4.4 位移解耦方法

若要利用霍尔传感器来检测心脏泵转子的轴向位移，必须对检测结果中的径向位移与轴向位移进行解耦。为此，采用如图11所示的方案，在转子轴线两侧对称布置两个相同的霍尔传感器A和B。

当转子既有径向位移x又有轴向位移z时，两个霍尔传感器的输出电压分别为

对2个传感器的输出电压求平均，可得

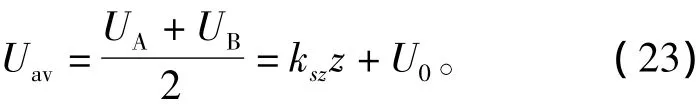
由式（23）可知，两个霍尔传感器的输出电压的平均值Uav仅与转子轴向位移z有关，与径向位移x无关，消除了转子径向位移对轴向位移检测结果的影响。

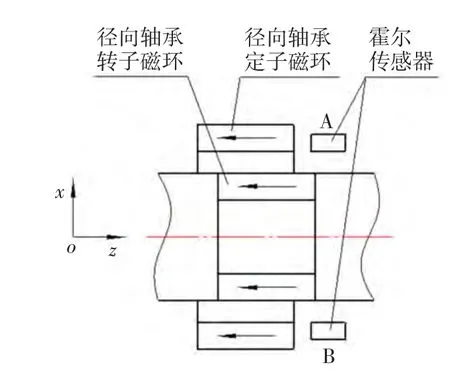
图11 位移解耦原理图Fig.11Decoupling principle of displacements

需要指出的是，本文在分析转子轴向位移检测方法中的耦合特性及解耦方法时，均以转子位移为小位移这一条件为基础，对相关参数进行了线性化，忽略了高阶项，因此，严格意义上来说，式（23）只是在最大程度上消除了转子径向位移对轴向位移检测的影响，并未彻底消除，所以，转子的径向位移还是会轻微的影响轴向位移的检测结果。后续将对该问题进行深入探讨，研究其中的非线性特性以及径向位移对轴向位移检测结果的影响程度。

5 实验

基于人工心脏泵磁悬浮系统耦合特性的研究，自行设计并加工了一台轴流式磁悬浮人工心脏泵原型机，如图12所示，采用两个径向永磁轴承和一个轴向电磁轴承来支承转子，以及对称布置的霍尔传感器来检测转子轴向位移，利用模拟PID控制器和线性功率放大器，实现了转子的五自由度稳定悬浮。转子轴向受到冲击干扰后能够快速恢复稳定悬浮，控制精度较高，如图13所示。

图12 轴流式磁悬浮人工心脏泵原型机Fig.12Prototype of axial-flow maglev blood pump

图13 转子轴向冲击干扰响应曲线Fig.13Impulse response of the rotor

6 结论

针对轴流式人工心脏泵的磁悬浮系统的耦合特性的研究得出以下结论:

1）径向永磁轴承自身存在力耦合和刚度耦合，利用这种耦合特性设计出的采用两个径向永磁轴承和一个轴向电磁轴承的磁悬浮系统是可行的，并能降低系统体积、质量和功耗;

2）采用对称安装在转子径向方向上的两个霍尔传感器来检测人工心脏泵转子的轴向位移时，对两个霍尔传感器的输出电压求平均值，可以最大程度的消除转子径向位移对轴向位移检测结果的影响。

混合式磁悬浮系统的耦合研究为轴流式磁悬浮人工心脏泵的研制奠定了理论基础，具有重要的理论和工程意义。

［1］姜华，席光.心脏泵的研究进展［J］.医疗卫生装备，2006，27（8）:33－35.

JIANG Hua，XI Guang.Development of blood pump［J］.Chinese Medical Equipment Journal，2006，27（8）:33－35.

［2］HOSHI H，SHINSHI T，TAKATANI S.Third-generation blood pumps with mechanical noncontact magnetic bearings［J］.Artificial Organs，2006，30（5）:324－338.

［3］ANTAKI J，PADEN B，BURGREEN G，et al.Blood pump having a magnetically suspended rotor:US，6447266B2［P］.2002－09.

［4］GOLDOWSKY M.Magnetic suspension blood pump:US，6527699B1［P］.2003－03.

［5］HUBER C，TOZZI P，HURNI M，et al.No drive line，no seal，no bearing and no wear:magnetics for impeller suspension and low assessment in a new VAD［J］.Interactive Cardiovascular and Thoracic Surgery，2004（3）:336－340.

［6］JARVIK R.Axial force null position magnetic bearing and rotary blood pumps which use them:US，6227820［P］.2001－05.

［7］NOH M，ANTAKI J，RICCI M，et al.Magnetic design for the pediaflow ventricular assist device［J］.Artificial Organs，2007，32 （2）:127－135.

［8］QIAN Kunxi，ZENG Pei，RU Weimin，et al.New concepts and new design of permanent maglev rotary artificial heart blood pumps［J］.Medical Engineering＆Physics，2006，28:383－388.

［9］GUAN Yong，LIU Shuqin，LI Hongwei，et al.Study on magnetic bearings system in axial-flow blood pump［C］//2010 International Conference on Mechanic Automation and Control Engineering （MACE2010），June 26－28，2010，Wuhan，China.2010: 3903－3907.

［10］EARNSHAW S.On the nature of the molecular forces which regulate the constitution of the luminiferous ether［J］.Trans Camb Phil Soc，1839，7（Part 1）:97－112.

［11］YANG Shengming，HUANG Mingshi.Design and implementation of a magnetically levitated single-axis controlled axial blood pump［J］.IEEE Transactions on Industrial Electronics，2009，56（6）:2213－2219.

［12］SCWEITER G，BLEULER H，TRAXLER A.Active magnetic bearing-basic，properties and application of active magnetic bearing［M］.Zurich:ETH，1994:31－67.

［13］钱坤喜，万福凯，茹伟民，等.永磁磁浮叶轮在心脏泵内的偏心距及振幅测量［J］.机械工程学报，2005，41（1）:181－183.

QIAN Kunxi，WAN Fukai，RU Weimin，et al.Position detection of permanent maglev impeller in centrifugal heart pump［J］.Chinese Journal of Mechanical Engineering，2005，41（1）:181－183.

［14］YONNET J P.Permanent magnet bearings and coulpings［J］.IEEE Transactions on Magnetics，1981，MAG－17（1）:1169－1173.

［15］赵雷，丛华，赵鸿宾.可控磁悬浮轴承刚度与阻尼特性研究［J］.清华大学学报:自然科学版，1999，39（4）:96－99.

ZHAO Lei，CONG Hua，ZHAO Hongbin.Study on stiffness and damping characteristic of active magnetic bearing［J］.J Tsinghua Univ:Sci＆Tech，1999，39（4）:96－99.

［16］陈文芗，洪兆祥.采用反馈随动机构扩大霍尔传感器位移测量范围［J］.仪器仪表学报，2001，22（3）:303－305.

CHEN Wenxiang，HONG Zhaoxiang.Using feedback servo mechanism to scale-up the measurement range on the shift by hore sensor［J］.Chinese Journal of Scientific Instrument，2001，22 （3）:303－305.

（编辑：张诗阁）

Coupling in hybrid magnetic levitation system of axial-flow blood pump

LI Hong-wei，FAN You-peng，ZHANG Yun-peng，LIU Shu-qin，GUAN Yong
（School of Electrical Engineering，Shandong University，Jinan 250061，China）

The implanted artificial blood pump requires small volume，light weight，low power dissipation and so on.To meet these requirements，the force coupling and stiffness coupling of the radial permanent magnetic bearing are studied by theory analysis and simulation.Basing the force coupling characteristics，a scheme of hybrid magnetic levitation system for the axial-flow maglev blood pump was presented.This scheme employed two radial permanent magnetic bearings and only one axial active magnetic bearing to levitate the blood pump rotor in five degrees of freedom.Then，the rotor axial displacement detection method was studied.This method used two Hall sensors，which were arranged symmetrically about the pump rotor axis and in the rotor radial direction，to detect the magnet field variation caused by the movement of rotor ring of the radial magnetic bearing.But the rotor radial displacements and axial displacement were all included in the outputs of the two Hall sensors.Therefore it analyzed the coupling relationship between the radial displacement and the axial displacement in the outputs of sensors.Then the decoupling method was studied and presented.According to the theory study results，a prototype of the axial-flow maglev blood pump was designed and manufactured.The rotor of the prototype is stably and successfully levitated in five degrees of freedom.

blood pump;active magnetic bearings;permanent magnetic bearings;displacement measurement;coupling

TH 133.3;R 318.11

A

1007－449X（2014）05－0105－07

2013－04－03

国家自然科学基金（51075236，51105231）

李红伟（1979—），男，博士，讲师，研究方向为磁力轴承理论与应用;

范友鹏（1984—），男，博士研究生，研究方向为磁力轴承控制及功放技术;

张云鹏（1982—），男，博士，讲师，研究方向为永磁轴承技术;

刘淑琴（1958—），女，博士，教授，博士生导师，研究方向为磁力轴承技术、风力发电技术;

关勇（1973—），男，博士，副教授，研究方向为磁力轴承理论与应用。

刘淑琴