蜂窝网络中能效最大的最优中继位置研究

2014-02-23李云，朱雪，廖超

重庆邮电大学学报(自然科学版) 2014年1期

李云，朱雪，廖超

(重庆邮电大学移动通信技术重庆市重点实验室，重庆 400065)

0 引言

近些年，随着移动通信市场的迅速发展，用户对通信速率的需求日益增长，由此带来的能耗问题变得十分严峻。因此，综合考虑用户速率和能耗问题，提高用户传输能效具有非常重要的实际意义。在一个小区覆盖范围内，由于路径损耗等因素，数据传输速率会随着用户与基站距离的增加而降低，因此，小区边缘用户的数据速率变得很低。为了扩大覆盖范围和提高系统容量，一些通信标准，如 IEEE802.16j［1］和 3GPP LTE－A 引入了中继的概念。在上行传输中，用户不直接将信号发送给基站，而是先发送给一个中继，然后再由该中继把信号转发给基站。一方面，中继可以有效地扩大覆盖范围;另一方面，网络中合理地部署中继，可以使用户把数据传输到相比于基站更近的目的地［2］，从而降低路径损耗，提高数据传输速率。除此之外，相比于基站，固定中继具有一些明显的优势:低复杂度、低建造、低维护成本以及低能耗等。

中继部署问题在不同的应用场景中引起了普遍关注，比如无线传感器网络［3］，蜂窝网络［4］，802.16j WiMAX 网络［5］和无线体域网［6］等。有少数研究人员对中继的最优位置做了深入研究。文献［7］在单小区内考虑上行传输，以系统容量最大化为目标，运用矢量量化方法，研究了中继优化部署问题。文献［8］以覆盖范围最大化为目标，分别在单小区和多小区的网络模型下，研究了中继优化部署问题。其中，在单小区内，依据节点正确解码概率来界定覆盖范围。在多小区内，考虑小区间干扰因素，提出了一种迭代算法。文献［9］在多个候选位置、多个中继、多个基站的网络模型下，以最大化系统容量为目标，研究了基站和中继的部署问题以及用户和中继的最优功率分配问题。文献［10］以系统容量最大化为目标，研究了单小区内2种协作模式(放大转发和解码转发)下的中继优化部署问题。

如上所述，目前关于中继位置的研究工作主要集中在提高容量和扩大覆盖范围方面，几乎没有以最大化能效为目标的中继部署的研究工作。随着蜂窝网络中能耗的增大，只考虑提高容量而忽视能耗问题是不充足的，提高能效具有重要意义。本文在单小区内考虑上行传输，研究以能效最大化为目标的最优中继位置问题。首先，本文定义了上行传输能效(uplink energy efficiency，uEE)为平均用户上行传输容量与平均上行发射功率的比值。其中，上行发射功率包括用户和中继的发射功率。然后，推导出用户均匀分布下，无中继网络和中继网络的uEE解析表达式。分析和仿真结果表明，在给定其他网络参数，比如小区半径、中继数目等条件下，能够通过优化中继位置获得最大能效。并且，通过与文献［7］的对比，表明本文提出的方法能够有效提高上行传输能效。

1 网络模型

网络模型如图1所示，设小区半径为R，基站位于小区中心，坐标为(0，0)，Nr个固定中继环绕基站呈对称分布，把小区等分为Nr个扇区，每个固定中继与基站的距离均为bR，其中，b∈(0，1］。小区内用户(总数为|UT|，用集合UT表示)均匀分布。本文考虑上行传输，假设为2层网络。用户传输数据到与其最近的中继(即所在扇区的中继)，然后由此中继把用户数据转发给基站，用户与基站之间不存在直传链路。此外，本文假设小区内没有频率复用，即用户和中继不允许同时在相同的频带上传输数据，因此，不同的用户和中继之间互不干扰。利用正交频分多址(orthogonal frequency division multiple access，OFDMA)技术，中继可以同时为多用户提供服务。与文献［7］类似，本文假设中继到基站的无线链路容量足够大，中继有能力同时转发本扇区所有用户的数据。

图1 网络模型Fig.1 Network model

为了简化信道模型，本文忽略阴影衰落、小尺度衰落等其他衰落，仅考虑路径损耗。假设信道增益G0=d－∂，其中，d表示用户与为其提供服务的中继之间的距离或是用户与基站之间的距离，∂表示路径损耗指数。一般情况下，∂∈［2，5］。由此，根据香农定理得到单位带宽下用户获得的容量为

(1)式中:Pu表示用户发射功率;N0表示噪声功率。当N0和∂为定值时，用户获得的容量由用户发射功率和用户与中继之间的距离(或用户与基站之间的距离)决定。表1中列出了其他一些参数的定义。

表1 参数定义Tab.1 Parameter definition

2 上行传输能效分析

本文的主要研究目标是优化中继位置以获得最大的uEE。这一节通过分析得到uEE的解析表达式。

2.1 平均用户上行传输容量

定义C表示中继网络的平均用户上行传输容量。小区内用户均匀分布，因此，不同扇区内的平均用户上行传输容量相等。接下来计算由第1个固定中继(the first fixed relay station，FRS1)服务的扇区内的平均用户上行传输容量(即全网平均用户上行传输容量)，设 FRS1的坐标为(bR，0)，根据(1)式和(2)式，得到平均用户上行传输容量的解析表达式为

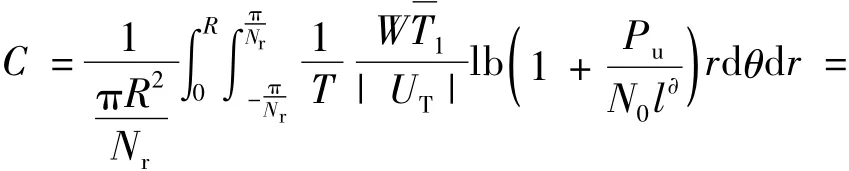
2.2 平均上行发射功率

平均上行发射功率P定义为所有用户和中继的发射功率的总和在所有用户上的平均值。在第1节中，假设中继有能力同时转发本扇区所有用户的数据。满足这一前提条件，得到每个中继到基站链路的最小容量为

2.3 上行传输能效

根据(4)式和(8)式，中继网络中的uEE的解析表达式为

根据(5)式，无中继网络中的上行传输能效(uEE0)的解析表达式为

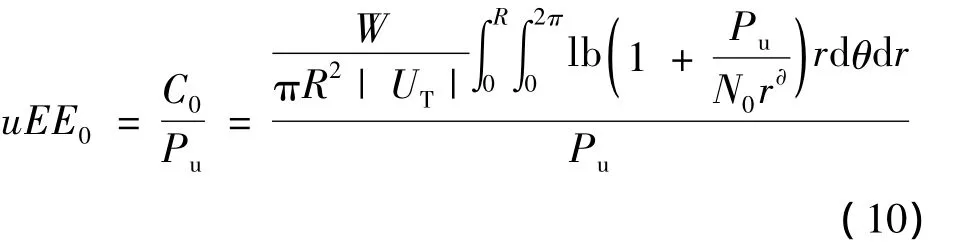
从(9)式可以看出，当 Pu，Nr，ω，W，R，|UT|，∂，N0这些参数取定值时，uEE是参数b的函数，参数b决定着中继的位置。第3节将评估b对uEE的影响。

3 性能评估

通过分析和仿真的方法，评估b对uEE的影响。仿真工具采用MATLAB。分析结果由(9)式通过数值计算方法得到。在仿真中，在小区内随机放置用户，所有的仿真结果为100个随机拓扑的平均值。

3.1 上行传输能效(uEE)和b的关系

图2描述了uEE和b的关系，给定参数W=20 MHz，|UT|=200，∂=4，Pu=0.5 W，N0= －90 dBm，R=2 500 m，ω =0.5，Nr=4，从图2可以看出，b的取值(即中继的位置)对uEE的影响非常大。存在一个最优的b值能够使得中继网络获得最大uEE。此外，分析结果与仿真结果的相对误差小于4%，验证了第2节分析的正确性。

图2 上行传输能效(uEE)vs.bFig.2 Uplink energy efficiency(uEE)vs.b

3.2 不同参数对uEE和最优b值的影响

评估不同参数(小区半径、中继数目、用户占用的资源比例)对uEE以及最优b值的影响。首先，根据(9)式得到参数的不同取值对应的不同最优b值，以及对uEE的影响。并且，本文的方法(energyefficiency optimization relays’positions，EORP)将和无中继网络(non－relay network，NRN)以及文献［7］进行性能对比，其中，EORP方法取得的是对应不同最优b值的最大uEE。为了对比EORP和NRN的上行传输能效，本文定义能效增益G=uEE/uEE0，本文中G保留2位小数。

3.2.1 上行传输能效(uEE)和小区半径R的关系

表2 最优b值，G vs.小区半径RTab.2 Optimal values of b，G vs.cell radius R

给定 W=20 MHz，|UT|=200，∂ =4，Pu=0.5W，N0=－90 dBm，ω=0.5，Nr=4。表2列出了不同小区半径 R对应的不同最优 b值。图3描述了EORP，NRN以及文献［7］3种情况下的uEE。从表2可以看出，当R增大时，为了获得最大上行传输能效，最优b值逐渐减小，即中继逐渐靠近基站。并且，增益G随着R的增大而增大。这是由于当R增大时，用户与基站的平均距离增大，导致平均路径损耗增大，说明在较大的小区中部署中继更具优势。从图3可以看出，EORP的uEE均高于NRN和文献［7］的uEE。当 R＜1 250 m时，文献［7］的 uEE低于NRN的uEE，表明文献［7］以高能耗为代价获取最大上行传输容量，很显然这是不完善的。

图3 上行传输能效(uEE)vs.RFig.3 Uplink energy efficiency(uEE)vs.cell radius R

3.2.2 上行传输能效(uEE)和中继数目Nr的关系

给定 W=20 MHz，|UT|=200，∂ =4，Pu=0.5W，N0= －90 dBm，R=2 500 m，ω =0.5。表 3列出了不同中继数目Nr对应的不同最优b值。图4描述了EORP，NRN以及文献［7］3种情况下的uEE。从表3可以看出，当Nr增大时，最优b值逐渐减小，以获得最大上行传输能效，此时，中继逐渐靠近基站。增益G随着Nr的增大而逐渐增大，但是，当Nr＞14时，继续增加中继数目并不能提高网络性能。同样，从图4可以看出，对于EORP存在一个最优Nr值使得网络取得最大uEE。EORP的uEE均高于NRN和文献［7］的uEE。此外，文献［7］只有2≤Nr＜6的结论，本文只绘出了对应条件的曲线。

表3 最优b值，G vs.中继数目N rTab.3 Optimal values of b，G vs.relays’number N r

图4 上行传输能效(uEE)vs.N rFig.4 Uplink energy efficiency(uEE)vs.relays’number N r

3.2.3 上行传输能效(uEE)和用户占用的资源比例ω的关系

给定参数 W=20 MHz，|UT|=200，∂ =4，Pu=0.5W，N0= －90 dBm，R=2 500 m，Nr=4。表4列出了不同用户占用的资源比例ω对应的不同最优b值。图5描述了EORP，NRN以及文献［7］3种情况下的uEE。从表4可以看出，当ω增大时，中继逐渐靠近基站(最优b值逐渐减小)，以获得最大上行传输能效。当ω=0.7，G=1.87，此时，网络有最大uEE。从图5可以看出，ω对uEE的影响非常大。对于文献［7］，当ω＜0.34或是ω＞0.61时，uEE小于NRN的uEE。并且随着ω的逐渐增大，uEE快速下降，此时，中继分配的资源较少，为了能够成功转发所有用户数据，需大幅度提高发射功率，导致总能耗大幅提高(例如，当ω=0.7时，Pr=79W)，而在实际网络中，中继并不能达到如此高的发射功率。在EORP方法中，对于ω的所有取值，中继的发射功率不超过2 W。总体来讲，当资源分配合理时，EORP相比NRN和文献［7］能够有效提高uEE。

表4 最优b值，G vs.用户占用的资源比例ωTab.4 Optimal values of b，G vs.ratio of resources which are assigned to users

图5 上行传输能效(uEE)vs.用户占用的资源比例ωFig.5 Uplink energy efficiency(uEE)vs.ratio of resources which are assigned to users

在本小节中，对于不同的参数，给出了EORP方法的分析值和仿真值，两者相对误差均不超过4%，再次表明本文分析的正确性。

4 结束语

本文在蜂窝网络中研究了单小区内，以能效最大为优化目标的中继位置问题。定义了uEE，并给出了用户均匀分布下无中继网络和中继网络的uEE解析表达式。分析和仿真结果表明，可以通过优化中继位置获得最大uEE。最后，评估了不同的参数如小区半径、中继数目和用户占用的资源比例对最优中继位置以及最大uEE的影响。此外，通过和无中继网络和文献［7］的方法对比，表明本文提出的方法能够有效提高上行传输能效。

［1］LIN Bin，HO PH，XIE Liangliang，et al.Optimal Relay Station Placement in IEEE 802.16j Networks［C］//ACM.In Proceedings of 2007 ACM International Conference on Wireless Communications and Mobile Computing.New York，NY，USA:ACM conference publications，2007:25－30.

［2］HAN Congzheng，HARROLD T，ARMOUR S，et al.Green radio:radio techniques to enable energy－efficient wireless networks［J］.IEEE Communications Magazine，2011，49(6):46－54.

［3］MISRA S，SEUNG D H，XUE Guoliang，et al.Constrained relay node placement in wireless sensor networks to meet connectivity and survivability requirements［C］//IEEE.In Proceedings of the 27th IEEE INFOCOM.Phoenix， AZ:IEEE conference publications，2008:281－285.

［4］BULAKCIO，REDANA S，RAAF B，et al.Performance Enhancement in LTE－Advanced Relay Networks via Relay Site Planning［C］//In Proceedings of IEEE 71st Vehicular Technology Conference.Taipei，Taiwan:IEEE conference publications，2010:16－19.

［5］LU H C，LIAOWanjiun，LIN F Y.Relay station placement strategy in IEEE 802.16j WiMAX networks ［J］IEEE Transactions on Communications，2011，59(1):151－158.

［6］徐文燕，张祖凡.基于中继协作的无线体域网能效性能分析［J］.重庆邮电大学学报:自然科学版，2012，24(5):620－624.

XUWenyan，ZHANG Zufan.Performance analysis of energy efficiency of relay cooperation in wireless body area network［J］.Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition，2012，24(5):620－624.

［7］POURAHMADIV，FASHANDIS，SALEH A，etal.Relay Placement in Wireless Networks:A Study of the Underlying Tradeoffs［J］.IEEE Transactions on Wireless Communications，2011，10(5):1383－1388.

［8］JOSHIG，KARANDIKAR A.Optimal Relay Placement for Cellular Coverage Extension［C］//IEEE.In Proceedings of2011 IEEENCC.Bangalore:IEEE conference publications，2011:1－5.

［9］ISLAM M H，DZIONG Z，SOHRABY K，et al.Capacity－Optimal Relay and Base Station Placement in Wireless Networks［C］//IEEE.In Proceedings of 2012 IEEE ICOIN.Bali:IEEE conference publications，2012:358－363.

［10］DONG Yu，ZHANG Yong，SONG Mei，et al.Optimal Relay Location in OFDMA Based Cooperative Networks［C］//IEEE.The 5thInternational Conference on IEEE Wireless Communications，Networking and Mobile Computing.Beijing，China:IEEE conference publications，2009:1－4.