论代数体函数的唯一性

李海英

（吕梁学院汾阳师范分校，山西 汾阳 032200）

论代数体函数的唯一性

李海英

（吕梁学院汾阳师范分校，山西 汾阳 032200）

文章围绕代数体函数唯一性开展，将代数体函数的加法及乘法定义，并且证明了运算后的结果仍是代数体函数．并且应用新定义的加法，将联系重值的唯一性定理推广到多值的代数体函数。

代数体函数；函数唯一性；数学定理

设集合C∈D内有如下一组无共同零点的解析函数，Av（z），Av－1（z），……，A0（z），在此函数中Av（z）≠0，那么二元复方程为

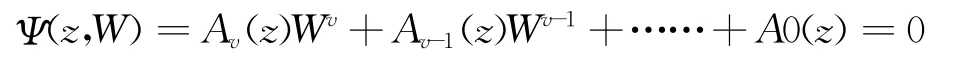
设定区域D中v值代数函数W（z），假如D＝｛｜z｜＜1｝，那么W（z）是｜z｜＜1内的v值代数体函数。若Ψ（z，W）不可以约W，那么v为W（z）不可约代数体函数［1］。

z0∈D是W（z）的临界点，只有在Av（z0）值为零或Ψ（z0，W）为零且偏导数Ψw（z0，W）为零存在有限或无限个根，临界点的所有集称成为临界集，可用Sw表示，其补集为正则集Tw＝D－Sw。任意临界点z0∈Sw均为孤立点，在z0周围｜（z－z0）vW（z）｜有界，这些都可以去奇点或极点，所以排列在球面上根据球距［2］。文中大部分是单独基于Tw上讨论，其余孤立点可直接由联系性唯一明确。

在此关系内，v值为代数体函数W＝W（z）中单值定义域是连续的曲面Tw，这一区域内的点均为正则函数元素［3］。也可以将其记做。所有W（z）的两个正则函数元素均存在路径γ⊂Tw可使二者相互解析。

Nevanlinna针对v值代数体函数W（z）问题中作出了平均中值函数和a值点三项定义：密指量、特征函数、级

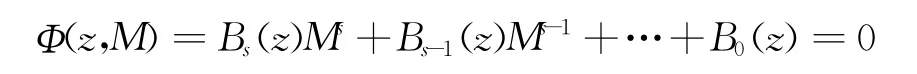
其中s值为代数体函数，涉及到的Bs（z），Bs－1（z），……，B0（z）为区域D中不存在公共零点的函数。

定理A v值代数体函数W（z）与s值代数体函数M（z）相加是Vs值代数体函数（W＋M）（z）。

引理1 设W值代数体函数W（z）为v值代数体函数，M（z）是s值代数体函数，且W（0）和M（0）中均不含极点，则

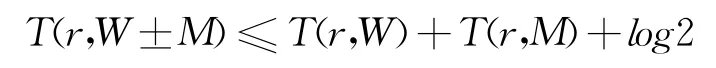
复平面中涉及到的代数体函数唯一性目前以获得良好结果［4］。但就角域内两个代数体行数所共享共值唯一性问题方面的研究数量尚且不足，文中围绕这一问题展开论述，为了叙述的顺利开展，先就有关定义和记号作出解释。

基于此Δ（θ）表示W（z）有关b的ρ级聚线。

一、定理1结果与证明

1、定理1 设W（z），M（z）为复平面上的v值和s值代数体函数，aj（j＝1，……，2v＋2s＋1）为2v＋2s＋1个判定的复数，若Ω（α，β）内存在）＝，M（z））且射线Δ（θ）（α＜θ＜β）为W（z）或M（z）对于某复数的ρ（ρ＞π／（β－α））级聚线，那么W（z）≡M（z）。

2、证明

二、定理2结果与证明

1、定理2

分别设W（z），M（z）均为复平面上的v值，s值代数体函数，aj（j＝1，……，q）是q＝2v＋2s＋1＋［2v／k］个判定复数，这一表达式中，v，s，k为正整数且s≤v。若中存在关系等式k）（aj，W（z））＝那么射线Δ（θ）（α＜θ＜β）为W（z）或M（z）有关复数的ρ（ρ＞π／（β－α））级聚线，那么W（z）≡M（z）。

2 证明

假设M（z），W（z）分别对应单位圆｜z｜＜1中的s值和v值为代数体，aj（j＝1，……，2v＋2s＋1）数量是2v＋2s＋1个判定复数。如果W（z）或M（z）的级为σ（0＜σ＜∞），且在单元圆内存在关系等式＝，那么W（z）≡ M（z）［6］。

证明 可以设aj（j＝1，……，2v＋2s＋1）均是有限复数，否则，只要变换一个就可以。

［1］李华仙·代数体函数微分多项式的值分布［J］．纯粹数学与应用数学，2013（3）：318－324．

［2］李华仙，高凌云·代数体函数微分单项式的值分布［J］．暨南大学学报：自然科学与医学版，2013（3）：249－252．

［3］王钥，高凌云·关于两类复非线性微分方程的代数体函数解［J］．系统科学与数学，2013（2）：246－254．

［4］何一农·关于代数体函数涉及重值的奇异方向［J］．南阳师范学院学报，2012（3）：1－5．

［5］王松敏·代数体函数与其系数函数的增长级关系Ⅱ［J］．．数学物理学报：A辑，2011（6）：1647－1653．

［6］张洪申·单位圆内代数体函数涉及重值的奇异点［J］．南阳师范学院学报，2011（12）：1－4．

［7］柴富杰，巫伟亮·代数体函数的公共值的唯一性定理［J］．嘉应学院学报，2011（5）：25－27．

［8］向士东，孙道椿，王松敏·关于代数体函数的注记［J］．华南师范大学学报：自然科学版，2010（4）：5－8．

Uniqueness of Algebroid Functions

Li Haiying
（Luliang University，Fenyang 032200，Shanxi，China）

This article focuses on the uniqueness of algebroid functions of addition and multipication defined algebroid function and prove the results remain Algebroidal function．With a new definition of addition，Generalized uniqueness theorem will contact the weight value to multi valued algebroid functions．

Algebroidal Function；Function Uniqueness；mathematical theorem

王德红）

O174．53

A

1673－9507（2014）02－0124－03

2014－02－25

李海英 （1981．09～），女，吕梁学院汾阳师范分校教师。研究方向：函数。