水下爆炸两气泡相互作用的数值计算研究

李健，荣吉利，林贤坤，项大林

(1.广西科技大学 汽车与交通学院，广西 柳州545006;2.北京理工大学 宇航学院，北京100081;3.广西汽车零部件与整车技术重点实验室，广西 柳州545006)

0 引言

两气泡或多气泡融合现象在物理、化学、医学及工业生产中广泛存在并占据着重要的地位，如化学领域中的气体与液体、液体与液体之间的相互反应;医学领域中利用多气泡击碎结石现象;能源生产中利用沸腾使水变成蒸汽从而推动涡轮转动的过程等。整个气泡融合过程主要包括气泡间相互吸引而引起的运动、气泡壁间液体的挤压、失稳、射流形成及最终的融合等阶段。影响气泡的融合现象涉及的因素较多，主要有质量交换、气泡表面张力、范德华力、布朗运动等。致使气泡融合机理还没有被完全揭示，很多行为特点还难以预测，因此，研究两气泡或多气泡之间的相互作用能加深人们对这些领域中相关物理现象的理解，对许多工程应用也有着重要的意义，有必要对气泡运动、水射流、气泡融合问题进行深入的研究。

气泡融合问题可通过实验与仿真的方法进行研究，实验方法主要是利用气泡发生器在液体中产生大量气泡，通过相应的测试设备研究气泡运动与融合的行为规律［1］，此外也可利用水下爆炸这一简单而有效方法进行气泡融合力学特性的研究。数值仿真计算方面目前大都采用边界元或有限体积法［2-5］。多气泡数值计算方面，Chew 等［6］利用边界积分方法研究了近刚性壁面两气泡的运动特性，结合实验测试验证方法的正确性。Rungsiyaphornrat等［7］利用边界积分方法研究了水下爆炸相互融合问题。李章锐等［8］采用边界积分方法对水下三维气泡的动力学特性进行模拟，研究了浮力对气泡运动特性与射流形成之间的联系。王诗平等［9］通过自行研制的水中气泡发生装置，通过实验测试方法了解了两气泡相互作用过程中出现的融合、射流等现象，通过实验提出了气泡之间的无量纲距离、无量纲周期等参数来描述气泡耦合特性。

边界元方法只在边界离散，大大降低了计算成本，但是在射流产生、气泡破碎及环形气泡形成方面有一定的局限性，此方面目前研究成果较少，而采用有限元方法进行气泡特性的研究相对更少。为了对两气泡运动数值模拟研究提供有益的补充，本文对单个气泡在水下运动特性进行仿真分析，通过将气泡最大半径、脉动周期与经验公式的对比，验证有限元模型与计算方法的正确性，以此为基础，研究两气泡水平距离、垂直距离、初始角度等参数对气泡运动特性的影响规律。

1 理论分析

1.1 气泡初始条件

目前关于气泡初始状态求解的方法较多，主要包括Rayleigh 模型［10-11］和文献［12 -14］提出的气泡体积加速度模型，后者主要是分别建立了药包参数和流场压力以及气泡体积加速度与流场压力之间的关系，并利用压力等效关系最终确定气泡的初始半径与初始膨胀速度，其体积与体积膨胀速度的表达式如(1)式～(2)式所示:

式中:V为气泡体积;ρ为流体密度;Pc=;mc、ac分别为药包的药量和半径;K1、K2、A、B 为与炸药有关的材料参数。对于密度1 600 kg/m3的TNT 炸药，K1=52.1，K2=0.090，A = 0.18，B =0.185. 考虑r0=即可求出不同时刻气泡的初始半径及径向速度。

如图1 所示为1.0 kg 球形TNT 炸药在0 ～1.2 ms时间段内，气泡半径及径向速度的时程曲线。

图1 气泡半径及径向速度时间历程曲线Fig.1 Time-history curves of radius and velocity of bubble

炸药引爆后，压力瞬间增加，故初始时刻气泡径向速度变化率非常明显，之后的冲击波传播过程中气泡膨胀速度逐渐平缓。针对这一规律，由图1 可见，当t≥0.8 ms 时，气泡径向速度的变化已经很小了，即可认为此时初始气泡形成。本文，t 取0.8 ms时对应的气泡膨胀速度为174.5 m/s，初始半径为0.303 m.

1.2 气泡运动的经验公式

研究人员通过大量的实验获取足够的数据，结合理论推导、曲线拟合等得到了水下爆炸中冲击波压力、气泡压力、气泡半径及脉动周期等经验公式，为计算结果的准确性提供有力的参考。气泡脉动最大半径与周期的经验公式分别如(3)式和(4)式［14］所示:

式中:K 为与炸药性质有关的系数，对TNT 炸药，K取1.6;p0为周围水的静压力(kg/cm2);W 为气泡的装药量(kg);z0为气泡所处位置的流体静压的等效水深(m)。

2 数值模拟

2.1 有限元建模

本节首先建立流场区域的三维有限元模型，流场区域为15 m×15 m ×15 m，流场全部用六面体欧拉网格划分，单元数量为135×135×135=2 460 375 个，其中每个单元的几何尺寸相同，且每个方向上的长度均为0.111 m，约为气泡初始半径的1/3，能够满足计算精度的要求［15］。通过对MSC.DYTRAN 有限元软件的二次开发，实现流场初始与边界条件的定义，并将数值计算结果与经验公式对比，验证有限元模型与数值计算方法的正确性。

2.2 初始条件及边界条件定义

为在有限区域内真实反映流场特性，需定义流场的静水压力以及与之对应的边界条件。由于MSC. DYTRAN 有限元软件并不能通过直接定义重力加速度实现流场静水压力的定义。因此，需根据每个网格所处的位置，通过EXINIT 子程序将静水压力值逐一赋到对应的网格上。同样，为了能够在有限的计算区域真实模拟无限水域流场特点，即当流场边界两侧出现压力差时，流体会从高压区通过边界流向低压区，可利用EXFLOW2 子程序将不同的静水压力值赋到流场边界上，最终实现三维流场静水压力与边界条件的定义。

2.3 状态方程

文中忽略气泡运动对气体压力的影响，认为气体的压力仅和气泡的初始状态及其体积有关，即气泡内的压力p 与气泡体积V 的关系:

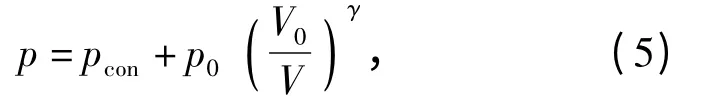
式中:pcon为可冷凝气体的饱和蒸汽压，量级与大气压相当，一般可忽略;p0和V0分别为气泡形成时的初始压力和初始体积;γ 为气体的比热比，对于TNT 水中爆炸的爆轰产物，γ 取1.25.

水的状态方程利用MSC.DYTRAN 软件中已有的多项式状态方程来描述，其形式为

式中:μ=(ρ/ρ0)-1;ρ0为材料参考密度;e 为比内能;对于水介质，取a1=2.134 ×109Pa，a2=6.561 ×109Pa，a3=1.126 ×1010Pa.

3 计算结果及讨论

3.1 单个气泡数值计算结果

对于单一气泡，计算工况为装药量为1.0 kg 的TNT 炸药在水下10 ～45 m 处爆炸，并将气泡脉动最大半径与周期与经验公式(3)式、(4)式进行对比，验证数值计算的正确性。如图2 所示，不同工况下气泡脉动半径的时间历程曲线。

图2 气泡脉动半径时间历程曲线Fig.2 Time-history curves of radius of bubbles detonated at different depth

由图2 可看出，气泡脉动的初始半径为0.303 m，随着爆心处水深的增加，气泡最大半径及与之对应的脉动周期也会逐渐减小。

如表1 所示，1 kg 球形TNT 炸药在10 ～45 m 等不同水深处运动，其最大半径与脉动周期与经验公式的对比。可看到，气泡脉动最大半径的仿真结果略大于经验公式，而脉动周期略小于经验公式结果，但从整体上而言，数值计算结果与经验公式吻合得较好，气泡最大半径的误差能够控制在8%以内，而脉动周期的误差能够控制在7%以内。通过与经验公式的对比分析，验证了水下爆炸气泡脉动模型建立和数值计算方法的正确性。

表1 不同工况下气泡脉动最大半径与周期仿真结果与经验公式的对比Tab.1 Comparison computational results and experimental results of the radius and period of bubble pulsation

3.2 两气泡数值计算结果

为研究两气泡水中相互作用的运动规律，以单一气泡数值计算模型为基础，建立水下爆炸两气泡脉动的数值计算模型，两气泡的状态方程完全相同。由于气泡坍塌、射流方向、射流速度等参数与爆心初始位置、气泡脉动周期、气泡最大半径等关键参数有密切关系，因此本节将研究距离参数、初始角度对气泡坍塌、射流角度、射流速度的影响。计算模型示意图如图3 所示。

图3 两气泡初始位置示意图Fig.3 Schemaic diagram of initial locations of two bubbles

当两气泡连线与水平线夹角α 为0°时，表示两气泡沿水平方向排列;当夹角α 为90°时，表示两气泡沿竖直方向排列;当两气不处于同一水平面时，相同条件下的气泡由于所处水深的不同会导致其最大半径和脉动周期的不同。为方便讨论，以两气泡连线中点处的参考气泡最大半径Rmax为特征长度，中点处静水压力pamb为特征压力，则特征时间为t =Rmax(ρ/pamb)1/2，速度的无量纲表达式为v/(Rmax/t)，两气泡中心初始位置之间的距离定义为d =2L/Rmax，即将参考气泡最大半径的2 倍作为特征长度，分别研究水平、垂直距离及夹角α 对气泡运动特性的影响规律。

3.2.1 水平距离对气泡运动特性的影响

如图4 所示为2 个装药量相同的TNT 炸药在相同水深且初始水平距离d =1.0 时其相互作用的演化过程。

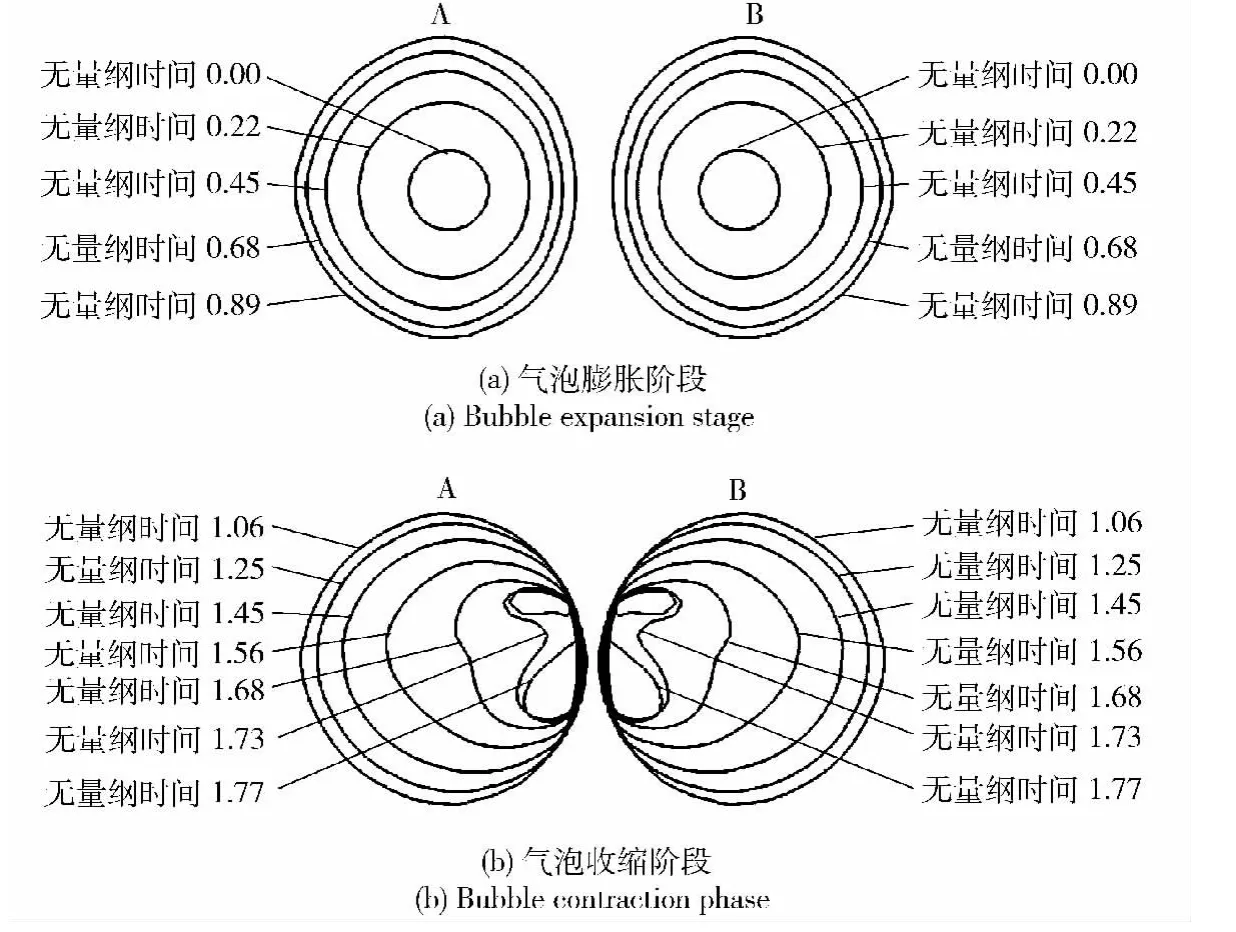
图4 水平距离d 为1.0 时两气泡运动演化过程Fig.4 Evolution processes of interaction of two bubbles for horizontal standoff distance d=1.0

由图4 可看出，当初始水平距离d 较小时，气泡之间的Bjerknes 力影响显著，明显强于浮力的影响，表现为坍塌发生于每个气泡的外侧，气泡A 形成由左下指向右上方向的射流，气泡B 产生右下指向左上方向的射流，最终两股射流均会击穿气泡并相互作用，而气泡也会由初始的球形变成环状气泡。

由于两气泡水平放置时其运动具有对称性，因此仅研究左侧气泡的运动特性。如图5 所示，描述的是左侧气泡射流角度、速度与气泡水平距离之间的关系。

图5 气泡水平排列时射流角度、速度和距离之间关系Fig.5 The relationship among angle and velocity of jet and horizontal distance

由图5 可看出，气泡射流角度会随着水平距离的增加而增加，而射流速度会随着水平距离的增加而减小。表现为当两气泡初始距离d 取1.0，即2 倍最大气泡半径时，气泡之间的Bjerknes 力影响显著，所形成射流的角度较小，约为7°左右，且射流速度也较大，其无量纲速度为5.25;随着气泡间水平距离的增加，其气泡射流与水平线的夹角随之增加，且增幅明显，表现为当两气泡初始距离d 取3.0，即6 倍最大气泡半径时，所形成射流角度已为76°，而当d 取4.0 时，射流角度约为86°，此时可认为气泡间的Bjerknes 力较弱，浮力占主导，在其作用下形成竖直向上的射流，且与之对应的射流速度相对较低，其无量纲量约为1.4.

3.2.2 垂直距离的影响

如图6 所示为两气泡在初始垂直距离d =1.0，即垂直距离为2 倍气泡最大半径时气泡脉动的演化过程。

由图6 可看出，当初始水平距离d 较小时，气泡之间的Bjerknes 力影响显著，明显强于浮力的影响，表现为气泡B 的坍塌发生于气泡的顶部，形成由竖直向下的射流;而气泡A 在Bjerknes 力浮力共同作用下，坍塌产生于气泡底部，形成竖直向上的射流，最终射流击穿气泡并相互作用，气泡也会由初始的球形变成环状气泡。

图6 竖直排列初始距离d 为1.0 时两气泡运动演化过程Fig.6 Evolution processes of interaction of two bubbles for vertical standoff distance d=1.0

由于两气泡沿垂直方向分布，因此其坍塌与射流方向均会沿竖直方向，为此，主要研究垂直距离对气泡射流速度的影响。如图7 所示，描述的是两气泡射流速度与垂直距离的变化规律。

图7 气泡竖直排列各气泡射流速度与距离之间的关系Fig.7 Relationship between jet velocity and vertical distance

由图7 可看出，随着两气泡垂直距离的增加，气泡之间的Bjerknes 力影响逐渐减弱，表现为上下气泡所产生的射流速度会随着垂直的距离的增加而减小，特别是上气泡。当垂直距离超过6 倍气泡最大半径(d=3.0)时，气泡顶部的运动速度已接近于气泡收缩时的速度，此时可认为上气泡顶部不会产生坍塌;而与之对应的下气泡，由于Bjerknes 力与浮力对气泡作用效果相同，导致下气泡底部发生坍塌并形成竖直向上的射流，因此，虽然随着初始距离的增加下气泡形成向上射流的速度会降低，但其射流速度会略高于上气泡顶部的射流速度。

3.2.3 初始角度的影响

与气泡竖直排列时类似，仍以两气泡连线中心点处气泡为参考，对两气泡各参数进行无量纲化。如图8 和图9 所示，分别为两气泡初始距离为d =1.0 时其最终射流角度和速度与两气泡初始夹角之间的关系曲线。

图8 d=1.0 时气泡A 射流角度、速度与初始角度之间关系Fig.8 Relationship among the velocity and angle of jet and the initial angle of bubble A for d=1.0

图9 d=1.0 时气泡B 射流角度、速度与初始角度之间关系Fig.9 Relationship among the velocity and angle of jet and initial angle of bubble B for d=1.0

由图8 和图9 可看出，由于初始距离较小，此刻Bjerknes 力影响显著，表现为气泡射流方向基本与原初始角度相同，而射流的速度变化不大且相对较高。由图5、图7 距离对射流速度影响规律可看出:气泡射流速度随着距离的增加降低明显，为此，当气泡初始距离d=3.0 时，气泡间距离相对较远，射流速度相对较低，此时主要考虑初始角度与射流角度之间的关系。

如图10 所示为气泡A 与气泡B 初始距离d =3.0 时，最终射流角度与气泡初始角度之间的关系曲线。

图10 d=3.0 时气泡射流角度与初始角度之间关系Fig.10 Relationship among the velocity and angle of jet and the initial angles of two bubbles for d=3.0

由图10 可看出，当初始距离增大时，气泡间的Bjerknes 力对气泡运动影响效果降低，浮力的影响逐渐显现。随着气泡连线与水平线夹角的增加，气泡A 最终射流的角度由42°逐渐增加至90°，气泡B最终射流角度由132°逐渐减小至90°，即随着两气泡连线与水平夹角的增加，两气泡坍塌所形成的射流方向会逐渐沿竖直方向移动。

4 结论

1)以气泡体积加速度模型作为气泡初始条件定义，结合自行开发的定义流场初始条件和边界条件的子程序，可较准确地计算出水下爆炸气泡脉动的全物理过程，且满足计算精度要求。

2)两气泡水平排列时，随着气泡间距离的增加，Bjerknes力影响效果逐渐减弱，浮力随之占主导，表现为随着气泡射流角度随着气泡间距离的增加而增大，而射流速度会随着水平距离的增加而减小。

3)两气泡竖直排列时，随着气泡间距离的增加，Bjerknes力影响效果逐渐减弱，气泡射流速度逐渐减小，上气泡会先后形成竖直向下射流、竖直向下与向上的对射流及竖直向上射流，而下气泡竖直向上的射流速度会逐渐减小。

4)两气泡初始时存在夹角时，随着距离的增加，两气泡最终的射流方向会逐渐向竖直方向移动，并最终与竖直方向重合，射流速度会随着距离的增加而减小。

References)

［1］金辉，张庆明，高春生，等.不同边界条件水下爆炸气泡脉动对比的试验研究［J］. 兵工学报，2009，12，30(增刊2):213-217.JIN Hui，ZHANG Qing-ming，GAO Chun-shen，et al. Comparison experimental study of underwater explosion bubble pulse among the different boundaries［J］. Acta Armamentarii，2009，12，30(S2):213 -217. (in Chinese)

［2］Klaseboer E，Manica R，Chan D Y C，et al. BEM simulations of potential flow with viscous effects as applied to a rising bubble［J］.Engineering Analysis with Boundary Elements，2011，35(3):489-494.

［3］S Shervani-Tabar M T，Seyed-Sadjadi M H，Shabgard M R.Numerical study on the splitting of a vapor bubble in the ultrasonic assisted EDM process with the curved tool and workpiece［J］.Ultrasonics，2013，53(1):203 -210.

［4］Menon S，Lal M. On the dynamics and instability of bubbles formed during underwater explosions［J］. Experimental thermal and fluid science，1998，16(4):305 -321.

［5］荣吉利，李健. 基于DYTRAN 软件的三维水下爆炸气泡运动研究［J］. 兵工学报，2008，29(3):331 -336.Rong Ji-li，LI Jian. Research on the motion of three-dimensional underwater explosion bubble with DYTRAN software ［J］. Acta Armamentarii，2008，29(3):331 -336. (in Chinese)

［6］Chew L W，Klaseboer E，Ohl S W，et al. Interaction of two oscillating bubbles near a rigid boundary［J］. Experimental Thermal and Fluid Science，2013，44:108 -113.

［7］Rungsiyaphornrat S，Klaseboer E，Khoo B C，et al. The merging of two gaseous bubbles with an application to underwater explosions［J］.Computers ＆ Fluids，2003，32(8):1049 -1074.

［8］李章锐，宗智，董婧，等. 两个气泡相互作用的某些动力特性研究［J］. 船舶力学，2012，16(7):717 -729 LI Zhang-rui，ZONG Zhi，DONG Jing，et al. Some dynamic characteristics of the interactions of two bubbles［J］. Journal of Ship Mechanics，2012，16(7):717 -729. (in Chinese)

［9］王诗平，张阿漫，刘云龙，等. 同相气泡耦合特性实验研究［J］.力学学报，2012，44(1):56 -64.WANG Shi-ping， ZHANG A-man， LIU Yun-long， et al.Experimental study on interaction of in phase bubbles［J］. Chinese Journal of Theoretical and Applied Mechanics，2012，44(1):56-64. (in Chinese)

［10］Rayleigh L. On the pressure developed in a liquid during the collapse of a spherical cavity［J］. The London，Edinburgh，and Dublin Philosophical Magazine and Journal of Science，1917，34(200):94 -98.

［11］Price R S. Similitude equations for explosives fired underwater，TR 80-299［R］. NSWC:Naval Surface War-fare Center，1979.

［12］Hunter K S. Global-shape-function models of an underwater explosion bubble［D］. Colorado:University of Colorado，2001.

［13］周霖，谢中元，陈勇. 炸药水下爆炸气泡脉动周期工程计算方法［J］. 兵工学报，2009，30(9):1202 -1205.ZHOU Lin，XIE Zhong-yuan，CHEN Yong. An engineering calculation method on the bubble pulse period of underwater explosion［J］. Acta Armamentarii，2009，30(9):1202 -1205.(in Chinese)

［14］库尔. 水下爆炸［M］. 北京:国防工业出版社，1960:135 -239.Cole. Underwater explosions［M］. Beijing:National Defense Industry Press，1960:135 -239. (in Chinese)

［15］李健，荣吉利，杨荣杰，等.水中爆炸冲击波传播与气泡脉动的实验及数值模拟［J］. 兵工学报，2008，29(12):1437 -1443.LI Jian，RONG Ji-li，YANG Rong-jie，et al. Experiment and numerical simulation of shock wave propagation and bubble impulse of underwater explosion［J］. Acta Armamentarii，2008，29(12):1437 -1443. (in Chinese)