基于MATLAB的风电机组故障间隔时间分布模型研究﹡

文 | 刘波，许洁，安宗文

基于MATLAB的风电机组故障间隔时间分布模型研究﹡

文 | 刘波，许洁，安宗文

随着全球风能快速发展，风电机组运行数量不断增加，影响风电机组稳定运行的各类故障不断出现，严重影响着风电机组的运行成本。因此，如何提高风电机组的运行可靠性日益受到人们的广泛关注。风电机组作为可修复系统，衡量其可靠性的重要指标之一就是故障间隔时间。故障间隔时间反映了产品的时间质量，是体现产品在规定的时间内保持其特有功能的一种能力，一般以小时为单位，通常也称为平均无故障工作时间。贾亚洲等利用故障间隔时间对不同对象的寿命分布模型进行描述，根据故障间隔时间的相对频率直方图和累计故障频率分布图，选取了相应的分布函数形式，并对其进行参数估计，最终确定了能较好拟合相应产品的故障间隔时间分布模型。

因此，本文以收集到的某风电场30台风电机组52个月的运行数据为基础，提取其故障间隔时间，根据故障间隔时间，绘制出风电机组的相对频率直方图和累积故障频率分布图。通过与常见寿命分布函数曲线进行比较，初步确定风电机组故障间隔时间的分布形式，并借助MATLAB软件对其进行参数估计、曲线拟合及假设检验。最终快速、准确的确定风电机组故障间隔时间的分布模型，为风电机组的设计、生产、使用和维修提供理论依据。

风电机组故障间隔时间

根据所收集到的某风电场30台风电机组52个月的运行数据，将每台风电机组每相邻两次发生故障的时间相减，看作是该机组这两次故障的间隔时间，即为该机组两次故障之间无故障工作的时间。通过这种方法即可依次获得该风电

图1 DJ16故障间隔时间分布示意图

机组52个月内的故障间隔时间。

以其中一台（DJ16）为例，根据设备台账记录的52个月内的运行数据，提取其故障间隔时间如下：

依照上述方式，依次将30台风电机组52个月内的故障间隔时间提取出来，共有321个故障间隔时间段。

故障间隔时间分布模型的初步判断

在整理数据，找出其规律性的过程中，最常用到的一种方法就是绘制其直方图。通过作直方图，可以求出一批数据（一个样本）的样本均值及样本标准差，更重要的是根据直方图的形状可以初步判断出该批数据总体属于哪种分布。因此，可以根据风电机组的故障间隔时间绘制它的直方图，通过直方图的形状对它的分布形式进行预知。其直方图的具体作图步骤如下：

（1）根据风电机组的故障间隔时间，找出其最大值L=14352h，最小值S=24h；

（2）将上述整理获得的321个故障间隔时间进行分组。一般用经验公式：式中：n为观测的故障个数，这里n=321。（3）计算组距Δt，即组与组之间的间隔：

（4）确定各组分点值，即各组的上限值和下限值以及各组的中值。

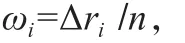
（6）作相对频率直方图：

以风电机组的故障间隔时间t为横坐标，相对频率fi为纵坐标，绘制相对频率直方图。将直方图中各直方的中点尽量连成一条光滑的曲线，即可得到概率密度函数的近似曲线，如图2所示，从中可以看出经验密度曲线呈现单调下降的趋势。

（7）作累积故障频率分布图

以风电机组的故障间隔时间t作为横坐标，累积频率为纵坐标，画出累积故障频率分布图，如图3所示。将分布图中的点尽量连成一条光滑的曲线，它表示总体的累积分布函数曲线，从图中可以看出累积故障分布函数呈外凸形。

故障间隔时间分布模型的拟合检验

在可靠性数据的分析中，常见的分布形式有指数分布、正态分布、对数正态分布、威布尔分布四类。由概率论可知，正态分布和对数正态分布的概率密度函数曲线呈单峰型，指数分布的概率密度函数曲线呈单调下降行，而威布尔分布的概率密度函数曲线根据其形状参数的不同或呈单峰或呈单调下降行。因此，通过风电机组故障间隔时间的相对频率直方图和累积故障频率分布图与常见分布函数曲线的比较，初步确定风电机组故障间隔时间的分布类型为：正态分布、对数正态分布或双参数威布尔分布。

一、正态分布

正态分布是机械产品中常见的分布，它适用于描述因腐蚀、磨损、疲劳而引起故障的产品寿命分布。

正态分布的分布函数为

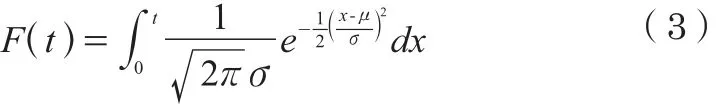
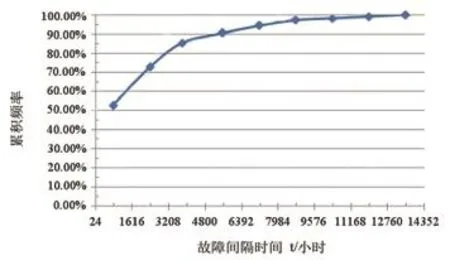
图3 风电机组故障间隔时间累积故障频率分布图

经标准化后为

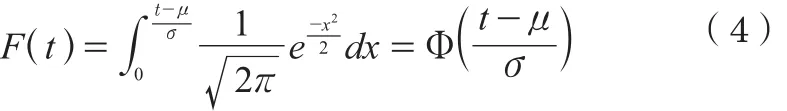
其参数μ和σ分别为均值和标准差。

（一）正态分布参数估计

正态分布在MATLAB软件中可运用函数normfit进行参数估计。该命令运用极大似然法给出了正态分布参数的点估计和区间估计。调用格式如下：

[muhat, sigmahat, muci, sigmaci]＝normfit(data, alpha)

则服从正态分布时，运用MATLAB命令对风电机组故障间隔时间分布函数参数的估计值为：

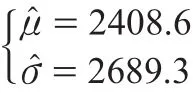
正态分布函数模型为

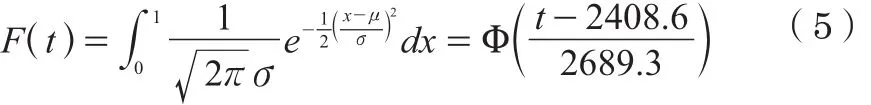
（二）正态分布拟合

在MATLAB软件中，利用函数normrnd根据函数normfit估计的参数值，抽取风电机组故障间隔时间服从正态分布时的随机数，调用函数normcdf求出对应的正态分布累积分布函数。利用MATLAB软件绘制出正态分布累积分布函数曲线，与风电机组实际的故障间隔时间累积分布曲线对比如下图4。

（三）正态分布假设检验

根据K－S检验法的基本思想，将样本观测值的累积频率Fn(x)与假设的理论频率分布Fx(x)相比较来建立统计量。在MATLAB中K－S检验的命令为kstest，它能有效实现假设分布函数的检验。其调用格式为

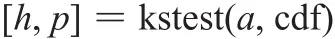
若h=0接收原假设；h=1拒绝原假设；p为原假设成立的概率；显著水平为0.05。

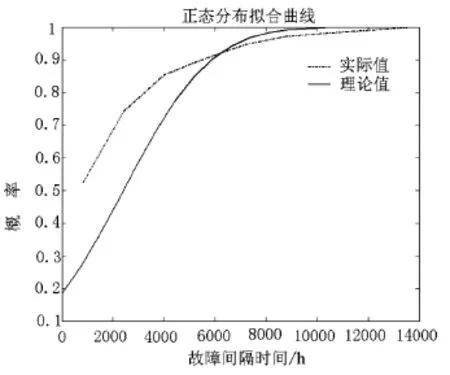
图4 正态分布拟合曲线

通过MATLAB的运行结果为h=1，即拒绝原假设，原假设成立的概率为p=2.3644e－010。因此，可以判断正态分布不能正确描述风电机组故障间隔时间的分布形式，服从正态分布的概率为p=2.3644e－10。

二、对数正态分布

对数正态分布是对正态分布的一种变形，它是指产品寿命的对数服从正态分布，对于产品来说，寿命不可能出现负值，所以对数正态分布在工程上更合理。若寿命ξ的对数 1nξ服从正态分布，则称ξ服从对视正态分布，即X=1nt～N(μ,σ2)。对数正态分布的分布函数为

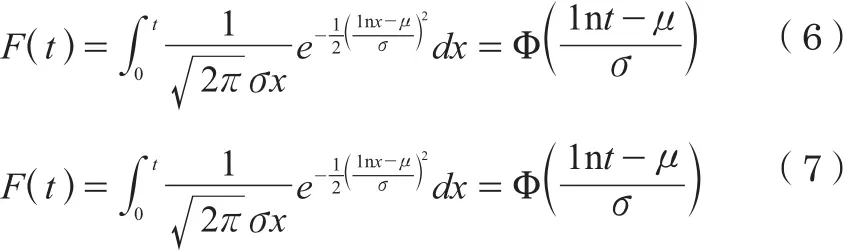
对数正态分布的两个参数分别为对数均值μ和对数方差σ2。

（一）对数正态分布参数估计

在MATLAB中，利用函数logfit对对数正态分布进行参数估计，其调用格式为

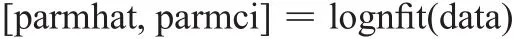
则服从对数正态分布时，运用MATLAB命令对风电机组故障间隔时间分布函数参数的估计值为：

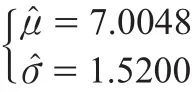
对数正态分布函数模型为

（二）对数正态分布曲线拟合

MATLAB 中，利用函数lognrnd抽取风电机组故障间隔时间服从对数正态分布时的随机数，调用函数logncdf求取对应的对数正态分布累积分布函数。利用MATLAB软件绘制出对数正态分布累积分布函数曲线，与风电机组实际的故障间隔时间累积分布曲线对比如下图5。

（三）对数正态分布假设检验

运行MATLAB对对数正态分布模型进行K－S假设检验，其检验结果为h=1，即拒绝原假设，原假设成立的概率为p=0.0222。所以对数正态分布函数不能有效描述风电机组故障间隔时间的分布形式，服从对数正态分布的概率为p=0.0222。

三、双参数威布尔分布

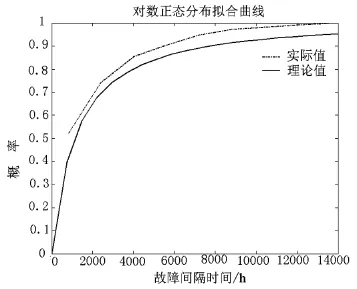
图5 对数正态分布拟合曲线

图6 双参数威布尔分布拟合曲线

威布尔分布是在可靠性工程中非常重要的一种分布形式，由于威布尔分布和其他分布的关系比较密切，且其形状参数取值范围反映了产品的失效特性，因此威布尔分布对各种类型试验数据的适应能力较强，可以模拟多种失效率的变化形式。

威布尔分布的分布函数为

威布尔分布有三个参数，m称为形状参数，η为尺度参数，γ为位置参数。当γ=0时，称其为双参数威布尔分布。

所以，双参数威布尔分布分布函数为

（一）威布尔分布参数估计

在MATLAB中，双参数威布尔分布可以调用函数wblfit来进行参数估计，该命令用极大似然法给出了其分布参数的点估计和区间估计。

调用格式为则服从双参数威布尔分布时，运用MATLAB对风电机组故障间隔时间分布函数参数的估计结果为：双参数威布尔分布模型为

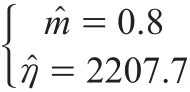
（二）威布尔分布曲线拟合

在MATLAB 中，利用函数wblrnd抽取风电机组故障间隔时间服从威布尔分布时的随机数，调用函数wblcdf求取对应的威布尔分布累积分布函数。利用MATLAB绘制出运行威布尔分布累积分布函数曲线，与风电机组实际的故障间隔时间累积分布曲线对比如下图6。

(三)威布尔分布假设检验

运行MATLAB对威布尔分布模型进行K－S假设检验，其检验结果为h=0，即接受原假设，且原假设成立的概率p=0.9735。因此，可以判断双参数的威布尔分布函数能准确描述风电机组故障间隔时间的分布形式，服从双参数威布尔分布的概率为p=0.9735。

通过上述的分析比较，最终确定了风电机组故障间隔时间的分布形式为双参数的威布尔分布，其分布函数为

结语

本文根据收集到的某风电场30台风电机组52个月的运行数据，提取出其故障间隔时间，并作出了它的相对频率直方图和累积故障频率分布图。通过与常见分布函数曲线的比较，初步确定了风电机组故障间隔时间的三种分布形式。并且运用MATLAB软件对三种分布形式进行参数估计、曲线拟合和假设检验。通过分析比较，发现双参数的威布尔分布函数能够准确的描述风电机组故障间隔时间的分布形式，最终确定了风电机组故障间隔时间的分布函数。通过这种方法能快速、准确的确定风电机组故障间隔时间的分布模型，为风电机组的设计制造、维护提供了理论依据。

（作者单位：兰州理工大学机电工程学院）