管道泄漏污染物一维迁移的LBM模拟

齐晗兵，刘 杰，李 栋，袁兆成，刘 洋

（东北石油大学 土木建筑工程学院，黑龙江 大庆 163318）

管道泄漏污染物一维迁移的LBM模拟

齐晗兵，刘 杰，李 栋，袁兆成，刘 洋

（东北石油大学 土木建筑工程学院，黑龙江 大庆 163318）

石油管道泄漏现象时有发生，对环境造成了危害，研究埋地管道石油污染物泄漏尤为关键。在此采用Boltzmann研究方法，通过多尺度技术和局部平衡态分布函数的Chapman-Enskog展开得到运算的平衡态方程，并给出了石油管道污染物泄漏迁移的一维有源扩散方程的格子Boltzmann模型，通过C++软件数值模拟进行运算。最终得出结果与理论解一致，验证了用Boltzmann方法研究污染物泄漏迁移的可行性。

污染物泄漏迁移；格子Boltzmann方法；平衡态方程；数值模拟

埋地输油管道发生泄漏事故后引发的一系列环境污染，都直接或者间接地影响当地居民的正常生活，在短时间内很难消除泄漏事故带来的影响[1,2]。研究者们从不同角度对这种污染进行了研究，为治理污染及修复已被污染的土壤提供了可靠的依据。很多学者在研究石油污染物扩散，用到了实验的方法或用FLUENT等软件进行模拟。

传统的计算流体力学方法是对宏观连续性方程的离散，而LBM是基于统计物理，并以极其简单的形式描述粒子的微观行为，但在宏观层次上正确反映流体的运动。格子Boltzmann方法发展20年来已经成为了一个十分活跃和极具发展前景的模拟手段，LBM（Lattice Boltzmann Method）计算简单，本质并行和易于处理边界的优点[3]，在许多领域的各种数值问题求解上取得很大的成功[4,5,6]，尤其对复杂边界和复杂流场，如湍流、多相流、多孔多介质流、化学反应流、燃烧、非牛顿流等许多领域得到应用，为计算流体力学的数值模拟开辟了一条革命性的道路[7]。

本文采用 LBM研究埋地管道石油污染物泄漏迁移扩散的一维模型。LBM算法具有高度的并行性，能得出清晰的物理图像，可将一维模型继续扩展为二维和三维来对其进行研究，为石油污染物泄漏迁移研究提供依据。有源扩散方程是在研究污染物泄漏常用的扩散方程，一维情况通常如下：

式中: u—粒子迁移速度， 表示扩散系数；

q(x) —扩散源项。

针对埋地石油管道泄漏污染物迁移提出污染物扩散方程，模拟污染源扩散项为：。针对一维污染物扩散方程，结合提出的石油污染物扩散源项，得出如下方程：

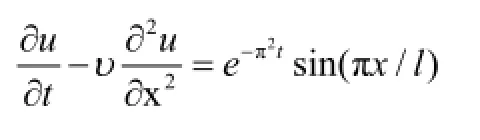
1 格子Boltzmann方法和运用多尺度技术的守恒方程

本文研究污染物扩散一维情况，采用格子Boltzmann方法，用D1Q3模型，将一维空间均匀等分，其中速度配置e[k]=[-1,0,1]，分别表示例子向左、不动、向右三种情况，并且满足如下情况：

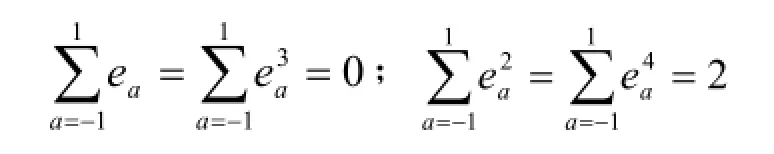
由物理统计知，分布函数的弛豫形式 Boltzann方程演化如下：

式中f（0）（x，ea，t）为平衡态分布函数，后文简写为fa（x，t）或者fa，方程式中的弛豫时间τ≥0.5可满足稳定性要求。

将弛豫形式Boltzann方程（1）左边在（x，t）处按照Taylor级数展开二级项[8]：

采用多尺度技术：

将（3）带入（2），求出一阶和二阶小参数（ε）下的函数方程：

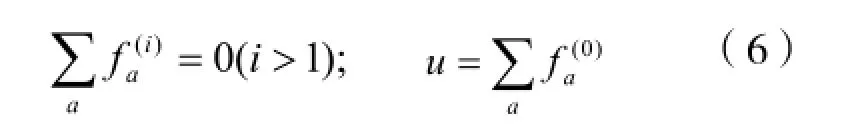
对（4）两边a求和，利用(6)计算出：

结合（6）推导出守恒方程：

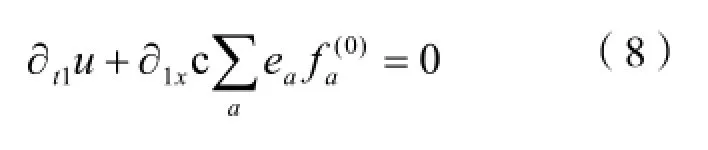
将（5）两边的对a求和推到可得出：

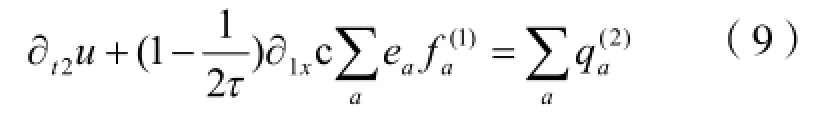
2 Chapman-Enskog（CE）展开得出局部平衡态分布函数

通过CE展开平衡分布函数可得如下形式[9]：

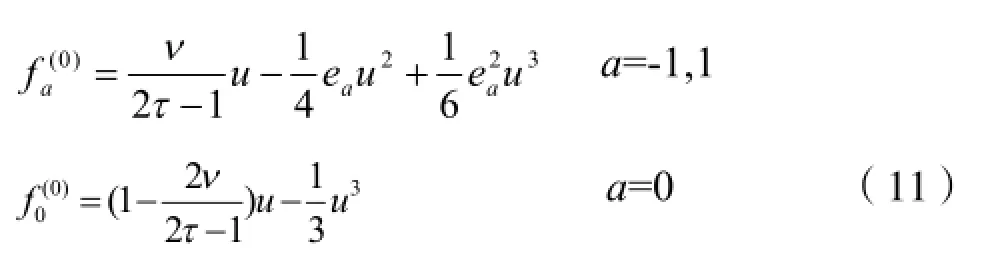
3 模型验证以及结论

计算模型以及边界条件如下[10]：

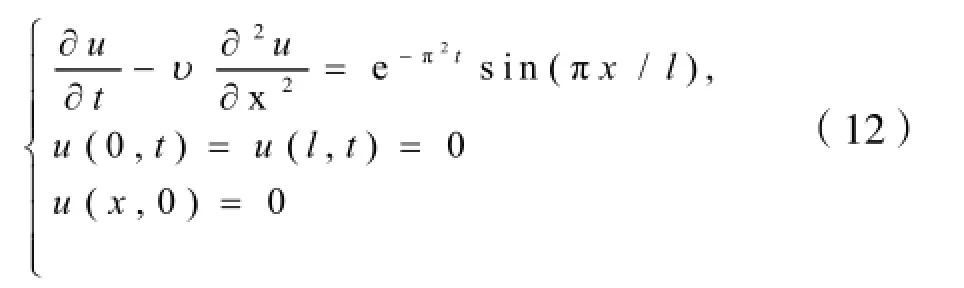
通过LBM算法和数值解的对比，采用实际时长是0.24 s时的计算数据，将一维的网格划分10段11个点进行boltzmann方法数值模拟，坐标量纲为1,并且引用高精度差分方法[11]（时间步长0.01，空间步长0.1）进行计算得出结果，三者对比发现LBM方法的结果与理论数值和高精度方法得出的数据一致性很好，其中绝对误差ε=|解析解-LBM模拟解|，绝对误差。得出如图1、表1数据结论。

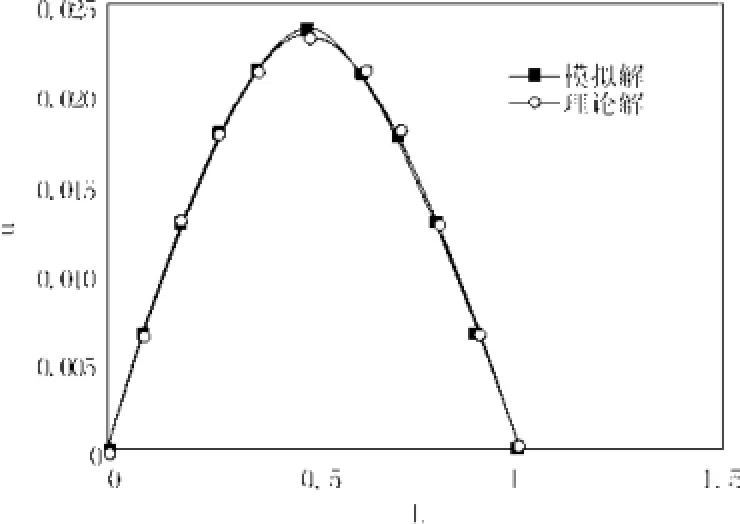
图1 理论值与模拟值对比（t =0.24）Fig.1 The contrast of theoretical value and simulation value （t =0.24）

本文还利用LBM计算了 t =0.15和 t =0.3 时刻的污染物泄漏迁移速率，并且与理论数值解进行对比，得出如下图2-3。

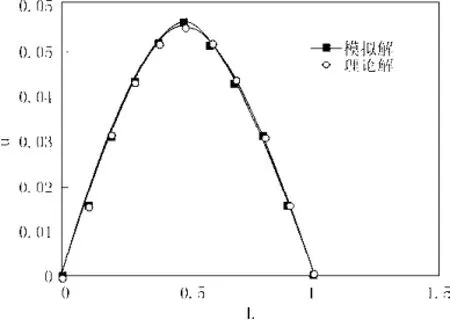
图2 理论值与模拟值对比（t =0.15）Fig.2 The contrast of theoretical value and simulation value （t =0.15）

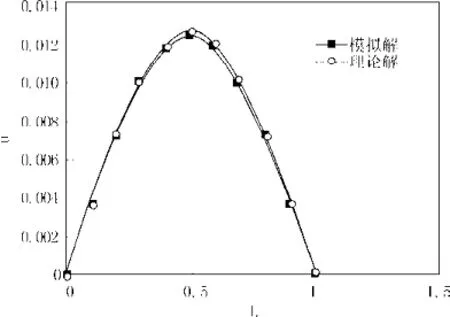
图3 理论值与模拟值对比（t =0.3）Fig.3 The contrast of theoretical value and simulation value （t =0.3）

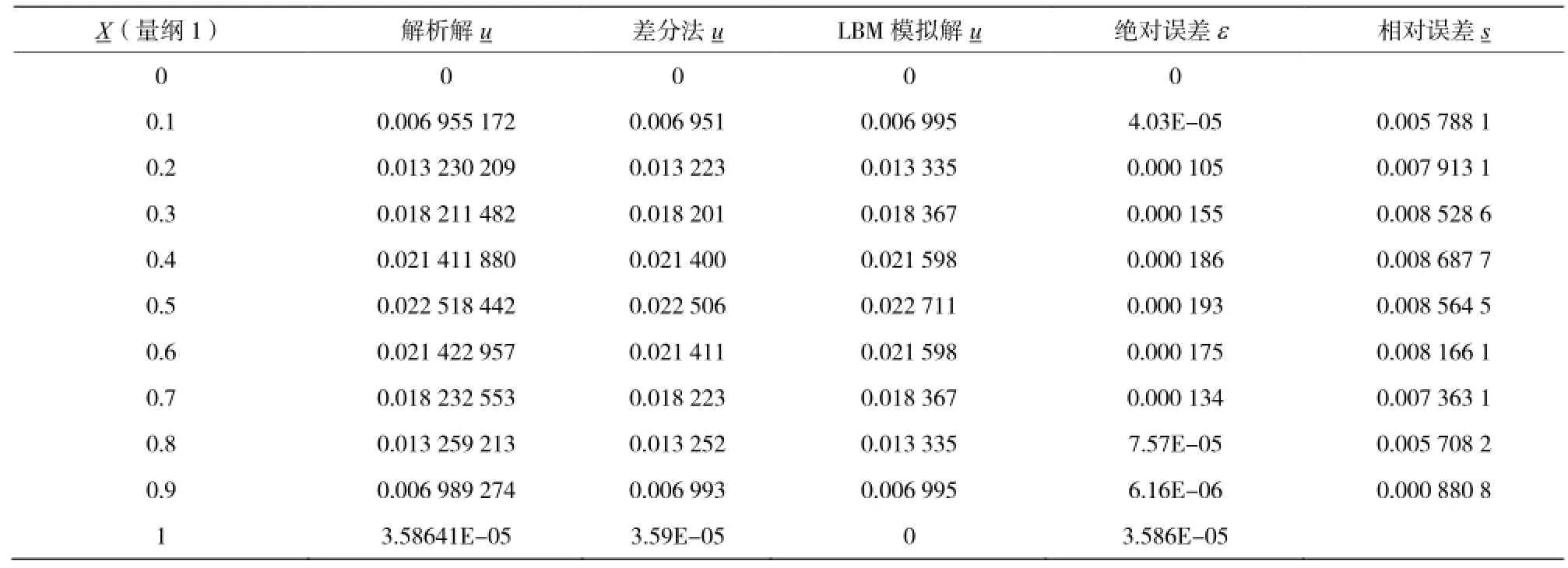
表1 解析解与LBM 数值模拟对比Table 1 The comparison of analytical solution and LBM numerical simulation

通过以上表和图知，Boltzmann方法较好的计算出了石油管道污染物一维迁移的速率值，与理论解比较误差很小，一致性良好。此方法的可行性为研究石油管道泄漏污染物的迁移提供理论依据。

［1］Jones. Inspection. A Smart Investment. The Third British Gas International Conference on pipeline Inspection[C]. Assessment and Repair,1996-06: 25-27.

［2］王莉莉. 管道泄漏检测技术的研究[D]. 大连：大连理工大学，2010: 1-2．

［3］何雅玲，王勇，李庆. 格子Boltzmann方法理论及应用[M]. 北京：科学出版社（当代杰出青年科学文库），2008.

［4］Doolen G D. Lattice gas and lattice Boltzmann for partial diffrential equation[J]. Physica D, 1991,47:1-200.

［5］Lebowitz, Orsazag S A, Qian Y H. Program of the lattice gas.94 meeting at Princeton[J]. J Stat Phys, 1995,68:1-536.

［6］Chen H, Chen S,MattheausH. Recovery of Navier-Stokes equation using a lattice-gas Boltzmann method[J]. PhysRev E, 1992,45:5 339-5 341.

［7］段雅丽. 格子Boltzmann方法及其在流体动力学上的一些应用[D].合肥：中国科学技术大学，2007:2-6.

［8］陈若航，刘慕仁. 用多尺度技术建一维对流扩散方程的格点模型[J].广西师范大学学报(自然科学版)，1997, 15（2）.

［9］梁宝社，何枉泉，刘书声. 利用chapman一Enskog展开求解粒子平衡分布函数[J].河北建筑科技学院学报，1998,15(4).

［10］杨志峰等. 含源扩散方程的一种高精度差分方法[J].北京师范大学学报,1992,28(1).

［11］田振夫，魏淑清. 含源扩散方程的一类高阶紧致差分格式[J].宁夏大学学报(自然科学版)，1997,18(3).

One-dimensional LBM Simulation of Buried Pipeline Leak Pollutant Migration

QI Han-bing，LIU Jie，LI Dong，YUAN Zhao-cheng，LIU Yang
（School of Architecture and Civil Engineering，Northeast Petroleum University，Helongjiang Daqing 163318, China）

Oil pipeline leak phenomenon has harm to the environment, so it is important to study buried pipeline leak oil pollutants. In this paper, based on Boltzmann method, the one-dimensional lattice Boltzmann model diffusion equation of oil pipeline leakage pollutant migration was given, the equilibrium equation was computed through multi-scale technique and partial equilibrium distribution function of Chapman Enskog expansion, and numerical simulation calculation was carried out by C + + software. Finally it’s concluded that the results are consistent with the theoretical solution, which can verify the feasibility of Boltzmann method to study the leakage pollutant migration.

Leakage pollutant migration; Lattice Boltzmann method; Equilibrium equation; Simulation

TE 832

A

1671-0460（2014）12-2721-03

国家自然科学基金 (No. 51274071)

2014-05-29

齐晗兵（1975-），男，黑龙江齐齐哈尔人，教授，博士，2009年毕业于东北石油大学油气储运工程专业，研究方向：长输管道传热计算、油气田地面管网系统优化、油气储运系统节能。E-mail：qihanbing@sina.com。