L型阵列双基地MIMO雷达的传播算子多维角度估计

孙中伟， 张小飞， 吴海浪， 李建峰

南京航空航天大学电子工程系，南京210016

多输入多输出(multiple-input multiple-output,MIMO)雷达使用多根天线同时传送和接收波形信号[1]，具有超过传统相控阵的潜在优势.MIMO雷达比只有一种发射波形的雷达系统有更多的自由度，而这些额外的自由度能有效克服衰落的影响，提高空间分辨率，增强参数可辨识性，并改进目标检测性能[2-5].文献[6-9]介绍了MIMO雷达的离开角(direction of departure,DOD)和到达角(direction of arrival,DOA)估计算法的研究现状.其中，文献[6]提出了多信号分类(multiple signal classif ication,MUSIC)算法，通过子空间进行角度估计，具有良好的估计性能.二维(two-dimensional)MUSIC算法可用于DOD和DOA的估计，但计算复杂度很高.文献[8]借助旋转不变技术估计信号参数(estimating signal parameter via rotational invariance techniques,ESPRIT)算法，根据旋转不变性实现MIMO雷达中的角度估计，且实现参数的自动配对.文献[9]提出了传播算子(propagator method,PM)算法，不必对协方差矩阵进行特征值分解，故运算量小.文献[10]提出了一种基于传播算子的双基地MIMO雷达快速多目标定位算法，使用均匀线阵只实现了发射和接收方向上的一维角度估计，而实际应用中需要二维的DOA和二维的DOD.

本文提出一种在L型阵列下的通过PM能够实现四维角度估计且角度自动配对的算法，既不需要额外的配对运算就实现了参数的自动配对，又不需要对协方差进行特征值分解，故运算量小.与ESPRIT算法相比，本文算法的复杂度较低，在高信噪比情况下的性能接近ESPRIT算法.

1 数据模型

考虑发射和接收阵列都是L型阵列，包含2M-1根发射天线和2N-1根接收天线的双基地MIMO雷达系统，发射阵列在x轴上有M根天线，在y轴上也有M根天线；接收天线在x轴上有N根天线，在y轴上也有N根天线，并且天线间隔均为d=λ/2.在实际应用场合中，信源数往往是一个未知数，需要先估计信源数的数目或者假设已知，此处假设已知K个不相关信源.

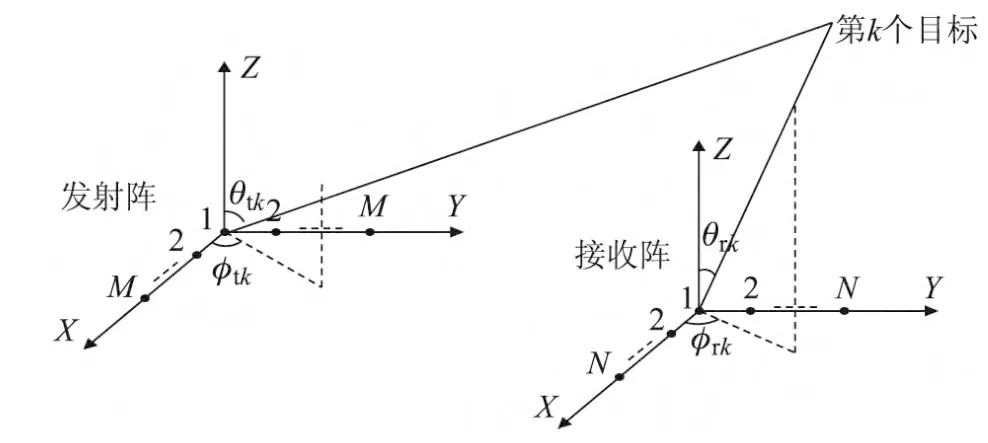
图1 MIMO双基地雷达L型阵列图Figure 1 Bistatic MIMO radar with L-shaped array

发射端发射正交窄带波形，取快拍数为L，则匹配滤波后的接收接收信号为

式中，A为方向矩阵，具体形式为

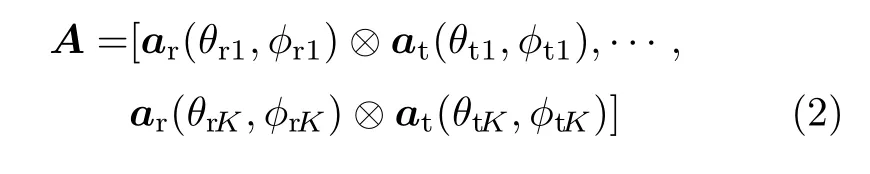
式中，ar(θrk,φrk)⊗at(θtk,φtk)为第k个目标接收矢量与发射矢量的Kronecker积，其中

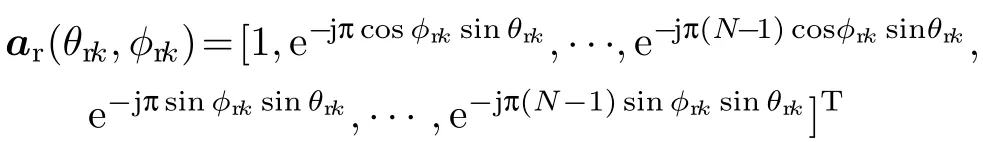
式中，θrK和φrK为接收阵列接收到的第k个目标的仰角和方位角；θtK和φtK为第k个目标对于发射阵列的仰角和方位角；S为信号源矩阵，N为噪声矩阵，是均值为零、方差为σ2I(2M-1)(2N-1)的加性高斯白噪声矢量；方向矩阵A也可以表示为

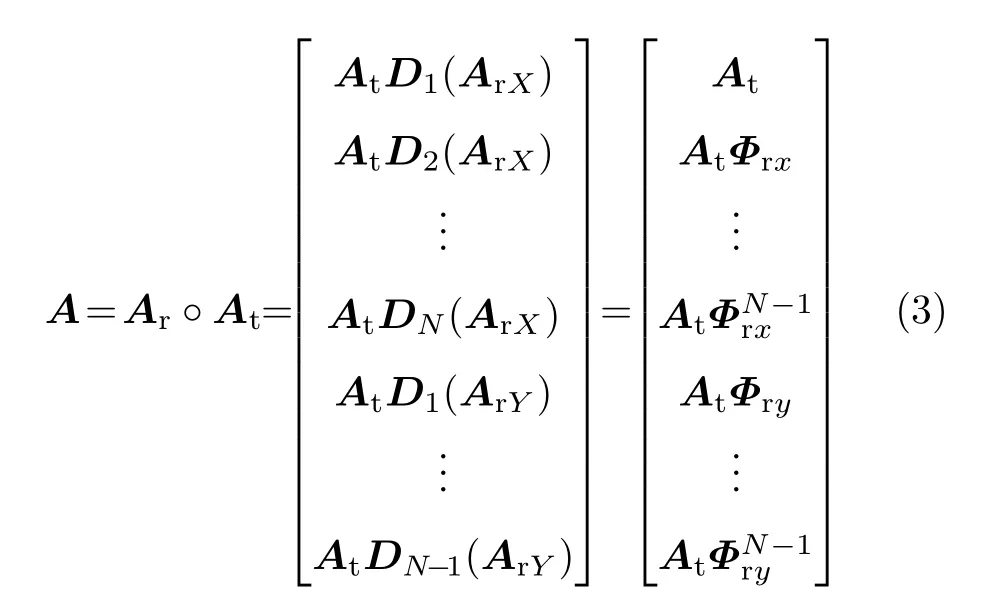
式中，At=[at(θt1,φt1),at(θt2,φt2),···,at(θtK,φtK)]和Ar= [ar(θr1,φr1),ar(θr2,φr2),···,ar(θrK,φrK)]分别为发射方向矩阵和接收方向矩阵，也可表示为为发射阵列x轴方向上的方向矩阵，AtY为发射阵列y轴方向上的方向矩阵，ArX为接收阵列x轴方向上的方向矩阵，ArY为接收阵列y轴方向上的方向矩阵；Dm(·)是取矩阵的第m行组成一个对角矩阵,

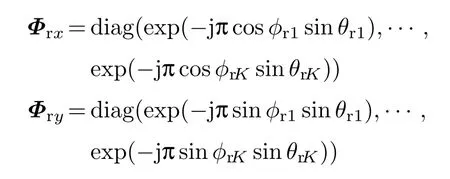
式中，diag(·)表示对角化矩阵.

2 双基地M IM O雷达中的多维角度估计算法

由传播算子估计DOD和DOA，先估计传播算子；再将A分块，其中A1和A2分别为K×K和((2M-1)(2N-1)-K)×K维的矩阵

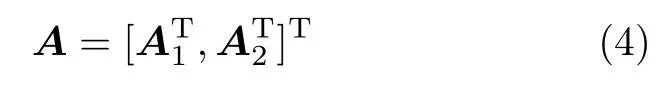
假设A1是非奇异矩阵，则A2为A1的线性变换，可得

式中，Pc即为传播算子，令P=[IK,PTc]T，其中IK为K阶单位矩阵.根据式(4)和(5)可得

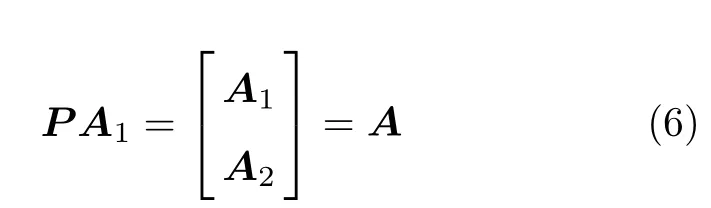
对P进行分块可得

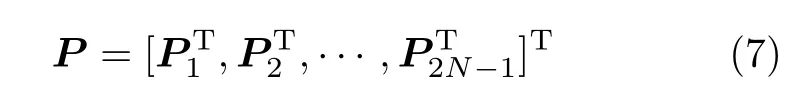
式中，Pn∈C(2M-1)×K，n=1,···,2N-1；根据式(6)的对应关系可得

2.1 二维DOA估计

根据式(8)的对应关系可得

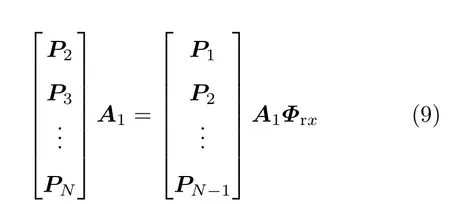
定义Ψrx=Pb，Ψrx和Φrx有相同的特征值，对Ψrx进行特征值分解，得到特征值矩阵；定义λk为第k个对角线元素，与Φrx对角线的值一一对应，同时可以求得特征向量A1的估计值.在无噪声的情况下，有

式中，Π为列模糊矩阵且Π-1=Π，则估计得到的特征值矩阵=ΠΦrxΠ，方向矩阵A的估计矩阵为

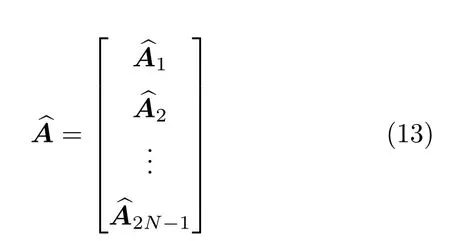
令rk为的第k个对角线元素，且λk和rk对应于同一个目标.由λk和rk可得

式中，angle(·)表示取相角，由此可以估计出第k个目标DOA的仰角和方位角

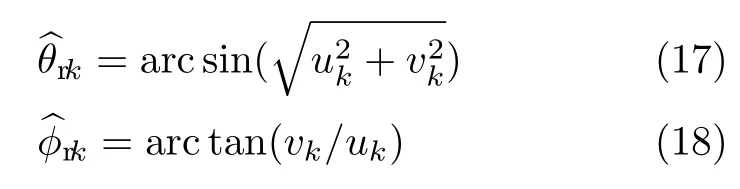
此时已经估计出DOA的仰角和方位角，且已实现了参数的自动配对.

2.2 二维DOD估计

下面对接收阵列的方向矩阵进行重构得到发射阵列的方向矩阵，估计出发射阵列的方位角和仰角.存在一个行交换矩阵E使得式(19)成立

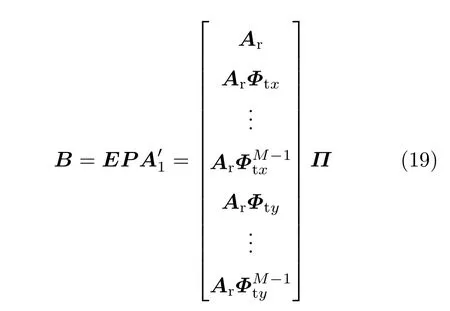
式中，Φtx=diag(exp(-jπcosφt1sinθt1),···,exp(-jπ·cosφtKsinθtK))，Φty=diag(exp(-jπsinφt1sinθt1),···,exp(-jπsinφtKsinθtK)).

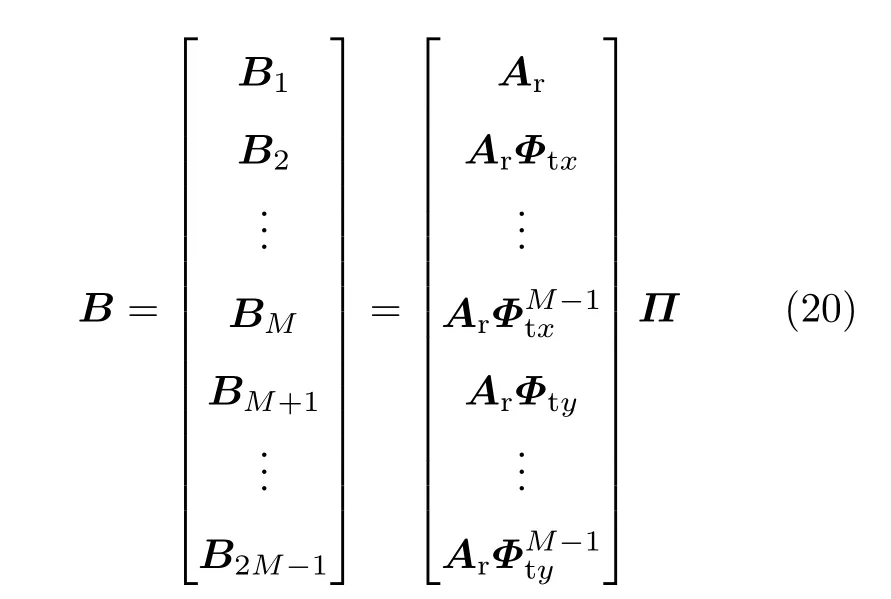
根据式(20)可得

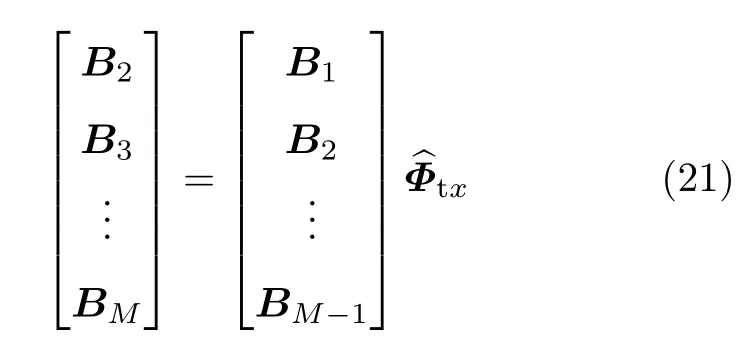
令δk为的第k个对角线元素，δk、λk、rk对应于同一个目标；由式(20)还可以得到关系式

定义σk为的第k个对角线元素，σk、δk、λk、rk对应于同一个目标，从而实现了四维角度的自动配对.由已经求出的δk和σk得到

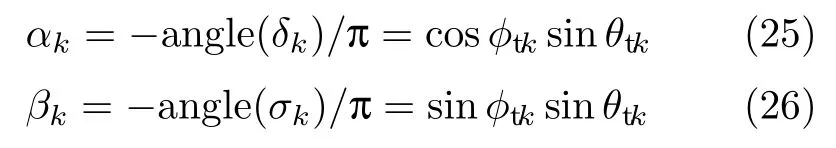
估计出发射阵列的仰角和方位角为

2.3 传播算子实现四维角度估计算法

至此，已经给出了双基地MIMO雷达中基于PM的四维角度估计算法.将算法步骤总结如下：

步骤3 根据式(19)重构得到B，构造Ba和Bb，由式(22)估计出，相似地通过构造Bc和Bd，由式(24)估计得到，通过式(27)和(28)估计出DOD.

2.4 复杂度分析

与ESPRIT算法相比，本文算法的复杂度低,主要集中在协方差矩阵运算、传播算子估计、特征值分解和求广义逆运算，参数配对不需要额外的运算，其复杂度为：O((2N-1)2(2M-1)2L+(2N-1)2(2M-1)2+K2(2M-1)(2N-1)+3K2(M-1)(2N-1)+3K2)，ESPRIT算法的复杂度为O((2N-1)2(2M-1)2L+(2N-1)3(2M-1)3+3K2(M-1)(2N-1)+2K2).

3 误差分析

此节对仰角和方位角的估计误差进行分析.假定

P=P+∂P，∂P为传播算子误差矩阵.由式(8)可知

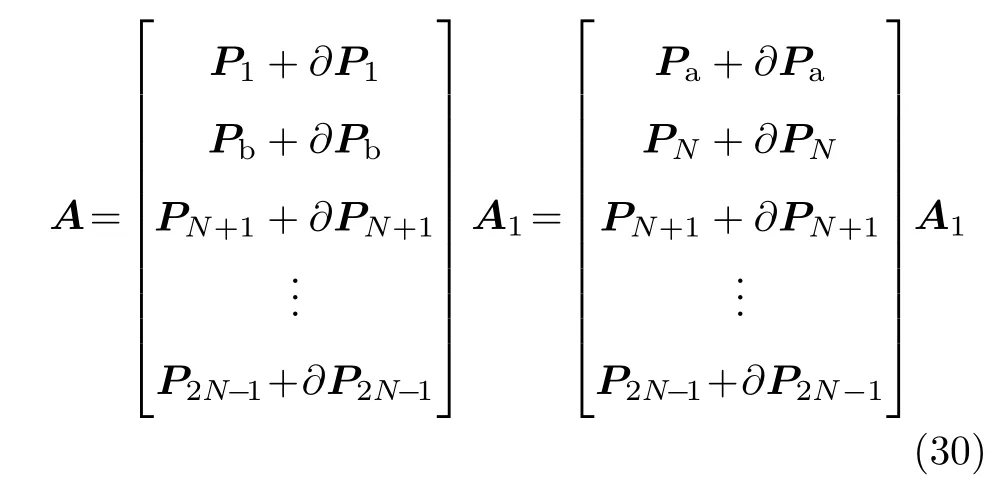
式中，∂P1、∂PN、∂PN+1、∂P2N-1分别表示∂P的第1组、第N组、第N+1组、第2N-1组、2M-1行.由[Pa+∂Pa]+的一阶近似得

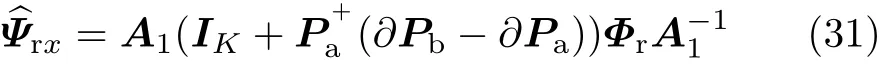
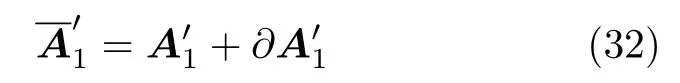
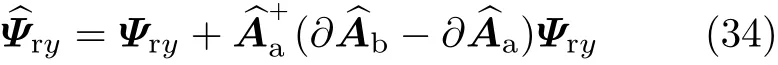
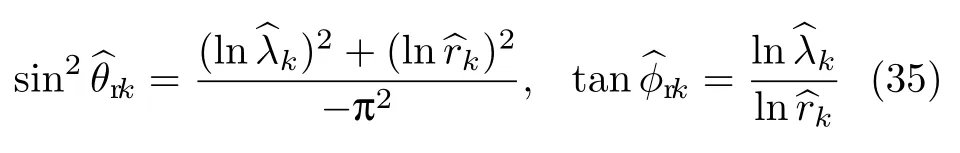
使用一阶Taylor级数展开，经计算可求得DOA的仰角和方位角估计均方误差.仰角的估计均方误差为

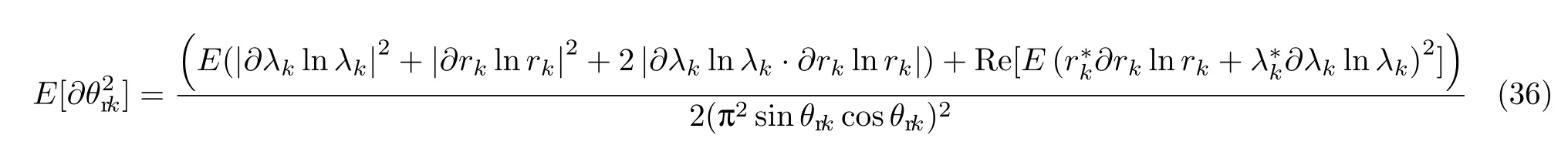
方位角的估计均方误差为

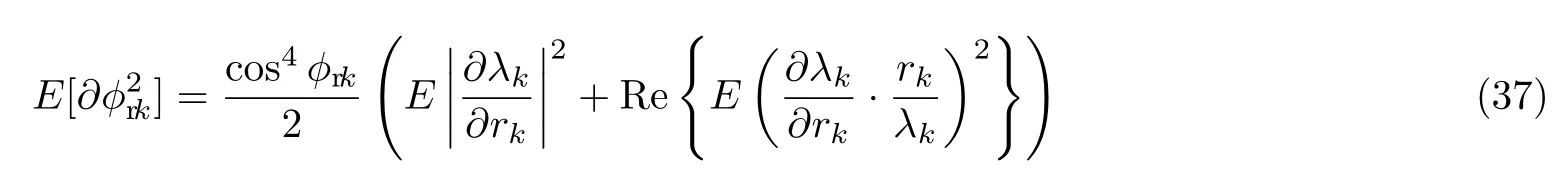
式中，∂θrk为θrk的误差估计,∂φrk为φrk的误差估计.同理可以估计出DOD的仰角和方位角的估计均方误差，DOD仰角的估计均方误差为

DOD方位角的估计均方误差为

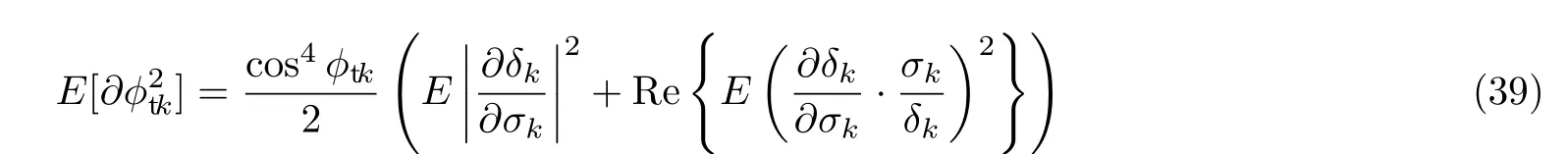
式中，∂θtk为θtk的误差估计,∂φtk为φtk的误差估计.

定义A=[a1,a2,···,aK]，其中ak是矩阵A的第k列.根据文献[13]推导了MIMO雷达的角度估计的克拉美罗界(Cramér-Rao lower bound,CRB)

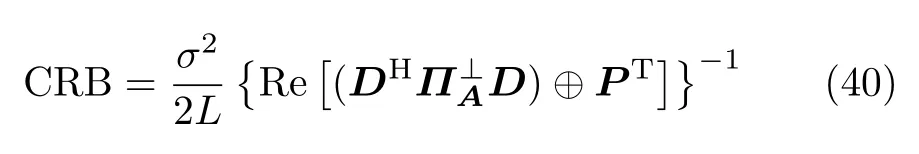
式中，⊕为Hadamard积，Π⊥A=I-A(AHA)-1AH,P=s(tl)sH(tl).D=[d1,d2,···,dK,f1,f2,···,fK,e1,e2,···,eK,g1,g2,···,gK],dk= ∂ak/∂θtk,fk=∂ak/∂φtk,ek=∂ak/∂θrk,gk=∂ak/∂φrk.

4 仿真结果

仿真1 图2给出了本文算法在信噪比(signal to noise ratio,SNR)为5 dB时的仿真结果.3个目标DOA和DOD对选择为(10°,20°,5°,25°)、(20°,30°,5°,35°)、(30°,40°,5°,45°)，采用50次蒙特卡罗仿真，其中M=8、N=6、K=3、L=100.图3给出了本文算法在3个目标DOA和DOD对(15°,20°,7°,22°)、(25°,10°,7°,12°)、(35°,30°,7°,32°)下的角度估计性能.由图2和3可以看出，此算法可以有效估计MIMO系统的离开角和到达角；即使在信噪比低(SNR=5 d B)的情况下，本文算法角度估计的性能仍然良好.

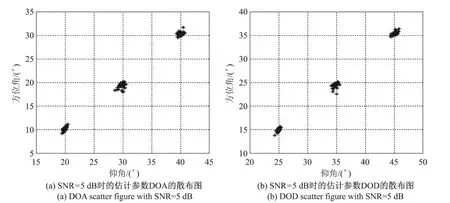
图2 信噪比为5 d B时的估计角度散布图Figure 2 Estimated angles of the scatter plot when SNR=5 d B

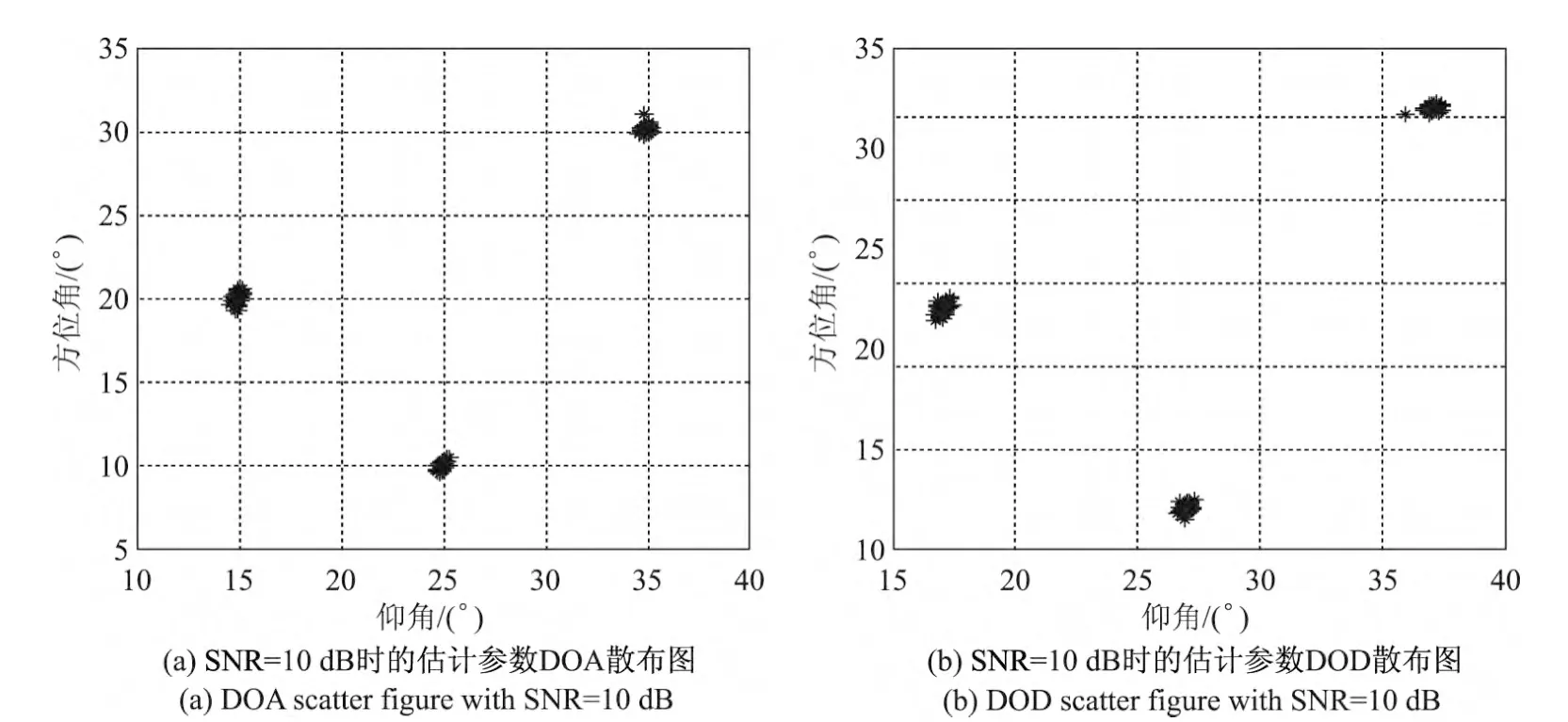
图3 信噪比为10 d B时的估计角度散布图Figur e 3 Estimated angles of the scatter plot when SNR=10 d B

在仿真2和3中，考虑到3个目标，它们的DOA和DOD对为(10°,20°,5°,25°)、(20°,30°,5°,35°)、(30°,40°,5°,45°).本文进行5 000次蒙特卡罗仿真来估计本文算法的角度估计性能，定义

式中，^αmk和^βmk为第m次蒙特卡罗仿真时第k个目标相对发射阵/接收阵仰角和方位角的估计值，αk和βk为第k个目标的仰角和方位角的真实值.

仿真2 图4比较了本文算法、ESPRIT算法和克拉美罗界(Cramér-Rao lower bound,CRB)的性能，在本次仿真中取M=8、N=6、K=3、L=100；由图4可以看出，在低信噪比情况下，本文算法的性能低于ESPRIT的算法性能；当信噪比较大时，本文算法的性能与ESPRIT算法性能相接近.

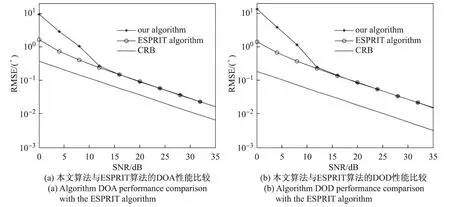
图4 本文算法与ESPRIT算法的角度估计性能比较Figure 4 Algorithm angles performance comparison with the ESPRIT algorithm

仿真3 图5给出了不同快拍数L情况下的角度估计性能，其中M=8、N=6、K=3；由图5可以看出，随着快拍数L的增加，角度估计的性能变好，即使在快拍数很小(L=10)的情况下，此算法仍能保持良好的估计性能.

仿真4 图6显示了传播算子误差矩阵对角度估计性能的影响，仿真参数同仿真2.从图6中可以看出，随着传播算子误差矩阵的功率的增加，本文算法的角度估计性能逐渐下降.

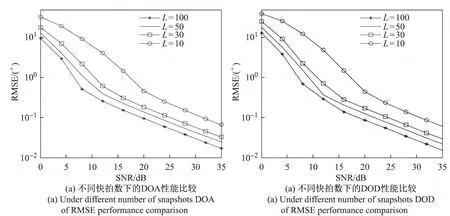
图5 不同快拍数下的角度性能比较Figure 5 Under different number of snapshots angles of RMSE performance comparison

5 结语

本文将PM算法引入双基地MIMO雷达，用于L型阵列下的多维DOD和DOA的估计，并实现了多维角度的自动配对.由协方差矩阵估计出传播算子，利用传播算子的旋转不变性计算出方向矩阵，进而求出二维DOD和二维DOA.不需要对协方差矩阵进行特征值分解，就可以估计出四维角度，而且不需要额外的配对运算，就能实现角度的自动配对.与普通的PM算法相比，本文算法能估计出多维的角度信息，且算法精度有所提高.算法性能在高信噪比情况下与ESPRIT算法性能相近，但运算量低于ESPRIT算法，且在目标相近的情况下仍能保持良好的性能.

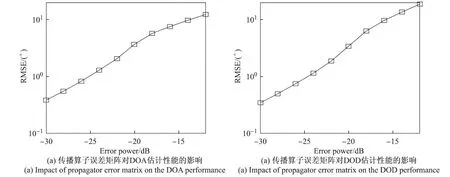
图6 传播算子误差矩阵对角度估计性能的影响Figure 6 Impact of propagator error matrix on the angles performance

[1]FISHLER E,HAIMOVICH A,BLUM R S,CIMINI L J,CHIZHIK D,VALENZUELA R A.MIMO radar:an idea whose time has come[C]//Proceedings of IEEE Radar Conference,2004:71-78.

[2]LI Xiangru,ZHAOZhang,WUXingmao,WANG Xiaomo,LU Jun,WANG Wensheng.A study of frequency diversity MIMO radar beam forming[C]//2010 IEEE 10th International Conference on Signal Processing(ICSP),2010:352-356.

[3]SHARMAR.Analysis of MIMO radar ambiguity functions and implications on clear region[C]//2010 IEEE International Radar Conference,2010:544-548.

[4]ROBERTS W,LI J,STOICA P,YARDIBI T,SADJADI F A.MIMO radar angle-range-Doppler imaging[C]//2009 IEEE International Radar Conference,2009,5:1-6.

[5]WU X H,KISHK A A,GLISSON A W.MIMOOFDM radar for direction estimation[J].IET Radar,Sonar&Navigation,2010,4(1):28-36.

[6]ZHANG Xiaofei,XU Linyun,XU Lei,XU Dazhuan.Direction of departure(DOD)and direction of arrival(DOA)estimation in MIMO radar with reduceddimension MUSIC[J].IEEE Communications Letters,2010,14(12):1161-1163.

[7]ZHANG Xiaofei,XU Dazhuan.Angle estimation in MIMO radar using reduced-dimension capon[J].IET Electronics Letters,2010,46(12):860-861.

[8]CHENJinli,GUHong,SUWeimin.Angle estimation using ESPRIT without pairing in MIMO radar[J].Electronics Letters,2008,44(20):1422-1423.

[9]MARCOSS,MARSAL A,BENIDIR M.The propagator method for source bearing estimation[J].Signal Processing,1995,42(2):121-138.

[10]陈金力，顾红，苏卫民.一种双基地MIMO雷达快速多目标定位方法[J].电子与信息学报，2009,31(7):1664-1668.CHENJinli,GUHong,SUWeimin.A method for fast multi-target localization in bistatic MIMO radar system[J].Journal of Electronics&Information Technology,2009,31(7):1664-1668.(in Chinese)

[11]ZHANG Xiaofei,GAO Xin,XU Dazhuan.Multiinvariance ESPRIT-based blind DOA estimation for MC-CDMA with an antenna array[J].IEEE Transactions on Vehicular Technology,2009,58(8):4686-4690.

[12]STOICA P,NEHORAI A.Performance study of conditional and unconditional direction-of-arrival estimation[J].IEEE Transactions Signal Process,1990,38(10):1783-1795.