基于类Matern点过程模型的异构蜂窝网建模
2014-02-21任承蒙张剑峰徐友云
任承蒙, 张剑峰, 王 聪, 谢 威, 徐友云
解放军理工大学 通信工程学院,南京210007
异构是4G蜂窝通信的一个关键特性,是提高终端用户吞吐量[1],拓宽室内和小区边缘覆盖的必要途径.异构蜂窝网除了常规的蜂窝网部署,还包含多种不同的低功率基站[2-3],比如微微蜂窝基站、毫微微蜂窝基站和中继基站.根据基站发射功率的高低,异构蜂窝网可以分为多层,又被称多层蜂窝网.由于部署的目的和规划不同,不同层基站的空间密度各不相同,所服务用户的目标信干噪比也不同.通常宏蜂窝(macrocell)为第1层,用于基本的覆盖,其基站拥有最大的发射功率和最小的空间密度.微微蜂窝(picocell)为第2层,其基站发射功率比宏蜂窝的小,空间密度比宏蜂窝的大.微微蜂窝主要部署在通信的热点,如商场、图书馆等,用于缓解网络负载过重导致的服务质量下降和中断概率增大.毫微微蜂窝(femtocell)为第3层,其基站发射功率最小,空间密度最大.毫微微蜂窝主要部署在家庭和办公室,用于服务特定的用户,满足其服务质量(quality of service,QoS)及对数据业务的需求.
异构蜂窝网中存在各种不同的基站,且基站的部署,尤其是微微蜂窝基站和毫微微蜂窝基站的部署没有特定的规则,这给性能分析带来了困难.近年来,关于异构蜂窝网基站的建模方法已有大量的研究.文献[4]提出的Wyner模型假设信道增益在整个网络中是个恒定的常数.这种模型不能区分小区内部用户和边缘用户,又因为信干噪比(signal and interference plus noise ratio,SINR)是固定的,所以不存在中断概率的概念.Wyner模型在没有强干扰且参数做了很多平均假设的系统中是有效的,但在有可能带有强干扰的实际系统中是不合理的,如基于OFDM的4G网络.文献[5]提出的另一个常用模型假设只取小部分干扰源的干扰和(甚至是1个)作为信道干扰,不能正确反映信道的实际情况.最常用的模型是二维六边形模型,这种模型通常应用于系统级仿真,在理论分析中也有所采用,但在异构蜂窝网的环境中其可扩展性和精确性并不好[6].文献[7]提出将基站位置抽象为一个随机点过程,由于macrocell中基站部署是规划好的,这种模型不一定适用.文献[8]通过仿真指出:即使在macrocell中,随机点分布得出的基站分布图和实际部署差距不大,于是提出了泊松点过程(Poisson point process,PPP)模型.PPP模型能够很好地反映出异构蜂窝网这种特殊网络环境下的基站分布,从而准确分析网络性能.实际上,这种PPP模型在Macrocell中只是大致接近实际部署,不可避免会出现小部分基站在建模时出现聚合的现象,而文献[8]并没有考虑这一点.在实际的基站部署中,运营商和用户都不希望出现这种导致资源浪费和严重干扰的基站聚合现象.本文引入一种既能体现异构蜂窝网基站随机分布特性,又能符合实际部署,使得基站之间保持一定距离的点过程模型,并且利用这种模型分析异构蜂窝网性能.
1 类M atern点分布
如图1所示,密度为λ的泊松点过程φ有以下2条性质:
性质1 在有限集合A⊂R2(A为区域内某个范围面积)中,点的数量服从泊松分布,均值为λ|A|,即
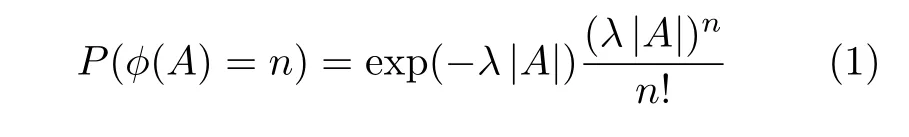
式中,φ(A)为A中点的数目.
性质2 对于区域内不相交的两个有限集合A⊂R2和B⊂R2,A和B中点的数目是不相关的.
可以看出,泊松点过程的特性仅由它的密度λ决定.
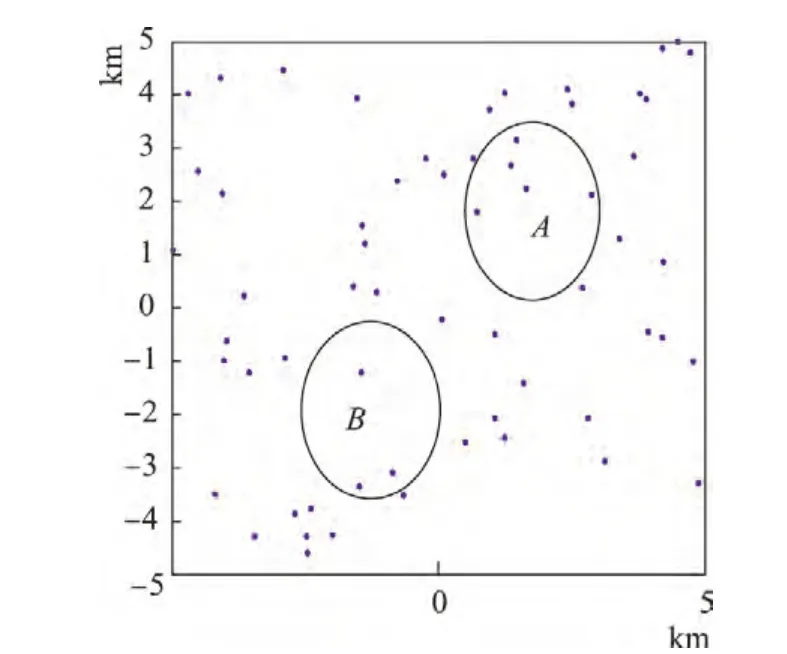
图1 密度为λ的PPPFigure 1 PPP with the density ofλ
类Marten点分布(Matern-like point process,MLPP)对PPP模型进行了改进,其主要思路是:如果两点之间的距离小于一个给定值,则按一定规则去掉其中的一个点,最终得到的就是MLPP.实际上,MLPP是PPP的一个稀释结果,其算法步骤如下:
步骤1 首先生成一个密度为λP的泊松点过程ΦP.
步骤2 对于ΦP中任意点x∈ΦP,增加一个标记mx∈U[0,1],各点之间的标记是相互独立的.
步骤3 对于圆B(x,R)中的各点,如果点x∈ΦP的标记最小,则该点保留,其余点去掉.
其中,U[0,1]表示0~1之间的均匀分布,R为给定的最小距离,即稀释半径.选点的方法可以归纳为

式中,Ψ表示在圆B(x,R)中选择保留的点,依此方法可以得出所有被选择保留的点,则所有剩余的点构成的分布模型就是MLPP模型.
图2为MLPP算法示例,图中共有10个节点,每个节点有一个随机的标记值,稀释半径R为给定值.图(a)中虚线圆圈表示该节点稀释半径内存在标记值比该节点标记值小的节点,此时可去除该节点.如标记值为0.3的节点,其稀释半径内存在标记值为0.2的节点,因此标记值为0.3的节点应去除.图(b)中圆形节点表示稀释剩余的节点,三角形节点表示去除的节点,最终剩下6个节点.
图3给出了PPP模型,可以清晰地看到有的点之间距离太小.在实际的基站部署中,如果宏蜂窝基站位置过于靠近,那么将带来严重的干扰和资源浪费,由此可知PPP模型在用于蜂窝网基站部署建模中不是一个理想的模型.图4给出了MLPP模型,可以看到该模型有效解决了PPP模型带来的问题,由于每个点之间的距离都不会太小,这将很好地控制基站间的干扰.在MLPP模型中,虽然基站的数量减小了,但系统的性能不但没有降低,反而有所增加,这将在后面的仿真分析中详细说明.
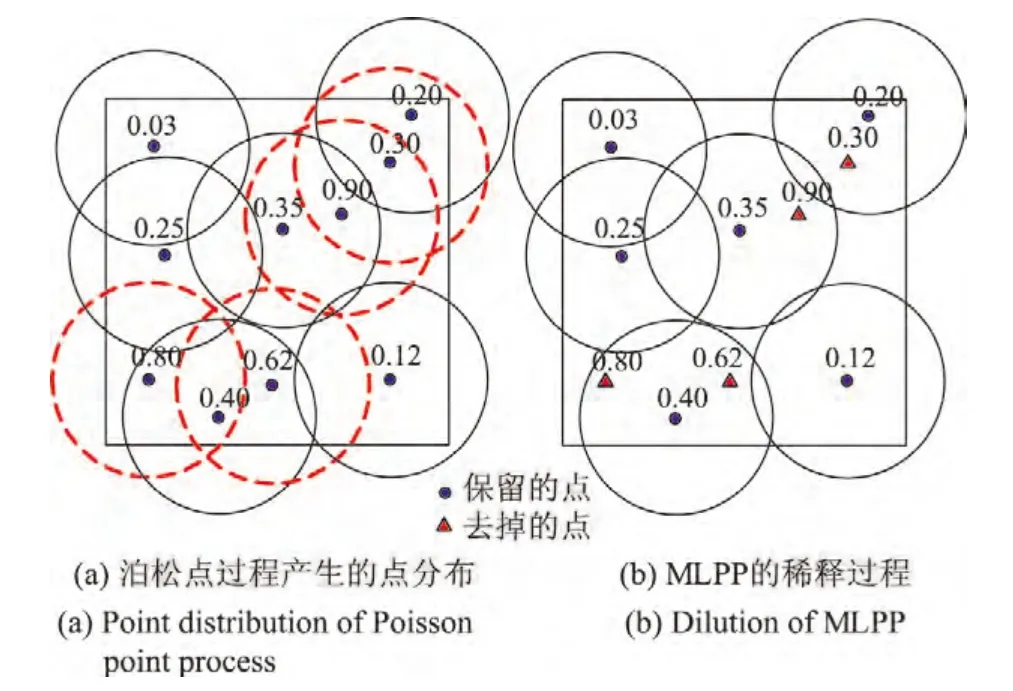
图2 MLPP算法示例Figure 2 Example of MLPP algorithm

图3 PPP模型Figure 3 PPP model

图4 MLPP模型Figure 4 MLPP model
2 两层异构蜂窝网系统模型及分析
2.1 两层异构蜂窝网系统模型
本文研究宏蜂窝和毫微微蜂窝共同组网的异构蜂窝网系统,可建模为两层异构蜂窝网系统.在实际的基站部署中,毫微微基站的位置随机性比较强.因此,对于毫微微蜂窝,仍采用PPP模型;而对于宏蜂窝,将使用MLPP模型,并将基站间最小距离设为R.假设宏蜂窝是第1层,毫微微蜂窝是第2层.每一层的基站具有不同的发射功率p,不同的分布密度λ和不同的目标信干噪比β.一个两层的异构蜂窝网系统可以建模为集合本文采用以下3条假设:假设1 噪声相对于干扰来说是可以忽略的;
假设2 接入策略是开放式接入,即所有用户都可以接入能为其提供最大瞬时接收信干比(signal and interference ratio,SIR)的基站.
假设3 用户和基站间信道为平坦瑞利衰落信道,路径损耗函数为l(x)=‖x‖-α,α>2.
图5和6分别为稀释前后两层异构蜂窝网系统基站分布图,其中最小距离R=0.3 km,λ2=4λ1.图5中MBS(Macrocell base station)为宏小区基站,FBS(Femtocell base station)为毫微微小区基站,图5中所有基站都是按照PPP模型分布的.图6中MBS按照MLPP模型分布,而FBS按照PPP模型分布.

图5 稀释前两层异构蜂窝网系统基站分布Figure 5 Distribution of two layers heterogeneous cellular system base station before dilution
由统计学知识[10-11]可知,对于随机分布的异构蜂窝系统来说,用户具有相同的统计特性,而与位置无关.因此,为了便于分析,本文考虑位于中央的用户,其接收信干比γ为


图6 稀释后两层异构蜂窝网系统基站分布Figure 6 Distribution of two layers heterogeneous cellular system base station after dilution

则Pc=P1+P2-P3就是用户的接入概率.
2.2 仿真性能分析
[8]设置仿真参数,假设对于一个大小为4×4=16 km2的异构蜂窝网系统,宏蜂窝基站功率为30 W,毫微微蜂窝基站功率为0.2 W,分布密度λ2=4λ1,最小距离R=0.3 km,毫微微蜂窝目标信干比为β2=0 d B.
2.2.1 接入概率
图7是两层都按照PPP模型和本文系统模型的接入概率仿真对比图.由图可以看出,MLPP模型在接入概率方面比PPP模型的性能更好.这是因为MLPP去除了距离过近的宏基站,使得干扰降低,接入概率上升.虽然性能的提升幅度不大,但对比图5和6可知整个系统中基站的数量约减少32%,这表明MLPP模型在资源更少的情况下得到了更好的性能,其系统效能也更高.
2.2.2 R的影响
R的大小决定MLPP的稀释程度,对MLPP中点的分布有很大的影响.R越大,基站保留概率越小,最终剩下的基站数量也越少,从而影响本文中两层异构蜂窝网的性能.注意到如果R值过大的话,剩下基站很少,这样会导致接入概率性能的下降.因此,寻找最合适的R值是分析研究和工程设计都需要解决的问题.
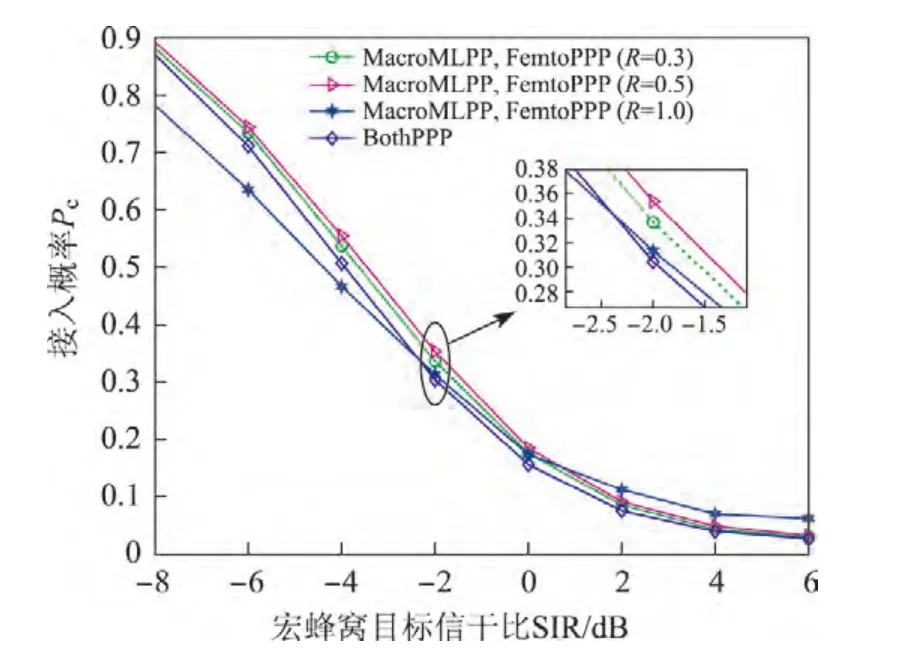
图8 不同稀释程度时接入概率的比较Figure 8 Access probability comparison for different dilution
目前蜂窝网中宏蜂窝和毫微微蜂窝基站的功率分别约为30 W和0.2 W,宏蜂窝基站的覆盖半径约为0.5~1.5 km.因此,本文对R∈[0.3,1.0]km,宏蜂窝和毫微微蜂窝基站的功率分别为30 W和0.2 W参数设置下的接入概率进行仿真,仿真结果如图7和8所示.图8表明:对于固定R,接入概率随着β1的增大而减小;对于某一固定β1值,不同R值对应的接入概率也不同,这一点结合图9可以说明.图9分别仿真了β1=4 dB,β2=0 dB和β1=-4 dB,β2=0 d B两种参数下接入概率与稀释半径R的关系.其中β1=4 d B,β2=0 d B时的接入概率随R的增大而增大,这是因为宏蜂窝目标SIR较大时,用户接收到宏基站的SIR很难满足较高的目标SIR,所以用户很难被宏蜂窝覆盖,接入概率主要由毫微微蜂窝覆盖的概率决定.宏蜂窝目标SIR较大时(β1>0 dB)不会出现因宏蜂窝剩余的基站数量过少而导致接入概率下降的情况,因为此时宏蜂窝的接入概率太小,决定系统接入概率的是毫微微蜂窝的接入概率.当β1=-4 d B,β2=0 d B时,接入概率随着R先增大后减小,R=0.6 km时接入概率最大,这是因为随着的R增大,距离过近的基站被移除,整个系统的干扰减小,接入概率上升;而当R增大到一定程度时,宏蜂窝剩余的基站数量过少导致接入概率下降.对于一个给定范围的多层异构蜂窝网,选定一个合适的稀释半径R,能获得最好的系统性能.在本文的仿真参数条件下,R=0.6 km是最合适的稀释半径.
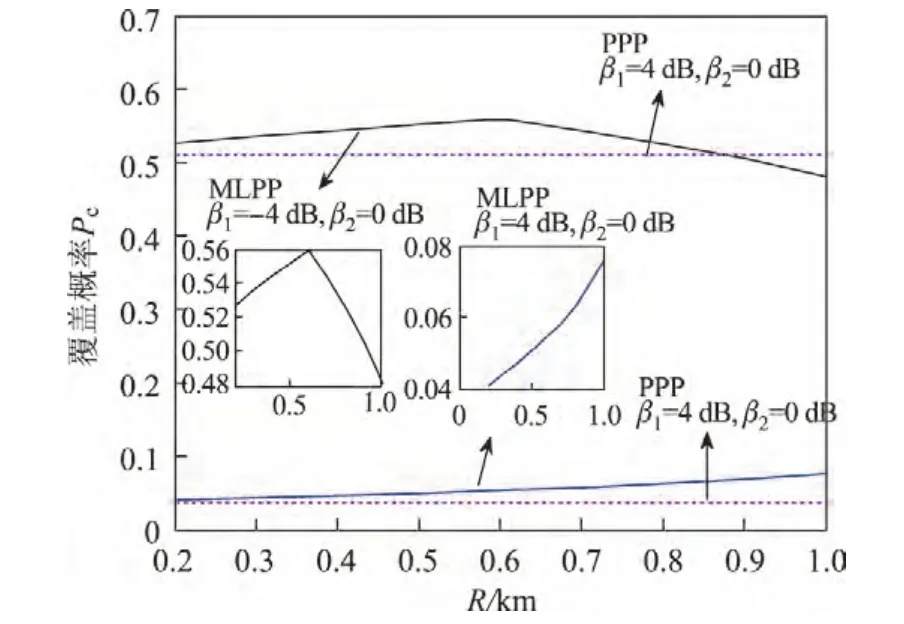
图9 宏蜂窝目标信干比不同情况下R的影响Figure 9 Access probability for different target SIR
2.2.3 系统效能
本文定义接入概率和所有基站总功率的比值(probability and total power ratio,PPR)为系统效能.图10给出了MLPP模型和PPP模型的系统效能在不同稀释半径R下的性能曲线.由图10可知PPR随着R的增大而增大,且当R=0.6 m时MLPP模型比PPP模型的PPR大约提升了60%,显著提高了系统效能,减少了资源开销,这是符合绿色通信的原则的.
综上所述,在建模分析异构蜂窝网时使用MLPP模型不仅在性能上能够超越使用传统的PPP模型,而且更符合实际的基站部署,同时还能在一定程度上提升系统效能,提高频谱利用率.可以说,本文所提模型是合理且有效的.
3 模型存在问题及改进

图10 不同R时系统效能Figure 10 PPR for different value of R
在前两个部分的分析和仿真中已经说明了MLPP模型的优点,但进行仿真研究时发现MLPP模型和PPP模型存在一个共同的缺点:很多用户接入宏蜂窝,很少接入到毫微微蜂窝.在实际的生活中,由于毫微微蜂窝具有方便、低接入代价和高QoS等优点,用户也愿意接入毫微微蜂窝.因此,本文引入一个偏好因子B[12],使得用户在多层异构蜂窝网的层选中更倾向于接入毫微微蜂窝.在这种偏好下,用户接入毫微微蜂窝的接收信干比为

当β1=β2=-2 d B时,采用不同偏移因子B的用户接入两种蜂窝网的比较结果如图11所示.图中用户只能接入宏蜂窝是指:网络范围内只存在使得用户接收信干比达到目标信干比的宏基站而不存在类似的毫微微基站能够满足用户的目标信干比.由图11可知,无偏移时用户接入毫微微蜂窝的概率大约只有接入宏蜂窝概率的1/10;当B=4时,用户接入毫微微蜂窝的概率大约为接入宏蜂窝概率的1/3.可知加入偏移可以明显地改善这种比例失衡的现象.
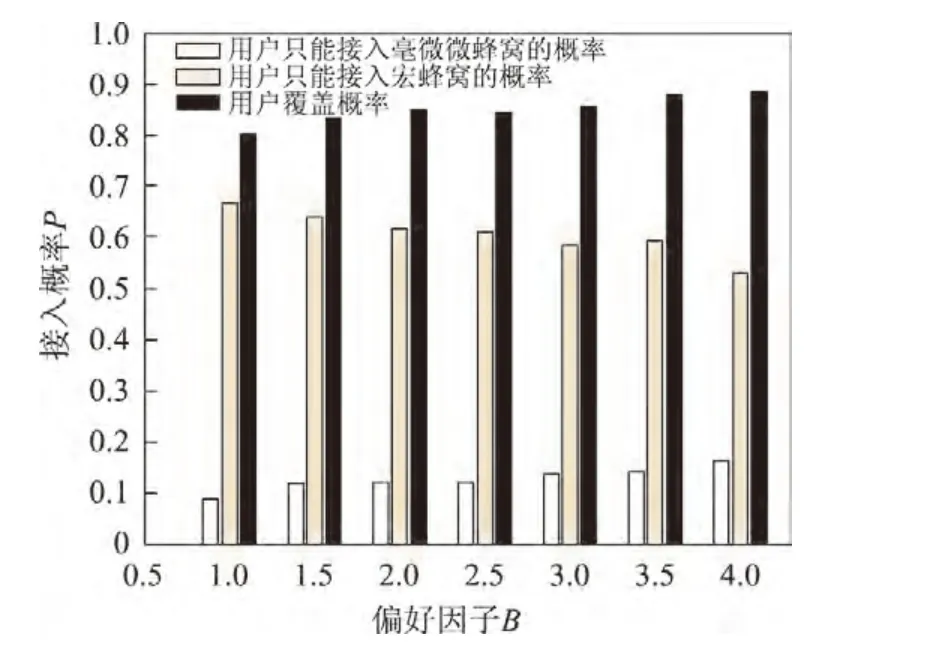
图11 用户接入两种蜂窝网的比较图Figure 11 Access probability comparison for different value of B
当实际用户接入时,用户接入毫微微蜂窝的代价费用低于接入宏蜂窝的代价费用,于是本文设计一个综合考虑信干比和接入代价的收益函数来描述网络的收益.假设用户对宏蜂窝的接入代价满意度[13]为

式中,xm表示接入宏蜂窝代价.假设用户在xm=0.2时的满意度为75%,则可求得αm=2.27,βm=0.12.
用户对毫微微蜂窝的接入代价满意度
式中,xf表示接入毫微微蜂窝代价.假设用户在xf=0.1时的满意度为75%,则可求得αf=4.53,βf=0.058.
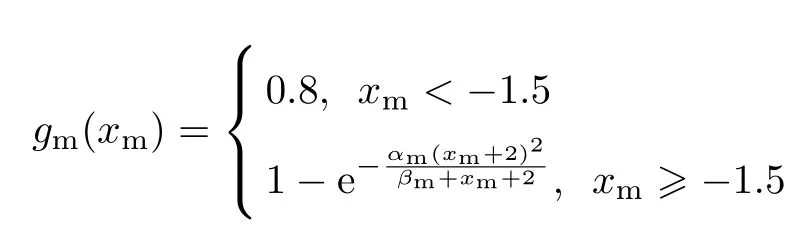
假设用户对接入宏蜂窝所能获得的接收信干比满意度为式中,xm表示接入宏蜂窝所能获得的接收信干比.假设用户在xm=0时的满意度为0.9,可求αm=0.95,βm=-0.35.
假设用户对接入毫微微蜂窝所能获得的接收信干比满意度为

式中,xf表示接入宏蜂窝所能获得的接收信干比.假设用户在xf=0时的满意度为0.9,可求得αf=0.52,βf=-0.42,则用户的总收益为A=af+bg,将f(x)、g(x)代入得
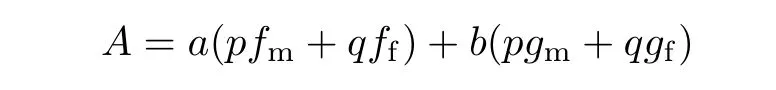
式中,p、q分别为用户接入宏蜂窝和毫微微蜂窝所占的比例,a、b分别为调节用户对接入代价和接收信干比的重视程度的参数.
图12所示为β1=0 dB,β2=2 dB时采用不同偏好因子用户的总收益仿真图,由图中a=0.8,b=0.2曲线可以看出,在没有偏好,即B=1时,用户的收益低至0.1;用户的总收益随着偏好因子B的增大而上升,当B增加到4时,用户的总收益约为0.9,此时用户总收益基本不再增加.相比于a=0.8,b=0.2时的曲线,a=b=0.5时的曲线初始值较高,但增长较慢,最大值也较小,这说明用户对接入代价较敏感.偏好因子的变化导致了毫微微蜂窝用户的变化,进而使接入到毫微微用户数量发生变化,因此用户总收益会随之变化.
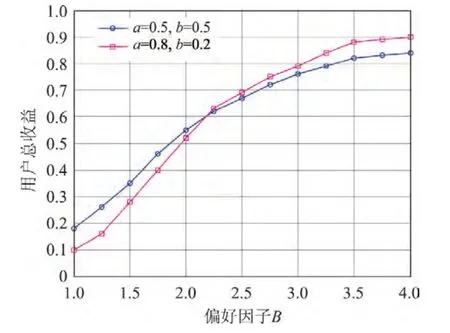
图12 不同偏好因子时用户总收益Figure 12 Total revenue of user versus the value of B
由图10和11可知,PPP模型和MLPP模型确实存在用户倾向于接入宏蜂窝的问题;加入偏好因子B后,这种现象得到明显的改观,且此时用户的总收益得到显著的提升.
4 结语
本文结合实际基站部署,指出常用的点过程模型存在的一些问题,引入了MLPP模型,并基于此模型仿真分析了包含宏蜂窝和毫微微蜂窝的两层异构蜂窝网的性能.结果显示,MLPP模型比传统的泊松点过程模型在接入概率方面性能更好,且使用的资源更少,MLPP模型的系统效能更高.本文在仿真分析中:发现在随机点过程模型下,由于点过程模型自身的缺陷,用户更倾向于接入发射功率大的宏蜂窝层.针对这个问题,本文引入一个偏好因子,使得网络负载得到均衡,并且仿真结果表明用户的收益增加,满意度上升.
参考文献:
[1]PARKVALL S,FURUSKARA,DAHLMANE.Evolution of LTE toward IMT-advanced[J].IEEE Communication Magazine,2011,49(2):84-91.
[2]LAGRANGE X.Multitier cell design[J].IEEE Communication Magazine,1997,35(8):60-64.
[3]CHANDRASEKHAR V,ANDREw S J,GATHERER A.Femtocell networks:a survey[J].IEEE Communication Magazine,2008,46(9):59-67.
[4]WYNER A.Shannon-theoretic approach to a Gaussian cellular multiple-access channel[J].IEEE Transactions on Information Theory,1994,40(6):1713-1727.
[5]JING S,TSE D,HOU J.Multi-cell downlink capacity with coordinated processing[C]//Proceedings of Information Theory and its Applications(ITA),San Diego,CA,2007.
[6]CATREUX S,DRIESSEN P,GREENSTEIN L.Simulation results for an interference-limited multiple-input multiple-output cellular system[J].IEEE Communication Letters,2000,4(11):334-336.
[7]ANDREw SJ,BACCELLIF,GANTIR.A tractable approach to coverage and rate in cellular networks[J].IEEE Transaction on Communications,2011,59(11):3122-3134.
[8]HARPREET S,GANTI R,BACCELLI F,ANEREw SJ.Modeling and analysis of K-tier downlink heterogeneous cellular networks[J].IEEE Journal on Selected Areas in Communications,2012,30(3):550-560.
[9]GANTIR.Stochastic geometry and wireless networks[M].Cambridge:Cambridge University Press,2012.
[10]STOYAN D,KENDALL W,MECKE J.Stochastic geometry and its applications[M].2nd ed.John Wiley and Sons,1996.
[11]BACCELLIF,BLASZCZYSZYNB.Stochastic geometry and wireless networks[M].Now:Foundations and Trends in Networking,2009.
[12]JO H,SANG Y,XIA P,ANDREw SJ.Outage probability for heterogeneous cellular networks with biased cell association[C]//IEEE Globecom,California,USA,2011.
[13]BOUAZIZA,KELIF J,DEABAT J.Analytical evaluation of LTE Femtocells capacity and indoor outdoor coexistence issues[C]//Proceedings of the 3rd European Wireless Technology Conference,London,2010.
