路面摩擦特性预测研究

孟令智，刘亚骄，杨震，郭卫卫

（长安大学汽车学院，陕西 西安 710064）

路面摩擦特性预测研究

孟令智，刘亚骄，杨震，郭卫卫

（长安大学汽车学院，陕西 西安 710064）

本次研究基于路面抗滑特性的预测问题，运用道路摩擦系数测试仪在公路上进行路面摩擦系数测试试验，并对试验结果进行分析，提出了路面摩擦系数的影响因素。应用广义回归神经网络分析方法，以影响因素为分类标准，确定了摩擦系数预测模型的分类，建立了基于广义回归神经网络的路面摩擦系数预测模型，并通过60组试验数据对网络模型进行了训练，利用6组实验数据进行预测结果对比。结果表明，模型预测值与实测值的平均误差为3.0%左右，模型预测结果与实测结果吻合，所构建模型是正确的，且具有较高的精度；此外还通过实车进行了汽车制动试验，并根据试验结果与模型预测结果对比，为交通事故分析中计算事故车速提供依据。

路面摩擦系数；试验；广义回归神经网络

CLC NO.:U461.51;U491.31Document Code:AArticle ID:1671-7988(2014)02-33-05

前言

改革开放以来，我国经济快速发展，公路建设里程大幅增长，人均汽车保有量也快速增加，伴随着交通事故数量呈上升趋势。在交通事故鉴定分析过程中，路面摩擦系数可以为交通事故分析提供重要依据[1-2]，因此，研究关于路面摩擦特性的预测具有重要意义[3-5]。

关于路面摩擦系数的预测研究，可以把路面摩擦系数的预测方法分为三类：经典预测方法（经验法、力学法）、传统预测方法（回归分析法、时间序列法[6]）、现代预测方法（模糊预测法[7]、灰色预测法[8]）等。这些方法大都集中在对其因果关系回归模型和时间序列模型的分析上，所建立的模型不能全面地反映所预测的动态数据的内在结构和复杂性，影响了预测精度。本文通过用道路摩擦系数测试仪进行试验，采集若干数据，对这些数据进行分析处理的基础上，建立基于广义回归神经网络的路面摩擦系数预测模型，介绍路面摩擦系数的预测方法。

1、试验及数据处理

试验选取西安地区公路作为试验路段，在各种不同状况下的路面上进行路面摩擦系数测试试验。研究中所用仪器为道路摩擦系数测试仪。试验时，在道路上选取一个测点，测点位置与路面边缘距离大于1米，将仪器置于测点上并使仪器移动方向与车辆行驶方向一致，匀速拖动测块，且拖动距离不小于1米，拖动时间大于5秒，每个测点重复测试6次。测点分布如表1所示，部分试验统计结果如表2所示。

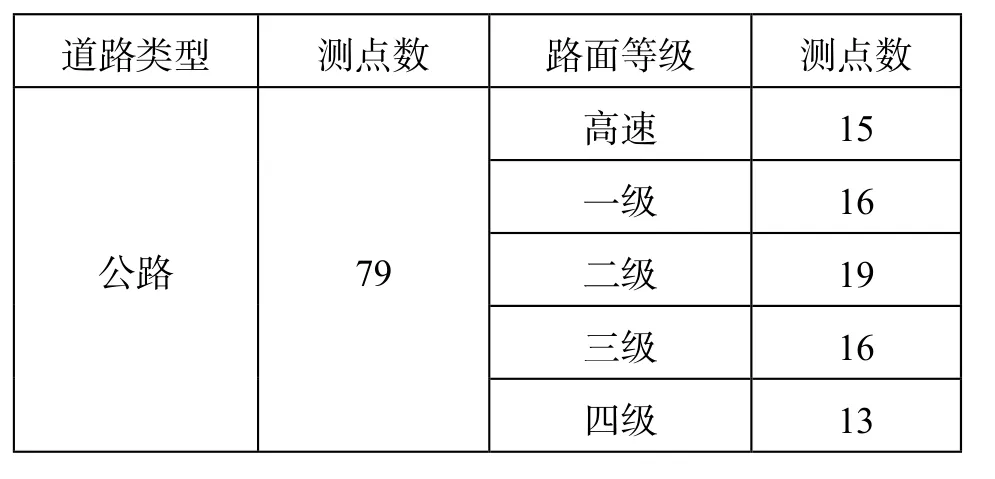
表1 试验测点分布

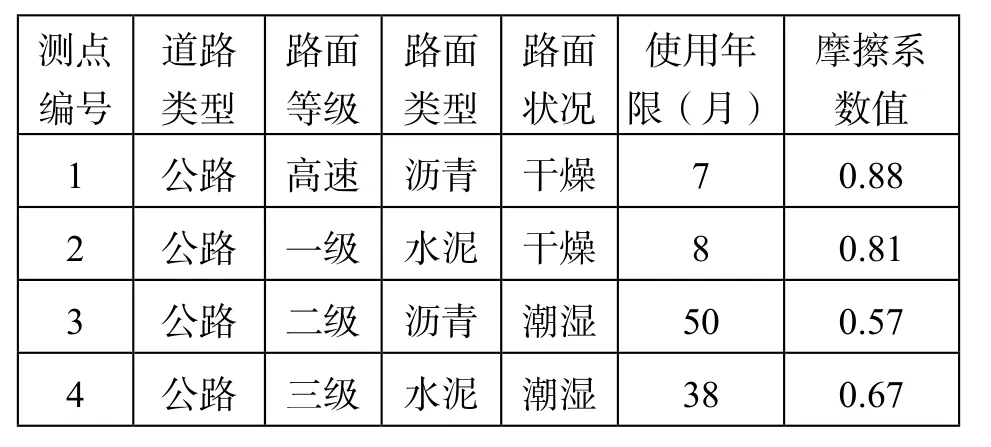
表2 摩擦系数数据统计

从79个测点测量结果可以看出，路面摩擦系数的大小与下列因素有关：

（1）路面等级，高等级路面的摩擦系数显著高于低等级路面的摩擦系数，高等级路面主要是高速公路、一级公路等。低等级路面主要有二级公路、三级公路等。

（2）使用年限，相同的路面，随着使用时间的增加，路面摩擦系数值降低。

（3）路面状况，路面摩擦系数随着路面状况由高到底的排序为：干燥﹥潮湿﹥积水。

（4）路面类型，由于路面材料的不同，摩擦系数值也有一定的差异。

2、基于广义回归神经网络的路面摩擦系数预测模型

2.1 广义回归神经网络

广义回归神经网络是一种径向基神经网络，其适用于解决非线性问题，它具有较强的非线性映射能力和柔性网络结构，此外还具有较高的容错性和鲁棒性，以及良好的逼近能力、分类能力和快速的学习能力。

GRNN在结构上由四层构成，分别为输入层、模式层、求和层、输出层。对应的网络输入其网络输出为如图1所示。

GRNN结构具体描述如下：

（1）输入层神经元数目等于学习样本中输入向量的维数m，各神经元是简单的分布单元，直接将输入变量传递给模式层。

因而对于GRNN，一旦确定了训练样本，那么网络结构以及各神经元之间的连接权值也随之确定，影响网络输出的唯一因素是光滑因子σ。从而网络的学习完全依赖于样本数据，可最大程度地避免人为主观假定对预测结果的影响。并且GRNN根据样本数据逼近其中隐含的映射关系，甚至在样本数据少时网络的输出结果也能够收敛于最优回归表面，而且在结构方面也具有高度的并行性，从而可以大大提高网络的训练速度，能改善拟合的精度。

2.2 预测模型建立

根据路面类型、路面等级、路面状况等三个影响因素对摩擦系数预测模型划分成6类，各种类型预测模型的训练样本与预测样本数如表3所示，各种预测模型总共利用试验数据60组，其中预测数据有6组。

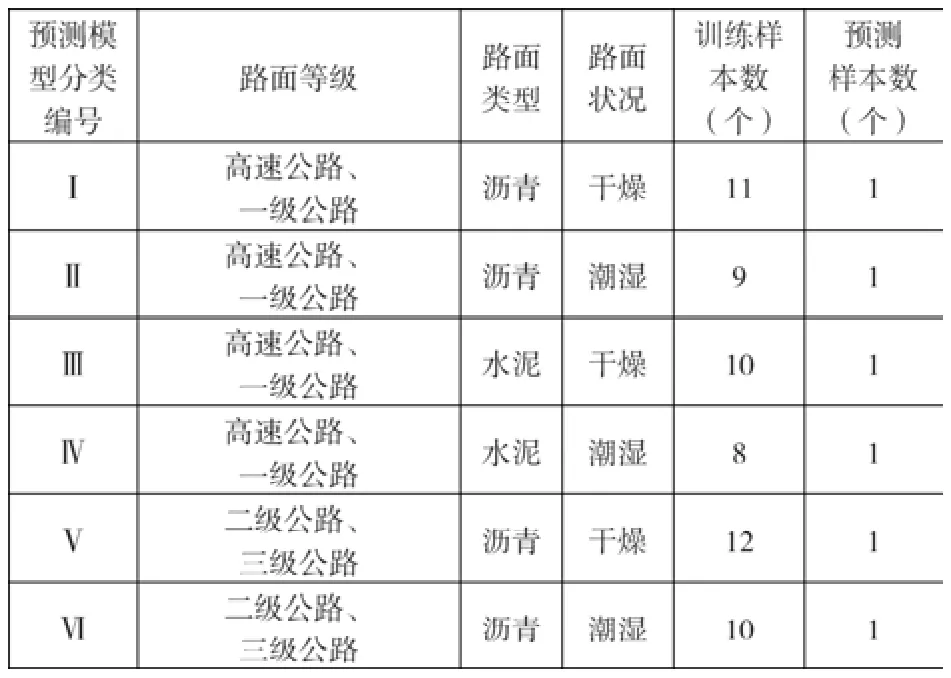
表3 各种类型预测模型训练样本与预测样本数

根据对路面摩擦系数影响因素的分析，本文采用使用年限为网络输入层，路面摩擦系数为网络输出层，建立基于广义回归神经网络的路面摩擦系数预测模型，如图2所示。

3、模型预测

3.1 光滑因子优化

在Matlab下编制程序，模型采用4次交叉验证，使用网络训练样本。网络分布密度在[0.01,1]区间内以0.01为步长，选用不同σ值进行训练，得到光滑因子出现最优值时光滑因子最优时对应的最小误差，如表4所示。

表4 各类预测模型光滑因子最优时对应的最小均方误差

3.2 预测结果分析

通过建立神经网络预测模型，利用60组训练样本经过网络训练后，用6组预测样本最终得到预测结果并与实测值进行结果比对。如表5为摩擦系数预测结果对比。

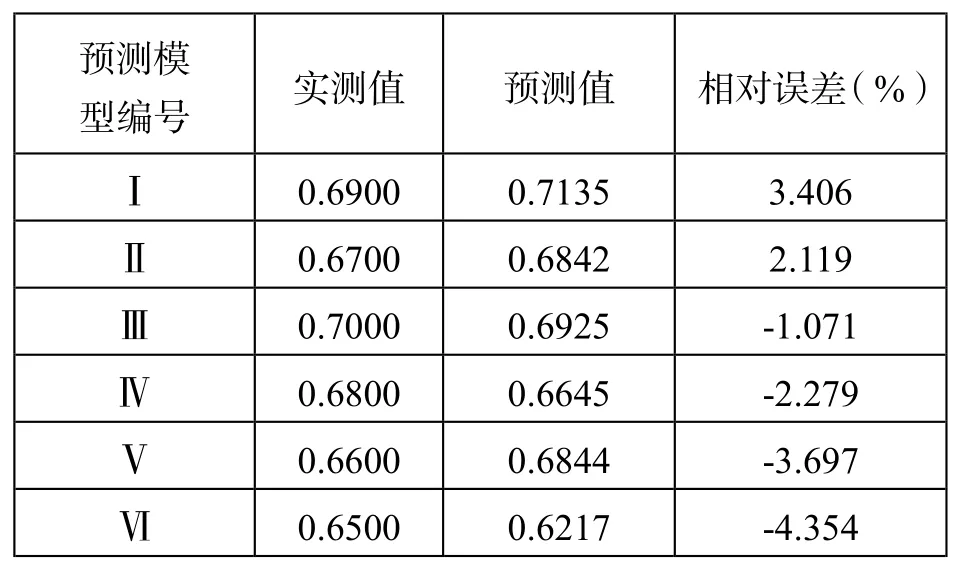
表5 摩擦系数预测结果对比

基于广义回归神经网络摩擦系数预测模型的预测值与实测值基本接近，模型也有很好的稳定性。预测摩擦系数最小相对误差和最大相对误差分别为1.071%、4.354%，模型有较高的预测精度。证明基于广义回归神经网络的摩擦系数预测模型在摩擦系数预测中是有效的。

4、实车验证及应用

本文利用SG-630型便携式制动性能测试仪在上述六种预测模型路面状况上进行汽车制动性能试验，来探究在汽车制动过程中利用的纵向附着系数φS与预测模型预测的路面摩擦系数μJ之间的关系，为在交通事故分析中应用广义回归神经网络预测路面摩擦系数来分析事故车速提供重要依据。

利用SG-630便携式制动性能测试仪可得到汽车在制动过程中制动距离和制动初速（如表6所示），汽车制动过程中制动距离、制动前车辆速度、纵向附着系数φS、制动减速度、制动力F等的关系为：

式中：N—为汽车车轮作用在路面上的正压力，可把N近似为N=mg；m—为汽车的质量；v1—为制动初速度；s—制动距离；v2—为制动末速度，v2=0。

变换得到汽车制动过程中纵向附着系数Sφ为：

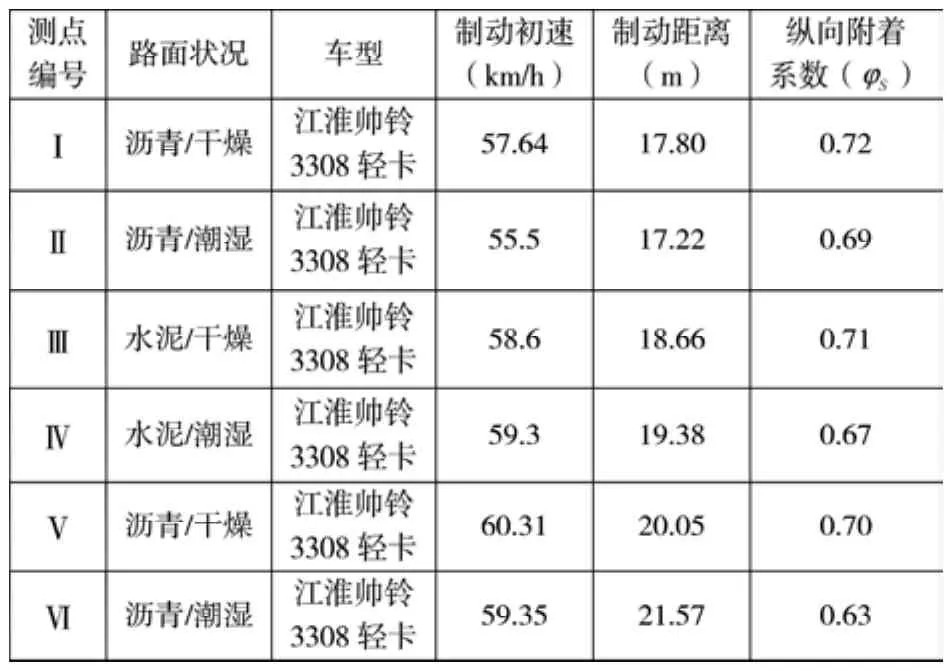
表6 汽车制动试验测试结果

假定摩擦系数Jμ与纵向附着系数Sφ存在关系：

得到对比测试中k的结果如表7所示。

表7 k值结果

5、结论

（1）对试验数据进行分析，提出路面摩擦系数的影响因素。

（2）以影响因素为分类基础，确定摩擦系数预测模型分类及输入参量；应用广义回归神经网络分析方法，建立基于广义回归神经网络的路面摩擦系数预测模型。

（3）广义回归神经网络预测方法是一种有效的摩擦系数预测方法。

[1] 杨圣文.道路交通事故车速鉴定分析方法研究[D].西安：长安大学，2006.

[2] 蒋柯.道路交通事故车速鉴定规范化研究[D].西安：长安大学，2010.

[3] 孙明哲,裴玉龙.道路摩擦系数测定方法若干问题的讨论[J].黑龙江交通科技，2004，128(10):78-79.

[4] 王利利.路面抗滑性能变化特性研究[D].北京工业大学，2008.

[5] 孙荣山.路面管理系统使用性能预测模型研究[D].北京工业大学,2004.

[6] 倪富健,方昱,薛智敏.时间序列在路面平整度预测中的应用.东南大学学报(自然科学版)，2006,(4):634-637.

[7] 陈涛,张淼,魏朗. 基于预瞄的山区高速公路驾驶人车速模糊控制模型[J]. 北京理工大学学报,2012,32(增刊1):51-54.

[8] 王国晓,安景峰,陈荣生．灰色理论在路面使用性能中的应用[J].公路交通科技,2002，19(3):16-19.

The research of road friction properties’ prediction

Meng Lingzhi, Liu Yajiao, Yang zhen, Guo Weiwei

（Chang’an University, Shaanxi Xi’an 710064）

In order to study the problem of road friction properties’s prediction, the test of measuring road friction coefficient was carried. Road friction coefficient tests were carried through road friction coefficient tester, and the impact fact of road friction coefficient was obtained. By the General Regression Neural Network，the prediction model of road friction coefficient was established based on road influence factor. The network model was trained through 60 test data, and the contrast between the predicted results and the measured test results was done through 6 test data in network model. The results show that the average error between the predicted results and the measured test results is 3.0%, the model’s predicted results are consistent with the measured test results, the model which was set established in this article is correct and has a high accuracy, in addition, auto braking test was carried by the real car, through the contrast of two results, basis was raised for traffic accident analysis when speed of accident was calculated.

road friction coefficient; test; GRNN Network; prediction model

U461.51；U491.31

A

1671-7988(2014)02-33-05

孟令智，硕士研究生，就读于长安大学。