GPS坐标时间序列共模误差空间特性分析

谢树明，潘鹏飞,，周晓慧

（1. 武汉市测绘研究院, 湖北 武汉 430022；2. 武汉大学 测绘学院，湖北 武汉 430079）

近20 a累积的全球GPS参考站坐标时间序列为大地测量学及地球动力学研究提供了宝贵的数据基础。然而，GPS数据处理过程受众多因素的影响，所得GPS坐标时间序列中难免存在多种误差[1-3]。Wdowinski对区域GPS网站点坐标时间序列分析发现，区域GPS网内不同站点坐标时间序列受到共模误差（common mode error）的影响[4]。杨国华等研究表明，共模误差可能是GPS单日解的主要误差源[5-10]。由于共模误差的起源尚不明了，目前只能利用某种形式的空间滤波计算共模大小[3,11]。研究共模误差的空间特性有利于分析其来源，并在观测数据解算阶段将其剔除，有效提高GPS成果的精度。

1 共模误差的计算方法

1.1 区域叠加滤波

区域叠加滤波法是目前广泛采用的提取共模误差的方法。假设共模误差在某一区域均匀分布，将单日解误差作为权重因子，则[8]：

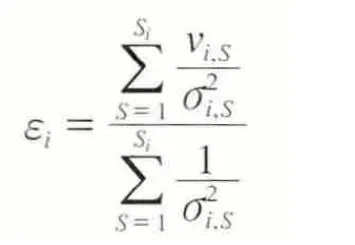
其中，εi为第i个台站的共模误差值；v为残差坐标时间序列；σi,S为单日坐标解的误差；S为参与计算共模误差的站台数。

1.2 相关系数加权叠加滤波

相关系数加权叠加滤波算法引入相关系数作为权重因子，并以某一个基准站为单位，计算所有测站对其产生的共模误差的大小：

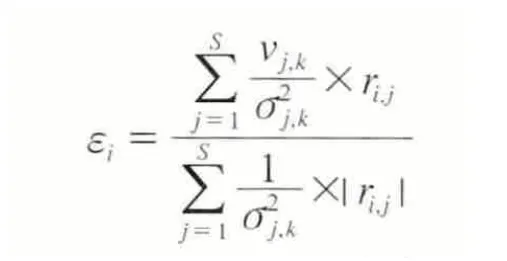
其中，εi为第i个台站的共模误差值；S为参与计算共模误差的台站数；vj,k和σ2j,k分别为第j个台站某一位置分量第k天的残差和误差；ri,j为站i和站j该分量残差坐标时间序列间的相关系数。

2 基准站空间分布的影响

2.1 基准站的聚类分析

本文利用相关系数能够表示坐标时间序列间相关性的特点，把相关系数作为指标，提取坐标时间序列相关性显著的基准站，分析共模误差的空间特性。GPS基准站坐标间的相关系数rxy的计算基于两个基准站坐标分量的残差时间序列（x和y）的公共历元进行：

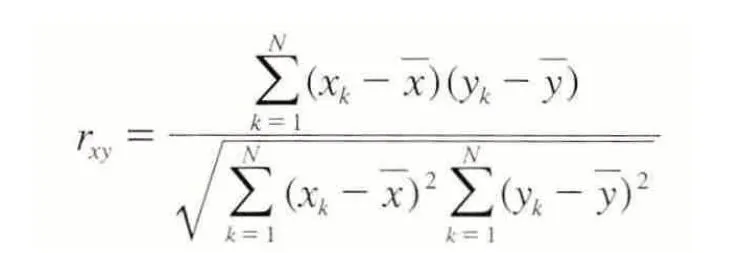
其中，N为公共历元的个数；和为两个GPS基准站残差坐标时间序列的均值。

本文以WUHN站为例，分别计算WUHN基准站水平方向和垂直方向残差坐标时间序列与全球138个IGS基准站之间的相关系数，并选取水平方向和垂直方向相关系数大于0.2的基准站。结果表明，测站间距离较短时，水平方向相关系数显著，且测站运动方向基本相同；而垂直方向相关系数受测站之间纬度差影响较大，与距离之间的关系不明显。例如，YSSK站与WUHN站相距约3 100 km，而纬度仅相差16.498°，垂直方向相关系数为0.248；而IRKT基准站与WUHN站相距约2 500 km，且纬度相差21.69°，N、E、U方向相关系数分别为0.31、0.31及0.16。因此，测站之间的距离及板块运动方向是影响水平方向坐标时间序列共模误差的因素，纬度之差是影响垂直方向坐标时间序列共模误差的因素。

2.2 GPS网空间尺度的影响

本文采用相关系数加权叠加滤波计算不同空间尺度GPS网中共模误差的大小。以WUHN站为例，分别计算了1 000 km范围内9个IGS站及全球范围138个IGS站对其产生的共模误差。如图1所示，蓝色表示1 000 km范围GPS网相关系数叠加滤波后WUHN基准站的共模误差，红色表示全球范围GPS网相关系数叠加滤波后WUHN基准站的共模误差。可以看到，1 000 km范围GPS网的滤波后水平方向共模误差在-10 mm～10 mm之间，最不利的情况下会达到±30 mm，垂直方向共模误差在-20 mm～20 mm之间。而全球范围的滤波结果中，水平方向共模误差范围在-2 mm～2 mm之间，垂直方向共模误差的 范围在-5 mm～5 mm之间。同一个IGS基准站由于选择不同空间尺度的GPS网进行相关系数叠加滤波，计算得到的共模误差会存在较大的差异。

2.3 GPS基准站密度的影响

基于全球138个IGS站相关系数叠加滤波的结果，分别求出每个基准站共模误差时间序列的标准差。结果表明，各地IGS基准站共模误差的离散程度存在明显差别，南美洲IGS站共模误差的离散度最大，北美洲和欧洲等地IGS站共模误差的离散度最小，这种分布趋势与基准站的分布密度相一致。基准站越密集的地区，共模误差的离散程度越小，表明共模误差受GPS基准站分布密度的影响。

3 负相关测站之间共模误差的分析

当测站之间的距离达到数千km甚至上万km时，部分测站坐标时间序列间的正相关性不再明显，甚至呈现出显著的负相关性。本文选取与WUHN站N方向残差坐标时间序列相关系数最小的7个基准站进行分析。对以上8个IGS基准站N方向残差坐标时间序列进行相关系数加权叠加滤波，滤波前后与WUHN站的相关系数如表1所示。

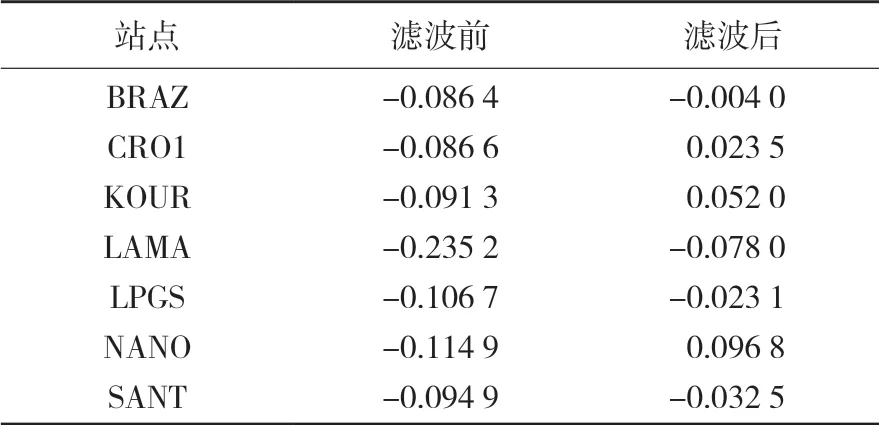
表1 滤波前后测站之间相关系数

从表1可以看出，通过相关系数加权叠加滤波以后，7个测站与WUHN站的相关性都有不同程度的减弱。例如，BRAZ站与WUHN站滤波前的相关系数达到 -0.086 4，滤波后仅为-0.004 0；而LAMA站与WUHN站滤波前的相关系数达到-0.235 2，滤波后仅为-0.078。以上结果表明，负相关的GPS测站中仍然存在共模误差，而采用相关系数加权叠加滤波能够剔除共模误差，降低测站之间的负相关性。

[1]李昭，姜卫平，刘鸿飞，等.中国区域 IGS 基准站坐标时间序列噪声模型建立与分析[J].测绘学报，2012, 41(4): 496-503

[2]黄立人.GPS 基准站坐标分量时间序列的噪声特性分析[J].大地测量与地球动力学，2006, 26(2): 31-34

[3]Mao A, Harrison C G, Dixon T H. Noise in GPS Coordinate Time Series[J].Journal of Geophysical Research: Solid Earth(1978–2012)，1999, 104(B2): 2 797-2 816

[4]Wdowinski S, Bock Y, Zhang J, et al. Southern California Permanent GPS Geodetic Array: Spatial Filtering of Daily Positions for Estimating Coseismic and Postseismic Displacements Induced by the 1992 Landers Earthquake[J].Journal of Geophysical Research: Solid Earth (1978–2012)，1997,102(B8): 18 057-18 070

[5]杨国华，汪翠枝，杨博，等. ITRF框架对GPS连续观测的影响研究[J].大地测量与地球动力学，2009, 29(4): 5-9

[6]袁林果，丁晓利，陈武，等. 香港 GPS 基准站坐标序列特征分析[J]. 地球物理学报，2008, 51(5): 1 372-1 384

[7]Dong D, Fang P, Bock Y, et al. Spatiotemporal Filtering Using Principal Component Analysis and Karhunen‐Loeve Expansion Approaches for Regional GPS Network Analysis[J]. Journal of Geophysical Research: Solid Earth (1978–2012)，2006,111(B3)：3 405-3 421

[8]Williams S D, Bock Y, Fang P, et al. Error Analysis of Continuous GPS Position Time Series[J]. Journal of Geophysical Research:Solid Earth (1978–2012)， 2004, 109(B3)：3 412-3 431

[9]田云锋，沈正康，李鹏. 连续 GPS 观测中的相关噪声分析[J].地震学报，2010, 32(6): 696-704

[10]田云锋，沈正康. GPS 坐标时间序列中非构造噪声的剔除方法研究进展[J].地震学报，2009, 31(1): 68-81

[11]Nikolaidis R. Observation of Geodetic and Seismic Deformation with the Global Positioning System[D]. University of California,2002