计及热效应的小展弦比机翼气弹稳定性分析＊

赵 卫， 韩晓林， 费庆国

（1.东南大学土木工程学院 南京，210096） （2.东南大学江苏省工程力学分析重点实验室 南京，210096）

引 言

随着高／超声速飞行器的发展，高／超声速气流引起气动加热产生的热问题越来越受到重视。结构在热环境下的动力学问题是发展高／超声速航天飞行器面临的重要课题。20世纪50年代末至60年代初，美国对热气动弹性问题的研究出现了一个高潮，这些研究为之后航天飞机的设计打下了坚实的基础［1］。Garrick［2］综述了热气动弹性力学的发展，在传统气弹力三角形的基础上补充了由热效应引起的作用力，提出了一种新的描述热气动弹性力学各学科关系的四面体关系图。随着计算机运行能力的提高和计算流体动力学（computational fluid dynamics，简称CFD）的发展，气动加热的计算精度和效率得到很大提高，为结构在热环境中的动力特性分析提供了准确的“温度载荷”。在结构和气动力耦合方面，Krist等［3］基于RANS方程开发了CFL3D求解器，为基于CFD的高／超声速飞行器的结构气弹稳定性分析提供了有效工具。由于CFL3D能够准确模拟非定常气动力，McNamara等［1，4］基于 CFL3D分析了超声速气流中气动弹性稳定性，并取得了一定的进展。20世纪90年代初，美国开展了NASP（25倍马赫数）、TAV，Hy－Tech，Hyper－X等飞行器研究，为热气弹分析提供了大量的实验数据［5-6］。Heeg等［7］针对 NASP 验证模型提出了热气动弹性分析的5个步骤，但其并没有考虑热应力引起的附加刚度。针对热效应对结构振动特性的影响，史晓明等［8-9］研究了变厚度弹翼的热动力学特性，对比有限元分析和实验结果，发现结构前3阶固有频率较常温均有所下降。在热气动弹性数值计算方面，吴志刚等［10-11］提出了分层求解的思想，采用分开建立方程的松耦合解决方案，即分别进行气动加热计算、结构温度场分析、热模态分析、气动弹性分析，在一个时间步上顺序求解，从而使问题简化。基于此分层求解思想，文献［10］分析了高／超声速稳态热环境下翼面的结构、气动和热的耦合动力学问题，采用单向耦合方法进行计算，发现受热结构的动力特性和颤振特性均可能发生变化，尤其是对于根部固支翼面。

笔者以小展弦比机翼作为研究对象，根部完全固支，探索其在高／超声速气流的瞬态热环境下的动力学特性和气弹稳定性，考虑了热应力引起的刚度效应，研究热应力对结构刚度的影响，利用活塞理论计算非定常气动力，采用p－k法求解气弹方程［12-15］，分析讨论热效应对结构振动特性及颤振边界的影响，同时还研究了不同边界约束条件下热应力对结构振动特性和气弹稳定性的影响。

1 有限元模型

小展弦比机翼根部弦长和尖部弦长分别为1.0m和0.3m，展长为0.4m，前缘后掠角为33.7°，机翼根部完全固支。有限元模型［16］如图1所示。

材料为超硬铝合金7075－Al，该型号铝合金材主要用于制造飞机结构及要求强度高、抗腐蚀性强的高应力构件。假定材料密度不随温度变化，ρ＝2 750kg／m3，泊松比μ＝0.3。其他材料结构参数和热特性参数随温度变化如表1所示。

表1 不同温度下7075－Al材料参数Tab.1 Material properties of 7051－Al at differnet temperature

图1 小展弦比机翼有限元模型示意图Fig.1 Finit element model of low aspectration wing

2 瞬态温度场分析

2.1 温度场分布方程

三维瞬态温度场在直角坐标系下满足微分方程

当一个方向上（若为z方向）温度变化为零时，方程就为二维问题的热传导方程

若只有z方向有温度变化，则方程为一维热传导方程

其中：kx，ky，kz分别为材料沿x，y，z方向的热传导系数；φ为瞬态温度场的场变量φ（x，y，z，t）；ρ为大气密度；c为比热；Q为内部热源。

笔者假设机翼沿厚度方向的温度分布变化为0，即z向无温度梯度，同时机翼内部不产生内源，则式（2）可写成

2.2 瞬态温度场分析

利用式（4）计算翼面温度分布。本研究中“热源”为热流密度，假设机翼前缘的热流密度为1.0×105W／m2，考虑空气对流的影响，对流传热系数h＝10.0W／m2°C，环境温度为20°C，选取50，500，1 000，2 000和3 000s时段的温度视为“温度载荷”进行结构模态分析和颤振分析，分析不同时刻下的频率和颤振边界，并探讨其变化规律。

3 热模态分析

热效应对结构振动特性的影响主要是改变结构总体刚度。温度对结构刚度的影响主要表现在两个方面：a.高温下结构材料性能发生退化，直接降低了结构刚度；b.不均匀的温度场使结构产生热变形，热变形在外界约束条件下会在结构内部产生预拉或预压应力，或二者同时存在，使结构发生硬化或软化。为此，热环境下结构刚度矩阵包含原刚度阵受温度变化影响后的值KT和附加的应力刚度Kσ，即

忽略结构阻尼的影响，考虑热效应的结构振动方程为

其中：M为结构的质量矩阵；ω为结构的固有频率；φ为结构的模态振型。

对两种工况进行分析：工况1为同时考虑热应力引起的附加刚度及材料特性退化引起结构刚度的下降；工况2为只考虑材料特性的退化引起结构刚度的下降。

热模态分析分为两步：a.加载给定加热时刻下的“温度载荷”，更新刚度矩阵，选中存储每一步的刚度矩阵；b.调用修正后的刚度矩阵进行模态计算。利用SOL 106求解器分析不同时刻温度载荷下的应力，选中“正则化模态分析”选项进行模态分析，其结构固有频率如表2所示。对应的前4阶常温模态如图2所示，常温模态频率与文献［16］中的数据相符。由表2可知，加热到3ks时，前4阶固有频率较常温下降了9.4%，17.3%，12.9%和4.5%，其中扭转模态（第2阶和第3阶模态）频率下降比较大。

表2 不同温度载荷下机翼的固有频率（工况1）Tab.2 Model frequencies at different temperature loads（case 1） Hz

图2 常温下机翼前4阶模态振型图Fig.2 Mode shapes of the first 4modes

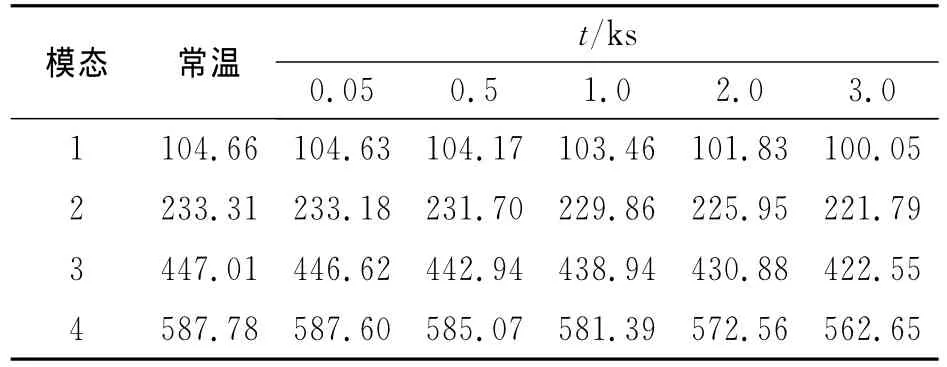
表3 不同温度载荷下机翼的固有频率（工况2）Tab.3 Natural frequencies of the first 4modes at different temperature loads（case 2） Hz

忽略热应力引起的附加刚度效应时，固有频率在不同时刻温度载荷下的数据如表3所示。由表3可知，该工况下翼面加热到3ks时，前4阶固有频率较常温时下降了4.4%，4.9%，5.5%和4.3%。

对比两种工况下的频率变化曲线见图3。只考虑材料退化对结构刚度的影响时，结构各阶固有频率随着气动加热的进行一直降低。当考虑热应力的变化产生附加刚度时，热效应在气动加热初期提高了结构固有频率，表明此时热应力的变化增大了结构的总体刚度；但随着气动加热的进行，热应力的引入在很大程度上降低了结构总体刚度，特别是对扭转刚度的影响很大，如图3中的第2、第3支模态。

图3 热效应对结构固有频率的影响Fig.3 Influences of thermal effect to the natural frequencies

4 颤振计算

4.1 气弹运动方程

在超声速、高超声速非定常气动力的计算中，活塞理论能很好地满足工程精度的要求［14］。活塞理论是一种无粘非定常气动理论，同时也是一种简化的气动力理论，只适用于在超声速气流下对机翼进行颤振分析。实验证明，马赫数在2～5之间，用这种理论对超声速翼面计算都能得到满足精度要求的结果［12-14］。

在等熵条件下由动量方程可得

由于活塞前进速度｜v｜≪c∞，故有｜v／c∞｜≪1，上式展开后则可略去高阶微分项。当只保留一阶项时，称为一阶活塞理论，即为

当保留二阶项时，可得到二阶活塞理论，即

作用在机翼表面上的压力分布可得到上、下表面的压力差为

对于本研究中的均匀厚度机翼，此时厚度效应为零，则上、下翼面压力差

在热环境下，热气动弹性颤振方程［10］为

Kj包括热应力引起的附加刚度，其结果可由式（5）计算可得。针对方程（12），采用p－k法求解，即给定一系列速度，反复迭代求解颤振数据。

4.2 飞行环境

气流马赫数为3.0，空气密度ρ＝1.226kg／m3，飞行高度为海平面，空气密度比为1.0，机翼攻角为0°。结构单元为实体单元，气动网格点的位移和力通过无限板样条方法插值到结构单元上，在NASTRAN中采用p－k法进行气弹分析［15］。

4.3 结果分析

沿用热模态分析中的两种工况，工况1下，结构在超声速气流中的颤振边界如表4所示。与常温下的颤振边界相比，气动加热到3ks时，颤振速度和颤振频率较常温时下降了33.67%和26.49%。工况2下，颤振边界如表5所示。相比较而言，忽略热应力的影响时，3ks时段的颤振速度和颤振频率较常温时下降了5.11%和6.40%，与表3中固有频率的下降幅度非常接近。

图4反应出热应力的引入对结构颤振边界的影响是很大的，尽管加热初期热应力提高了固有频率，增大了颤振速度和颤振频率，但随着气动加热的进行，热应力却在很大程度上降低了颤振边界，相比只有材料性能退化对颤振边界的影响下降很多。

表4 不同温度载荷下的颤振边界（工况1）Tab.4 Flutter boundaries of the wing at different temperature loads（case 1）

表5 不同温度载荷下的颤振边界（工况2）Tab.5 Flutter boundaries of the wing at different temperature loads（case 2）

为了进一步探讨热应力的变化对颤振边界的影响，笔者考虑了另外一种边界约束条件下的颤振边界，在根部弦处（0.2，0，0）和（0.8，0，0）两点处固支，其对应的颤振边界如表6所示。

表6 不同温度载荷下的颤振边界（两点约束）Tab.6 Flutter boundaries of the wing under two－node fixed boundary conditions

图4 热效应对颤振特性的影响Fig.4 Influence of thermal effect to the flutter boundary

分析表6中的颤振数据，在边界约束较少的情况下，其颤振边界在气动加热初期也得到了提高。随着气动加热的进行，颤振速度和颤振频率较常温时下降了11.72%和12.76%。对比机翼两种边界约束条件下分别在两种工况下的颤振边界曲线，如图5所示。从图中可以看出，边界约束越少，热应力的变化对结构颤振边界的影响也越小。

5 结 论

1）高温导致结构材料特性的退化直接减小原始结构刚度，降低结构固有频率。

2）热应力的引入在气动加热初期提高了结构各阶固有频率，然而随着气动加热的进行，热应力却在很大程度上降低了其各阶固有频率，其中扭转模态频率下降最为严重。

3）只考虑材料退化对结构刚度的影响时，颤振边界的下降程度与固有频率的下降程度接近。

图5 不同边界两种工况颤振边界曲线Fig.5 Flutter boundaries under two different boundary conditions

4）不同的边界约束条件下热应力的分布是不同的，边界约束越小，热应力的变化也会越小，其对结构刚度的影响程度也越小；反之，影响会变大。

5）在翼面温度分布趋向于稳态的过程中，颤振边界伴随着气动加热的进行不断发生变化，不同结构边界约束条件下，热应力在气动加热初期均提高了颤振速度和颤振频率，但最终都在很大程度上降低了颤振速度和颤振频率。因此在高／超声速飞行器设计过程中，必须要考虑由于气动加热引起的热效应对结构振动特性和气动弹性稳定性的影响，确保飞行器的飞行安全。

［1］ McNamara J J，Thuruthimattam B J，Friedmann P P，et al.Hypersonic aerothermoelastic studies for reusable launch vehicles［C］∥45thAIAA／ASME／ASCE／AHS／ASC Structures，Structural Dynamic ＆ Materials Conference.Palm Springs，California：AIAA，2004：1－35.

［2］ Garrick I E.A survey of aerothermoelasticity［J］.Aerospace Engineering，1963，22（1）：140－147.

［3］ Krist S L，Biedron R T，Rumsey C L.CFL3Duser′s manual（version 5.0）［R］.［S.l.］：NASA，1998.

［4］ Friedmann P P，McNamara J J，Thuruthimattam B J，et al.Aeroelastic analysis of hypersonic vehicles［J］.Journal of Fluids and Structures，2004，19：681－712.

［5］ Jack J M，Peretz P F，Kenneth G P，et al.Three－dimensional aeroelasticity and aerothermoelastic behavior in hypersonic flow［C］∥Proceedings of 46thAIAA／ASME／ASCE／AHS／ASC Structures，Structural Dynamics ＆ Materials Conference. Austin，Texas：AIAA，2005：1－47.

［6］ McNamara J J.Aeroelastic and aerothermoelastic behavior of two and three dimensional lifting surface in hypersonic flow［D］.PH.D Thesis：The University of Michigan，2005.

［7］ Heeg J，Zeiler T A，Pototzky A S，et al.Aerothermoelastic analysis of a NASP demonstrator model［R］.［S.l.］：NASA，1993.

［8］ 史晓明，杨炳渊.瞬态加热环境下变厚度板温度场及热模态分析［J］.计算机辅助工程，2006，15（S）：15－18.

Shi Xiaoming，Yang Bingyuan.Temperature field and mode analysis of flat plate with thermal environment of transient heating［J］.Computer Aided Engineering，2006，15（S）：15－18.（in Chinese）

［9］ 王宏宏，陈怀海，崔旭利，等.热效应对导弹翼面固有振动特性的影响［J］.振动、测试与诊断，2010，30（3）：275－279.

Wang Honghong，Chen Huaihai，Cui Xuli，et al，Thermal effect on dynamic characteristics of a missle wing［J］.Journal of Vibration，Measurement ＆ Vibration，2010，30（3）：275－279.（in Chinese）

［10］吴志刚，惠俊鹏，杨超.高超声速下翼面的热颤振工程分析［J］.北京航空航天大学学报，2005，31（3）：270－273.

Wu Zhigang，Hui Junpeng，Yang Chao.Hypersonic aerothermoelastic analysis of wings［J］.Journal of Beijing University of Aeronautics and Astronautics，2005，31（3）：270－273.（in Chinese）

［11］张伟伟.超声速、高超声速非线性气动弹性问题研究［D］.西安：西北工业大学，2004.

［12］陈桂彬，邹从青，杨超.气动弹性设计基础［M］.北京：北京航空航天大学出版社，2004：107－109.

［13］叶正寅，张伟伟，史爱明，等.流固耦合力学基础及其应用［M］.哈尔滨：哈尔滨工业大学出版社，2010：107－108.

［14］赵永辉.气动弹性力学与控制［M］.北京：科学出版社，2007：280－282.

［15］Rodden W P，Johnson E H.MSC／NASTRAN version 68，aeroelastic analysis user′s guide［R］.Santa Ana：MSC.Software Corporation，2002.

［16］叶献辉，杨翊仁.气动加热下三角机翼颤振［J］.西南交通大学学报，2008：43（1）：62－66.

Ye Xianhui，Yang Yiren.Flutter of delta wing under aerodynamic heating［J］.Journal of Southwest Jiaotong University，2008，43（1）：62－66.（in Chinese）