风轮固有振动频率随工况变化的响应特性＊

马剑龙， 汪建文， 魏海娇， 董 波

（1.内蒙古工业大学能源与动力工程学院 呼和浩特，010051）

（2.风能太阳能利用技术省部共建教育部重点实验室 呼和浩特，010051）

引 言

风力发电机是通过风轮叶片汲取风能，进而将机械能转化为电能的装置。风轮是风力发电机能量转化的关键动力部件，其动频参数决定着风力机的安全稳定运行及寿命。如何准确获得风轮的主要动频（即风轮动态振动频率）参数及其随工况变化的响应特性，是风能行业一直关注的热点问题。

风轮动频的获得有计算模态和试验模态两种方法。前者属典型的流固耦合问题，是较新的交叉学科问题。由于流固耦合求解理论和方法发展的滞后，使得该方面的研究仍处于起步阶段，因而利用计算模态方法准确获得风轮动频存在较大难度。试验模态法获得风轮动频的结果相对准确，但由于风轮旋转所产生的离心力和振动效应，特别是小型水平轴风力机多为高速旋转机械，使得在叶片表面布置加速度传感器进行测试在现阶段仍很难实现，所见相关报道多将加速度传感器布置于发电机头部靠近风轮处获得相应振动频谱，进而利用谱分析法对风轮动频进行研究［1］。

国外针对风轮动频的主要研究方向为模态计算新理论和试验新技术、新方法的开发，以及不同工况下风轮动频完整和准确获取的方法。Richard等［2］开发了热点激活法用于风力机的测试。Griffith等［3］提出了不同边界条件下几种新的模态测试方法。Kusnickt等［4-5］分别将模态滤波技术应用于风力机的模态测试。Krystal等［6］将SHM技术与风轮模态测试技术相结合，对风轮进行结构动力学性能测试。Schmidt等［7］使用跟踪摄影测量系统对风力机进行动态现场测量。Ganeriwala等［8］将叶片具有不同诱导裂纹与模态测试技术进行了有效结合。

国内关于风轮模态分析方面的研究工作仍以数值计算为主［9］。由于风电叶片截面具有不规则特征，采用传统的Bernoulli－Euler Beam模型求解其低阶固有频率非常困难［10］，各类新计算解法正处于开发阶段，且可靠性有待相关试验数据的验证；因此，现阶段利用先进测试设备针对风轮动频开展研究是有效的实现手段，并可为相关模拟计算提供相对可靠的参考试验数据。但是，我国在风力机振动测试方面的研究仍处于起步阶段［11-12］，研究同时发现，单纯以来流风速增大或风轮转速增大定义气动载荷升高，从而得出风轮动频升高和降低两种截然相反的结论。

笔者利用数值计算与试验研究相结合的方法，针对某小型水平轴风力机风轮在不同工况下进行动频研究，分析了离心力和气动载荷对风轮动频的影响，考证了风轮1，2阶振动频率随工况变化的敏感性，揭示了风轮动频随工况变化的响应特性。同时，提出了通过风轮转矩变化的方法分析风轮受力，进而识别风轮动频变化规律的方法，解决了单纯以来流风速变化或风轮转速变化判别风轮动频变化而造成的误判。

1 数值计算

1.1 研究对象

研究对象为某小型水平轴风力机三叶片风轮，风轮直径为1.4m，叶片材质为木质。为单纯考察风轮的动频特性，研究中建模不涉及发电机和塔架，且为避免风轮部件的结构简化可能对计算结果造成的影响，模型依实体建立，如图1所示。

图1 风轮模型Fig.1 Model of the wind wheel

1.2 气动力方程及求解

气动力是气流流过各叶素面的微元力总和

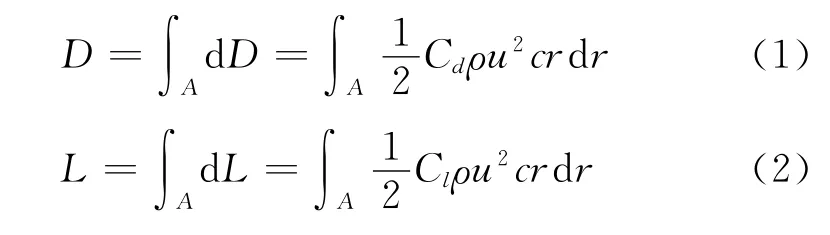
其中：D，L为叶片表面阻力和升力；Cd，Cl为阻力系数和升力系数；ρ，u为空气密度和来流风速；c为叶片平均弦长；r为半径为r处的叶素微元。

采用稳态计算，进口边界采用速度入口，出口边界采用压力出口，相对压力为0。风轮旋转区域采用滑移网格，静止壁面满足无滑移条件。数值计算中应用能量方程、动量方程、连续方程和SST方程进行耦合求解。

1.3 叶片结构动力学方程及求解

根据风轮几何参数，运用有限元方法构建离散化方程，运动方程为

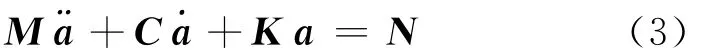
其中：M，C，K分别为系统的质量矩阵、阻尼矩阵和刚度矩阵；N为在变载荷作用下的外界激励，如离心力、气动力等；¨a，˙a，a分别为叶片有限元结点的加速度、速度、位移矢量。

N＝0时，由于外界系统对测量系统激励为0，方程有非零解，叶片处于自由振动状态，此时方程反映了风轮本身的固有特性——风轮固有频率及振型。若不计阻尼作用，求解方程特征为

进而得到结构振型矩阵Φ＝（Φ1，Φ2，…，Φi），固有角频率

N＝F时，外界激励为气动力。N＝Q时，外界激励为离心力，离心力矩阵方程为

其中：Q为离心力矩阵；Ω为叶片旋转角速度。

给定约束条件后，在不同工况下，导入前期计算获得的气动场数据，并添加离心力参数，进行结构动力学方程求解，进而得到风轮的动态响应，如振型，频率等。

1.4 计算结果及分析

1.4.1 算例1

定义v为风速，λ为尖速比，f1f为1阶反对称振动频率，f1d为1阶对称振动频率，f2f为2阶反对称振动频率，f2d为2阶对称振动频率。

以风轮叶尖转速为40m／s，来流风速分别为5～10m／s为例，风轮1，2阶振动频率计算结果如表1所示。

为分析风轮1，2阶动频随工况变化的敏感性，对于同一类型振动，定义表1中各振动频率的增幅d1如下

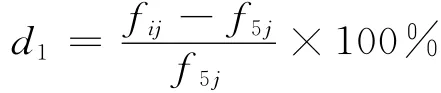
其中：d1为增幅；fij为风速为i时j类振动频率（i＝5，6，7，8，9，10m／s；j＝f1f，f1d，f2f，f2d）；f5j为风速度为5m／s时j类振动频率。

在不考虑离心力的工况下，气动载荷变化对风轮1，2阶动频影响的敏感性如图2所示。

从图2中数据变化趋势可以发现，风轮保持相同的转速时，来流风速增大，风轮的动频升高。这是因为风轮转速相同时，来流风速变大，风轮的转矩增大，进而造成叶片周向内应力增大，风轮动频升高。

同时，从图2中各曲线斜率可得出结论：风轮1阶振动频率随气动载荷变化的敏感性显著强于2阶动频，同阶对称振动频率随气动载荷的变化较反对称振动明显；1阶振动频率随气动载荷变化的生长规律呈二次方曲线形式，2阶振动频率随气动载荷变化的生长规律成线性。

表1 相同转速、不同来流风速时风轮振动频率随工况的变化Tab.1 Vibration frequency of the wind wheel changing with the working condition under the same rotational speed and the different wind velocity

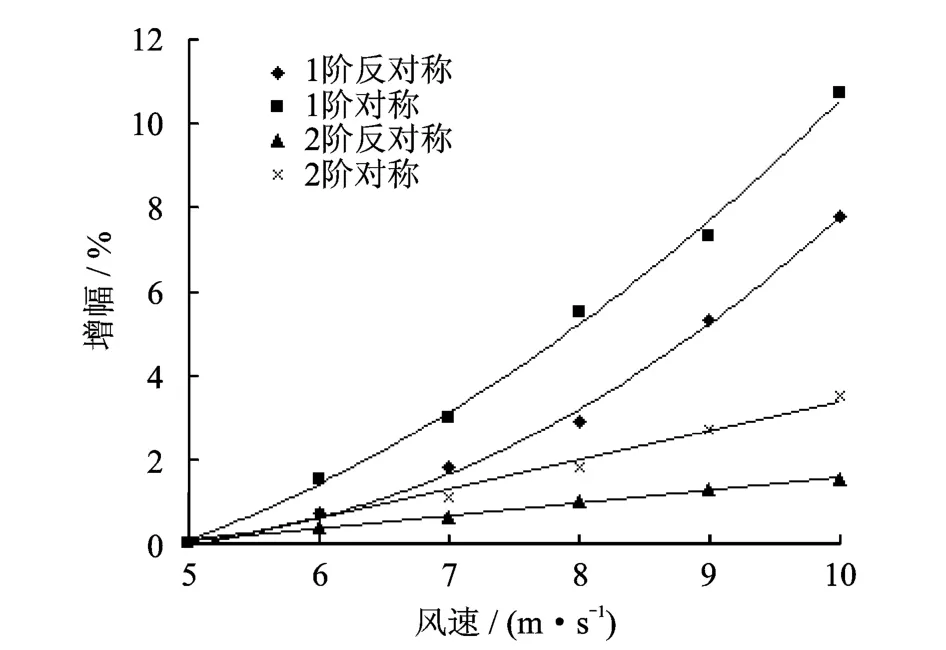
图2 无离心力时风轮1，2阶动频随气动载荷的变化Fig.2 The 1－order and 2－order vibration frequency of the wind wheel changing with the aerodynamic load under ignoring the centrifugal force

由于该算例中风轮保持相同的转速，故在不同工况下风轮具有相同的离心力。因此，对比表1中各工况下有、无离心力时的计算数据可以发现，在考虑离心力状态下，由于离心力的存在，使叶片旋转过程中内部产生径向拉应力，进而造成风轮动频增大。由于风轮转速相同，离心力对风轮各工况下1，2阶动频的影响程度基本相同。

1.4.2 算例2

以来流风速为8m／s，尖速比分别为5～8为例，风轮1，2阶振动频率计算结果如表2所示。为分析风轮1，2阶动频随工况变化的敏感性，对于同一类型振动，定义表2中各振动频率的增幅d2如下

其中：d2为增幅；fij为尖速比为i时j类振动频率（i＝5，6，7，8；j＝f1f，f1d，f2f，f2d）；f5j为尖速比为5时j类振动频率。

在不考虑离心力的工况下，单纯考虑气动载荷变化对风轮1，2阶动频影响的敏感性如图3所示。

图3 无离心力时风轮1，2阶动频随气动载荷的变化Fig.3 The 1－order and 2－order vibration frequency of the wind wheel changing with the aerodynamic load under ignoring the centrifugal force

从图3中数据变化趋势可以发现，来流风速相同时，随尖速比增大，风轮的动频下降，这与前者风轮保持相同转速，来流速度增大情况下所获结论恰好相反。从表面上看，两者结论是相悖的，但实质却不然。分析原因为，来流风速相同，随风轮尖速比增大，风轮的转矩实质上变小，进而造成叶片周向内应力减小，风轮动频随之下降。

表2 相同来流风速、不同尖速比时风轮振动频率随工况的变化Tab.2 Vibration frequency of the wind wheel changing with the working condition under the same wind velocity and the different tip－speed ratio

图3中各曲线斜率的变化规律再次证实：风轮1阶振动频率随气动载荷变化的敏感性显著强于2阶动频，同阶对称振动频率随气动载荷的变化较反对称振动明显；1阶振动频率随气动载荷变化的生长规律呈二次方曲线形式，2阶振动频率随气动载荷变化的生长规律成线性。

同时考虑气动载荷和离心力时，风轮1，2阶振动频率随工况的变化如图4所示。

图4 同时考虑气动载荷和离心力时风轮1，2阶动频随工况的变化Fig.4 The 1－order and 2－order vibration frequency of wind wheel changing with the working condition under considering the the centrifugal force and the centrifugal force

对比图3，4中数据的差异性可以发现，在离心力加入后，图3中数据变化趋势变成了截然相反的走势，即随尖速比增大，风轮1，2阶动频增大。由此得到结论：离心力对风轮动频的影响显著强于气动载荷。这是由于研究对象为小型风力机风轮，叶片为木质实心结构，且叶片直径较小，因而叶片刚度较大，气动载荷引起的叶片变形量较小，从而附加产生的叶片内应力较小，故对叶片动频影响较小。正是由于叶片为实心结构，风轮叶片具有较大的质量，旋转过程中叶片内部产生了很强的径向拉应力，从而对叶片动频存在更为显著的影响。

2 静频试验

2.1 测试系统、测试原理及测试方法

测试系统采用丹麦B＆K公司最新研发的PULSE16.1结构振动分析系统，测试原理如图5所示。

图5 模态测试原理Fig.5 Test principle of the static frequency

试验设备及传感器布置如图6所示。测试试验在内蒙古工业大学新能源基地的B1／K2低速风洞开口试验段前、小型风力机专用测试台架上完成。风轮依实际运行工况安装，风轮和发电机主轴间为螺栓直接连接，发电机安装于测试塔架之上。

图6 测试设备及传感器布置Fig.6 Test equipment and the arrangement of sensors

测试方法采用瞬态激振法，单点激励，多点响应。力锤采用橡胶头力锤，振动频率采集范围设置为0～400Hz，激励点选为图7中的43号点，激励方向垂直于激励点处叶面。理论上分析，选择叶片上的任意点产生激励，均不会影响到测试效果。但实际测试中，每次力锤激励测试，系统默认一定的测试时长（即反应时间），而该时长内，力锤不可以再次发生激励，否则会造成测试失败。如图7所示，43号点靠近叶根处，由力锤激励后所产生的振动位移小，有利于力锤激励后顺利地摆脱叶片，以有效防止叶片由于振动向上回弹与力锤发生附加碰撞，造成连击，进而造成测试失败。由此分析，40～45号点均较适于作激励点，但由于激励方向应垂直于激励点所在位置面，考虑到叶片扭角的存在和敲击方便、准确，选择43号点最为适宜。

2.2 数据处理

试验数据采用ME／scopeVESv5.1软件进行处理。软件中模型的建立及测点的对应分布如图7所示。试验数据的拟合及对应振动参数的获得如图8所示。

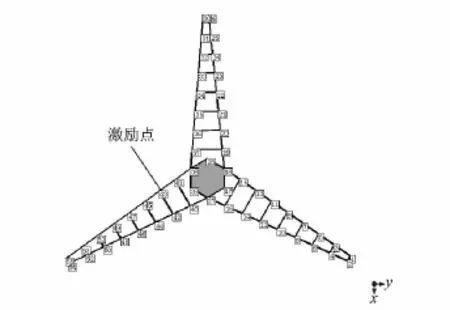
图7 风轮模型Fig.7 Model of the wind wheel

图8 风轮振型及固有频率Fig.8 Mode shapes and natural frequency of the wind wheel

图8中，左侧区域为选取的频率所对应的振型图（示例为1阶对称振动，对应固有频率为24.9 Hz），图中平直的线面为风轮未被力锤激励时所处的位置面，弯曲的线面为风轮振动时叶片变形后所处的线面；中间区域为测试数据的拟合和收敛，下侧曲线的峰点对应获得的各振动（峰点并不全是典型振动方式，可能为被测叶片自身特有振动方式，因而需根据左侧振型图予以判断），峰点横坐标为该振动所对应的频率，纵坐标为该振动所对应的振动加速度；右侧区域为各曲线峰点所对应的频率值，示例中YES（绿色）项为判定后所选择的风轮典型振动，从上向下依次对应的振动特性为轴向窜动效应、圆盘效应、1阶反对称、1阶对称、2阶反对称、2阶对称、3阶反对称、3阶对称。

2.3 测试结果

风轮1，2阶振动频率如表3所示。

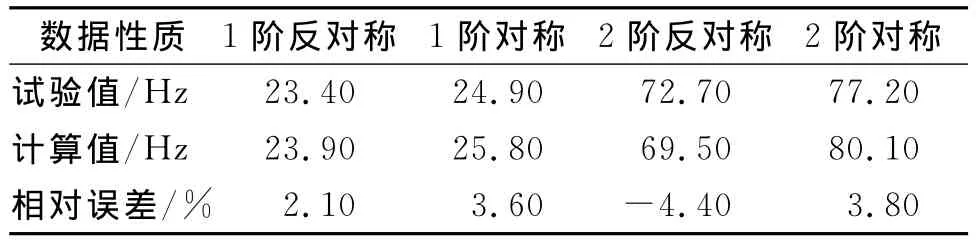
表3 风轮振动特性及对应频率Tab.3 Vibration characteristics and corresponding frequencies of the wind wheel

3 动频试验

3.1 测试对象、测试系统及测试方法

测试对象是依数值计算模型加工制作的实体叶片。测试系统采用B＆K公司研发的PULSE16.1结构振动分析系统，测试原理如图9所示。

图9 动频测试原理Fig.9 Test principle of the dynamic frequency

测试方法采用布置于发电机前端部靠近风轮处的加速度传感器捕获振动频谱，通过静态频谱结合谱分析法识别风轮动频。试验设备如图10，11所示。

图10 试验设备Fig.10 Test equipment

图11 传感器布置Fig.11 Arrangement of sensors

振动信号分别由4个加速度传感器感知，布置位置的编号如下：1为发电机顶部前端；2为发电机侧部前端；3为发电机顶端中部；4为发电机下端（见图11）。

测点处振动信号由加速度传感器感知，并通过数据线传输给数据采集卡，振动信号采集时各参数的设置由PULSE系统软件完成，如图10（b）中的右侧电脑；风轮输出功率信号由EDA9033G智能三相电采集设备完成，风轮转速由功率间接获得，如图10（b）中的左侧电脑；同一来流风速下，风轮不同转速的调节通过滑动变阻器改变系统负载实现。

3.2 试验方案可靠性分析

小型风力机风轮属高速旋转机械，通过在叶片表面直接布置加速度传感器进行风轮动频测试，在现阶段仍很难实现。常用方法是在发电机前端靠近风轮处布置加速度传感器获得风轮振动频谱，进而通过谱分析法分析风轮动频。本试验方法的可靠性可通过以下4个方面予以判断：a.动态频谱与静态频谱是否具有相似性；b.1，2号传感器捕获频谱是否存在一致性；c.3，4号传感器与1号传感器捕获频谱是否存在差异性；d.实际测试中，动频频谱共振点所对应转速附近，风轮振动强度是否明显增强。

以风轮在来流风速为10m／s、尖速比为6时（该工况为风轮设计额定工况）为例，通过1～4号传感器捕获的动频如图12所示。

图12 风轮动态频谱图Fig.12 Dynamic spectrogram of the wind wheel

对比静态频谱图8和动态频谱图12中各分图发现：1，2号传感器振动频谱保持很好的一致性；1号传感器振动频谱与静态频谱有很好的相似性，只是各振动加速度值和频率值有所差异，这是由于风轮的离心力和气动载荷使静、动频存在差异性所致；3，4号传感器振动频谱与静态频谱的吻合性下降很多。分析原因为：1，2号传感器布置于发电机前端部，紧靠风轮处，受风轮振动特性影响明显，故振动频谱图与静态频谱相似性效果好；3号风轮位于发电机上端中部，该处距离风轮较远，距离电机工作的励磁线圈较近，频谱受励磁线圈振动特性影响较大，故部分振动峰值较模糊，难以识别风轮的实际振动特性；4号传感器远离风轮，靠近塔架，其捕获的频谱特性明显有别于其他动态频谱和风轮静态频谱。故综合分析，以1号传感器捕获的振动频谱为基础，通过静频结合谱分析法获得风轮的动频相对可靠。同时，1，2号传感器虽布置位置不同，但两者获得的频谱高度一致，从另一方面证实了测试方法的可靠性。动频测试中，在动频频谱共振点所对应转速附近，观测到风轮的振动强度明显增强，从而最直接地证明了测试方法对动频获得的可靠性。

由风轮频谱图12（a），结合牛顿力学经典公式F＝ma可知，风轮旋转过程中质量不发生变化，故各振动所触发的振动应力与振动加速度值成正比。由此获得结论，风轮1阶振动应力大于2阶振动应力；同阶对称振动应力大于反对称振动应力。

3.3 测试结果

由于笔者仅针对风轮振动频率随工况变化的响应特性进行分析，以下分析中将不涉及风轮的轴向窜动效应和圆盘效应两种振动方式，该两类振动请参阅文献［11］。

为验证前者两个算例中数值计算结果的可靠性，使风轮叶尖旋转速度保持在40m／s，不同来流风速下风轮动频试验值与计算值对比如表4所示。另一方面，使来流风速保持在8m／s，尖速比分别为5～8时，风轮1，2阶动频试验值与计算结果对比如表5所示。

定义表4，5中相对误差δ如下

其中：δ为相对误差；fj，fs分别为同一工况下同一类振动频率的计算值和试验值。

通过表4、表5中数据的误差分析可知，计算值与试验值存在很好的一致性，总体误差保持在10%以内，验证了数值计算结果的可靠性，同时也验证了风轮1，2阶振动频率随工况变化响应特性方面所获结论的可靠性。

计算值与试验值必然存在差异，这是因为试验是通过布置于发电机前端部靠近风轮处的加速度传感器捕获频谱，这与数值计算理想的只针对风轮模型进行分析存在客观的差异性。

表4 相同转速、不同来流风速下风轮1，2阶动频试验值与计算值对比Tab.4 Compared between the experimental data and the calculated data under the same rotational speed and the different wind velocity

表5 相同来流风速、不同尖速比下风轮1，2阶动频试验值与计算值对比Tab.5 Compared between the experimental data and the calculated data under the same wind velocity and the different tip－speed ratio

4 结束语

利用数值计算与试验研究相结合的方法，针对直径为1.4m的小型水平轴风力机风轮1，2阶振动频率随气动载荷和离心力变化的响应特性进行了分析。研究结果表明：离心力对风轮动频的影响明显较气动载荷显著；风轮1阶动频随气动载荷变化的敏感性显著强于2阶动频，同阶对称振动频率随气动载荷变化的敏感性明显强于反对称振动频率；1阶动频随气动载荷变化的生长规律呈二次方曲线形式，2阶动频随气动载荷变化的生长规律成线性。研究同时发现，风轮1阶对称振动频率随气动载荷和离心力的变化最为敏感，该种振动所触发的振动应力明显强于风轮其他1，2阶振动应力，故其应作为风轮结构动力学特性设计中最值得关注的参数。

笔者采用风轮气动转矩随气动载荷变化（气动载荷变化涉及来流风速和风轮转速两个因素）的关联关系，利用气动转矩与风轮周向内应力的关联规律，很好地解释了气动载荷变化对风轮动频的影响，有效解决了单纯以来流风速增大或风轮转速增大定义气动载荷升高，从而得出风轮动频升高和降低两种截然相悖结论的问题。

［1］ 汪建文，闫建校，刘博，等.谱分析法测量叶尖小翼对风轮旋转时固有频率的影响［J］.工程热物理学报，2007，28（5）：784－786.

Wang Jianwen，Yang Jianxiao，Liu Bo，et al.The determination of the influence of tip vane for natural frequency of the rotating wind turbine using spectrum analysis［J］.Journal of Engineering Thermophysics，2007，28（5）：784－786.（in Chinese）

［2］ Richard O，Gunjit B，Heena M.Full－scale modal wind turbine tests：comparing shaker excitation with wind excitation［C］∥Proceeding of the 28th IMAC，Structural Dynamics and Renewable Energy.New York：Springer，2011：113－124.

［3］ Griffith D T.Experimental modal analysis of 9－meter research－sized wind turbine blades［C］∥Proceeding of the 28th IMAC，Structural Dynamics and Renewable Energy.New York：Springer，2011：1－14.

［4］ Kusnick J F.Vertical axis wind turbine operational modal analysis in sheared wind flow［C］∥Proceeding of the 30th IMAC：Topics in Experimental Dynamics Substructuring and Wind Turbine Dynamics.New York：Springer，2012：333－344.

［5］ Garcia M，Reich A.Real－time dynamic measurements of a wind turbine rotor blade using modal filtering［C］∥IMAC－ⅩⅩⅤⅡ：Conference and Exposition on Structural Dynamics－Model Verification and Validation. New York：Springer，2009：214－216.

［6］ Krystal D，Timothy M.Modal analysis and SHM investigation of CX－100wind turbine blade［C］∥Proceeding of the 29th IMAC：Rotating Machinery，Structural Health Monitoring，Shock and Vibration.New York：Springer，2011：413－438.

［7］ Schmidt P U，Tim S，Oliver E.Developments in large wind turbine modal analysis using point tracking video grammetry［C］∥Proceeding of the 28th IMAC，Structural Dynamics and Renewable Energy.New York：Springer，2011：187－198.

［8］ Ganeriwala S N，Yang Jun，Richardson M.Using modal analysis for detecting cracks in wind turbine blades［J］.Sound and Vibration，2011，45（5）：10－13.

［9］ 康顺，尹景勋，刘云飞.水平轴风力机结构动力学分析［J］.工程热物理学报，2009，30（5）：777－780.

Kang Shun，Yin Jingxun，Liu Yunfei.Structure dynamic analysis of horizontal axis wind turbines［J］.Journal of Engineering Thermophysics，2009，30（5）：777－780.（in Chinese）

［10］王磊，陈柳，何玉林，等.基于假设模态法的风力机动力学分析［J］.振动与冲击，2012，31（11）：122－126.

Wang Lei，Chen Liu，He Yulin，et al.Dynamic analysis of a wind turbine base on assumed mode method［J］.Journal of Vibration and Shock，2012，31（11）：122－126.（in Chinese）

［11］马剑龙，汪建文，董波，等.风力机风轮低频振动特性的实验模态研究［J］.振动与冲击，2013，32（16）：164－170.

Ma Jianlong，Wang Jianwen，Dong Bo，et al.Experimental modal analysis on low－frequency vibration characteristics of wind turbine［J］.Journal of Vibration and Shock，2013，32（16）：164－170.（in Chinese）

［12］徐玉秀，王志强，梅元颖.叶片振动响应的长度分形故障特征提取与诊断［J］.振动、测试与诊断，2011，31（2）：190－192.

Xu Yuxiu，Wang Zhiqiang，Mei Yuanying.Fault feature extraction and diagnosis for wind turbine blades from vibration response based on theory of length fractal dimension［J］.Journal of Vibration，Measurement＆ Diagnosis，2011，3（2）：190－192.（in Chinese）