风险导向审计中风险环节权重的重构与修正研究——基于条件概率和贝叶斯定理

○董丽虹

（人民银行银川中心支行内审处 宁夏 银川 750001）

一、引言

国际内部审计实务标准及其最新发展趋势表明，内部审计应采用风险导向审计理论和方法，更好地履行内部审计职能。风险导向审计是内部审计人员通过对被审计对象风险的分析与评价，全面把握被审计对象的风险状况，根据量化风险水平识别高风险领域，在此基础上确定审计重点和频率，以便合理配置审计资源和协助管理风险，实现审计价值增值的独立、客观的签证和咨询活动。近年来，我国学术界就风险导向审计做了大量的研究，深入阐述了风险导向审计的涵义、特征，并结合当前我国内部审计的现状，提出了推进风险导向内部审计模式应用的策略。

人民银行开展风险导向审计是与国际先进审计标准接轨的必然趋势，也是符合央行职能转变和业务发展需要的必然要求。《人民银行内审工作转型2011—2013年规划》的制定积极推进了内审工作的转型与发展，各基层行运用“风险引导审计，审计关注风险”的内部审计理念，从实施风险导向审计的基础与环境，风险导向审计模式的构建以及风险导向审计模式的应用路径等方面进行了深入的探索。然而，风险导向审计的关键环节是风险评估，在风险评估过程中，风险因素权重的设定对评估结果的准确性起着至关重要的作用，如何验证权重设定的科学性和准确性，并根据审计实践对风险权重进行重构与修正成为我们亟待解决的难题。

二、条件概率和贝叶斯定理

根据《概率论》，采用标准差作为风险测量指标，彻底避开了先实施风险登记量化赋值，再根据量化值测量风险这种主观性较强的评估模式，并在实务操作中，结合被审计主体的履职目标进行风险识别，梳理其各风险因素（即风险类型、风险环节和风险点）。将概率概念纳入风险分析框架，不仅有力地克服了事先给定权重的人为因素，使得审计结果更加真实可靠，也为我们的研究提供了一种启示和思路，也就是从概率的角度，对权重进行重构并结合审计实践进行修正，以期达到更加理想的结果。本文从简要介绍概率论和贝叶斯定理的原理和计算方法到基层央行的审计实践，阐述了联合概率在风险环节权重重构方面的应用，以及结合具体审计实际工作运用贝叶斯定理对这一权重进行修正的具体方法。

贝叶斯定理机率论或概率论是研究随机性或不确定性等现象的数学。人们根据不确定性信息作出推理和决策需要对各种结论的概率作出估计，这类推理称为概率推理。概率推理既是概率学和逻辑学的研究对象，也是心理学的研究对象，但研究的角度是不同的。概率学和逻辑学研究的是客观概率推算的公式或规则，而心理学研究人们主观概率估计的认知加工过程规律。贝叶斯推理的问题是条件概率推理问题，这一领域的探讨对揭示人们对概率信息的认知加工过程与规律，指导人们进行有效的学习和判断决策都具有十分重要的理论意义和实践意义。

1、概率的几种表示方式

条件概率：就是事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为P（A|B），读作“在B条件下A的概率”。条件概率公式：

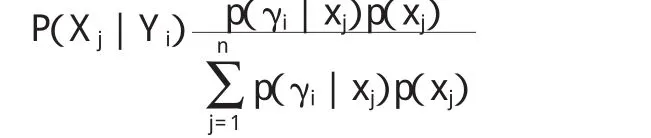
联合概率：表示两个事件共同发生的概率。A与B的联合概率表示为 P（A B）或者 P（A，B）。

边缘概率：是某个事件发生的概率，而与其它事件无关。边缘概率是这样得到的：在联合概率中，把最终结果中不需要的那些事件合并成其事件的全概率而消失（对离散随机变量用求和得全概率，对连续随机变量用积分得全概率）。这称为边缘化（marginalization）。A的边缘概率表示为P（A），B的边缘概率表示为 P（B）。

需要注意的是，在这些定义中A与B之间不一定有因果或者时间顺序关系。A可能会先于B发生，也可能相反，也可能二者同时发生。A可能会导致B的发生，也可能相反，也可能二者之间根本就没有因果关系。

考虑一些可能是新的信息的概率条件性可以通过贝叶斯定理实现。

2、贝叶斯定理

贝叶斯定理由英国数学家贝叶斯（Thomas Bayes 1702-1761）发展，用来描述两个条件概率之间的关系，比如P（A|B）和P（B|A）。根据《概率论》中条件概率的讨论中，我们可知，在获得新的信息之后对概率进行修正，是一种很重要的概率分析手段。经常地，我们开始分析时，总以初始的或先验的概率对所关心的特殊事件进行估计，然后，我们从一些诸如样本、报告和统计实践等信息源中获得了有关该事件的新的信息，有了这些信息，我们就能通过计算对先验概率值进行修正，从而变为后验概率。贝叶斯定理就是进行这种概率计算的一种方法。

早在18世纪，英国学者贝叶斯（1702—1761）曾提出计算条件概率的公式用来解决如下一类问题：假设H[，1]，H[，2]…互斥且构成一个完全事件，已知它们的概率 P（H[，i]，i=1，2，…，现观察到某事件 A与H[，1]，H[，2]…相伴随而出现，且已知条件概率 P（A/H[，i]），求 P（H[，i]/A）。

贝叶斯公式（发表于 1763年）为：P（H[，i]/A）=P（H[，i]）P（A│H[，i]）/[P（H[，1]）P（A│H[，1]）＋P（H[，2]）P（A│H[，2]）＋…]

这就是著名的“贝叶斯定理”，一些文献中把 P（H[，1]）、P（H[，2]）称为基础概率，P（A│H[，1]）为击中率，P（A│H[，2]）为误报率[1]。

三、条件概率和贝叶斯定理在风险环节权重重构与修正中的应用

1、风险环节权重的重构

我们借鉴基层行的研究，根据被审计主题的履职目标进行风险识别，梳理出各风险因素（即风险类型、风险环节和风险点）。以往的审计实践中，对于风险环节权重的赋值，存在较为严重的人为因素，使得最后的得分具有或轻或重的不可信和不可靠。所以，有必要克服风险环节权重确定的这一人为因素。

我们知道风险环节风险权重的高低不仅受到风险点风险程度的影响，而且与其多少存在正相关，因此，可以根据风险点的多少构造风险环节与风险点风险情况来重构风险环节风险权重的多少。以基层行对货币发行管理的审计实践为例：如表1所示。

其中，风险点风险程度高、中、低个数的设定是根据审计内容确定的。A1，A2，A3，A4，A5，A6，A7，A8，A9，A10，A11，A12分别表示“制度建设及人员配置”，“库区设施”，“组合锁使用管理”，“基本制度执行情况”，“人员进出库区管理”，“库存实物管理”，“出入库业务管理”，“货金系统管理”，“会计核算”，“残损币销毁”，“应急管理”，“职业道德”。

表1 风险环节与风险点情况表

表2 风险环节与风险点联合概率分布表

现在我们根据《概率论》中条件概率的知识，构造表2：风险环节风险权重的联合概率分布表。在联合概率分布表的边缘分别列出了每个风险环节的概率。即P（A1）=0.066176…….。这些概率就是边际概率。根据边际概率，我们知道7%为“制度建设及人员配置”的权重，6%为“库区设施”的权重，7%为“组合锁使用管理”的权重，13%为“基本制度执行情况”的权重，4%为“人员进出库区管理”的权重，8%为“库存实物管理”的权重，11%为“出入库业务管理”的权重，10%为“货金系统管理”的权重，4%为“会计核算”的权重，11%为“残损币销毁”的权重，13%为“应急管理”的权重，6%为“职业道德”的权重。

接下来的具体审计实际中，我们以此边际概率作为各个风险环节权重的赋值进行分值的计算，这样就可以避免风险环节权重量化赋值的人为估值因素，有利于增强审计结果的真实性和可靠性。

2、风险环节权重的修正

经常地，我们开始的分析总以初始的或先验的概率对所关心的特殊事件进行估计，然后，我们从一些诸如样本、报告和统计实践等信息源中获得了有关该事件的新的信息，有了这些信息，我们就能通过计算对先验概率值进行修正，从而变为后验概率。贝叶斯定理就是进行这种概率计算的一种方法。用它来进行修正概率，其步骤如图1所示。

图1 利用贝叶斯定理进行概率修正

又如：在我们对国库业务风险管理审计的研究中，我们根据我们审计的具体实际工作需要，结合多年审计实践定义A1=“风险来自制度建设”，A2=“风险来自业务管理”，A3=“风险来自业务操作”，A4=“风险来自核算系统管理”，A5=“风险来自应急管理”，A6=“风险来自道德行为规范”。根据多年的审计实践初步设定先验概率 P（A1）=0.1，P（A2）=0.3，P（A3）=0.3，P（A4）=0.1，P（A5）=0.1，P（A6）=0.1。

风险的高低由于来源的不同而不同，六个风险来源的风险高低的审计实际数据见表3中。

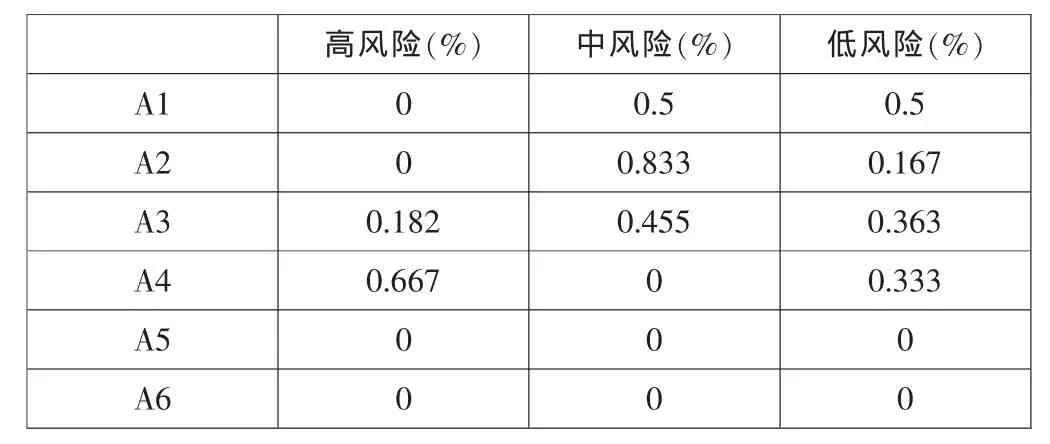
表3 风险环节的实际数据表

如果我们以G表示事件“高风险”，M表示事件“中风险”，N表示事件“低风险，则表1中的信息可以用下面的条件概率来表示：

P（G—A1）=0P（M—A1）=0.5 P（N—A1）=0.5

P（G—A2）=0P（M—A2）=0.833 P（N—A2）=0.167

P（G—A3）=0.182 P（M—A3）=0.455 P（N—A3）=0.363

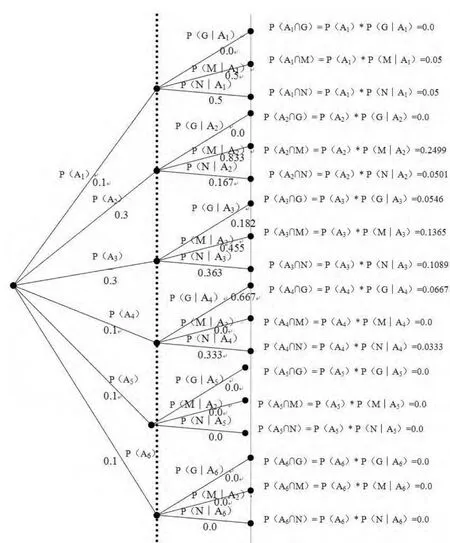
图2 风险环节的概率树

P（G—A4）=0.667 P（M—A4）=0P（N—A4）=0.333

P（G—A5）=0P（M—A5）=0P（N—A5）=0

P（G—A6）=0P（M—A6）=0P（N—A6）=0

我们可以用树形图表示这个两步骤实验。我们首先从六个风险环节的某一环节出发，然后再检验这个风险环节里风险点的风险高中低。我们看到最终有18个实验结果。

我们看到每个实验结果都是两个事件的交，可以利用乘法公式计算其概率，比如：

现在来自这六个风险环节的风险被用到审计实践中，在已知存在风险的信息后，根据著名的“木桶原理”可以从“低”风险这一层面对来自风险环节的概率进行修正，即“低”风险分别来自 A1，A2，A3，A4，A5，A6的概率为多少。有了概率树上的信息（图2），用贝叶斯定理就可以解答这样的问题。

N表示事件“低风险，我们现在要求后验概率P（A1—N），P（A2—N），P（A3—N），P（A4—N），P（A5—N），P（A6—N），从条件概率公式，我们知道

参考概率树，我们看到

为求 P（N），我们有

P（N）=P（A1∩N）+P（A2∩N）+P（A3∩N）+P（A4∩N）+P（A5∩N）+P（A6∩N）

=P（A1）*P（N—A1）+P（A2）*P（N—A2）

+P（A3）*P（N—A3）+P（A4）*P（N—A4）

+P（A5）*P（N—A5）+P（A6）*P（N—A6）

（3）

将式（2）和式（3）代入式（1）中，并以类似方法得到 P（A2—N），P（A3—N），P（A4—N），P（A5—N），P（A6—N）的结果。

在本例中，计算结果：

P（A1—N）=0.2064

P（A2—N）=0.2068

P（A3—N）=0.4494

P（A4—N）=0.1374

P（A5—N）=0.0000

P（A6—N）=0.0000

我们注意到，开始时对于风险有0.1的概率“来自制度建设”，但是，在实际审计中给定了存在风险的信息以后，则这个风险“来自制度建设”的概率上升到了0.2064。这样，根据修正后的风险概率和审计实际中的扣分值，按照比率计算方法，最终得到修正后的实际得分值。本例中在审计实际中，原来是按0.1的概率扣分0.3分，则按修正后的0.2064概率的扣分值为0.2064*0.3/0.1=0.6192分，进而得到实际得分值，这样就会得到整个风险环节的实际得分值，以此为例，被审计行按照修正后的实际分值为82分，原来按照多年审计实践初步人为设定的概率计算的实际分值为84.3分，二者比较分值相近，这充分说明贝叶斯后验修正概率定理可以运用到具体的审计实践中，并且可以取得预期的效果。

四、结论

人民银行开展风险导向内部审计是一门新的课题，尽管近几年来人民银行在内部审计实践中就如何应用风险导向审计模式也摸索出了一定的方法，但是目前风险导向审计仍然处于积极探索阶段。本文从概率论中联合概率分布和贝叶斯后验定理的视角，探索构建了风险环节权重，并依据审计实际工作对其系数进行了修正，取得了预期的结果。同时，风险导向内部审计也是一项系统工作，本文只是在克服根据先验事先给定权重的人为因素和定量评估风险环节的权重方面做了一些探索，就风险点风险程度高、中、低的设定也存在着一定的人为因素。因此，有关这方面的研究有待进一步深入。

[1]刘文俊：风险导向内部审计模式的应用[J].商业会计，2010（22）.

[2]刘曼惠：风险导向内部审计策略探析[J].现代商业，2010（32）.

[3]付春：完善风险导向审计的应用[J].会计之友，2009（10）.

[4]李晓春、高维红：实行风险导向内部审计的难点和对策[J].商业会计，2010（20）.

[5]张越：风险导向审计在内部审计应用中的探索[J].现代审计与经济，2009（4）.

[6]王孝玲：现代风险导向审计在人民银行内部审计中的应用探析[J].西部金融，2010（2）.

[7]中国人民银行武汉分行内审处课题组：风险导向审计模式在人民银行风险管理中的应用[J].中国内部审计，2010（1）.