桥梁施工临时结构体系可靠性评估方法

聂瑞锋，石雪飞，阮 欣

（同济大学 土木工程学院，上海200092）

因临时结构具有可加工性强、重复利用率高等优点而被广泛应用于各类桥梁的施工中.大量因临时结构失效引发的施工事故［1-2］引起国内外学者的高度关注，并对其合理的设计方法做了相关理论和试验研究，但研究均未考虑临时结构自身和荷载变异性的影响［3-5］.业内多采用安全系数法进行设计，其采用人为增大荷载效应的方法考虑施工过程中的不确定性，但该方法往往导致过分保守的设计，造成不必要的浪费［3］.目前，可靠度的方法已广泛应用于结构的性能评估中，但采用可靠度的方法对施工中临时结构进行分析的研究较少.文献［6］对人行通道脚手架节点连接在强风下的可靠性进行研究.文献［7-8］对施工中建筑结构的失效概率进行研究，但研究未考虑临时结构失效的影响.文献［9］对不同连接方法的脚手架失效概率进行分析.但上述研究均体现在构件可靠度的层面，难以体现构件间的相互作用.而体系可靠度方法不仅能够较好地体现施工中临时结构抗力和荷载的变异性，还能保证设计结构具有一致的可靠度，且较传统基于构件可靠度的设计方法经济、可靠度高［10］.

本文首先基于体系可靠度的层面，采用有限元计算同串并联模型相结合的方法对临时结构的失效模式进行判定；其次，通过对现有文献资料的调研提出适用于临时结构抗力、荷载以及人因差错等随机变量的统计参数；最终，以一三角挂篮为对象，采用体系可靠度计算方法对其合理的受力状态及可靠度一致水平进行分析，以验证本文方法的适用性及合理性.

1 临时结构体系可靠度分析

1.1 体系失效模式

假定临时结构的抗力和荷载均服从正态分布且相互独立，则其失效概率Pf可按下式计算：

式中：Pf为结构的失效概率；为结构抗力R的均值；为永久荷载D的均值；为可变荷载L的均值；Φ（·）为标准正态分布函数；σR，σD和σL分别为R，D和L的标准差；β为可靠度指标.

结构的失效模式同结构构造、材料性质、受力形式等多种因素有关.对所有的失效模式都进行组合分析是不现实的，且各失效模式对结构体系可靠度的影响存在差异.目前，采用串并联的方法判断体系失效模式的方法已得到较好的应用［11-12］.临时结构构造相对简单，耦合度较低，其可能发生的失效行为是可预判的.而相关研究表明：结合试验或数值仿真等的串并联失效模型可靠度分析法，能够较好地适用于已知体系失效行为的结构［13］.因此，本文基于对临时结构构件的受力状态以及构件间相互作用的研究，采用串并联模型确定临时结构的失效模式.

1.2 目标可靠度指标选取

在构件层次，规范 CHBD［14］和 AASHTO［15］均采用3.75作为桥梁构件设计的目标可靠度指标，对于临时结构，建议其最优可靠度指标为3.5.我国《公路工程结构可靠度统一标准》［16］按结构破坏后造成的影响制定目标可靠度指标，共分为3个等级，其中对于延性破坏构件分别取用4.7，4.2和3.7，对于脆性破坏构件则相应提高0.5，分别为5.2，4.7和4.2.在体系层次，国内外相关规范尚未给出明确规定.国外有学者认为：当体系可靠度指标βsys取4.5时，结构已足够安全［17-18］.规范［13］基于不同体系行为、构件行为和检查水平，建议在役桥梁安全评估的最小目标可靠度βsys取4，但该规定主要针对混凝土桥梁.文献［19］建议钢结构体系可靠度可采用规范［13］中关于构件脆性破坏的设计值，其中安全等级为三级的结构可靠度指标为4.2.文献［10］建议按文献［13］关于构件延性破坏设计安全标准提高一档取用，即βsys最低取4.2.

桥梁施工事故［1-2］多为临时结构设计过于经济造成.考虑到桥梁施工临时结构失效可能造成后果的严重性，而提高临时结构可靠度所增加的投入占桥梁施工总投入的比重较小，因此适当提高临时结构的目标可靠度是可行的.通过对比国内外相关规范关于可靠度指标取值，同时考虑临时结构的安全等级水平，以3.7作为临时结构构件的最低可靠度指标；对于节点连接、锚固等可引起结构瞬间失效的部分，其设计最低可靠度指标取4.2，因此，将临时结构的最低体系可靠度指标取为4.2.

2 随机变量的统计参数

施工中，临时结构的随机性主要来自三个方面：抗力、荷载和人因差错.抗力主要受材料力学特性和结构构造影响；荷载随施工的进行而不断变化；人因差错同施工人员专业技能熟练程度和检查次数有关.

2.1 抗力统计参数

影响结构抗力的主要因素有三个：几何参数的不定性；材料性能的不定性；计算模式的不定性.本文主要针对前两者展开研究，有关计算模式的不定性此处不作赘述.考虑到目前结构（钢结构和混凝土结构）加工、制作以及施工工艺的水平，混凝土结构的离散性和材料不确定性较钢结构偏高，但相关研究认为，对钢结构的几何参数和材料性能的不定性进行统计分析是有意义且必要的［19-21］.

2.1.1 几何参数

文献［19］建议构件的几何尺寸变异系数取1.23%，厚度变异系数取3.5%.文献［20］认为普通加工的钢构件其平均截面特性变异系数为5%，而对于反复利用的钢构件，通常将其截面特性变异系数提升到8%.以临时结构构件的截面面积作为基本变量，考虑构件重复利用以及焊接和端头开孔等的影响，计算中假定构件的截面积存在10%的变异.

2.1.2 材料力学特性

文献［19］按构件的厚度给出常用型号钢材的力学性能随机统计参数，如表1所示.文献［21］基于不同形式的构件破坏试验，得到钢构件的随机性统计参数值和变异系数，其中，Q235轴向受力构件的强度均值为1.112，变异系数为0.122；压弯构件强度均值为1.134，变异系数为0.123.考虑到成品钢材的材质差异较小，建议钢材力学性能的随机变量服从高斯分布，强度均值和变异系数均按文献［21］取用.

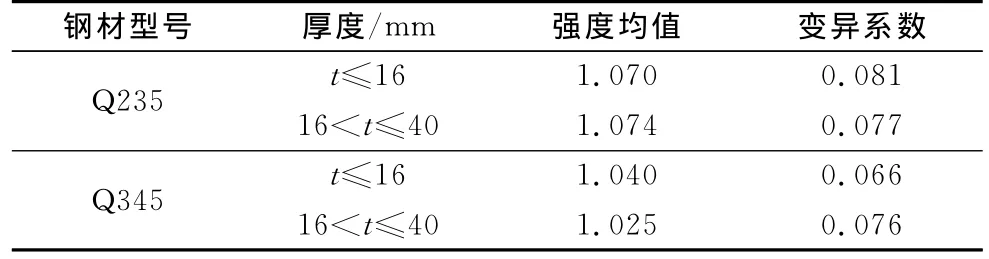
表1 钢材随机统计参数Tab.1 Statistical parameters forsteel

2.2 荷载统计参数

2.2.1 永久荷载

永久荷载主要包括混凝土重量和临时结构自重.规范［15］规定混凝土浇筑阶段，恒载的变异系数取值范围在0.08～0.10之间，文献［3］则建议变异系数取0.05.文献［20］建议混凝土变异系数在0.06～0.09之间，文献［22］基于试验得到现场浇筑构件的偏差系数为1.05，变异系数为0.10.上述参数均服从高斯分布.考虑到目前施工质量的控制状况，计算中混凝土的自重偏差系数取1.00，变异系数按0.05取用，服从高斯分布.临时结构的自重变异性通过截面的变异实现.

2.2.2 可变荷载

施工中可变荷载的取值为混凝土浇筑完毕时刻对应的活载值，文献［23-24］均已对此予以验证.规范［25］规定临时结构的可变荷载标准值为2.0kPa，冲击系数为1.2，则临时结构的实际可变荷载为2.4 kPa，这同澳大利亚混凝土研究所和美国混凝土学会（ACI）对施工阶段可变荷载的规定设计值相同［26］.而文献［26］得出活载均值与名义值比值为0.3.计算中，活载均值取0.72kPa，变异系数取0.7，并服从高斯分布［24］.

桥梁施工中，临时结构不仅承受竖向荷载，还承受风载等横向荷载，特别是跨海跨江的大桥施工中，风荷载较内陆偏大，因此计算中将横向的风荷载考虑在内更贴近临时结构的实际受力状态.计算时，分别考虑施工地区50年一遇和100年一遇的风压值，但不考虑风压的变异性.

2.3 人因差错的统计参数

临时结构在安装、移动等过程中出现结构整体失效的行为多为人因差错所致，因此，临时结构体系可靠性分析时考虑人因差错是必要的.为对人因差错进行量化，有学者曾采用经典的可靠度理论进行求解［27］，但众多可能出现的人因差错使该式的求解十分复杂、困难.另一方面，现存有关人因差错的统计资料极少且较为片面.

文献［27］以对数正态分布作为人因差错率PE的分布模型，其相应的密度函数如下：

式中：ξ与λ为分布函数，分别代表人因差错分布的离散程度和平均水平，反映了由于操作者不同的能力和个性、不同的工作环境以及不同的影响基本操作完成的其他因素所造成的人因差错率的内在变化规律.两个参数同分布的期望值μ、标准差σ以及中值PEm的关系如下：

计算中，按文献［27］的方法考虑人因差错，λ取为0.003［28］.假定所有人因差错只影响临时结构抗力分布的期望值，而不改变其分布的离散性；同时假定所有受人因差错影响的工作在施工前被全面检查两次［27］.

3 算例分析

3.1 工程概况

本工程为一三跨预应力混凝土变截面连续箱梁矮塔斜拉桥，跨径布置为80m+140m+80m.最大悬浇节段箱梁高5.173m，长5.000m，混凝土方量68.7m3.采用对称悬臂施工，要求每节段混凝土一次浇筑完成.

本桥箱梁悬臂施工选用三榀桁架组成的自锚式三角挂篮，挂篮结构如图1所示，所有构件均采用Q235型钢，前、后斜撑、立柱以及主纵梁采用Q345的Φ50钢销连接.图2为三角挂篮的立面受力示意图，其中：A1为主纵梁面积；A2为后斜撑面积；A3为前斜撑面积；A4为立柱面积；A5为上横梁面积（包括前、后两个）；A6为下横梁面积（包括前、后两个）；A7为单根吊带面积；A8代表构件间的节点；P1，P2分别代表前、后上横梁传给主纵梁的荷载.表2为挂篮主要构件及荷载的统计参数及分布状况.

3.2 体系失效模式

挂篮发生倾覆、坠落或部分杆件失效等导致挂篮失效的事件定义为挂篮的失效.本研究基于对三角挂篮失效资料的调研，确定本挂篮可能的失效事件，并给出可能导致该失效事件发生的原因，具体如下：① 倾覆失效，主要为后锚失效；② 桁架失效，主要包括主纵梁、立柱、前拉杆、后拉杆等构件的单独失效和组合失效；③ 横梁失效，分别为四个横梁的单独和组合失效；④ 吊带失效，包括单根吊带失效、相邻两根或非相邻吊带同时失效等.

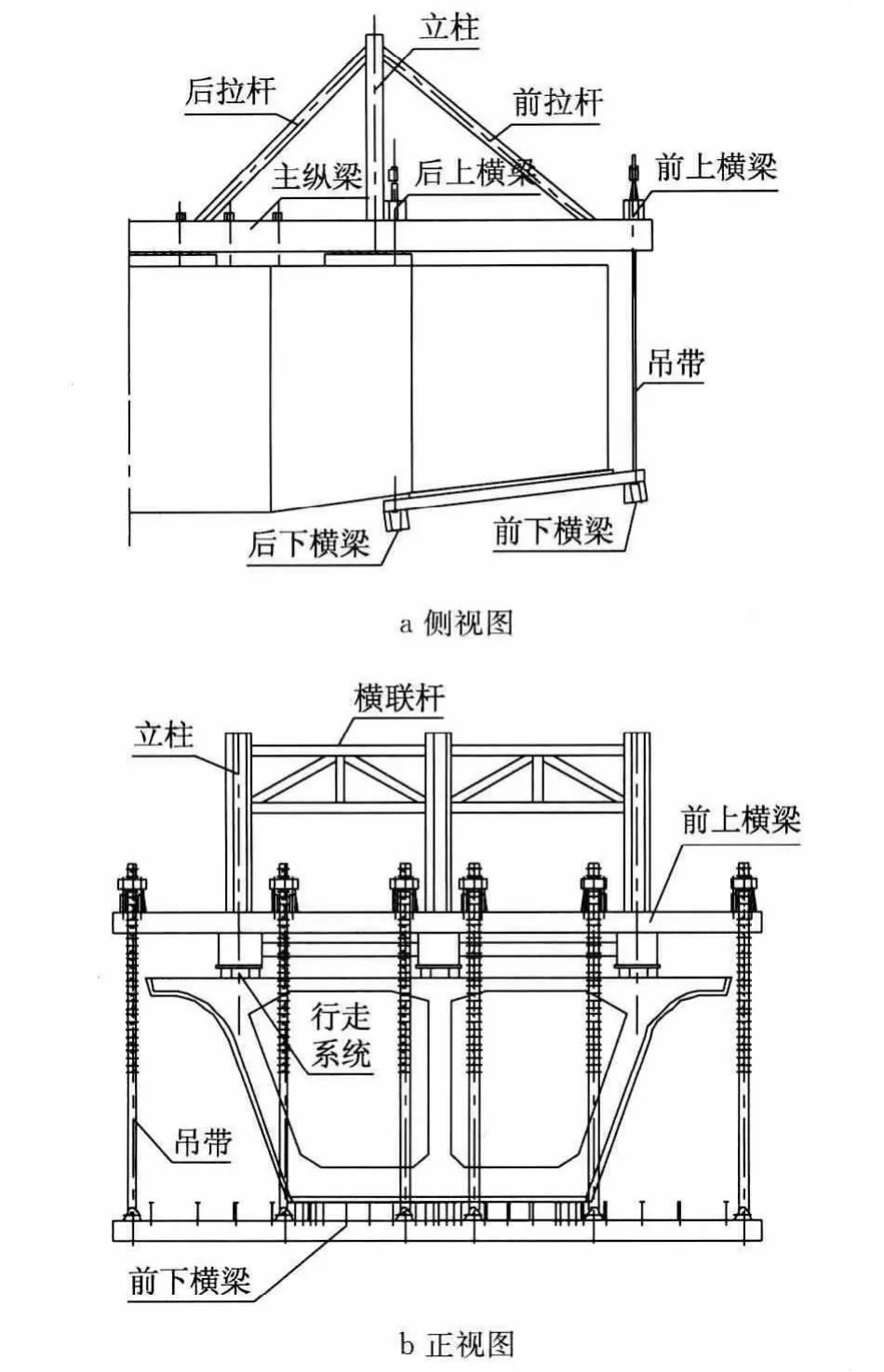
图1 挂篮构造图Fig.1 Structural sketch of the traveler

图2 挂篮受力示意图Fig.2 Mechanical sketch of the traveler

表2 挂篮部分构件及荷载的统计参数Tab.2 Parameters of partial components and loads

通过对上述挂篮失效行为的归并，确定相应的计算工况，采用有限元对本算例挂篮进行计算，基于有限元计算结果并结合串并联模型即可确定本挂篮可能的失效模式.计算中，混凝土节段自重及施工可变荷载按从属面积法施加到底板小纵梁，而风荷载则按挂篮及混凝土节段侧面受风面积计算后分摊到挂篮主桁架上.经计算，本三角挂篮的失效模式可描述如下：① 对于桁架子体系，三榀桁架中任一失效将导致挂篮体系失效，因此，各榀桁架之间应为串联关系.而各榀中只有主纵梁失效才会导致该榀桁架失效；② 对于吊带子体系，任意相邻两吊带失效均会导致吊带子体系的失效，进而引发挂篮体系的失效，因此，吊带子体系的失效模式可看作是任意相连两吊带并联的失效模式；③ 包括上、下横梁等在内的其他构件以及后锚、连接等，任一失效将导致挂篮体系失效，因此，该部分的失效模式均为串联.

综上分析及图3，挂篮结构自身的失效模式便可以确定为桁架、横梁以及吊带等的串联失效模式.并可用下式描述：

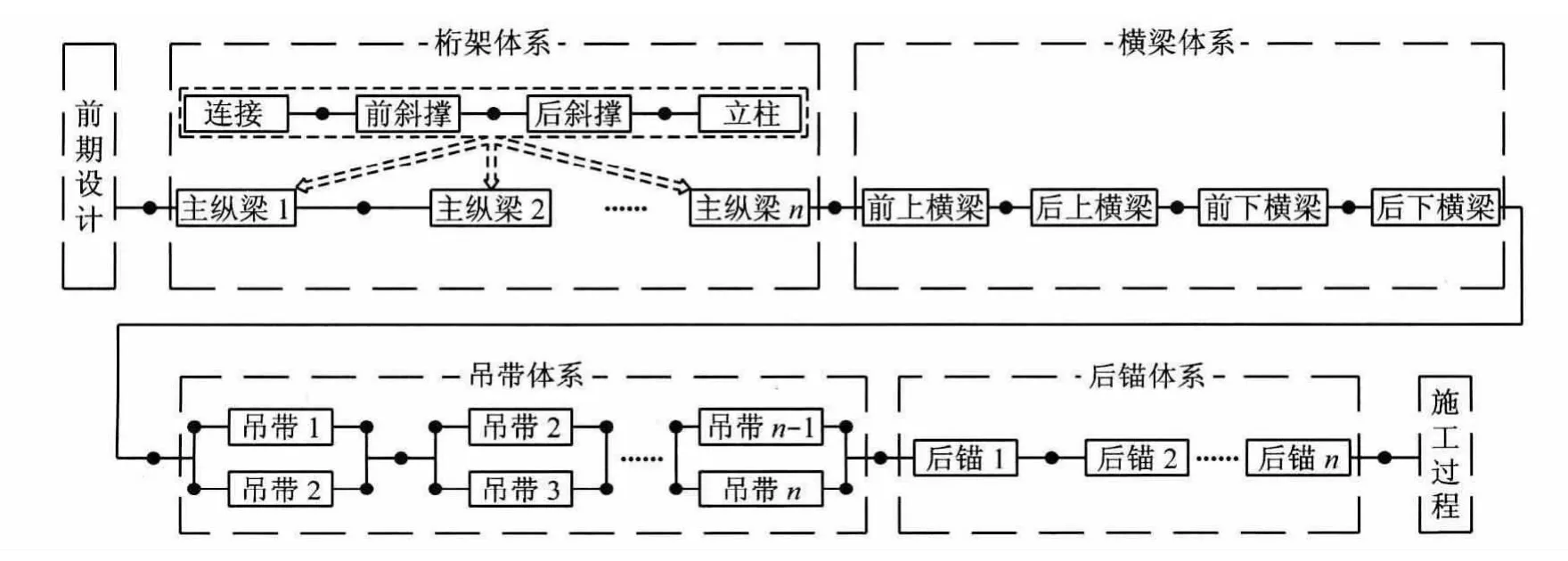
图3 三角挂篮失效模式Fig.3 Failure models of the triangle traveler

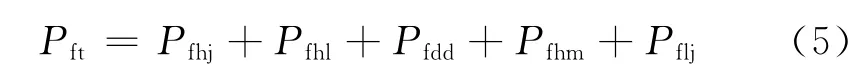
式中：Pfhj为桁架引起的失效；Pfhl为横梁引起的倾覆失效；Pfdd为吊带引起的失效；Pfhm为后锚引起的失效；Pflj为节点连接引起的失效.

3.3 结果分析

3.3.1 构件层次

依据构件的受力形式给出对应的破坏模式，并采用Monte-Carlo抽样法对各构件的可靠度指标β进行计算，结果列于表3.由计算结果可得如下结论：

（1）施工中，挂篮的前斜撑可靠度指标最低，其中，在考虑百年一遇的风载工况下其可靠度指标β=4.566＞3.7，表明挂篮各构件均能较好地满足要求且具有一定的安全储备；

（2）A5（上横梁）的可靠度指标较其他构件的可靠度指标偏高，说明该构件的设计偏于保守，可在保证安全的前提下更换为较小截面的构件；

（3）即使考虑百年一遇风压值时，风荷载对构件的可靠度指标影响仍较小，这是因为同竖向荷载相比横向荷载过小所致.

表3 不同风载作用下挂篮部分构件计算结果Tab.3 Calculation results of components under different wind loads

3.3.2 体系层次

基于前述挂篮失效模式的研究和构件可靠度的计算结果，对算例挂篮的体系进行可靠度计算分析，计算结果列于表4中，由表可得如下结论：

（1）挂篮体系可靠度指标βsys小于最小子体系可靠度指标βmin，这是因为挂篮体系的失效模式是由几个子体系串联而成的失效模式；

（2）不考虑人因差错及风荷载时，挂篮体系可靠度指标βsys=4.509 2，考虑人因差错影响时，βsys=4.227 2，均大于4.2，表明在箱梁正常施工过程中本挂篮安全；

（3）考虑人因差错的βsys较不考虑时显著减小，说明考虑人因差错对临时结构可靠度的影响是必要的；

（4）后锚子体系的可靠度指标较其他子体系可靠度指标偏高，说明该挂篮锚固的设计偏于保守，但考虑到后锚失效可能导致的后果严重性，以及降低该部分可靠度带来的经济指标提高程度较小，建议后锚部分不做调整.

表4 体系可靠度计算结果Tab.4 Calculation results of system reliability

4 结论

（1）采用有限元计算结合串并联失效模型对临时结构的失效模式进行判定的方法容易实现，而采用体系可靠度来评价临时结构的安全性，不仅能够较好地解决施工中抗力和荷载等的不确定性，还能直观反映结构的一致可靠性水平，便于对结构进行优化.

（2）采用体系可靠度对临时结构进行安全性评估的方法，可较好地解决施工过程中抗力和荷载的随机变量问题.建议桥梁施工永久荷载均值取1.0，变异系数取0.05；可变荷载均值取0.3倍名义值，变异系数取0.7.

（3）临时结构体系可靠度指标在考虑人因差错时较不考虑时偏小，且随检查次数的增加而提高，但提高的幅度随检查次数的增加而减小，因此对临时结构进行可靠度分析时考虑人因差错的影响是必要的.

［1］ Hadiprono F，Wang H.Causes of falsework collapses during construction［J］.Structure Safety，1987，4（1）：179.

［2］ Carper K.Structural failures during construction［J］.Journal of Performance of Constructed Facilities 1987，1（3）：132.

［3］ Chan S L，Zhou Z H.Stability analysis of semirigid steel scaffolding［J］.Engineering Structures，1995，17（8）：568.

［4］ Yu W K，Chung K F，Chan S L.Structural instability of multi-storey door-type modular steel scaffolds［J］.Engineering Structures，2004，26（7）：867.

［5］ Liu H，Zhao Q，Wang X，etal.Experimental and analytical studies on the stability of structural steel tube and coupler scaffolds without X-bracing［J］.Engineering Structures，2010，32（4）：1003.

［6］ Charuvisit S，Ohdo K，Hino Y，etal.Risk assessment for scaffolding work in strong winds［C］∥Proceedings 10th International Conference on Structural Safety and Reliability（ICOSSAR’09）：Safety，Reliability and Risk of Structures，Infrastructures and Engineering systems.［S.l］：CRC Press，2010：1-10.

［7］ Epaarachchi D C，Stewart M G，Rosowsky D V.Structural reliability of multistory buildings during construction［J］.Journal of Structural Engineering，2002，128（2）：205.

［8］ Epaarachchi D C，Stewart M G.Human error and reliability of multistory reinforced-concrete building construction［J］.Journal of Performance of Constructed Facilities，2004，18（1）：12.

［9］ Zhang H，Rasmussen K J R，Ellingwood B R.Reliability assessment of steel scaffold shoring structures for concrete formwork［J］.Engineering Structures，2012，36（3）：81.

［10］ 刘玉姝，李国强.平面钢框架结构的整体可靠度设计［J］.同济大学学报：自然科学版，2005，33（8）：1017.LIU Yushu，LI Guoqiang.Reliability-based integrated design of planar steel frame［J］.Journal of Tongji University：Natural Science，2005，33（8）：1017.

［11］ Akgül F，Frangopol D M.Lifetime performance analysis of existing prestressed concrete bridge superstructures［J］.Journal of Structural Engineering，2004，130（12）：1889.

［12］ Imai K，Frangopol D M.Reliability-based assessment of suspension bridges：application to the Innoshima Bridge［J］.Journal of Bridge Engineering，2001，6（6）：398.

［13］ 王晓明.在役多梁式RC简支桥体系时变可靠度评估方法与关键问题［D］.上海：同济大学，2011.WANG Xiaoming.The time-dependent system reliability assessment method and key issues for existing multi-beam RC simply supported bridges［D］.Shanghai：Tongji University，2011.

［14］ Canadian Standards Association.CAN/CSA-S6-00Canadian highway bridge design code［S］.Toronto：Canadian Standards Association，2000.

［15］ AASHTO.LRFD bridge design specifications［S］.Washington D C：AASHTO，2007.

［16］ 中华人民共和国建设部.GB50283—1999公路工程结构可靠度设计统一标准［S］.北京：中国建筑工业出版社，2001.Ministry of Construction of the People’s Republic of China.GB50283-1999 Unified standard for reliability design of highway engineering structures ［S］.Beijing： China Architecture and Building Press，1999.

［17］ Sexsmith R，Reid S.Safety factors for bridge falsework by risk management［J］.Structural Safety，2003，25（5）：227.

［18］ Casas J.Reliability-based partial safety factors in cantilever construction of concrete bridges ［J］.ASCE Journal of Structural Engineering，1997，123（3）：305.

［19］ 李国强，刘玉姝，赵欣.钢结构框架体系高等分析与系统可靠度设计［M］.北京：中国建筑工业出版社，2006.LI Guoqiang，LIU Yushu，ZHAO Xin.Advanced analysis and systemic reliability design for steel framed systems ［M］.Beijing：China Architecture and Building Press，2006.

［20］ Ellingwood B， MacGregor J G，Galambos T V，etal.Probability based load criteria：load factors and load combinations［J］.Journal of the Structural Division，1982，108（5）：978.

［21］ 陈绍蕃，顾强.钢结构［M］.北京：中国建筑工业出版社，2007.CHEN Shaofan，GU Qiang.Steel structure［M］.Beijing：China Architecture and Building Press，2007.

［22］ Tabsh S W.Nowak A S.Reliability of highway girder bridges［J］.Journal of Structural Engineering，1991，177（8）：2372.

［23］ Fattal S.Evaluation of construction loads in multistory concrete buildings，NBS building science series 146［M］.Washington D C：National Bureau of Standards，1983.

［24］ Ikaheimonen J.Construction loads on shores and stability of horizontal formworks ［D］.Stockholm：Royal Institute of Technology，1997.

［25］ 中华人民共和国建议部.GB50009—2001建筑结构荷载规范［S］.北京：中国建筑工业出版社，2001.Ministry of National Defense of the People’s Republic of China GB50009—2001 Load code for design of building structures［S］.Beijing：China Architecture and Building Press，2001.

［26］ Hao Zhang，Kim J，Bruce R.Reliability assessment of steel scaffold shoring structures for concrete formwork ［J］.Engineering Structures，2012，36（3）：81.

［27］ 徐茂波，徐峰，刘西拉.混凝土结构施工中人因差错的模拟［J］.中国安全科学学报，2007，17（5）：9.XU Maobo，XU Feng，LIU Xila.Simulation of human errors during construction of concrete structure ［J］.China Safety Science Journal，2007，17（5）：9.

［28］ Park K S.Human reliability：analysis，prediction，prevention of human errors［M］.Amsterdam：Elsevier Science Publishers，1987.