一种基于数值流形法的模拟岩体结构面新方法

李恩璞，蔡永昌，李耀基，朱合华

（1.同济大学 土木工程学院，上海200092；2.同济大学 岩土及地下工程教育部重点实验室，上海200092；3.云南磷化集团有限公司，云南 昆明650600）

岩土工程中经常遇到含各种结构面（如节理、裂隙和软弱夹层等）的岩体，在分析岩体的变形和应力演化时必须考虑结构面对岩体工程力学性质的严重影响.目前对于这类不连续结构面的处理方法主要有两大类：第一类是把岩体结构看成是由软弱结构面切割而成的一系列岩块所组成的，如离散单元法（DEM）［1］、块体理论［2］、不连续变形分析（DDA）［3］等；第二类则是以有限单元法（FEM）为基础，引入能反映岩体结构不连续性的模型，如节理单元法（Goodman Element）［4］以及用于模拟多节理岩体的等效连续体模型［5］和损伤模型［6］等.

DEM，DDA等非连续分析方法将岩体抽象为完全非连续的离散介质或块体，可以较方便地模拟岩体工程失效破坏的全过程，其计算能力和分析效果正逐渐得到认同与肯定.但在分析大规模岩体工程时，其离散块体的几何形态分布、接触嵌入算法、计算耗时等问题的存在，较大地限制了该类方法的实际工程应用.

以有限元法为基础的连续介质方法，可采用Goodman单元来模拟需重点关注的几条宏观控制性断层节理或软弱夹层，更具实际应用价值，但是由于有限单元法单元协调性的要求，在复杂的岩体工程建模时会带来极大的困难.例如，图1所示的某水电边坡有限元分析模型，其单元网格必须要与开挖卸荷边界、材料边界、节理断层等不连续边界相协调，很容易产生会带来较大误差的畸形有限单元.当采用Goodman单元等模拟断层节理的错动变形时，如果出现两条或多条交叉节理断层，在交叉处需要设置多个不同的结点正确模拟节理断层的独立变形；当考虑节理裂隙的破坏扩展时，有限单元则需要在节理裂隙的扩展过程中采用复杂的重构算法不断更新计算网格.

图1 某水电站侧面边坡局部剖面图Fig.1 Section view of part of a hydropower station slope

针对节理岩体这种既有连续又有非连续的特性，石根华博士［7］在1992年提出了一种更为一般的可以同时处理连续与非连续的统一计算方法——数值流形方法（NMM）.流形方法自提出以来，就倍受关注，在流形覆盖生成［8-10］、裂纹扩展模拟［11］、三维数值流形理论［12-13］、实际岩土工程应用［14-16］等方面取得了较多的结果，关于流形方法更多的最新研究进展可参见文献［17-18］.

本文利用数值流形方法可以有效地统一处理连续和非连续变形问题的优点，借鉴Goodman单元的相关理论，提出了数值流形方法中节理、断层和软弱夹层等岩体结构面的模拟处理新方法，极大地简化了含岩体结构面的复杂岩体工程的前处理及分析过程.算例结果表明了该方法的正确性和有效性.

1 流形方法的有限覆盖系统

1.1 覆盖系统的自动生成

考虑任意区域Ω（如图2所示），其中含两条物理线1和2.在流形方法中，材料不连续面（如节理、裂纹等）被称作物理线.

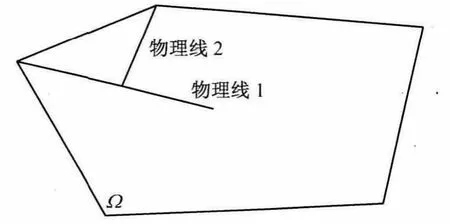
图2 含两条物理线的任意区域Fig.2 An arbitrary domain with two physical lines

流形方法中有限覆盖（即物理覆盖）生成的框架如下：

（1）与有限单元法类似，用三角形网格划分问题域，作为数学网格如图3所示.在该过程中可以不用考虑物理线的存在.

图3 区域Ω的数学网格Fig.3 The mathematical mesh used forΩ

（2）生成数学覆盖和数学单元.对于每个结点i，定义那些以该结点i作为顶点的所有三角形单元的总和为一个数学覆盖，如图4所示.

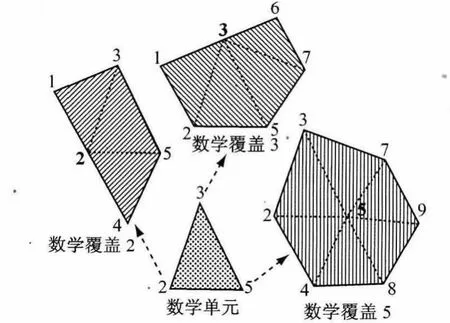
图4 数学覆盖和数学单元Fig.4 The definition of mathematical covers and elements.

（3）用物理线分割数学覆盖，如图5所示.

（4）物理覆盖就是物理线与数学覆盖的交集，如图6所示.

（5）最后生成的整个区域Ω的有限覆盖如图7所示.

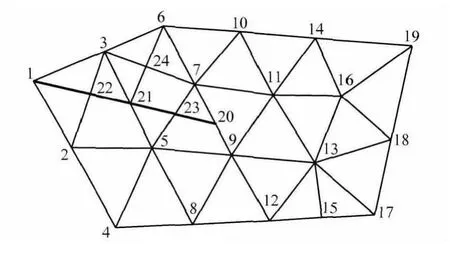
图5 物理线分割数学网格Fig.5 The partitioning of a mathematical mesh by the physical lines

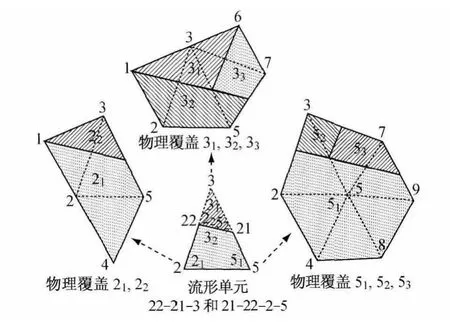
图6 物理覆盖和流形单元Fig.6 The sample physical covers and manifold elements

图7 区域Ω的有限覆盖Fig.7 The finite covers for domainΩ

1.2 流形单元上的位移插值函数

三角形流形单元上的位移场函数可按如下方式构造，仅取x方向为例，y方向可以同样的过程获得.例如图6中的流形单元21-22-2-5，其x方向的位移场函数为

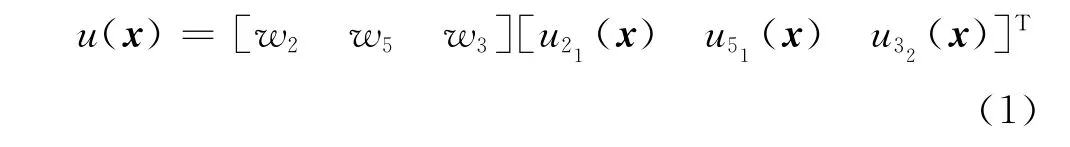
其中，对二维情形x=（x，y）；w2，w5和w3是权函数，此处取三结点三角形有限元的形函数作为权函数，按下式计算：

需要指出的是，式（1）中的u21（x），u51（x）和u32（x）并不是有限单元法中的结点位移，而是定义在物理覆盖21，51和32上的局部覆盖函数（图6），可以取为常量、多项式级数或局部解析解等形式.在本文中，物理覆盖的局部位移函数取为常量形式.

同样的方法可以构造出图6中的流形单元22-21-3上x方向的位移场函数为

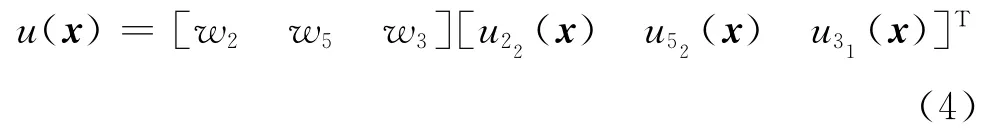
从式（1）和（4）可以看出，流形方法在保持数学网格不变的情况下，采用独立的物理覆盖自由度即可以很容易地实现各种不连续性的模拟.

1.3 控制方程的形成

在确定了流形单元的位移函数之后，类似于有限元，可以方便地利用几何方程和物理方程求得单元的应力和应变.流形方法中的控制方程仍可以建立在系统最小势能原理的基础上，对总势能取一阶变分即可导出系统的整体平衡方程.

2 岩体结构面模拟新方法

对于“张开型”的岩体结构面，假设结构面不能抗拉时（图8a），由于流形方法的双重网格特点，在保持数学网格不变的情况下，其结构面两侧采用不同的物理覆盖和局部覆盖函数，可以实现不连续面处的自由分开和移动，能够自然、方便地实现模拟此种类型的结构面（见前节所述）.

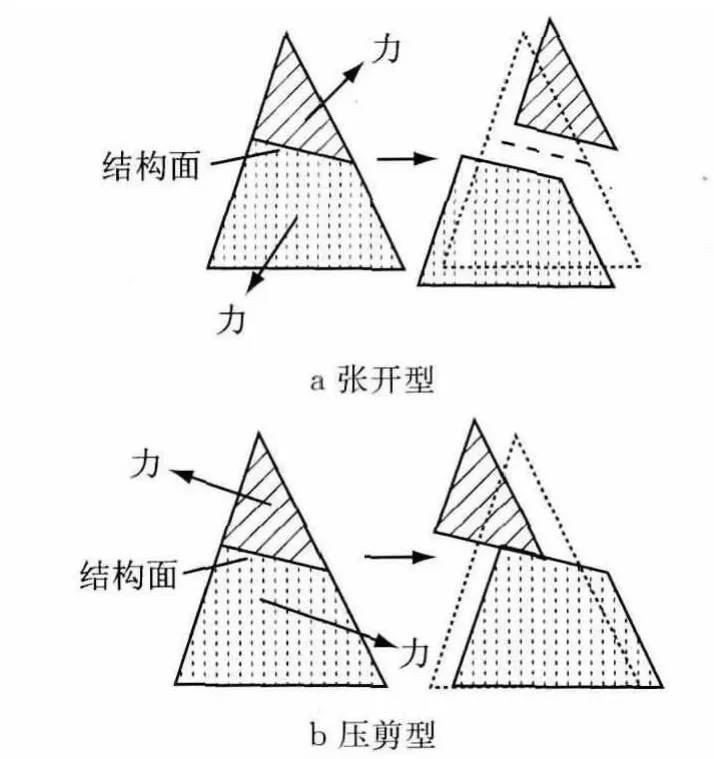
图8 两种结构面类型Fig.8 Two kinds of discontinuities

而对于“压剪型”或具有抗拉强度的“张开型”岩体结构面，需要考虑结构面上的接触和摩擦（图8b），大致可以分为如下两种情形：①已知结构面的切向和法向刚度系数（ks和kn）的无厚岩体结构面；②已知结构面的厚度、弹性模量（E）和剪切模量（G）的软弱岩体结构面.

可以分别借鉴有限元法中的Goodman无厚节理单元和软弱夹层单元相关理论来进行分析模拟，但是在流形方法里所构造的节理单元或夹层单元的4个结点不需要像有限元法一样必须是单元的结点，从而大幅度减少了其前处理的复杂度.本文结合数值流形方法的基本理论，提出了一种岩体结构面的处理新方法，其实现过程如下.

2.1 无厚岩体结构面

在如图7所示的覆盖系统基础上，再对物理线进行n等分，并在两个方向上分别偏移一个微小的距离λ和η以建立节理单元，如图9所示.其中等分物理线的长度为d（取为所有数学单元平均边长的一半），偏移距离λ=αd，η=βd.该偏移距离只是为了数值流形方法处理方便而虚拟引入的，当其取值较小时（例如α或β取0.001～0.01），对计算结果的影响可以忽略不计.

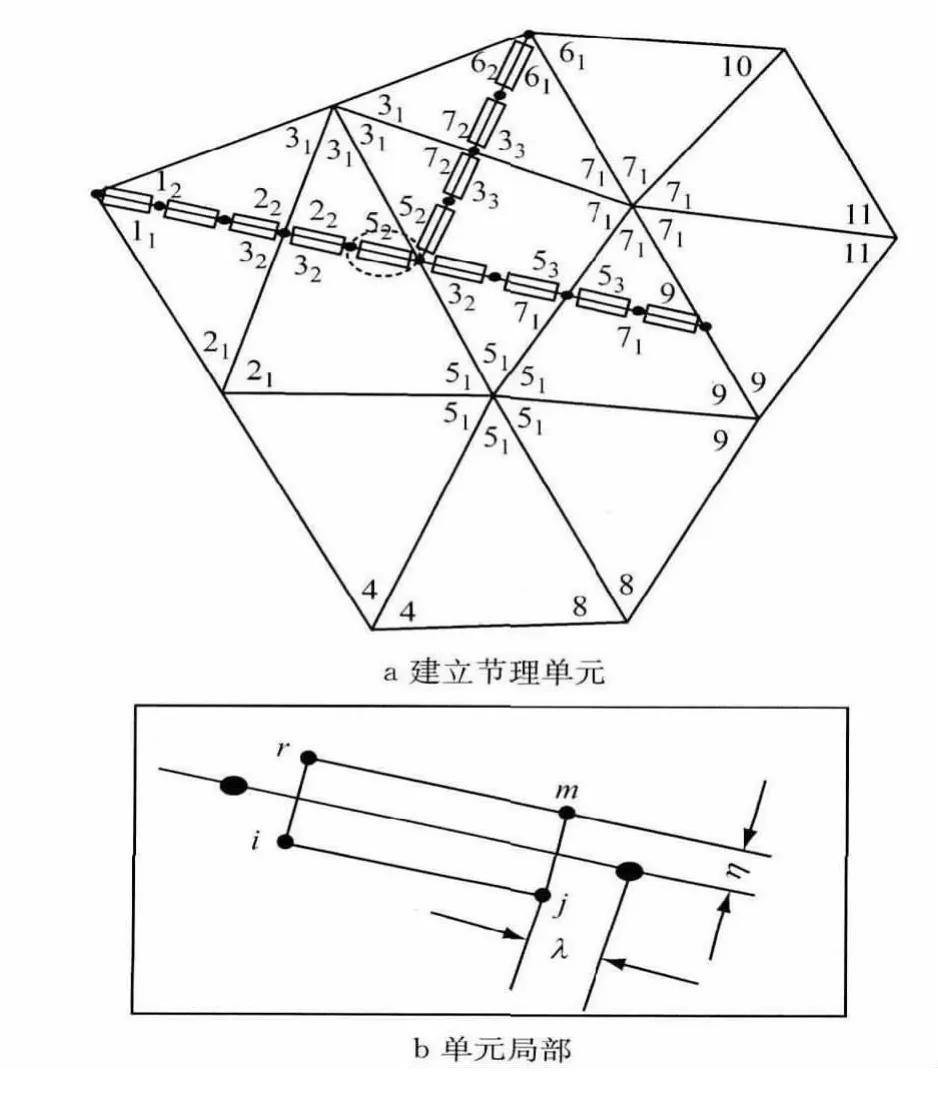
图9 物理线的处理方法Fig.9 The dealing with physical lines

以节理单元ijmr为例，它的局部坐标系如图10所示，其4个结点都处于数学单元2-5-3，结点i，j处于物理覆盖21-51-32，结点m，r处于物理覆盖22-52-31，它们在x方向的位移函数可表示为

从式（9）可以看出，i，j，m，r4个结点不需要是数学单元（对应有限单元法的有限单元）的结点，而是为了模拟不连续结构面虚拟的，故其数值实施时极为方便.

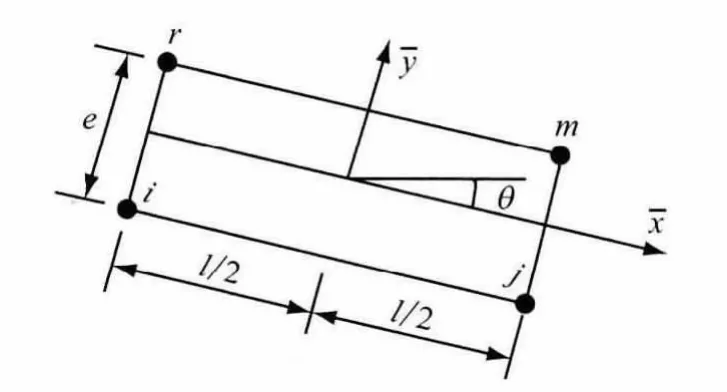
图10 节理单元Fig.10 Joint elements

假设图10的节理单元上缘rm和下缘ij上的位移是线性分布的，则该单元上下缘的水平位移差可表示为

式中

由于式（16）的节理单元刚度矩阵在局部坐标系下定义，在组集到整体刚度矩阵之前，需要把该表达式坐标转换到整体坐标系下，其转换和组集的过程与有限单元法类似.

2.2 软弱岩体结构面

当已知结构面的厚度（e）、E和G时，可按朱伯芳提出的软弱夹层单元［19］思路处理，其位移函数构造方法与上述无厚节理单元相同，只需令

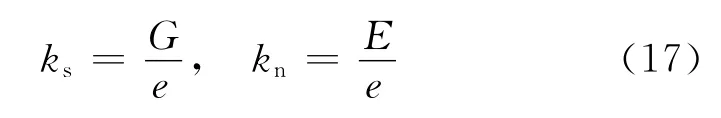
即可按照上述同样的过程进行计算.

3 算例验证

3.1 含有结构面的标准算例

如图11a所示含结构面的直梁，梁的尺寸宽W=1.0m，长L=8.0m，结构面位置a=3.1m，在末端受到水平方向的均布拉应力σ=1.0MPa.取材料的弹性模量E=10.0MPa，泊松比μ=0.25，以平面应力问题处理，不计自重.

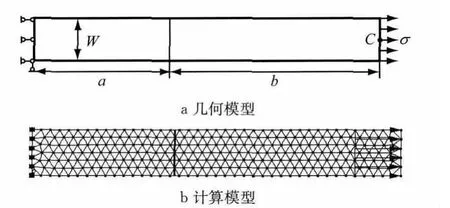
图11 含结构面直梁Fig.11 Straight beam with discontinuity

采用如图11b所示的282个结点的三角形网格作为流形方法的数学网格，在划分三角形数学网格时，可以不考虑结构面的存在.对应图9的等分结构面的长度取为d=0.179，偏移距离系数取为α=0.01，β=0.01.取结构面的刚度系数ks=1.0MPa，当kn从1.0～1 000.0MPa变化时，直梁最右端中点C处水平位移的数值解与理论解的比较如表1所示.可以看出，本文方法能够较方便、准确地进行各类结构面的分析计算.

设ks=1.0MPa，kn=1 000.0MPa.当偏移系数α=0.01，β取不同值时，C点的水平位移数值解如表2所示；当偏移系数β=0.01，α取不同值时，C点的水平位移数值解如表3所示.从表2和表3可以看出，α或β的不同取值对计算结果的影响不敏感.大量计算实例表明，通常α或β取为0.01即可获得满意的计算结果.

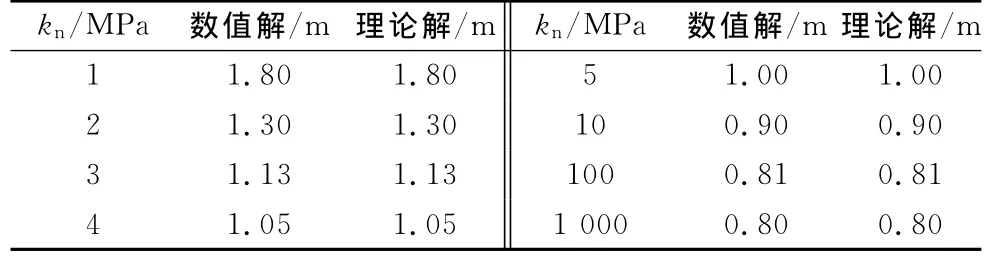
表1 直梁C点处数值解与理论解的水平位移比较Tab.1 The comparison of numerical and analytical solutions at point C

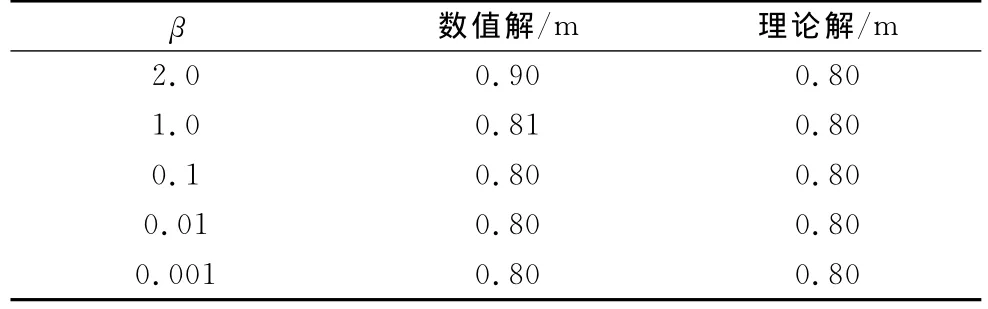
表2 β取不同值时C点的水平位移Tab.2 The displacement at point C with differentβ

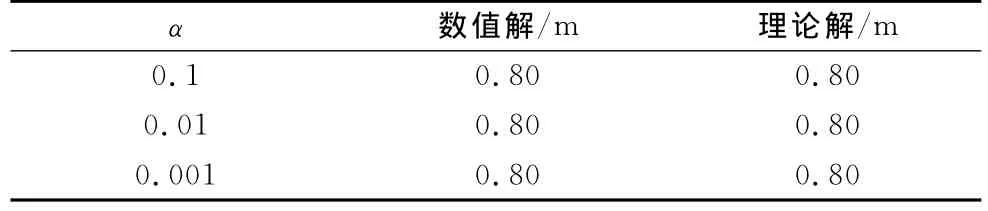
表3 α取不同值时C点的水平位移Tab.3 The displacement at point C with differentα

3.2 含单一节理岩质边坡

取自文献［20］的连通率为100%的岩质边坡，如图12所示，其岩体及节理参数见表4.其中，γ为重度，E为弹性模量，μ为泊松比，c为黏聚力，φ为内摩擦角.采用本文的无厚节理单元模拟节理，节理单元刚度系数取为ks=1.93×106kPa，kn=5.0×106kPa.

对于本算例，采用RFPA程序得到的边坡安全系数为1.000，滑裂面就是边坡的节理面，如图13所示［20］.采用如图14所示的444个结点的三角形网格作为流形方法的数学网格，利用本文方法结合图论边坡滑移面搜索算法［21］得到的边坡最小安全系数为1.020，得到的最危险滑移面是沿着贯通节理面，与文献［20］的对照解结果吻合良好.

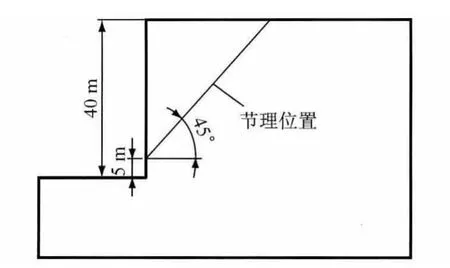
图12 岩质边坡示意图Fig.12 Sketch of rock slope

表4 岩体及节理材料参数Tab.4 Material parameters of rock mass and joint

图13 RFPA计算结果Fig.13 Results by RFPA

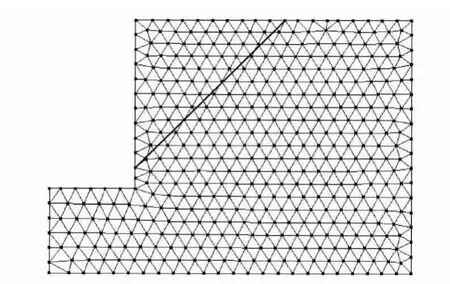
图14 本文方法计算得到的滑移面Fig.14 Slip surface by the proposed method

3.3 某水电站岩石高边坡稳定性分析

如图15所示的某水电站岩石高边坡，依据地质资料保留了对边坡稳定性起主要影响的节理，从边坡表面至边坡深部的岩土类别依次为强卸荷带S1和弱卸荷带 W1，并存在着交叉的结构面g10.岩层及节理面的材料参数如表5所示，节理单元刚度系数取为ks=5.56×105kPa，kn=1.5×106kPa.计算范围水平方向取500m，高度方向取335m.

采用2 613个结点的三角形网格作为流形方法的数学网格，利用本文方法结合图论边坡滑移面搜索算法［21］得到的边坡最小安全系数为1.060，其搜索得到滑移面形状如图16所示.

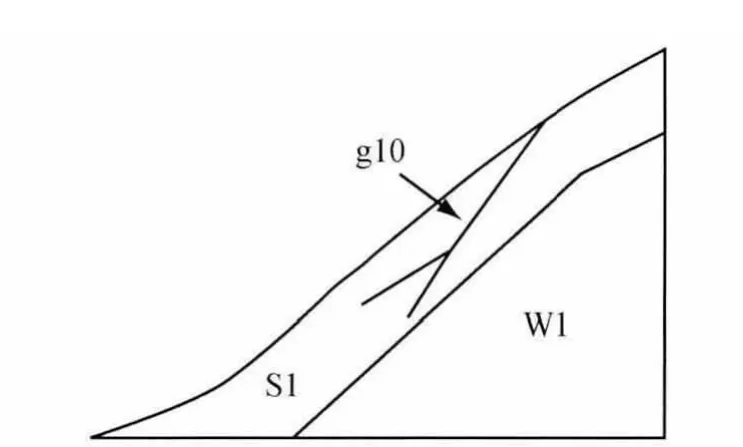
图15 高边坡计算模型图Fig.15 The calculation model of high slope

表5 高边坡材料参数Tab.5 The material parameters of high slope

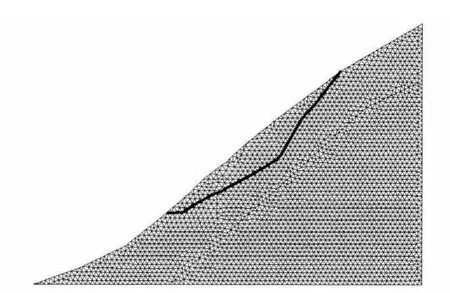
图16 高边坡的滑移面形状Fig.16 The slip plane shape of high slope

4 结论

本文在数值流形方法基础上，提出了一种适合于节理、断层和软弱夹层等岩体结构面的模拟处理新方法，极大简化了含岩体结构面的复杂岩体工程的前处理及分析过程，在岩体工程分析中具有广阔的应用前景.本文所使用的计算理论仍然为石根华提出的数值流形方法.从流形方法的基本理论可以看出，其计算效率与有限元方法大致相当，但是由于数值流形方法中节理、断层等切割岩体后，在流形覆盖的生成等方面付出了相应的代价，从而获得了连续和非连续统一分析的便利.

论文目前仅仅探讨了二维弹性问题的分析求解，将其扩展到非线性或三维问题是完全可行的，这也将是作者下一步的工作.

［1］ Cundall P A.A computer model for simulating progressive large-scale movements in blocky rock systems ［C］//Proceedings of the Symposium of the International Society of Rock Mechanics.Nancy：［s.n.］，1971：11-18.

［2］ Goodman R E，Shi G H.Block theory and its application to rock engineering［M］.［S.l.］：Prentice-Hall，1985.

［3］ Shi G H，Goodman R E.Discontinuous deformation analysis［C］//Proceedings of 25 US Symposium on Rock Mechanics.［S.l.］：American Rock Mechanics Association，1984：269-277.

［4］ Goodman R E，Taylor R，Brekke T L.A model for the mechanics of jointed rock［J］.Journal of the Soil Mechanics and Foundations Division，1968，14（3）：637.

［5］ Gerard C.M.Elastic models of rock masses having one，two，three sets of joints［J］.International Journal of Rock Mechanics and Mining Engineering Science，1982，19（1）：312.

［6］ Kyoya T，Ichikawa Y，Kawamoto T.A damage mechanics theory for discontinuous rock mass［C］//Proceedings of 5 International Conference Numerical Method in Geomechanics.Nagoya：［s.n.］，1985：469-480.

［7］ Shi G H.Modeling rock joints and blocks by manifold method［C］// Proceedings of 32nd US Symposium on Rock Mechanics.New Mexico：［s.n.］，1992：639-648.

［8］ Cai Y C，Zhuang X Y，Zhu H H.A generalized and efficient method for finite cover generation in the numerical manifold method［J］.International Journal of Computational Methods，2013，DOI：10.1142/S021987621350028X.

［9］ Cai Y C，Wu J，Atluri S N.A new implementation of the numerical manifold method（NMM）for the modeling of noncollinear and intersecting cracks［J］.Computer Modeling in Engineering and Sciences，2013，92（1）：63.

［10］ 武杰，蔡永昌.基于四边形网格的流形方法覆盖系统生成算法［J］.同济大学学报：自然科学版，2013，41（5）：641.WU Jie，CAI Yongchang.Generation algorithm of the cover system in manifold method with quadrangular meshes ［J］.Journal of Tongji University：Natural Science，2013，41（5）：641.

［11］ Wu Z J， Wong L N Y.Frictional crack initiation and propagation analysis using the numerical manifold method［J］.Computers and Geotechnics，2011，39：38.

［12］ Jiang Q H，Zhou C B，Li D Q.A three-dimensional numerical manifold method based on tetrahedral meshes［J］.Computers and Structures，2009，87（13/14）：880.

［13］ 李海枫，张国新，石根华.流形切割及有限元网格覆盖下的三维流形单元生成［J］.岩石力学与工程学报，2010，29（4）：731.LI Haifeng，ZHANG Guoxin，SHI Genhua.Manifold cut and generation of three-dimensional element under fem mesh cover［J］.Chinese Journal of Rock Mechanics and Engineering，2010，29（4）：731

［14］ 焦健，乔春生，徐干成.开挖模拟在数值流形方法中的实现［J］.岩土力学，2010，31（9）：2951.JIAO Jian，QIAO Chunsleng，XU Gandeng.Simulation of excavation in numerical manifold method［J］.Rock and Soil Mechanics，2010，31（9）：2951.

［15］ 王芝银，王思敬，杨志法.岩体大变形分析的流形方法［J］.岩石力学与工程学报，1997，16（5）：199.WANG Zhiyin，WANG Sijing，YANG Zhifa.Large deformation of rock mass with numerical manifold method ［J］.Journal of Rock Mechanics and Engineering，1997，16（5）：199.

［16］ Ning Y J，An X M，Ma G W.Footwall slope stability analysis with the numerical manifold method［J］.International Journal of Rock Mechanics and Mining Sciences，2011，48：964.

［17］ Ma G W，An X M，He L.The numerical manifold method：a review ［J］.International Journal of Computational Methods，2010，7（1）：1.

［18］ 王芝银，李云鹏.数值流形方法及其研究进展［J］.力学进展，2003，33（2）：261.WANG Zhiyin，LI Yunpeng.Numerical manifold method and its development［J］.Advances in Mechanics，2003，33（2）：261.

［19］ 朱伯芳.有限单元法原理与应用［M］.北京：中国水利水电出版社，1998.ZHU Bofang.The finite element theory and applications［M］.Beijing：China Water Power Press，1998.

［20］ 李连崇，唐春安，刑军，等.节理岩体边坡变形破坏的RFPA分析［J］.东北大学学报：自然科学版，2006，21（5）：559.LI Lianchong，TANG Chun’an，XING Jun，etal.Numerical simulation and analysis of deformation and failure of jointed rock slopes by RFPA-Slope ［J］.Journal of Northeastern University：Natural Science，2006，21（5）：559.

［21］ 郑文博.边坡稳定性分析方法研究［D］.上海：同济大学，2013.ZHENG Wenbo.Research on slope stability analysis method［D］.Shanghai：Tongji University，2013.