基于水动力模型和遗传算法的梯级泵站优化调度研究

吴昊，周志华，高英，李继明

（1.天津市水利科学研究院，天津300061；2.天津市引滦工程管理处，天津301900）

基于水动力模型和遗传算法的梯级泵站优化调度研究

吴昊1，周志华1，高英2，李继明2

（1.天津市水利科学研究院，天津300061；2.天津市引滦工程管理处，天津301900）

引滦入津输水沿线采用梯级泵站级联提水的方式工作。为降低泵站系统总能耗，在分析研究梯级泵站输水特点的基础上，设计出梯级泵站站间水位优化结合各单级泵站站内机组优化的调度方法，并利用丹麦DHI MIKE11水动力模型和遗传算法分别建立了河道水位数学模型和泵站优化调度模型，根据各泵站机组实测运行记录，拟合了机组运行效能曲线来计算功耗。结合2011年该梯级泵站运行实测数据，验证了该调度方法的合理性、有效性，能够满足梯级泵站节能降耗的要求。

梯级泵站优化调度；水动力模型；遗传算法；效能曲线

引滦入津输水工程全线通过多个泵站级联提水进行输水调度，在输水过程中，泵站系统效率低、能耗大、运行费用高仍是亟待解决的重要问题。梯级泵站是一个复杂的提水系统，站与站之间的流量、水位相互影响相互制约，各泵站内部又有多台机组共同工作。梯级泵站优化调度涉及泵站之间水力学要素的优化组合和各级泵站站内的机组运行优化，因此需对整个调水系统进行统一的控制和调度。

1 模型建立

1.1 梯级泵站级间水位组合优化

图1为一个n级泵站运行示意图。H11、H21、…、Hn1分别为一级泵站、二级泵站、n级泵站的前池水位，H12、H22、…、Hn2分别为相应的各级泵站后池水位。在输水过程中，第一级泵站前池水位（H11）和第n级泵站后池水位（Hn2）为固定值，即梯级泵站系统总扬程保持不变。第n级泵站扬程由Hn1∈[Hn1min，Hn1max]决定，当第n级泵站的前池水位给定时，第n-1级泵站的后池水位可以通过水力学方法计算求得，以此类推，每一组不同的[H21、H31、…、Hn1]组合决定了各级泵站每次不同的扬程分配，其中必有一组[H21、H31、…、Hn1]对应的梯级泵站系统总能耗最小，此即为所求的梯级泵站最优调蓄水位组合。

图1 n级泵站系统运行示意

1.2 梯级泵站各站内机组工况优化

单个泵站内各机组在同一工况下扬程一致，各单级泵站优化问题即为寻求最优机组组合，并在机组输水总量确定的前提下优化各机组最优流量分配及工作叶角角度，使得在该机组组合下完成工况任务耗能最少。根据机组输水总量及单个机组输水量和功率上限计算出所需最少开机台数，根据排列组合算法计算各机组组合情况下机组耗能；对某一机组组合情况下能耗的计算采用遗传算法，取各机组流量分配为基因，依据测得的各机组效能曲线计算功率，通过遗传算法优选出各机组最优流量分配，使得机组总能耗最小。

2 利用水动力模型计算、优化梯级泵站站间水位

引滦入津输水沿线有闸门、泵站、暗渠管道等众多水工建筑物，泵站间还有分水任务，水流运动复杂。MIKE 11是成熟先进的水环境模型，利用其中的水动力模块（MIKE 11 HD）计算泵站间河道水位。MIKE 11 HD模型基于一维非恒定流圣维南方程组来模拟河流或河口的水流状态。

连续方程为：

动量方程为：

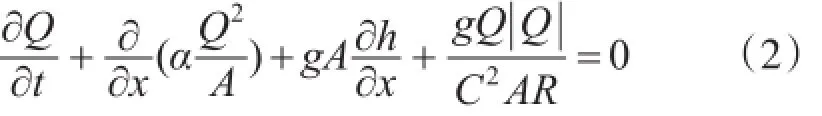
式中：t为时间坐标（s）；x为空间坐标（m）；A为过流断面面积（m2）；Q为流量（m3/s）；h为水位（m）；q为旁侧入流流量（m3/s）；C为谢才系数；R为水力半径（m）；α为动量校正系数；g为重力加速度（m/s2）。

河道水位模型的建立需要大量的基础数据作为支撑，主要包括断面地形数据、水文数据以及主要泵站的抽水流量等，通过对这些数据的加工、分析、处理形成以下文件：①河网文件，用于描述流域，包括河网形状、河道连接关系和水工建筑物的基本设计参数及调度运行规则等；②断面文件，用于描述河道和河滩地形，包括设置河床断面和河滩地形资料等；③边界文件，包括设置模型边界处的流量、水位，取水、引水点的流量等；④参数文件，包括初始条件、糙率设置、输出结果设置等。然后根据引滦入津输水线路的实际水情和工情的特点，建立能够反映引滦输水线路河道水量、水位时空变化规律的数学模型。

引滦入津输水沿线建有潮白河、尔王庄、大张庄3级提升泵站。根据泵站本身建设指标及多年运行经验，各级泵站前、后池水位变化范围及水位调节精度有限，选取最优运行水位时可采用枚举法在各级泵站前池水位的允许范围[Hmin，Hmax]内进行搜索，确定了各级泵站扬程之后再利用遗传算法进行泵站站内优化计算，通过比较确定梯级泵站最优运行方案。

3 利用遗传算法优化各单级泵站运行工况

遗传算法[1-3]是模拟自然界生物进化过程与机制，能以较大概率收敛于问题的全局最优解的一种智能优化算法，基本步骤如下：①选择编码策略，将参数集合转换至位串空间；②定义适应值函数；③确定遗传操作方法和参数，包括种群大小，选择、交叉、变异方法及相应概率；④种群初始化；⑤计算种群适应值；⑥按照遗传策略，运用选择、交叉、变异、保存算子作用于种群并产生下一代群体；⑦判断种群性能，若达到最优状态则结束，若非最优则返回第（6）步。

根据泵站工况优化具体情况，对遗传算法涉及的主要操作及参数选取处理如下：①参数编码采用浮点编码，染色体基因取各机组分配流量，基因个数由机组开机台数确定，初始母体群的产生取各机组流量分配均值。②适应度函数建立采用泵站机组总功率值，并增加各机组功率上限的约束条件。③选择策略采用标准化几何分布规律计算个体遗传概率，采用轮盘赌算法选择优良个体保存。④交叉运算是指对两个相互配对的染色体依据交叉概率（Pc）按某种方式相互交换其部分基因，从而形成两个新的个体。泵站机组优化调度模型中交叉算子采用算术交叉算子。⑤变异运算是指依据变异概率（Pm）将个体编码串中的某些基因值用其他基因值来替换，从而形成一个新的个体。对于采取浮点数编码的个体，某一变异点处的基因值范围为[Xmin，Xmax]，变异运算就是用该范围内的一个随机数去替换原有的基因值。⑥最优保存，遗传算法中选择、交叉、变异等遗传操作具有随机性，可能破坏掉当前群体中适应度最好的个体，为此采用最优保存策略方法进行优胜劣汰操作。即按比例备份当代最优个体群，并与下次迭代产生的最优个体群作对比，二者择优保留。⑦根据经验，对于泵站机组优化调度遗传算法的主要控制参数设置如下：种群规模（M）100，遗传运算的终止进化代数（T）100，选择概率（Ps）0.08，交叉概率（Pc）0.4，变异概率（Pm）0.5。⑧收敛条件采用最大进化代数与收敛不等式相结合的方法，将收敛判别式设计为：

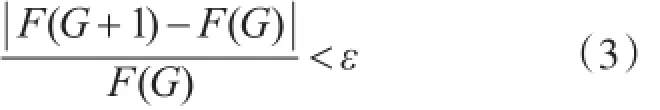
式中：F（G）为计算到第G代的泵站最小耗能；ε为0.001。

4 运算实例

4.1 泵站性能曲线拟合

根据实测效能数据，通过最小二乘法拟合得到泵站效能曲线的数学表达式。

流量-扬程拟合函数为：

效率-扬程拟合函数为：

式中：Q为流量（m3/s）；H为泵站扬程（m）；A0、A1、A2、A3为流量-扬程拟合系数；ƞ为效率；B0、B1、B2、B3为效率-扬程拟合系数。

首先拟合泵站在不同叶角下流量和效率关于扬程的效能曲线，再将这一组曲线方程储存在计算机内。在以后的寻优过程中，要多次调用上述曲线方程对离散工况点进行插值计算，以确定给定扬程下优选的流量和对应的效率及叶片角度。

4.2 目标函数建立

梯级泵站系统优化模型以梯级泵站系统总能耗最小为目标，以梯级泵站总功率为目标函数，建立关系，具体如下：

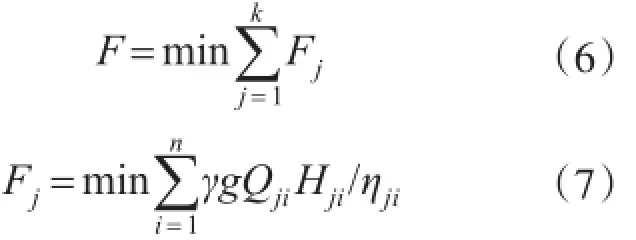
式中：F为梯级泵站总功率最小值（W）；Fj为第j级泵站的功率最小值（W）；Qji为第j级泵站的第i台机组的抽水量（m3）；Hji为第j级泵站的第i台机组的抽水扬程（m）；ηji为第j级泵站的第i台机组在扬程为Hji，抽水量为Qji下的装置效率；n为泵站的机组运行台数。

4.3 约束条件设定

梯级泵站系统中，各级泵站及泵站内各机组要同时满足一定的约束条件，具体如下：

（1）第j级泵站的水位约束为：

式中：hjmin和hjmax分别为第j级泵站与第j+1级泵站间输水渠道允许的最小和最大水位（m）。

（2）第j级泵站的流量约束为：

式中：Qj为第j级泵站的总抽水量（m3）；Qji为第j级泵站第i台机组的抽水量（m3）；Qjimin和Qjimax分别为第j级泵站第i台机组允许的最小和最大抽水量（m3）。

（3）第j级泵站各机组抽水功率约束为：

式中：Njimin和Njimax分别为第j级泵站第i台机组允许的最小和最大抽水功率（W）。

（4）机组运行台数约束为：

式中：nji为第j级泵站第i台机组运行台数；Numji为第j级泵站第i台机组最大允许运行台数。

（5）水泵叶片角度约束为：

式中：θji为第j级泵站第i台机组的叶片开启角度（°）；θjimin和θjimax分别为第j级泵站第i台机组的叶片最小、最大开启角度（°）。

4.4 梯级泵站优化结果

选取2011年两例工况，计算结果见表1。经计算可以看出，梯级泵站之间存在一定的最优运行水位，结合泵站站内优化，通过合理选择开机机组及机组运行叶角和流量分配，可以达到节能降耗的目标。

5 结论

根据引滦入津输水线路的实际水情和工情的特点，采用基于MIKE 11水动力模型模块，建立能够反映引滦输水线路河道水量、水位时空变化规律的数学模型。泵站优化调度模型在对泵站机组运行规律进行数据建模的基础上，采用遗传算法对泵站优化调度进行了分析研究，计算出满足工况的各级泵站最优机组组合和机组内部流量分配，并得出各机组运行叶角。经实例分析验证，该梯级泵站优化调度算法能起到明显节能降耗的作用。

表1 梯级泵站优化工况

[1]王小平，曹立明.遗传算法—理论、应用与软件实现[M].西安：西安交通大学出版社，2006.

[2]李敏强，寇纪淞，林丹，等.遗传算法的基本理论与应用[M].北京：科学出版社，2002.

[3]张文修，梁怡.遗传算法的数学基础[M].西安：西安交通大学出版社，2000.

Research of Optimized Dispatching of Cascade Pumping Stations Based on Hydrodynamic Dispersion Model and Genetic Algorithm

WU Hao1，ZHOU Zhi-hua1，GAO Ying2，LI Ji-ming2
（1.Tianjin Hydraulic Research Institute，Tianjin 300061，China；2.Administrative Department of Tianjin Luanhe River Diversion Project，Tianjin 301900，China）

Cascade pumping stations working together is the way of pumping water used in the Tianjin Luanhe River Diversion Project，aims at energy saving and consumption reducing，the method of optimizing water level and the running mode of pumping stations together are introduced in this paper after analyzing the working feature of the cascade pumping stations.The hydrodynamic dispersion model and optimized dispatching model of cascade pumping stations are built on the ground of DHI MIKE11 hydrodynamic dispersion model and genetic algorithm.Based on pumping stations operational log，the performance curve of the pumping stations is fit which help counting the energy used.The cascade pumping stations operational log in 2011 is used to validate this optimizing method and result shows that this method is rational and effective and can reach the goal of energy saving and consumption reducing.

optimized dispatching of cascade pumping stations；hydrodynamic dispersion model；genetic algorithm；performance curve

TV685

A

1004-7328（2014）04-0046-04

10.3969/j.issn.1004-7328.2014.04.017

2014-05-26

吴昊（1983-），女，硕士，工程师，主要从事防洪减灾、水利信息化方面的研究工作。