基于非均质边坡强度折减法的三维桥基边坡稳定性分析

胡松山，童申家，刘斌清，谭 华，覃润浦

（1.广西交通科学研究院 广西道路结构与材料重点实验室，南宁 530007；2.广西交通科学研究院 道路工程研究所，南宁 530007；3.西安建筑科技大学 土木工程学院，西安 710055）

1 引言

峡谷区高陡桥基岸坡工程是伴随西部大开发建设以来岩土工程界呈现出的又一复杂边坡问题。由于桥基边坡呈现出岩土体不连续性、非均质性及桥梁荷载作用下岩体变形机制的差异性等给桥基边坡的稳定性判断带来了诸多不便，影响桥梁的选型和工程造价，尤其桥梁下部结构带来的空间效应影响对实际工程提出了建立三维边坡稳定分析的要求，以便更加真实地反映桥基的实际工作状态。陈祖煜[1]提出用三维分析可以恰当地考虑滑体内由于滑裂面的空间变异特征对边坡稳定安全系数的影响。随着计算机技术的发展，有限元强度折减法的应用可以解决边坡几何形状不规则和材料不均匀性的问题。众多工程实践证明，运用三维有限元强度折减法计算工程边坡安全系数比较符合实际状况，同时可以得出边坡施工过程中岩土体的应力与应变情况，而且通过降低岩土参数模拟滑动面塑性区的发展过程，为边坡的开挖及加固方案的制定提供参考依据。总之，当前的理论分析大多关注于均质边坡安全系数的计算，均质边坡临界失稳状态的判断，屈服准则的使用，均质边坡滑动面位置的分布状况等，而对于非均质边坡的相关研究涉及较少，尤其针对非均质边坡的强度折减范围及其滑动面的位置的确定并未深入研究。

郭明伟等[2]在分析西南某桥基边坡的过程中，采用剪应力定义计算安全系数，同时也指出在工程实际中滑体的形状不规则，不同滑动方向得出的安全系数不同，如何确定潜在滑体的滑动方向是值得研究的问题。

在对边坡进行全部折减和局部折减的问题上，杨光华等[3]认为，边坡的失稳是由于局部土体的强度降低所致，并提出只对局部土体单元进行强度折减，其他土体单元保持原有强度不变的局部强度折减法，同时指出一般基于全单元强度折减法计算出来的变形场比局部强度折减法的要偏大。而薛雷等[4]则以FLAC3D为平台对一非均质二维边坡进行分析，认为局部强度折减在不能合理选择折减区域时不能够准确评价边坡的稳定性，并建议对整个边坡模型进行整体折减。由此可见他们持有矛盾的观点[3－4]。本文针对研究领域内存在的问题展开对非均质边坡强度折减范围、失稳判据研究，研究结论将应用于实际工程当中，为同类型边坡提供参考依据。

2 基于场变量的强度折减法

强度折减法分析边坡稳定性的技术关键是对计算结果的正确判断，进而分析坡体是否达到临界破坏状态，然而，对此多年来的研究者并未达到意见相一致。陈力华等[5]将此归结为强度折减法的正确使用，认为岩土体呈现张拉+剪破坏特征，而目前的强度折减法仅对坡体的抗剪强度参数(c,tan φ)进行折减，忽略了抗拉强度参数T 的影响。

为了更加快速准确地求出边坡的安全系数，本文借助于在大型通用有限元软件ABAQUS，在软件中设置场变量，建立场变量与增量步时间和材料参数的函数关系，实现折减岩体抗剪强度参数和抗拉强度参数随增量步时间变化，通过对软件中时间步设置，实现材料参数的自动折减，使得整个桥基边坡模型在软件中自动完成全部折减过程，快速求得安全系数及塑形变形场。具体实施用公式为

式中：cini、φini、Tini分别为材料的初始黏聚力、内摩擦角和抗拉强度；c、φ、T 分别为随场变量变化的材料的黏聚力、内摩擦角和抗拉强度；t为增量步时间，0≤t≤1；a、b为可调参数，且均大于0，满足：＞1，b≠0 。

3 强度折减范围

为了便于进一步探讨强度折减范围对边坡安全系数产生的影响，参照薛雷等[4]提出的“黏聚力比”概念对一般边坡和高陡边坡2个典型算例进行研究。黏聚力比是指在分析模型当中边坡底部一层岩土的黏聚力与上部岩土层黏聚力之比，公式为

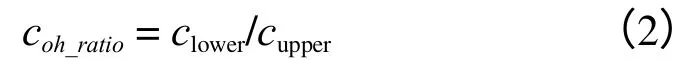
式中：clower、cupper分别为下部与上部岩土层的黏聚力。

（1）计算模型1

一般边坡三维计算模型如图1 所示，该边坡的二维效果图见文献[5]所采用的算例边坡。土体为服从Mohr-Coulomb 模型与非关联流动法则的理想弹塑性材料。为便于研究，假设该边坡由上下2 层土组成的非均质边坡，计算区域长105 m，高40 m，厚度方向取为50 m。整体模型的边界条件：除坡面外所有的边界垂直面和底面全部进行法向约束。材料参数见表1，其中上层土黏聚力值固定不变，下层土黏聚力值按式（2）计算。

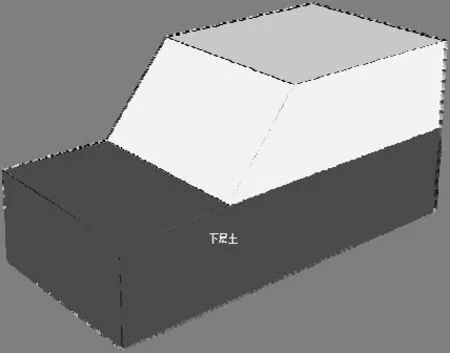
图1 非均质一般边坡三维分析模型（算例1）Fig.1 Three-dimensional slope model of the inhomogeneous general slope(example 1)

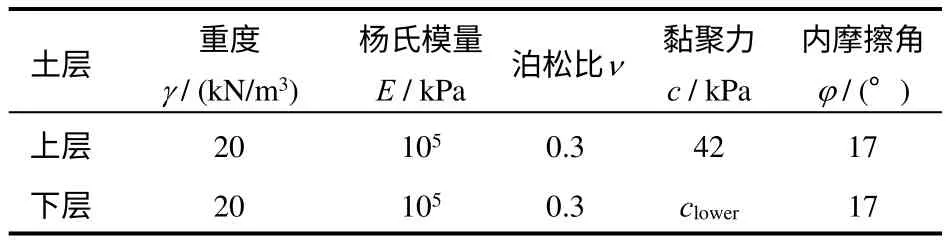
表1 材料参数Table 1 Material parameters

由于一般边坡计算模型涉及两种材料，为便于研究非均质边坡各土层不同黏聚力比下局部强度折减法与整体强度折减法的区别，分别取不同黏聚力比给底层土黏聚力Clower赋值，其余参数不变(见表1)，并计算相应的安全系数，如图2 所示。

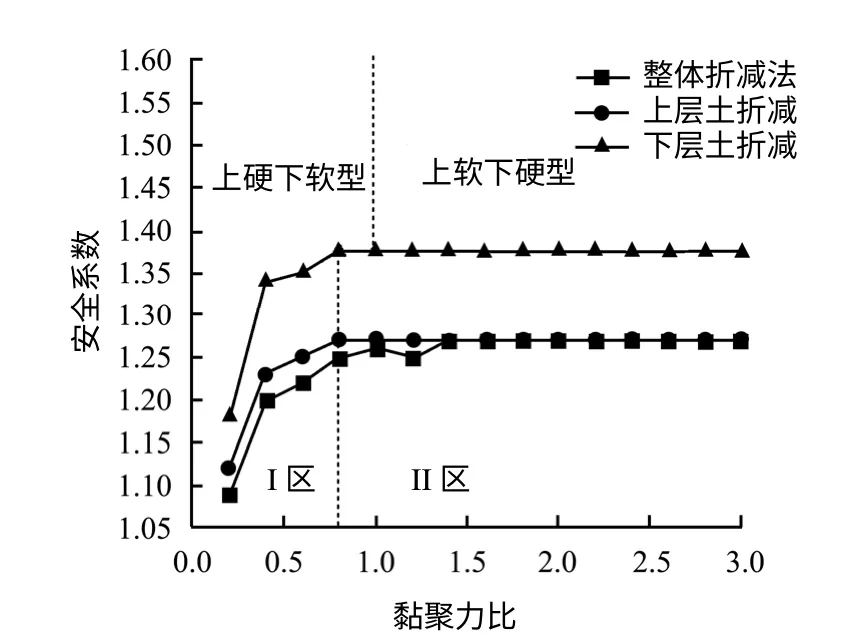
图2 不同黏聚力比下整体与局部强度折减安全系数对比图（算例1）Fig.2 Computed FOS for different cohesive ratios based on global and local strength reduction(example 1)

分析图2 发现，黏聚力比c=1 时一般边坡可概化为上硬下软型和上软下硬型两种，c=0.8 时将安全系数与黏聚力比曲线分为I 区和II 区。I 区域，即黏聚力相差不大情况下仅对下层土折减计算出来的安全系数要大于整体折减和上部折减，若对局部软弱层折减强化了实际边坡的安全储备能力；II 区域，边坡下层较硬时，整体折减与仅对上层土折减结果基本一致。可见在一般边坡中只有当黏聚力相差不大的情况下对黏聚力较小土层实施局部折减，才能得到合理的安全系数，而对于坡体内存在岩质相差较大的边坡建议采用整体强度折减。

为便于对比一般边坡整体折减与局部折减的滑动面位置，将计算得出的三维塑性区云图见图3，再现边坡体中变形发展过程，且可以清晰辨出整体强度折减与局部强度折减的异同。

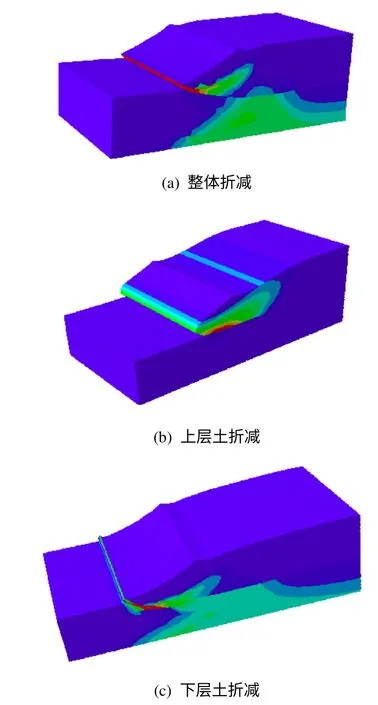
图3 黏聚力比0.8 的整体与局部折减塑性区云图（算例1）Fig.3 Plastic zone contours of cohesive ratios 0.8 based on global and local strength reductions(example 1)

（2）计算模型2

陡边坡三维计算模型见图4，该边坡的二维效果图亦参考文献[5]所采算例。边坡材料为服从Mohr-Coulomb 与非关联流动法则的理想弹塑性材料。为便于研究，假设该边坡由上下2 层土组成的非均质边坡，计算区域长220 m，高170 m，厚度方向取为50 m。整体模型的边界条件为：除坡面外所有的边界垂直面和底面全部进行法向约束。材料参数见表2，其中上层土黏聚力值固定不变，下层土黏聚力值按式（1）计算。

为了研究陡边坡各土层不同黏聚力比下局部强度折减法与整体强度折减法的异同，运用本文提出的引入场变量的强度折减法分别对整体强度折减、仅对上层土局部折减、仅对下层土局部折减，将计算得出的边坡安全系数进行对比分析，如图5 所示。

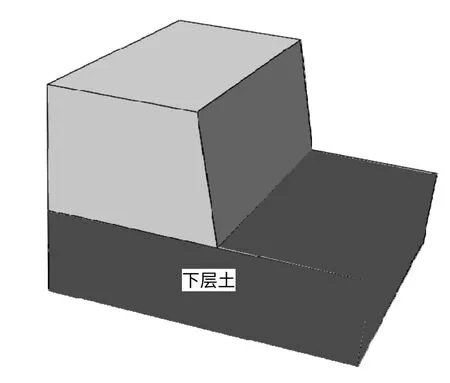
图4 非均质陡边坡三维分析模型（算例2）Fig.4 Three-dimensional slope model of the inhomogeneous steep slope(example 2)

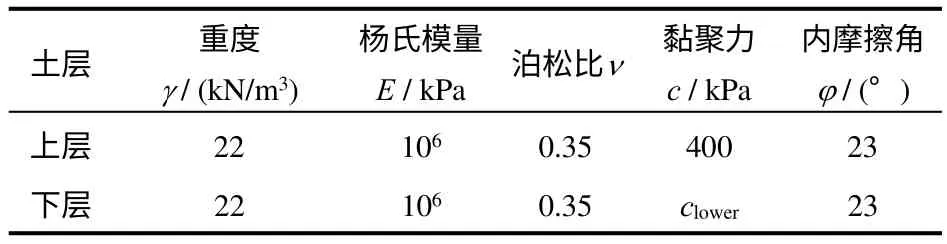
表2 材料参数Table 2 Material parameters

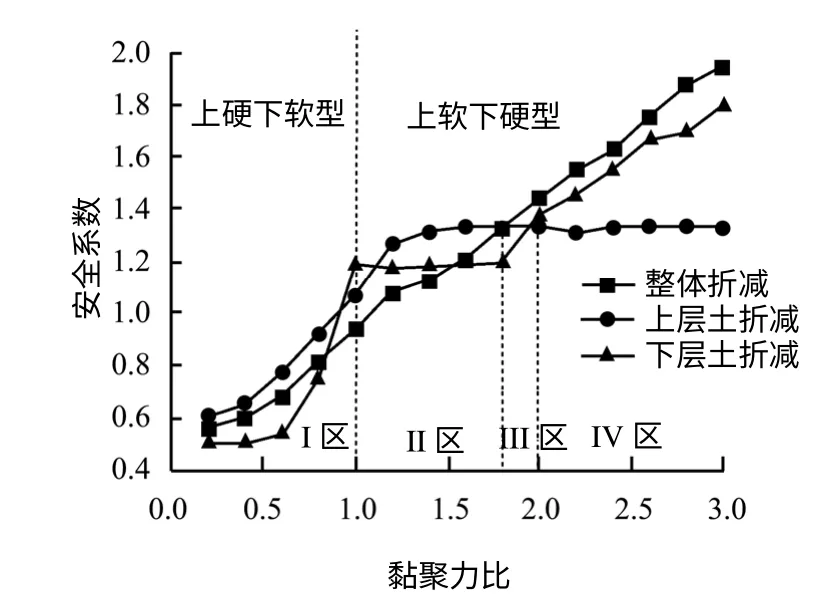
图5 不同黏聚力比下整体与局部强度折减安全系数对比图（算例2）Fig.5 Computed FOS for different cohesive ratios based on global and local strength reduction(example 2)

对于陡边坡，其安全系数与黏聚力变化曲线呈现出与一般边坡不同的趋势，分析图5 特征为：（1）由图5(a)可见，随着土层结构黏聚力比的增加，相应的坡体安全系数在增加，这一结果与实际当中的诸多工程案例不相符。由于边坡存在软弱岩体，尤其是高陡岩质边坡存在软弱结构面，坡体不能呈现较好的安全储备能力。此时对整个边坡进行强度折减并未得出较好的结论。（2）由图5(b)可见，位于I 区时，边坡模型属于上硬下软型，即坡体下部存在软弱岩土结构，此时随着黏聚力比的增加，对下层土进行局部折减得出的安全系数逐步增加，在合适的条件下超过整体折减结果。在II 区，下部土层强度逐渐接近甚至超过上部土层强度，数值模型逐步转化为上软下硬型，此时在黏聚力比为1.0～1.8时，对下部相对硬土层折减计算的安全系数几乎不变，而当黏聚力比达到1.8 以上，即位于III和IV时，整体趋势接近于整体折减曲线。（3）由图5(c)可见，位于II 区时，折减结果大于整体折减，且在黏聚力比值达到1.2 时，出现边坡安全储备临界状态，即随着下部土层硬度的增大，对坡体上部相对软弱岩层进行局部折减的结果不变。结合实际工程可以解释为，当边坡上部出现局部软弱结构层时，软弱结构层的稳定性决定了整个边坡的安全与否，对相对较弱的岩体折减可以得出与实际相符合的结果。

对比分析3 种变化曲线得出，对于高陡三维边坡而言，对相对较软的岩体进行局部折减可以得出较为可信的结果，而整体折减不仅给计算来带较多的分析时间，而且得出的结果在某种程度上与实际相违背。

图6为陡边坡部分不同黏聚力比下整体与局部强度折减计算所得塑性区云图。

图6 不同黏聚力比下整体与局部折减塑性区云图（算例2）Fig.6 Plastic zone contours of different cohesive ratios based on global and local strength reductions(example 2)

由图6 可见，边坡潜在的危险滑动面所在位置、滑动面状态及分辨出整体强度折减与各局部强度折减法的异同。对比发现，折减区域不同，相应的边坡塑性区也不一样，整体折减和只对上层土体折减，塑性区分布于上层土；而只对下层土折减，塑性区出现于下层土。可见，折减局部土体强度获得的变形更接近真实变形，即对高陡边坡进行局部强度折减更为合理。

4 关于非均质边坡失稳判据的探讨

目前研究领域对边坡濒临破坏的极限状态的判断采用3 种依据，即计算不收敛、塑性区贯通和特征点位移法。然而许多专家学者对此3 种判断依据看法不一。收敛性判断要求有一个保证大型高陡边坡计算能够完全收敛的有限元软件，而目前没有此类软件。刘金龙等[6]认为，有限元数值计算收敛时也不一定表明边坡处于安全状态。赵尚毅等[7]指出，塑性区贯通是边坡破坏的必要非充分条件。传统的特征点位移法虽说概念简单、较易接受，但在实际操作中误差较大，并且常常遇到特征点不明显或出现多个特征点现象，混淆判断依据。

基于上述分析及上文计算过程中遇到的现象，本文采用坡体内关键部位特征点位移（水平位移或竖直位移）随折减系数的变化率，即特征点位移增量Δδ 与强度折减系数增量ΔFt比值ΔδΔFt和强度折减系数 Ft的关系曲线的突变点来确定边坡的临界失稳状态。

5 工程实例

石门大桥位于新疆省呼图壁河中上游的石门水电站库区上游，桥基岸坡为典型的“U”型沟谷，地形起伏较大，两岸陡峻，岸坡高约60 m，坡度为50°～90°，坡脚堆积少量的崩塌巨石，出露地层为卵石、泥岩、砂岩[8]。桥址区地表发育有较密的低矮植被，河道内常年流水。桥位河床海拔1 176 m，古河道河床海拔1 152 m，枯水期水位高程为1 185 m，正常蓄水位为1 240 m，沟谷底部宽约50 m，沟谷顶部宽约175 m。左岸边坡呈现上缓下陡形式，上部陡度为12°，下部陡度为48°，右岸边坡坡度为53°。U 形谷中阶地不发育，仅零星分布于U 形谷下部，一般为侵蚀阶地或基座阶地，新构造活动期，本区地壳处于间歇性抬升状态，河谷地貌大致经历宽谷期和峡谷期。桥型选择为上部结构90 m+150 m+90 m连续刚构，加6 m×25 m 预应力混凝土现浇连续箱梁。大部分桥墩分布于左岸桥基，本文拟对左岸对桥梁主墩影响较大的高陡边坡为工程实例，采用本文提出的分析方法对其进行稳定性分析。

5.1 三维桥基边坡体计算模型

根据场地工程地质勘察，桥位地层分布受构造控制，主要出露侏罗系和第四系，岩性为砂岩、泥岩、粉砂岩、粉土层、冲洪积（Q3al+pl）卵、砾石层，冲洪积（Q4al）卵、砾石层。第四系松散沉积物广泛分布于沟谷、岸坡较缓及桥址上下游大型不良地质体分布区。两岸边坡在漫长的地质历史中，历经燕山构造运动与喜马拉雅运动，受陡峭两岸的卸荷作用，使两岸的砂岩中发育以顺河向为的大量卸荷裂隙，造成河道左岸（大桥K80+552 主墩旁）一处危岩体见图7、8。

图7 危岩照片（拍摄方向为南-北）Fig.7 Crag photo(shooting direction:south to north)

图8 左岸风化凹槽（拍摄方向为北-南）Fig.8 The weathering groove of the left bank(shooting direction:north to south)

根据现场勘测，左岸桥坡表层卵石厚约24 m，卵石层以下为砂岩、泥岩，上部基岩裸露陡立，表层为强风化～中等风化状态。下部基岩缓倾，表层为全风化～强风化状态。根据现场工程地质情况和主要的地层分布，建立三维有限元分析模型，三维模型的几何尺寸为：沿桥轴线方向取包括桥墩在内的范围380 m；沿垂直于桥轴线方向，取桥轴线上下游400 m 的范围；沿河床向下取100 m 范围作为研究对象。其中岩层划分见图9，有限元模型见图10。计算模型中包括岩体材料分布、软弱结构面及墩台。计算边界条件：除坡面外所有的边界垂直面和底面全部进行法向约束。为了便于看出桥基岸坡岩层划分结构，根据现场勘测报告对主桥墩K80+642 位置地层岩性从上到下为4.0 m 粉土，8.5 m卵石，2.0 m 中分化泥岩，4.5 m 微风化泥岩，3.0中风化砂岩，2.0 m 强风化砂岩，15.2 m 中风化砂岩，3.3 m 中风化泥岩，7.0 m 中风化砂岩，2.5 m中风化泥岩和8.0 微风化砂岩。具体工程地质纵断面图见文献[8]。

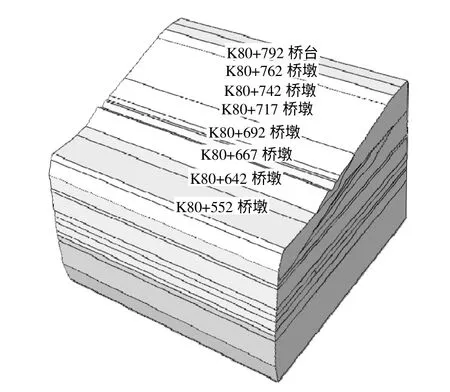
图9 左岸桥基边坡岩层结构划分Fig.9 The left bank abutment slope rock structure

图10 三维有限元分析模型Fig.10 3D finite element analysis model

5.2 计算模型参数选取

根据工程区域岩土体的室内试验，通过查阅岩石参数手册[9-12]，并参考类似工程所有的力学参数，三维边坡模拟计算时天然状况下和饱水条件下的岩体及软弱结构面强度参数见表3、4。鉴于岩体力学中，Druck-Prager 屈服准则比Mohr-Coulomb 屈服准则更能准确描述岩石强度的强度准则，在对边坡进行弹塑性有限元分析时，岩体采用Druck-Prager 准则，结构面采用Mohr-Coulomb 准则。

为清楚显示各个阶段安全系数Fs的确定所对应结构面的强度值，建立软弱结构面强度参数随场变量变化曲线图，如图11、12 所示。

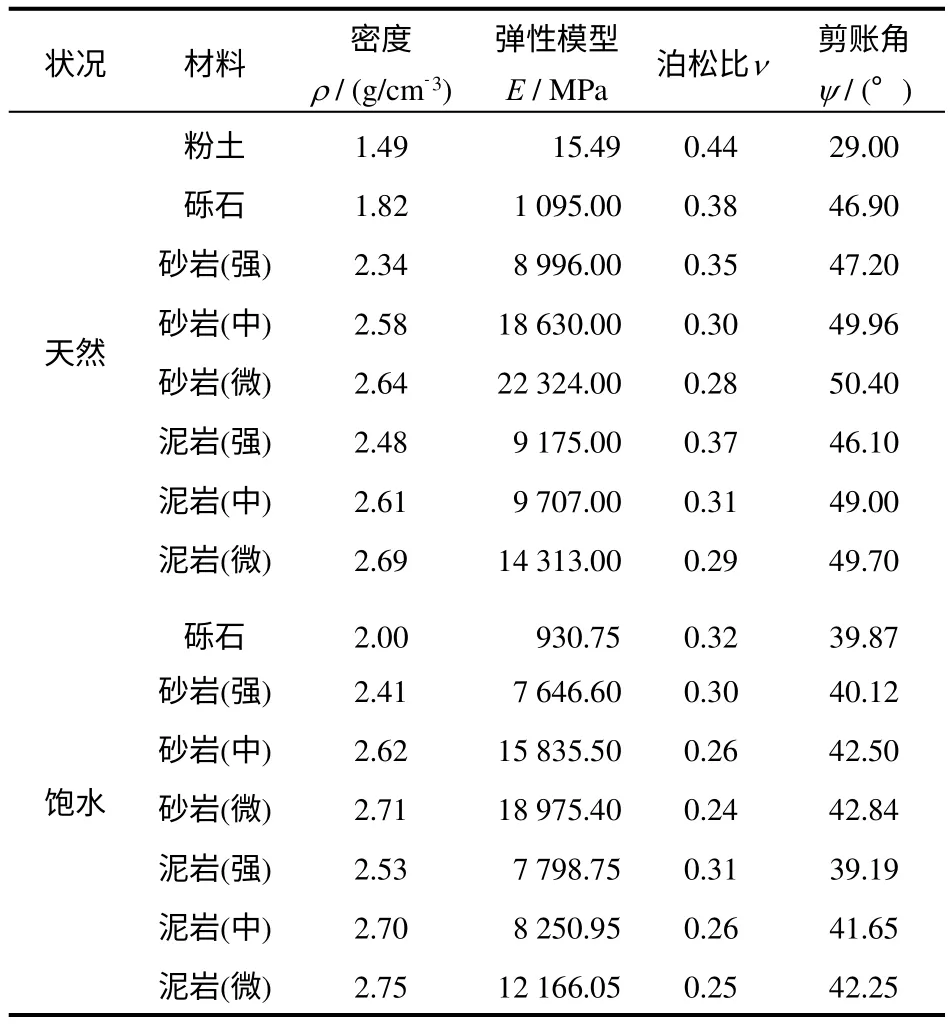
表3 基于Drucker-Prager 模型物理力学参数（天然条件下）Table 3 Physical and mechanical parameters of Drucker-Prager model(based on the natural conditions)

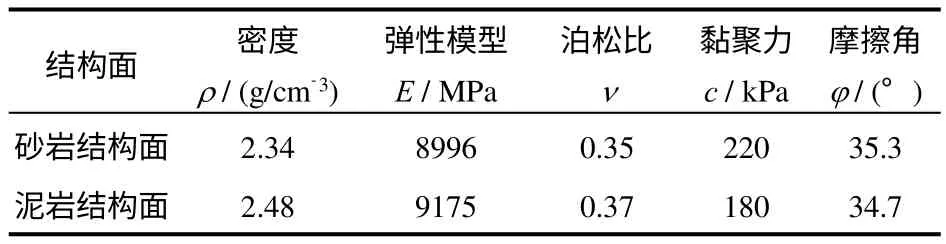
表4 基于Mohr-Coulomb 模型的软弱结构面力学参数Table 4 Weak structure mechanical parameters based on Mohr-Coulomb model

5.3 三维桥基稳定性分析

石门大桥左岸桥基岸坡属于典型的高陡岩质边坡，结合本文研究结论对岸坡相对软弱结构岩体及软弱结构面进行强度折减，在折减过程中并考虑材料抗拉强度指标的影响，避免了分析过程中不合理塑性区的出现。图13为坡体处于极限状态下的等效塑形应变图，图14为沿桥轴线方向坡体内部剖面的塑形变形图。显见，坡面卵石层表面的粉土层已有塑性流动区域。进一步结合最大主应力等值线云图可见，最大主应力分布于后坡面桥台位置、卵石层以下的强风化砂岩层等处，根据现场岩层钻孔柱状图资料显示，此部位岩体完整性评价为破碎状态，所形成的集中拉应力区域尤其会导致后坡面桥台两侧岩石出现局部拉破坏。

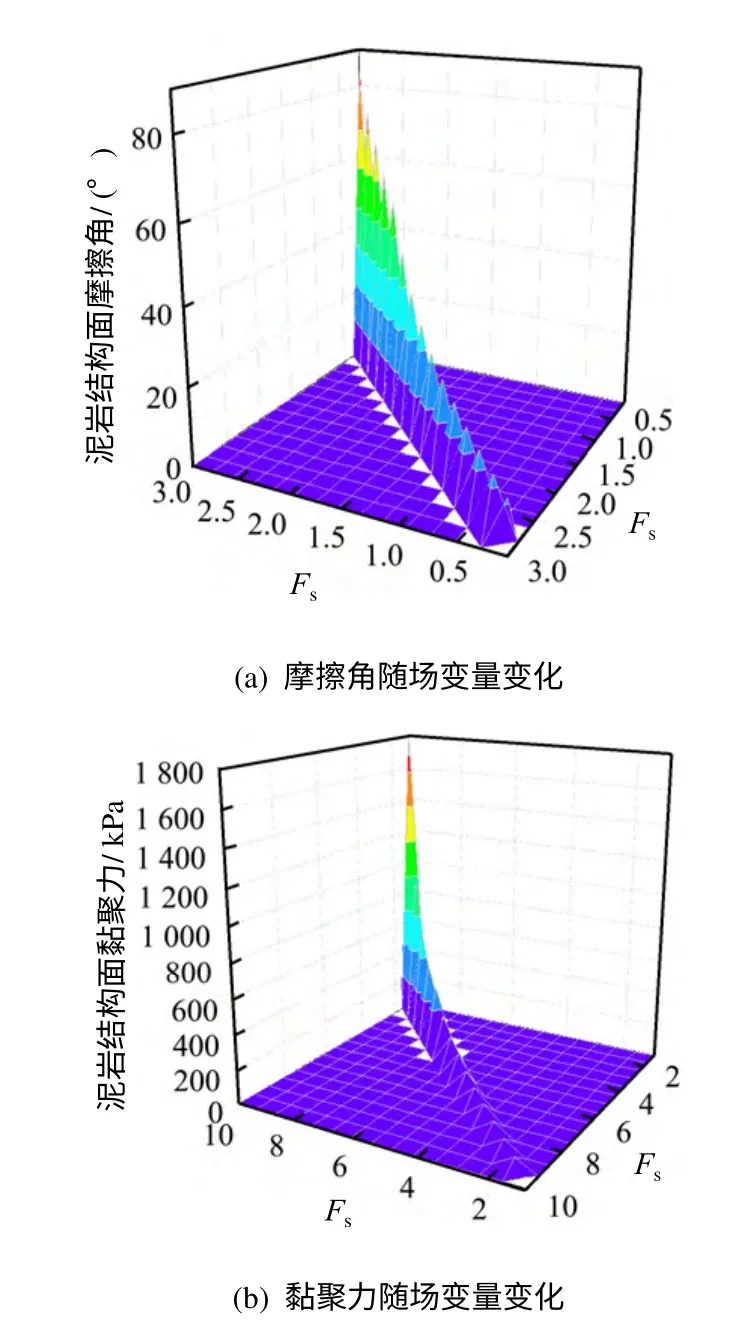
图11 泥岩结构面摩擦角和黏聚力随场变量变化三维曲面图Fig.11 Mudstone structure surface friction and cohesion with field variables change 3-D surface chart

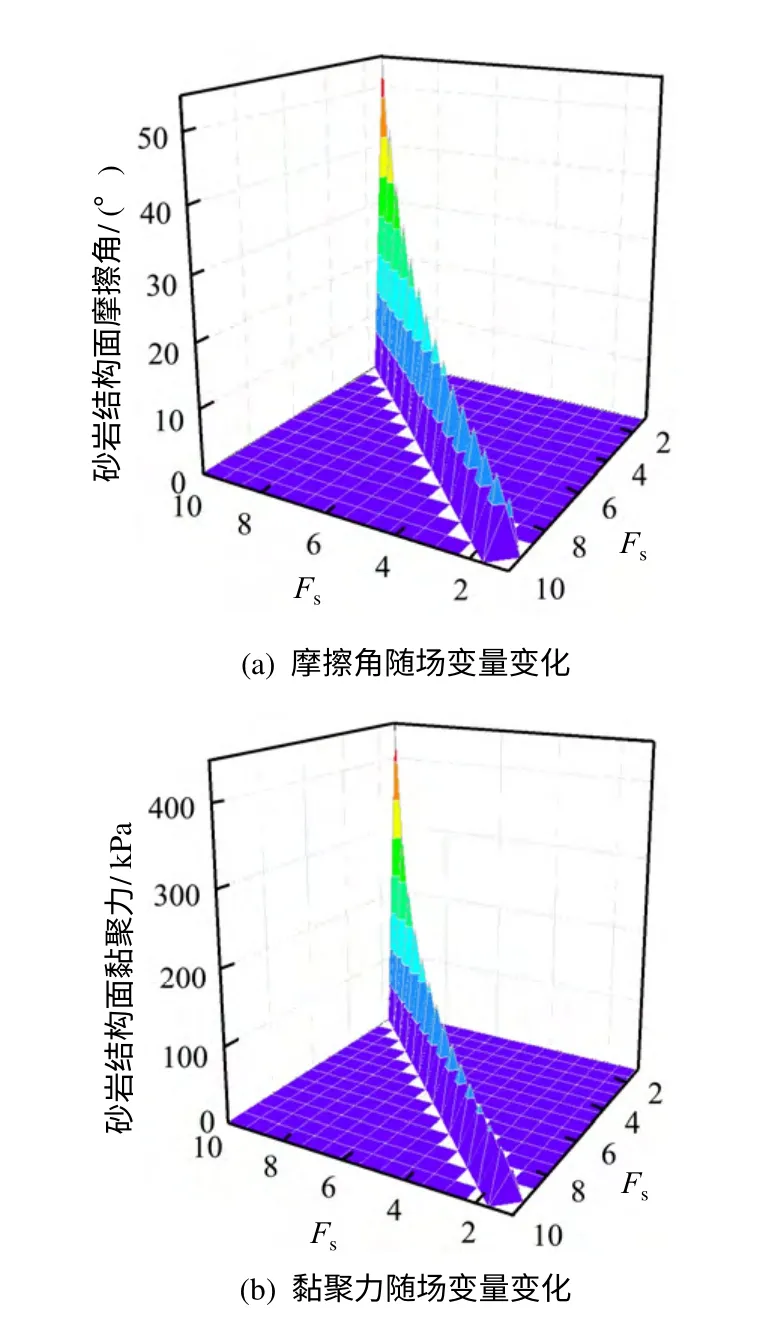
图12 砂岩结构面摩擦角和黏聚力随场变量变化三维曲面图Fig.12 Sandstone structure surface friction and cohesion with field variables change 3-D surface chart

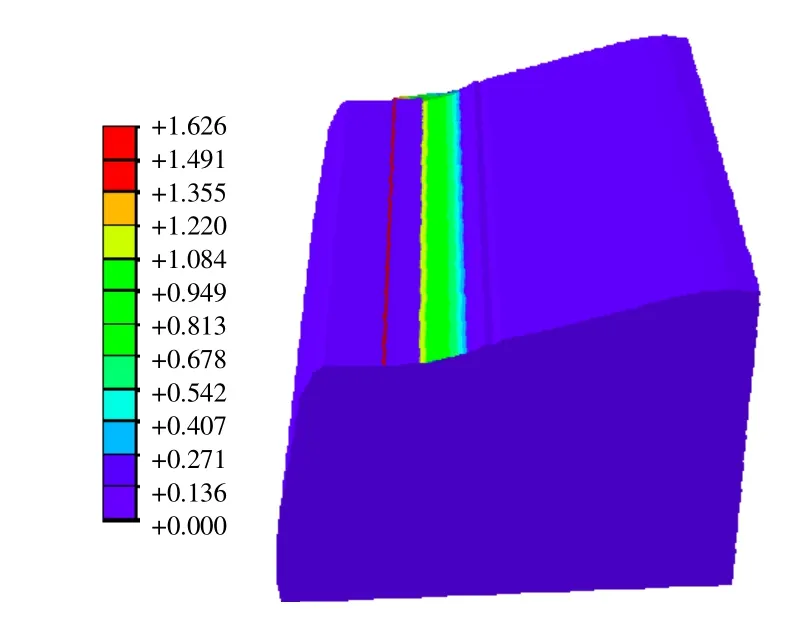
图13 天然状态下桥基坡体的塑形变形图Fig.13 Plastic deformation of bridge foundation slope shape in natural state

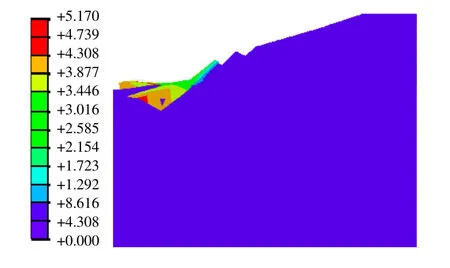
图14 极限状态下沿桥轴线方向坡体内部剖面的塑形变形图（局部放大图）Fig.14 Plastic deformation of section along bridge axis at ultimate state(partial enlarged drawing)

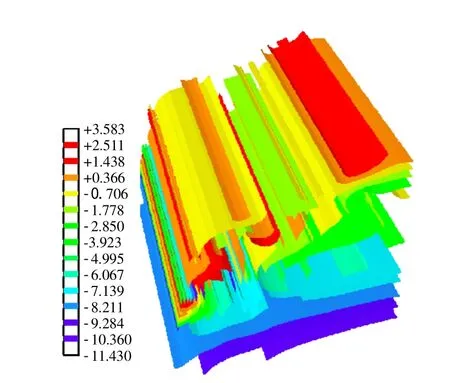
图15 最大主应力等值线云图（单位：102 kPa）Fig.15 Maximum principal stress nephogram(unit:102 kPa)

为了分析传统特征点位移法给人为判断边坡安全系数带来的不变，观察图16 显见，随着场变量的增加，竖向位移同步增大，曲线在场变量为1.2和1.6 两处出现位移突变点，混淆正确判断边坡的稳定性。考虑到工程设计单位所关心的大桥桥基在各种工况下的变形问题，并满足桥基横向无变形且允许竖直方向有10 mm 变形的桥梁设计要求。故，桥梁墩台的变形量是研究的重点，并结合本文提出的失稳判别依据，以K80+552 桥墩、K80+642 桥墩、K80+667 桥墩、K80+692 桥墩、K80+717 桥墩、K80+742 桥墩、K80+767 桥墩、K80+792 桥台等作为边坡稳定关键部位特征点，并给出其ΔδΔFt-Ft关系曲线，如图17 所示。

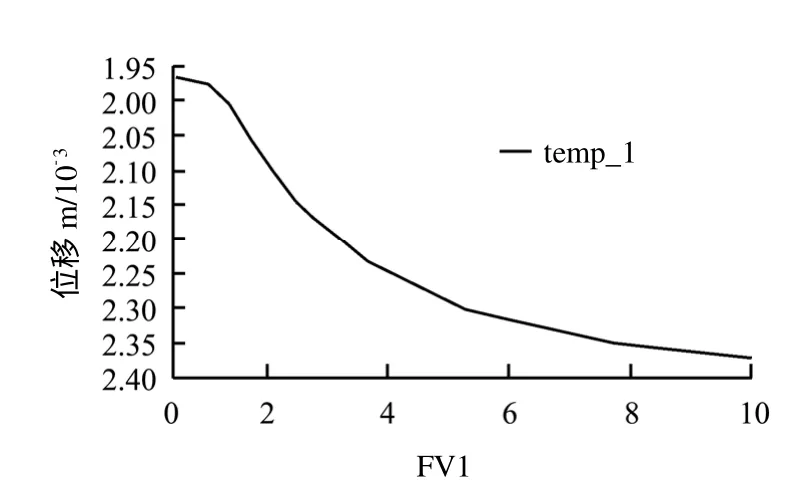
图16 场变量FV1 随水平位移变化曲线Fig.16 Relationship curve between horizontal displacement and field variation FV1

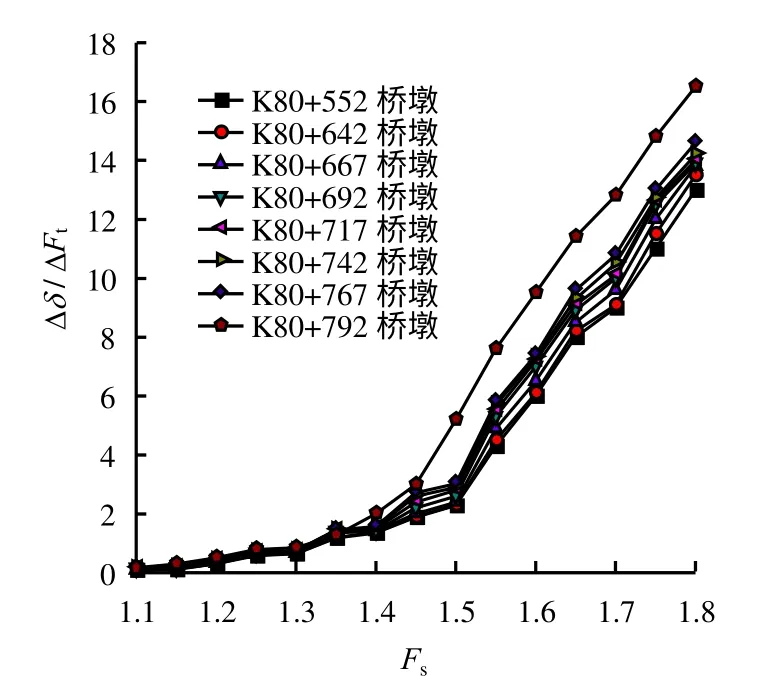
图17 关键点ΔδΔF t-Ft 关系曲线Fig.17 Relationshipcurves betweenΔδΔFt andFt

由图17 可见，当折减系数增加到1.50 时，关键部位K80+552 桥墩～K80+767 桥墩的ΔδΔFt值突然急剧增加，由此判断整体桥基边坡安全系数为1.50，特别指出关键点K80+792 桥台出局部安全系数为1.45，这与该处出现最大主应力集中区相符，说明该处岩体相对其他部位安全储备能力较低。总之，文中采用的位移随折减系数变化速率判据所显示的位移突变点较为明显，进而体现出判据的准确性和较强的实用性。

现场勘察发现，岸坡顶部卵石层属于水库蓄水后的水位变动区，岸坡在后期水库水浸泡及水流掏蚀，有滑塌趋势。因此，为避免桥梁运营期间该部位卵石滑塌所产生的涌浪给大桥构筑物造成破坏性影响，工程要求对左岸桥基岸坡表层做削坡处理，边坡坡率为1:2。考虑到所建大桥大部分桥墩位于左岸边坡，加上后期蓄水影响，有必要计算桥梁运营期间边坡安全系数大小，计算结果如图18 所示。计算发现，削坡后的桥基在桥梁荷载及水库蓄水条件下，边坡安全系数明显下降。总体边坡安全系数为1.13。根据《公路路基设计规范》[18]第7.17.3 条第4 款规定：路堤和库岸稳定安全系数不应小于1.25，当考虑水位升降变化作用影响时，稳定安全系数不应小于1.05～1.15。很显然，此时岸坡处于临界稳定状态，为保证整体岸坡有足够的安全储备性能[14]，建议在对边坡削坡处理后，尚应对其进行锚固处理。建议锚固范围为上下游各50 m，枯水位以下5 m 至厚层砂岩层以上5 m（即海拔高程1 180～1 230 m），水平向锚固深度大于30 m。

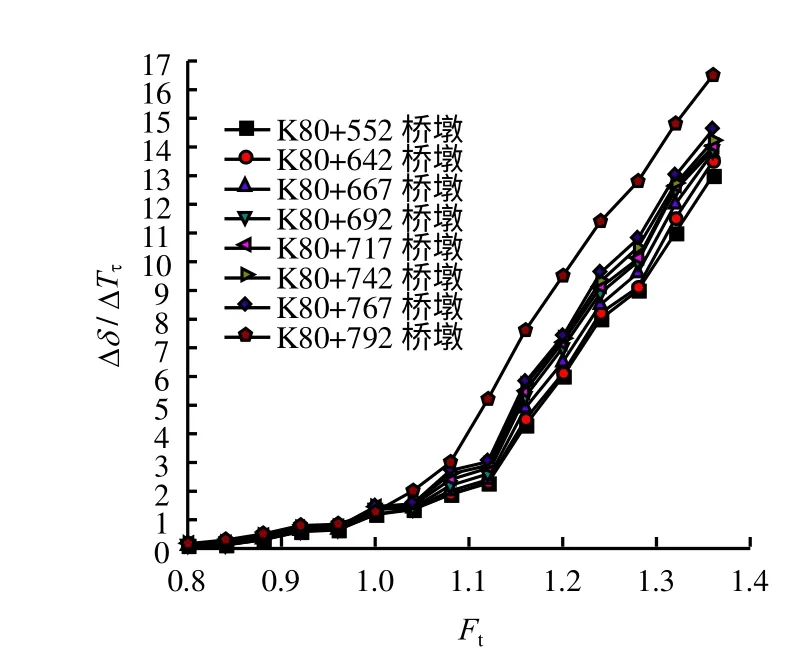
图18 工况：蓄水+桥梁荷载作用时关键点Fig.18 Relatio nships betweenΔδΔFtandFtΔδΔFt-Ft关系曲线in waterstorageadd bridgeload

6 结语

在对非均质边坡研究中给出了一般边坡和高陡边坡折减范围的理论依据。本文分析方法建立在三维有限元分析[16]中，比以往学者分析方法更接近工程实际，在高陡边坡中建议对相对较弱岩体进行局部折减。

采用基于场变量的强度折减法[13,15,17]，并同时考虑抗剪强度参数和抗拉强度参数的影响，在计算结果的准确性及计算效率上比传统方法均有大幅度的提高，结果表明该方法求边坡安全系数是有效的，具有一定的可行性。

针对传统边坡失稳判据的不足，提出对特征点位移法中关键拐点选择的改进，并将其应用于实际工程中，结果显示该方法可弥补传统方法中的不足。另外，该方法的应用较准确地预测出石门大桥后期运营中存在的隐患，对工程边坡的治理提供较为可靠的理论依据。

[1]陈祖煜.土质边坡稳定性分析—原理·方法·程序[M].北京:中国水利水电出版社,2003:533－535.

[2]郭明伟,李春光,王水林.基于有限元应力的三维边坡稳定性分析[J].岩石力学与工程学报,2012,51(12):2494－2500.GUO Ming-wei,LI Chun-guang，WANG Shui-lin.Threedimensional slope stability analysis based on finite element stress[J].Chinese Journal of Rock Mechanics and Engineering,2012,51(12):2494－2500.

[3]杨光华,钟志辉,张玉成,等.用局部强度折减法进行边坡稳定性分析[J].岩土力学,2010,31(增刊2):53－57.YANG Guang-hua,ZHONG Zhi-hui,ZHANG Yu-cheng,et al.Slope stability analysis by local strength reduction method[J].Rock and Soil Mechanics,2010,31(Supp.2):53－57.

[4]薛雷,孙强,秦四清,等.非均质边坡强度折减法折减范围研究[J].岩土工程学报,2011,33(2):275－280.XUE Lei，SUN Qiang,QIN Siqing,et al.Scope of strength reduction for inhomogeneous slopes[J].Chinese Journal of Geotechnical Engineering,2011,33(2):275－280.

[5]陈力华,靳晓光.有限元强度折减法中边坡三种失效判据的适用性研究[J].土木工程学报,2012,45(9):136－146.CHEN Li-hua,JIN Xiao-guang.Study on the applicability of three criteria for slope instability using finite element strength reduction method[J].China Civil Engineering Journal,2012,45(9):136－146.

[6]刘金龙,栾茂田,赵少飞,等.关于强度折减法有限元方法中边坡失稳判据的讨论[J].岩土力学,2005,26(8):1345－1348.LIU Jin-long,LUAN Mao-tian,ZHAO Shao-fei,et al.Discussi-on on criteria for evaluating stability of slope in elasto-plastic FEM based on shear strength reduction technique[J].Rock and Soil Mechanics,2005,26(8):1345－1348.

[7]赵尚毅,郑颖人,张玉芳.极限分析有限元法讲座—II.有限元强度折减法中边坡失稳的判据探讨[J].岩土力学,2005,26(2):332－336.ZHAO Shang-yi,ZHENG Ying-ren,ZHANG Yu-fang.Study on slope failure criterion in strength reduction finite element method[J].Rock and Soil Mechanics,2005,26(2):332－336.

[8]童申家,胡松山,闫仙丽.基于CSMR与模糊集理论的石门大桥桥基边坡稳定性评价[J].土木工程学报,2013,46(9):1－7 TONG Shen-jia,HU Song-shan,YAN Xian-li.Shimen bridge foundation slope stability assessment based on fuzzy set and CSMR[J].China Civil Engineering Journal,2013,46(9):1－7.

[9]CHEN Z,MORGENSTERN N R.Extensions to the generalized method of slices for stability analysis[J].Canadian Geotechnical Journal,1983,20(4):104－109.

[10]MANZARI M T,NOUR M A.Signification of soil dilatancy in slope stability analysis[J].Journal of Geotechnical and Geoenvironmental Engineering,2000,126(1):75－80.

[11]STIANSON J R,FREDLUND D G,CHAND.Three-dimesional slope stability based on stresses from astress-deform ationanalysis[J].Canadian Geotechnical Journal,2011,48(6):891－904.

[12]水利水电科学研究院，水利水电规划设计总院，水利电力情报研究所.岩石力学参数手册[M].北京：水利电力出版社，1991:409－511.

[13]李宁,许建聪.基于场变量的边坡稳定分析有限元强度折减法[J].岩土力学,2012,33(1):314－318.LI Ning,XU Jiancong.Strength reduction FEM for slope stability analysisbas-ed on field variable[J].Rock and Soil Mechanics,2012,33(1):314－318.

[14]漆祖芳,姜清辉,唐志丹,等.锦屏一级水电站左岸坝肩边坡施工期稳定分析[J].岩土力学,2012,33(2):531－538.QI Zu-fang,JIANG Qing-hui,TANG Zhi-dan,et al.Stability analysis of abutment slope at left bank of Jinping-I Hydropower Project during construction[J].Rock and Soil Mechanics,2012,33(2):531－538.

[15]邓华锋,李建林,王乐华,等.基于强度折减法的库岸滑坡三维有限元分析[J].岩石力学,2010,31(5):1604－1608.DENG Hua-feng,LI Jian-lin,WANG Le-hua,et al.3D finite element analysis of reservoir bank landslide based on strength reduction method[J].Rock and Soil Mechanics,2010,31(5):1604－1608.

[16]林杭,曹平,李江腾,等.基于Hoek-Brown 准则的三维边坡变形稳定性分析[J].岩土力学,2010,31(11):3656－3660.LIN Hang,CAO Ping,LI Jiang-teng,et al.Deformation stability of three-dimensional slope based on Hoek-Brown criterion[J].Rock and Soil Mechanics,2010,31(11):3656－3660.

[17]杨光华,张玉成,张有祥.变模量弹塑性强度折减法及其在边坡稳定分析中的应用[J].岩石力学与工程学报,2009,28(7):1506－1512.YANG Guang-hua,ZHANG Yu-cheng,ZHANG You-xiang.Variable modulus elastoplastic strength reduction method and its application to slope stability analysis[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(7):1506－1512.

[18]中交第二公路勘察设计院有限公司.JTG D30－2004公路路基设计规范[S].北京:人民交通出版社,2004.