非贯通随机节理岩体的结构效应对地下洞室地震响应的影响

崔 臻，冷先伦，朱泽奇，盛 谦

（1.中国电建集团 华东勘测设计研究院有限公司，杭州 310014；2.浙江中科依泰斯卡岩石工程研发有限公司，杭州 310014；3.天津大学 建筑工程学院，天津 300072；4.中国科学院武汉岩土力学研究所岩土力学与工程国家重点实验室，武汉 430071）

1 引言

随着西部大开发战略的实施，一大批大型水利水电工程已经或即将在我国西部营建，这些大型水利水电工程多数都设计有大型或超大型地下洞室群作为主要的水工建筑物。对于修建在复杂地质条件下的地下洞室，由于洞室开挖涉及到特殊的地层及岩体结构条件，一般围岩变形与破坏主要受围岩性状以及围岩中节理裂隙等结构的切割所控制。这种控制效应可以统一概括为节理岩体的力学参数效应和节理岩体的结构效应，其中，结构效应是指岩体中结构面的空间分布、组合规律等几何特征对岩体工程的影响[1]。

由于西部地区又是强地震多发地区和高抗震设防地震烈度地区，这些地下洞室又将直接面临地震稳定性问题。节理岩体的结构效应将对地下洞室的地震响应产生什么影响，是一个亟待解决的工程问题。

对于该问题目前常采用数值模拟方法来求解，常规的数值分析方法在建立数值模型时往往难以反映真实的岩体节理裂隙，多将岩体概化为等效连续体，采用连续介质力学的方法进行求解[2－4]，或者将原本断续的节理裂隙简化为完全连通的不连续面，将岩体切割为相互独立的离散块体，采用不连续方法进行求解[5－6]。

随着计算方法及计算机硬件条件的发展，使得对岩体节理裂隙不进行简化而直接进行求解变为可能。节理网络有限元[7]（jointed finite element method,简称JFEM）是指具有节理网络模拟功能的有限元，其中岩石材料采用实体单元模拟，岩体结构采用节理单元模拟。节理网络有限元方法以现场地质调查所获得的节理裂隙展布为基础，以随机节理网络模拟技术为指导，建立非贯通的随机节理网络地质模型，在此基础上，将节理网络和界面单元相结合形成节理岩体力学模型进行求解计算。传统的工作主要集中在节理岩体渗流模型和宏观力学参数与REV 尺度的研究上[8]，而直接应用于对工程静/动力稳定性的研究目前并不普遍。

为研究非连通随机节理岩体的结构效应对地下洞室地震响应的影响，本文探讨了节理网络的生成原理，给出了结构效应影响的表征参数，以大岗山水电站主厂房洞室为背景工程，研究了设计地震动作用下节理岩体结构效应对地下洞室地震响应的影响，得到了一些初步的结论。

2 基本原理

2.1 二维节理网络的生成

在现场实测资料的基础上生成岩体的节理网络，是现场统计实测过程的逆过程。现场实测统计过程根据岩体结构形式求得结构面几何参数的分布函数形式，即建立结构面的概率模型过程。而节理网络的生成是根据实测统计确立的结构面几何参数的概率模型求得服从这一模型的几何图形。

进行节理网络模拟的时确定节理的形态是非常重要的，但由于节理的形成是一个复杂的地质过程，对节理形成的机制至今不是十分清楚，观察资料相对较少，又考虑到简化理论的缘故，将节理的形态简化为圆形或椭圆形是一个较合理的做法。

Baechar 模型是一个典型的圆盘模型[9]，见图1。该模型中节理的尺寸是有限的，每一个节理的定位由中心点、半径、产状（倾角和倾向）3个参数决定。中心点在三维空间内是均匀分布的，半径和产状可为常数或由一个概率分布函数决定。

在由三维空间退化至二维平面（统计窗）时，3个参数退化为节理密度（中心点）、迹长、视倾角。

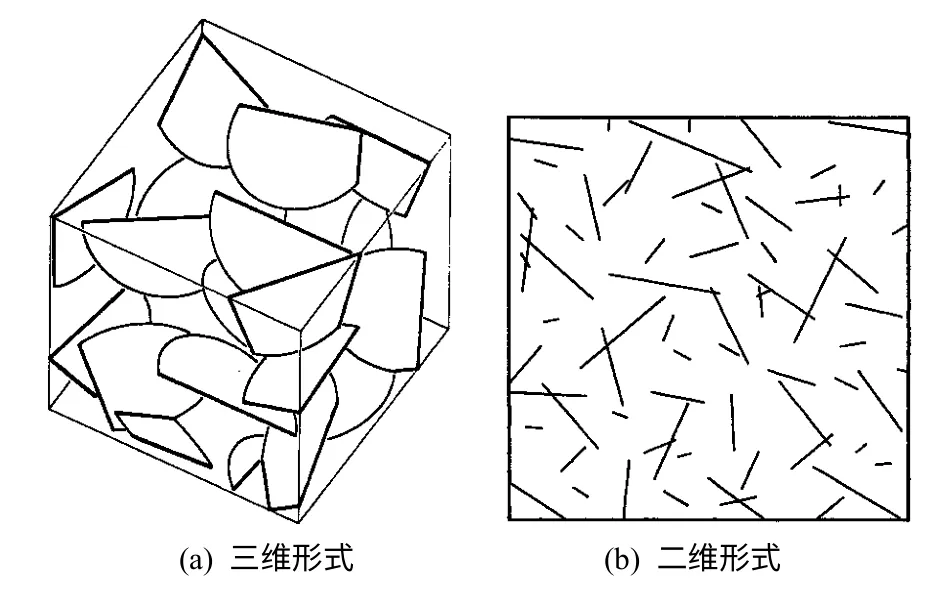
图1 Baechar 节理网络模型示意图Fig.1 Sketches of 3D and 2D joint network of Baechar model

2.2 节理岩体结构效应的表征参数

大量的统计资料表明，节理岩体结构面的几何参数（结构效应参数）服从一定的分布规律。人工模拟生产节理网络时，对这些几何参数分布规律的变化对地震作用下的最大位移的影响进行考察，认为表示了节理岩体结构效应对洞室地震响应的影响。

（1）节理密度

Baecher 圆盘模型认为节理是空间的圆盘，且圆盘中点是三维齐次Poisson 点过程。一般来说，裂隙的条数依据其密度服从Poisson 随机过程；裂隙中心点位置服从研究域内的均匀分布[10]。密度的定义方法有多种，如单位面积内节理的条数（1/m2）、单位面积内节理的迹长和（1/m）、单位面积内迹长和与面积的平方根之比（单位为1）等等。注意到单位面积内迹长之和与面积的平方根之比指标是与尺寸无关的，不受节理岩体尺寸效应的影响，故此处将其做为节理的密度参数。

（2）节理倾角

除倾角角度外，倾角的离散分布形式也是非连通随机节理岩体中的一个重要指标。节理产状在二维平面上退化为视倾角一个参数。在描述倾角发育规律的概率模型中，Fisher 分布被广泛使用[11]，Fisher 分布假定：在一组节理内，围绕最大概率方向的节理具有以下的密度函数：

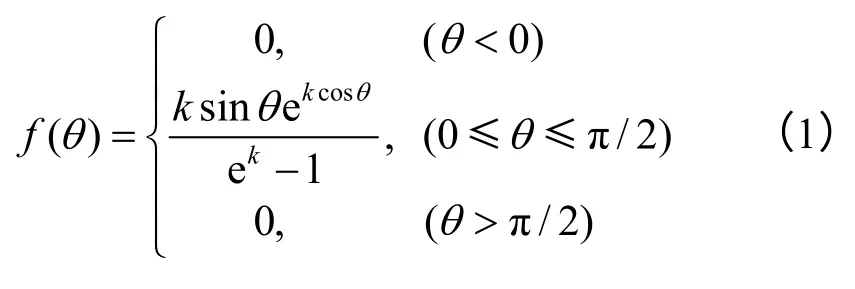
相应的概率分布函数为

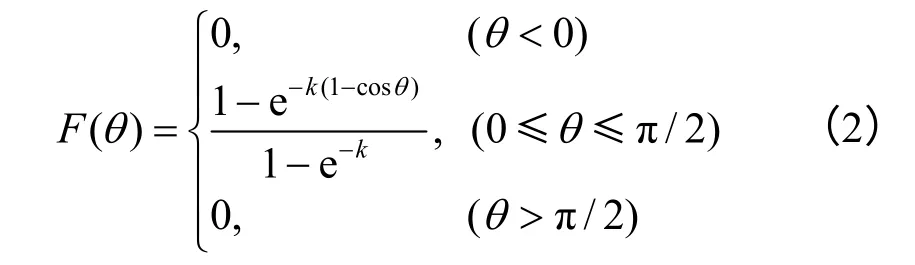
式中：Fisher 分布常数k 反映了节理的离散程度，称为离散系数，k 越大，则节理倾角分布越密集，即数据点越向平均方向集中；θ为节理倾角与最大概率方向的交角。图2为不同Fisher 常数时节理倾角分布散点图。

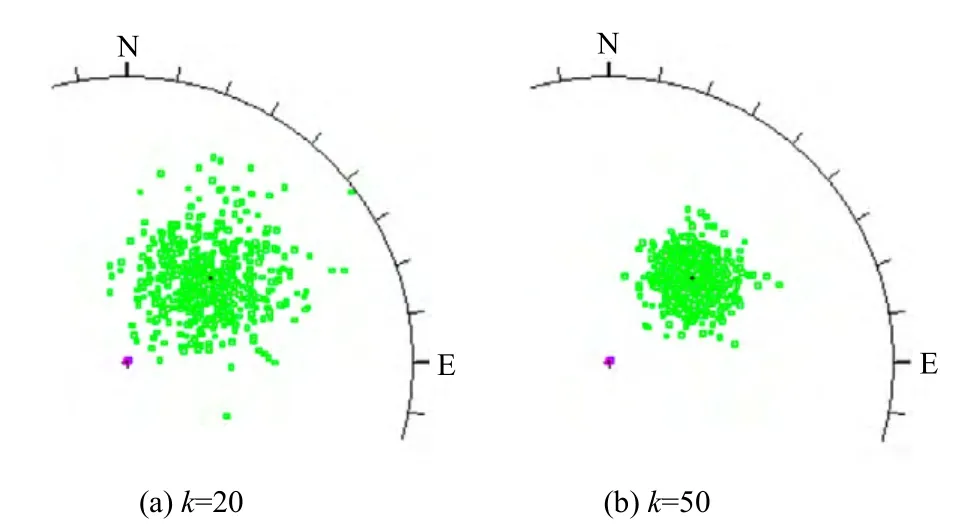
图2 不同Fisher 常数时节理倾角分布散点图Fig.2 Stereonet plots by different values of Fisher k

（3）节理迹长

与倾角指标类似，除迹长长度指标外，迹长的离散分布形式也是非连通随机节理岩体中的一个重要指标。对于迹长离散程度的分布形式，不同学者提出了不同的分布形式，如负指数分布、正态分布、对数正态分布、Γ 分布等[12]。在对分布函数不做更多讨论的前提下，为了简化起见此处选取参数较少的正态分布表达节理迹长的离散程度，见式（3）。节理迹长离散程度即由标准差σ 表征。正态分布概率密度函数的定义域本为[+∞,-∞]，但有大于99%的数据位于均值 ±3σ 的的范围内，在此以3σ 区间作为迹长分布的上下限：

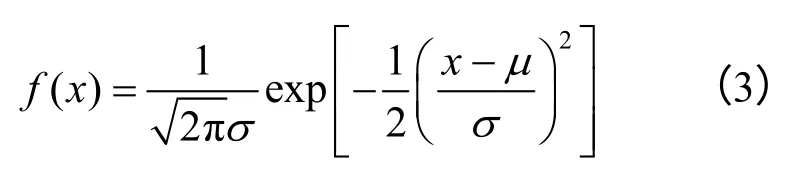
综上，本文采用随机节理密度、随机节理倾角角度、随机节理倾角离散程度、随机节理迹长长度、随机节理迹长离散程度五方面讨论了随机岩体的结构效应对地下洞室群地震响应的影响。

2.3 节理网络生成中随机性问题的处理

对于具有一定统计特征的现场节理分布，在数值模拟过程中可以生成无数个与之相对应的节理网络模型。随机节理岩体的节理网络，按照现场节理统计规律生成，具有随机性。由不同的随机过程，可以得到不同的节理网络图。不同的节理网络图形成的节理岩体表现出的力学性质必然也是随机的、不相同的。不能将任一节理网络图反映的计算结果，看成具有相应节理统计规律岩体的确定性结果。节理岩体的力学性质应该由多个节理网络模型所计算的力学性质的平均。计算中，每种计算方案生成10种随机节理网络样本，取样本计算结果的平均值作为该随机分布下节理岩体的结果。

3 结构效应对洞室地震响应的影响

3.1 数值模拟条件

大渡河流域大岗山水电站地下厂房洞室群采用主副厂房、主变室、尾水调压室三大洞室平行布置。主厂房开挖跨度为30.80 m。场址工程区域地形地貌复杂，区域地应力水平较高，地质条件复杂，地震威胁强烈，设计地震动加速度水准高达3.36 m/s2。本文以本工程主厂房典型剖面为例，采用随机节理网络有限元方法研究节理的结构效应对地下洞室地震响应的影响。

根据设计单位提供的开挖揭示地质资料，厂区揭露的节理裂隙上限为10 m 级。将节理岩体视为岩石与结构面的组合，其力学参数参照地下厂房区现场钻孔弹模测试结果依经验取值见表1。据反演值，厂区地应力主应力分量分别约为13、11、5 MPa。

对于每一个计算方案，在分10 步开挖完洞室后分别按地震波从左侧入射和右侧入射，采用波动场应力法[13]进行地震响应计算。

表1 节理岩体中岩石与结构面力学参数Table 1 Mechanical parameters of rock and joints

3.2 随机节理密度

为研究节理密度变化对地下洞室地震响应的影响，取节理密度为10，50，100，150，200，对于每级节理密度取10个样本，取10个样本计算得到的最大位移平均值作为该级节理密度下洞室群的最大位移；节理倾角均值为45°，服从Fisher 分布，Fisher 分布常数k为中值30。节理迹长服从正态分布，迹长均值为15 m，标准差σ=2 m，3分布区间为[9,21]m。

图3为节理密度分别为50和150 的2个节理网络模型样本的示意图。

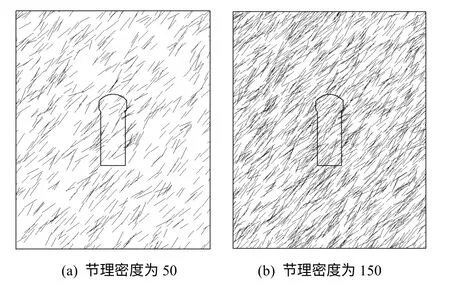
图3 不同节理密度的随机节理岩体及地下洞室示意图Fig.3 Sketches of joint network and underground cavern plot of different joint densities

图4为洞室群开挖位移与不同节理密度的关系。图5为洞室群地震最大位移响应与不同节理密度的关系。从图中可见，当地震波从左侧入射的时候，即地震波入射方向与二维平面上节理的视倾角相反的时候，洞室地震位移大于地震波从右侧入射，且此时洞室开挖位移与地震位移规律相同。随节理密度增加，即单位面积内迹长之和与面积的平方根之比的增加，洞室的地震位移呈现明显的增加趋势。当节理密度由10 增加到200 的时候，最大地震位移由0.27 cm 增加到3.4 cm。对比地震波至左侧和右侧入射产生的地震位移，可知最大地震位移发生在地震波入射方向与随机节理的视倾向相反时，且随节理密度增加，两个方向入射的地震波产生的最大地震位移差距越大。

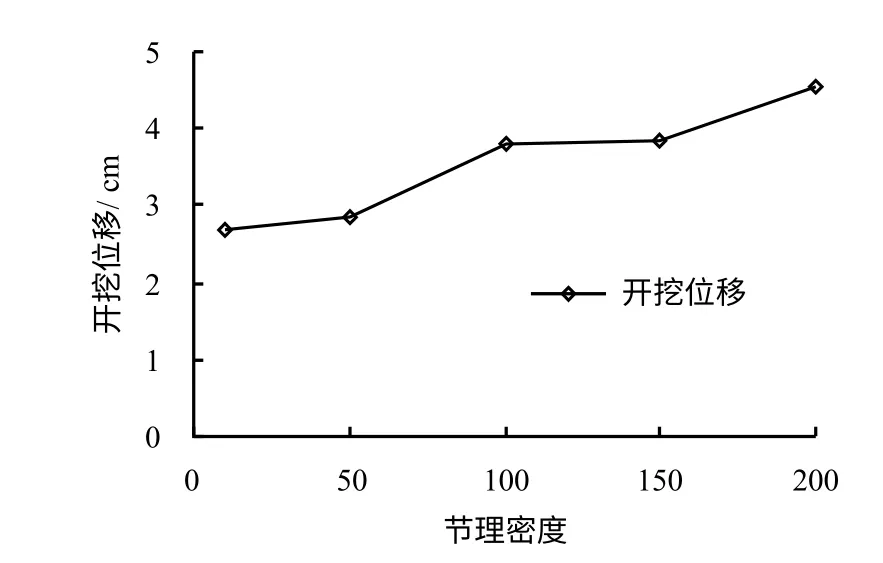
图4 洞室开挖位移与节理密度的关系Fig.4 Relationship between seismic displacement and joint density

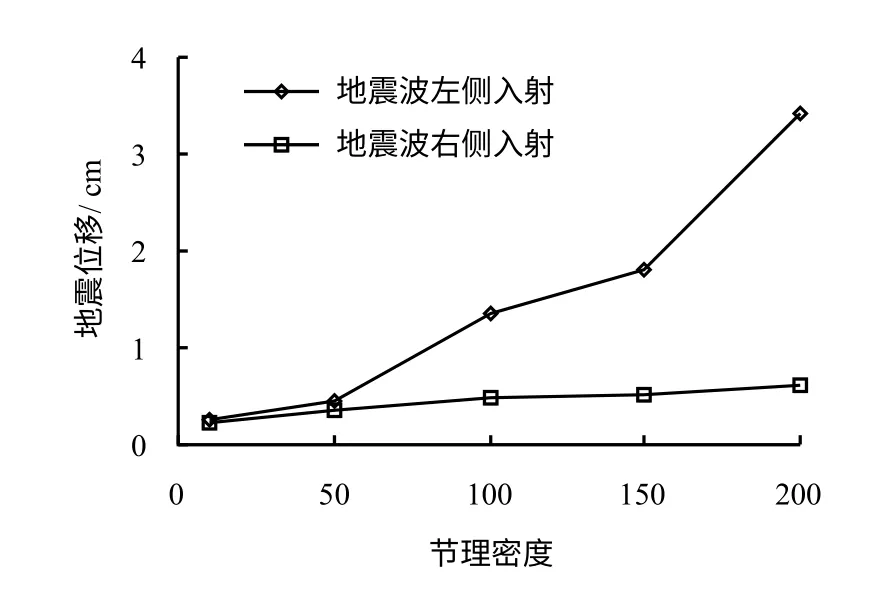
图5 洞室地震位移与节理密度的关系Fig.5 Relationships between seismic displacement and joint density in cavern

3.3 随机节理倾角角度的影响

研究当节理倾角变化对地下洞室群地震响应的影响时，为了减小倾角离散程度对结果可能的影响，此处Fisher 常数取为高值50；取节理倾角均值分别为0°、15°、30°、45°、60°、75°、90°。对于每级节理倾角取10个样本，计算得到的最大位移平均值作为该级节理倾角下洞室的最大位移。节理迹长服从正态分布，迹长均值为15 m，标准差σ=2 m，3σ分布区间为[9,21]m；节理密度取为中值100。图6为节理倾角分别为15°和75°的两个节理网络模型样本的示意图。

图6 不同节理倾角的随机节理岩体及地下洞室示意图Fig.6 Sketches of Joint network and underground cavern plot of different joint orientations

图7为洞室群开挖位移与不同节理倾角的关系，图8为洞室地震最大位移响应与不同节理倾角的关系。从图中可见，当地震波从左侧入射的时候，即地震波入射方向与二维平面上节理的视倾角相反的时候，洞室地震位移大于地震波从右侧入射，且此时洞室开挖位移与地震位移规律相同。当节理倾角在0°～80°范围内时，随节理倾角增加，洞室的地震位移呈现较明显的增加趋势，且增加趋势在30°～60°范围内特别明显。当节理倾角由0°增加到80°时，最大地震位移由0.6 cm 增加到2.3 cm。而当节理倾角为90°时，洞室的地震位移较80°时更小，表明陡倾角节理对洞室地震稳定性的威胁比垂直节理更大。对比地震波至左侧和右侧入射产生的地震位移，可见当节理处于水平（0°）和垂直角度（90°）时，地震波入射方向对洞室地震位移基本无影响，另可发现，当地震波入射方向与随机节理的视倾向反向时地震位移更大，节理倾角越大，这个趋势越明显。

图7 洞室开挖位移与节理密度的关系Fig.7 Relationship between seismic displacement and joint density in cavern

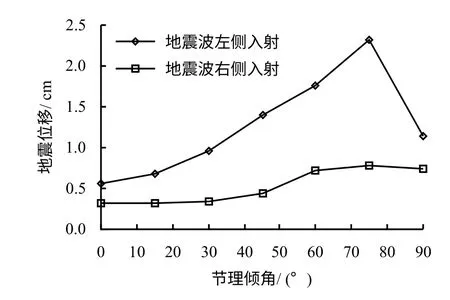
图8 洞室地震位移与节理倾角的关系Fig.8 Relationship between seismic displacement and joint orientation

3.4 随机节理倾角离散程度的影响

为了研究节理倾角离散程度对地下洞室地震响应的影响，分别取Fisher 常数为5、10、20、30、40、50，对每级Fisher 常数取10个样本，计算得到的最大位移平均值作为该级倾角离散程度下洞室的最大位移；节理倾角均值为中值45°；节理迹长服从正态分布，迹长均值为15 m，标准差σ=2 m，3σ 分布区间为[9,21]m，节理密度取为中值为100。

图9为Fisher 常数分别为10和40 的2个节理网络模型样本的示意图。

图9 不同节理倾角离散程度的随机节理岩体及地下洞室示意图Fig.9 Sketches of random joint network rock and underground cavern plot of different joint orientation discretizations

图10为洞室群开挖位移与不同节理倾角离散程度的关系，图11为洞室地震最大位移响应与不同节理倾角离散程度的关系。从图中可见，当地震波从左侧入射的时候，即地震波入射方向与二维平面上节理的视倾角相反的时候，洞室地震位移大于地震波从右侧入射，且此时洞室开挖位移与地震位移规律相同。当在Fisher 常数小于20 时，随节理倾角离散程度减小，洞室的地震位移呈现减小的趋势，但影响程度较小，约在1 cm 左右；当Fsiher 常数大于20 后，节理倾角的离散程度对洞室的地震位移基本无影响，地震波入射方向与随机节理的视倾向反向时，地震位移更大，但节理倾角离散程度对这个趋势基本无影响。

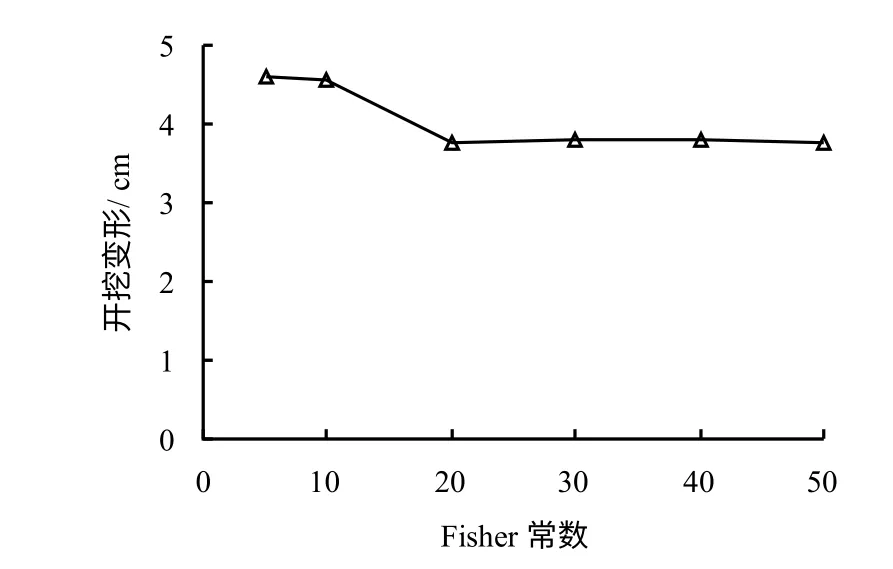
图10 洞室开挖位移与节理密度的关系Fig.10 Relationship between seismic displacement and joint density

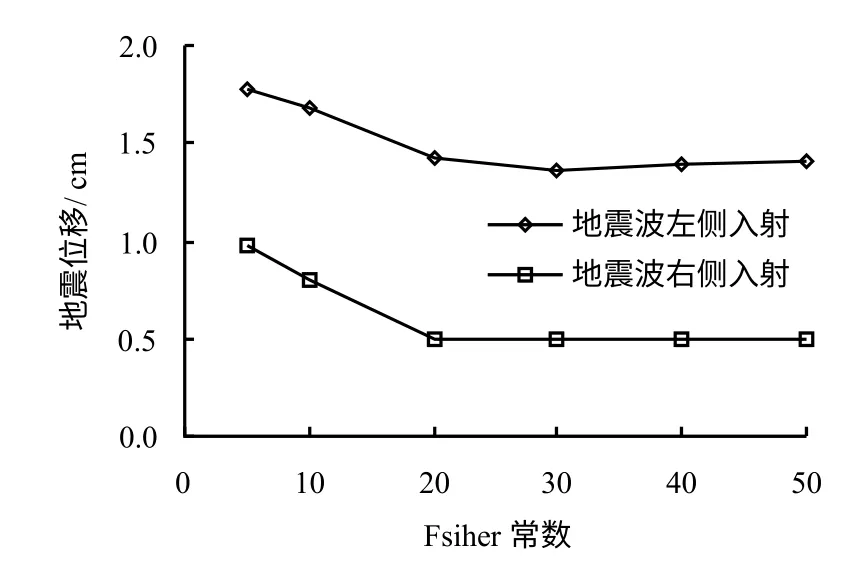
图11 洞室地震位移与节理倾角离散程度的关系Fig.11 Relationships between seismic displacement and joint orientation discretization

3.5 随机节理迹长长度的影响

为了研究节理迹长变化对地下洞室地震响应的影响，分别取节理迹长定值为5、10、15、20、25 m，对每级迹长取10个样本，计算得到的最大位移平均值作为该级节理迹长下洞室的最大位移。节理倾角均值为中值45°，服从Fisher 分布，Fisher 分布常数为中值30，节理密度取为中值100。

图12为节理迹长分别为10 m和20 m 的2个节理网络模型样本的示意图。

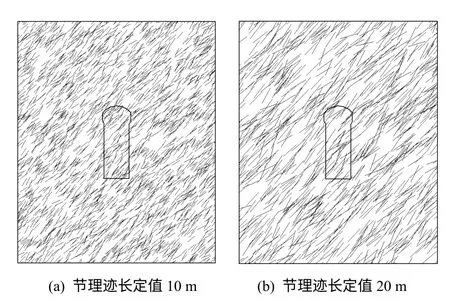
图12 不同节理迹长的随机节理岩体及地下洞室示意图Fig.12 Sketches of joint network rock and underground cavern plot of different joint trace lengths

图13为洞室群开挖位移与不同节理迹长的关系，图14为洞室群地震最大位移响应与不同节理迹长长度的关系。从图中可见，地震波从左侧入射时，即地震波入射方向与二维平面上节理的视倾角相反时洞室地震位移大于地震波。从右侧入射，此时洞室开挖位移与地震位移规律相同。随节理迹长长度的增加，洞室的地震位移呈现较明显的增加趋势，增加趋势随节理迹长长度的增加逐渐减小，当节理长度大于25 m 后，对洞室地震最大位移基本无影响。仍可发现，当地震波入射方向与随机节理的视倾向反向时，地震位移更大，且节理倾角越大趋势越明显。

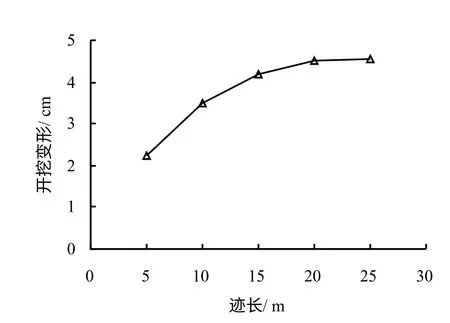
图13 洞室开挖位移与节理密度的关系Fig.13 Relationship between seismic displacement and joint density

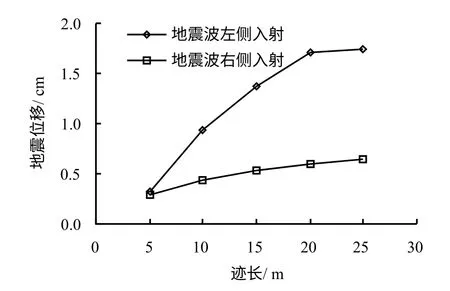
图14 洞室地震位移与节理迹长的关系Fig.14 Relationships between seismic displacement and joint trace length

3.6 随机节理迹长离散程度的影响

为了研究节理迹长离散程度对地下洞室地震响应的影响，对于迹长均值为15 m 时，分别取正态分布区间为[15,15]m（标准差=0 m）、[12,18]m（标准差=1 m）、[9,21]m（标准差=2 m）、[6,24]m（标准差=3 m）、[3,27]m（标准差=4 m），(0,30]m（标准差=5 m，但下限不能为0）。每级节理迹长离散程度取10个样本，计算得到的最大位移平均值作为该级迹长离散程度下洞室的最大位移。节理倾角均值为中值45°，服从Fisher 分布，Fisher 分布常数为中值30，节理密度取为中值100。图15为节理迹长分布区间分别为[9,21]m和[3,27]m的2个节理网络模型样本的示意图，图16为洞室群开挖位移与不同节理迹长离散程度的关系，图17为洞室的地震位移响应与不同节理迹长离散程度的关系。从图中可见，当地震波从左侧入射，即地震波入射方向与二维平面上节理的视倾角相反时，洞室地震位移大于地震波，从右侧入射，且此时洞室开挖位移与地震位移规律相同。节理迹长离散程度对洞室地震位移影响较小。节理标准差由0 m 增加至5 m 时，地震位移基本无变化。仍可发现，当地震波入射方向与随机节理的视倾向反向时地震位移更大，但这个趋势与迹长离散程度无关。

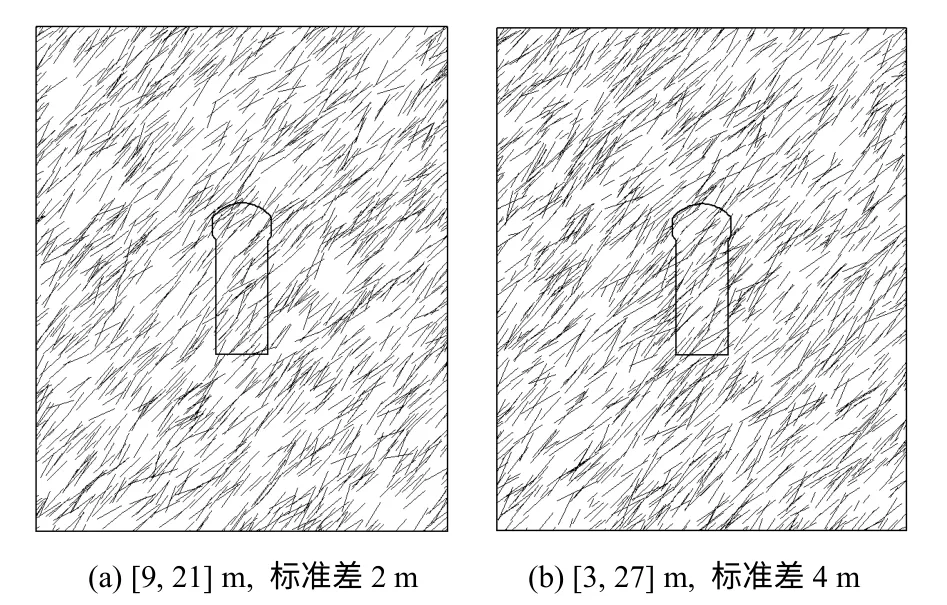
图15 不同节理迹长离散程度的随机节理岩体及地下洞室示意图Fig.15 Sketches of random joint network rock and underground cavern plot of different joint trace length discretizations

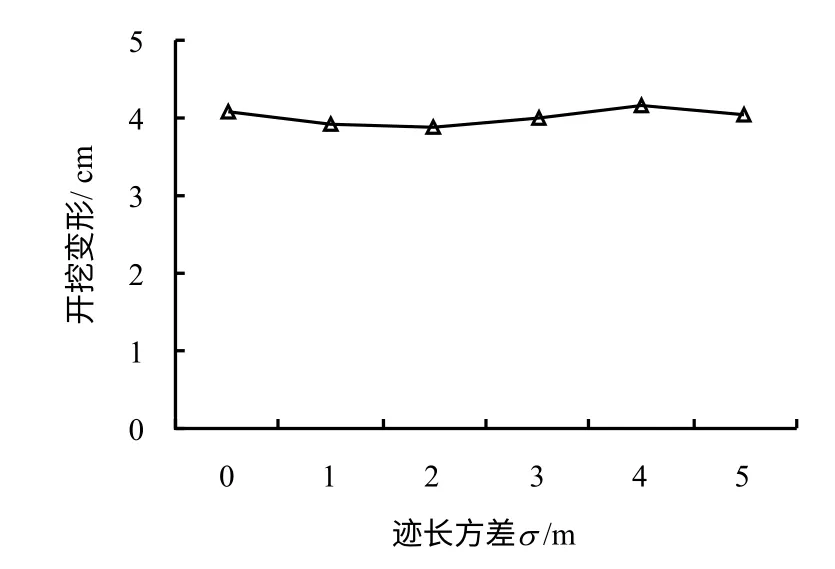
图16 洞室开挖位移与节理密度的关系Fig.16 Relationship between excavation displacement and joint density

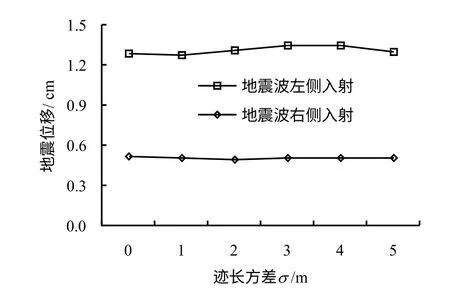
图17 洞室地震位移与节理迹长离散程度的关系Fig.17 Relationships between seismic displacement and joint trace length discretization

4 结论

（1）采用二维随机节理网络有限元研究节理岩体结构效应对地下洞室地震响应的影响是可行的。节理岩体的结构效应可用随机节理密度、随机节理倾角角度、随机节理倾角离散程度、随机节理迹长长度、随机节理迹长离散程度5个参数表征。

（2）在相同地震动作用下，对于节理密度，随节理密度增加，洞室的地震位移呈现明显的增加趋势。对于节理倾角角度，当节理倾角在0°～80°范围内时，随节理倾角增加，洞室的地震位移呈现较明显的增加趋势，当节理倾角为90°时，洞室的地震位移却较80°时更小。对于节理倾角离散程度，当节理离散程度较大，即Fisher 常数在20 以下时，洞室地震位移随节理倾角离散程度减小，洞室的地震位移呈现减小的趋势，节理离散程度较小，即Fisher 常数大于20 后，节理倾角的离散程度对洞室的地震位移基本无影响；随节理迹长长度的增加，洞室的地震位移呈现较明显的增加趋势，但这个增加趋势随节理迹长长度的增加逐渐减小，当节理长度大于25 m 后，节理长度对洞室地震最大位移的基本无影响；节理迹长离散程度对洞室地震位移影响较小。

（3）采用波动场应力法对随机节理岩体洞室进行地震响应分析的过程中发现，无论随机节理的结构效应如何，总是当地震波入射方向与二维平面上节理的视倾角相反的时候，地震位移更大。

本文仅采用了1 组二维节理研究了节理岩体的结构效应对洞室地震响应的影响，所得到的结论是初步的，在后续的研究中可进一步考虑多组随机节理的影响，采用三维节理网络有限元进行研究。此外，对于节理的力学参数及节理岩体的结构效应与尺寸效应对地下洞室地震响应的影响，有待于进一步考虑。

[1]黄润秋,徐模,陈剑平,等.复杂岩体结构精细描述及其工程应用[M].北京:科学出版社,2004.

[2]王平.节理岩体的等效连续模型与工程应用[博士学位论文D].武汉:中国科学院武汉岩土力学研究所,1999.

[3]蓝航,姚建国,张华兴,等.基于FLAC3D的节理岩体采动损伤本构模型的开发及应用[J].岩石力学与工程学报,2008,27(3):572－579.LAN Hang,YAO Jian-guo,ZHANG Hua-xing,et al.Development and application of constitutive model of jointed rock mass damage due to mining based on FLAC3D[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(3):572－579.

[4]张强勇.多裂隙岩体三维加锚损伤断裂模型及其数值模拟与工程应用研究[博士学位论文D].武汉:中国科学院武汉岩土力学研究所,1998.

[5]谷宁,张运良.节理参数对水电站地下洞室围岩地震反应的影响研究[J].水电能源科学,2012,30(1):80－83.GU Ning,ZHANG Yun-liang.Research on influence of joint parameters on seismic response of underground chamber for hydropower station[J].Water Resource and Power,2012,30(1):80－83.

[6]张丽华,陶连金,李晓霖.节理岩体地下洞室群的地震动力响应分析[J].世界地震工程,2002,18(2):158－163.ZHANG Li-hua,TAO Lian-jin,LI Xiao-lin.Dynamic response analysis of large underground excavations in jointed rock[J].World Earthquake Engineering,2002,18(2):158－163.

[7]HAMMAH R E,YACOUB T,CORKUM B.The practical modelling of discontinuous rock masses with finite element analysis[C]//Proceedings of the 42nd U.S.Symposium on Rock Mechanics and the 2nd U.S.-Canada Rock Mechanics Symposium.San Francisco,California:[s.n.],2008

[8]周维垣,杨强.岩石力学数值计算方法[M].北京:中国电力出版社,2005.

[9]DERSHOWITZ W.Rock joint systems[ph.D].Cambridge,MA.:Massachusetts Institute of Technology,1985.

[10]张国强,费文平,张茹,等.节理泊松圆盘模型直径分布推断的解析方法[J].岩土力学,2011,32(4):1149－1157.ZHANG Guo-qiang,FEI Wen-ping,ZHANG Ru,et al.Analytical method for estimating diameter distribution of Poisson disc joint model[J].Rock and Soil Mechanics,2011,32(4):1149－1157.

[11]陆峰,王俊奇.Fisher 模型在岩体裂隙面模拟中的应用[J].中国水利水电科学研究院学报,2010,8(4):309－314.LU Feng,WANG Jun-qi.Application of Fisher model in rock fracture simulation[J].Journal of China Institute of Water Resources and Hydropower Research,2010,8(4):309－314.

[12]金曲生,王思敬,陈昌彦.估计迹长概率分布函数的新方法及其应用[J].工程地质学报,1997,5(2):150－155.JIN Qu-sheng,WANG Si-jing,CHEN Chang-yan.A new method for estimating probability distribution function of trace length and its application[J].Journal of Engineering Geology,1997,5(2):150－155.

[13]张志国.地下洞室群地震响应数值分析方法研究[博士学位论文D].武汉:武汉大学,2012.