基于复杂地质体的地应力场智能识别方法研究

李茂辉，杨志强，高 谦，翟淑花，王有团

（1.北京科技大学 土木与环境工程学院，北京 100083；2.北京科技大学 金属矿山高效开采与安全教育部重点实验室，北京 100083；3.金川集团股份有限公司，甘肃 金昌 737100；4.北京市地质研究所，北京 100120）

1 引言

地质体经历了漫长的地质构造运动和多次地质改造作用，在地层内封存不同时期的残余构造作用力。不同地质体受到不同地质作用类型、作用程度、作用时间和经历次数的不同，导致地质体的地应力大小和方向在空间和时间上存在变异性[1－2]。地应力测量仍是目前地应力研究的最重要手段，但由于受时间和经费的限制，大部分工程的地应力测量数量十分有限，且受测量手段和方法等因素的影响，由此所获得的地应力测试结果往往存在着很大程度的离散性，从而给地应力场分布规律研究带来很大困难[3－5]。为了提高地应力场研究的可靠性，20 世纪80年代首次提出了黏弹性位移反分析法，通过开挖工程的变形监测进行岩体力学参数与地应力反演[6]。随着人工智能技术的发展，人们开展了大量的基于神经网络与数值计算相结合的地应力反演研究[7－12]。近年来，人们利用地质构造形迹以及围岩的变形破坏特性估算地应力场的大小和方向。由于神经网络的地应力反演是对有限地应力实测结果的训练和预测，或者是借助于数值模型扩大地应力样本而提高地应力的预测精度，因此，现有的地应力反演还存在一定局限性。本文针对某铜镍矿复杂地质体，建立了三维正交数值模型，利用遗传规划[13－15]建立了监测点地应力和与原岩参数和侧压系数的关系和地应力计算值与实测值之差的平方和最小为目标优化模型，采用遗传算法[16－17]对目标函数进行优化求解，得到原岩参数和侧压系数，代入三维数值模型中即可获得复杂地质体的初始应力场。

2 地应力智能识别模型图

针对某复杂地质体的地应力场，基于如图1 所示的地应力智能识别方法流程图顺序，根据现有地应力测试数据，使用Flac3D、遗传算法和遗传规划等工具对地应力场进行智能反演。

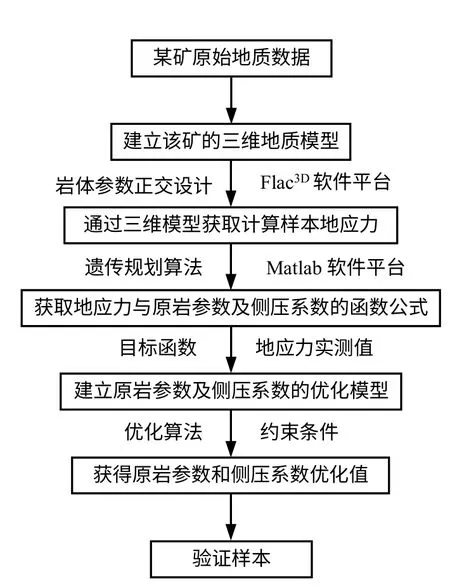
图1 地应力智能识别方法流程图Fig.1 Flowchart of in-situ stress intelligent identification methods

3 地质体三维正交数值模型

某铜镍矿初始地应力反演区域矿床主要为超基性岩型硫化铜镍矿床，主体构造为倾向南西的单斜构造，矿区水平构造应力较高，节理裂隙较为发育。为简化模型，在模型的建立过程中未考虑节理裂隙对地应力的影响。

3.1 Flac3D 模型的建立

基于Flac3D软件平台，借助于已有矿床的水平与垂直地质剖面图建立三维地质模型（见图2），将地质体划分围岩和矿体。图中，水平面指向东为x 坐标，指北为y 坐标，垂直向上为z 坐标建立坐标系统。

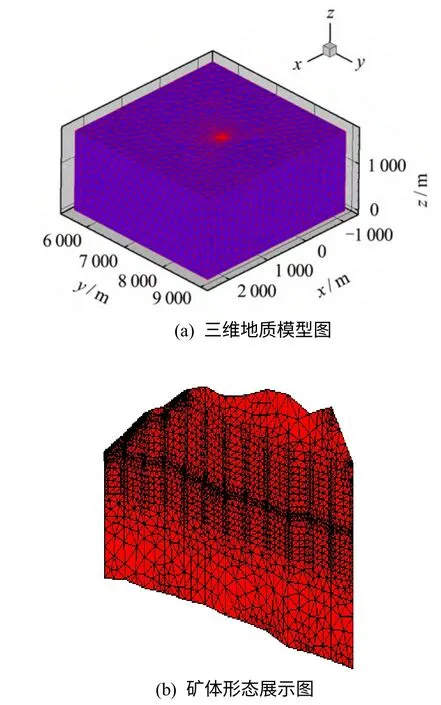
图2 某铜镍矿三维地质模型图Fig.2 3D geological model of a copper-nickel mine

3.2 地质体岩体参数的选择

复杂地质体的岩体参数可由地质体的重力和构造应力 λ1、λ2（x、y 方向的侧压系数）、矿体重度、弹性模量和泊松比8个因素表征，采用8 因素2 水平的正交数值分析模拟不同组合条件下地应力场的正交试验方案见表1。表中，γ1、E1、μ1分别为围岩的重度、弹性模量和泊松比；γ2、E2、μ2分别为矿体的重度、弹性模量和泊松比；λ1、λ2分别为x、y 方向的侧压系数。

3.3 地应力测点的选择

不同工程的地质体由于受工程类型、重要程度以及时间与经费的限制，开展现场的地应力测量的方法和数量存在差异。考虑到地应力识别的工作量，应考虑到测点位置、深度、岩性和断层等因素，进行有选择性的采用实测地应力数据，并且尽可能选择地应力监测手段比较可靠的监测结果。表2 列出测点位置和地应力测试结果，其中前5个作为训练样本，后4个作为检验样本。

3.4 地应力的计算

采用建立的三维数值模型，根据正交试验方案，进行12 次三维数值计算，提取训练样本对应的地应力分量，共计60 组数据，计算结果见表3。限于篇幅，本文只列出第一个测点的计算应力值。

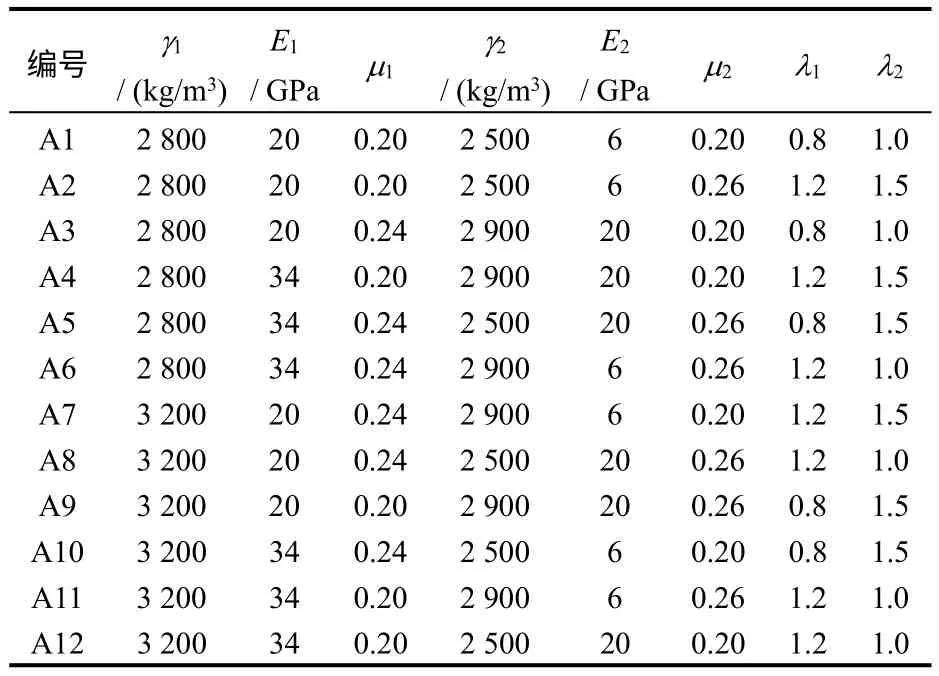
表1 某铜镍矿地质体正交试验方案Table 1 Orthogonal test of geological bodies

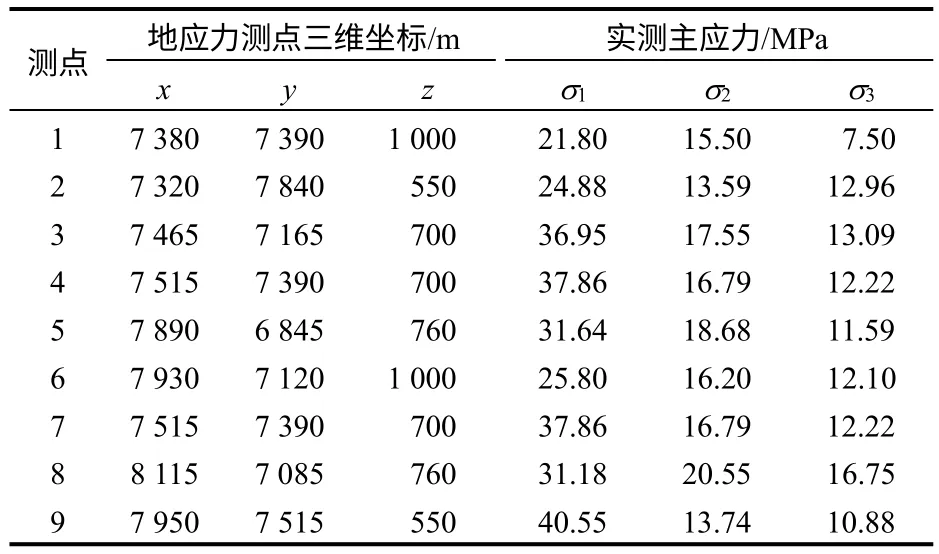
表2 地应力测点位置和实测值Table 2 Positions of measuring points and measured values of in-situ stress

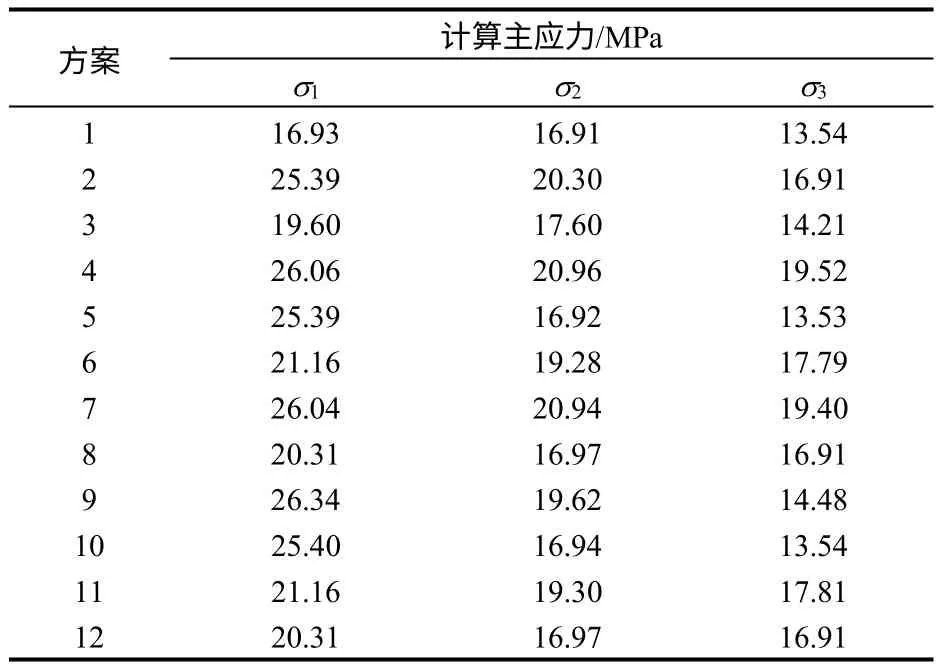
表3 地应力测点各方案计算值Table 3 Calculated values of in-situ stress

4 地应力智能识别模型建立

4.1 遗传规划的基本原理

遗传规划[18－19]是从遗传算法中发展起来的一种全局寻优技术，借鉴生物界中进化与遗传的机制，遵循“优胜劣汰，适者生存”的原则发展起来的一种计算方法，目前已经成为继专家系统、人工神经网络之后的有关人工智能学科的第三个研究点。遗传规划是一种自适应编程技术，擅长于对模型结构的自动搜索，能够自己生成初始搜索空间，具有适应性强、精度高、受主观因素影响小等优点。

4.2 地应力与原岩参数和侧压系数的函数关

根据正交试验方案和表4 获得的地应力计算值，利用遗传规划程序建立地应力计算值和原岩参数及侧压系数之间的函数关系：

遗传规划相关参数见表4，经过多次寻优，得到图3（部分）所示的最佳遗传树。

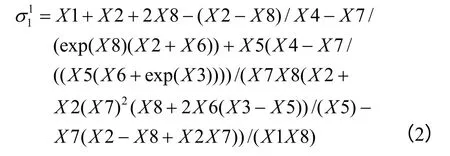
式中：X1、X2、X3、X4、X5、X6、X7、X8分别为矿体的密度、弹性模量、泊松比、围岩的密度、弹性模量、泊松比和侧压系数。

表4 遗传规划的控制参数Table 4 Control parameters of genetic programming

图3 测点1 最大主应力最佳遗传树Fig.3 Best individual tree genetic programming model obtained

5 地应力的智能识别与反演

5.1 地应力智能识别优化模型

根据地质体中5个测点的地应力计算值与实测值之差的平方和达到最小为优化目标，建立原岩应力和侧压系数的优化模型，目标函数如下：

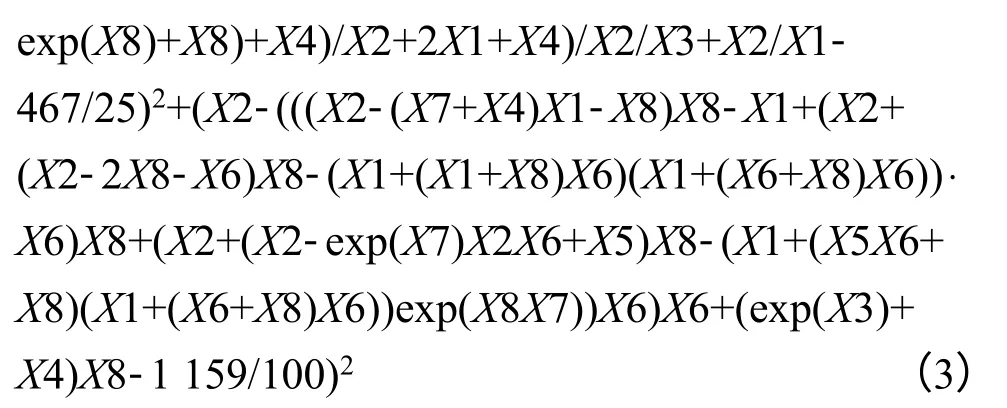
根据矿体和围岩的性质，建立约束条件：2.4＜γ1＜2.8，2.8＜γ2＜3.6；6＜E1＜20，20＜E2＜34；0.2＜μ1＜0.26，0.2 ＜ μ2＜0.24；0.5＜λ1＜1.2，1.1＜ λ2＜1.5。

5.1.1 遗传算法基本原理

遗传算法与传统搜索算法不同，以适应度函数为依据，通过对种群中的所有个体实施遗传操作，实现群体内结构重组的迭代过程随机搜索算法。选择、杂交、变异构成遗传算法的3个主要遗传操作因子[20－21]。

5.1.2 地质体原岩参数和侧压系数的优化

利用遗传算法强大的全局搜索能力，设置遗传算法各参数值（见表5），然后遵从遗传算法下述遗传操作：随机产生初始群体→个体适应度评价→选择操作→交叉操作→变异操作→终止法则（最大遗传代数）。由此获得地质体的原岩参数和侧压系数，即围岩参数、矿体参数和侧压系数见表6。

表5 遗传算法参数表Table 5 Control parameters of genetic algorithm

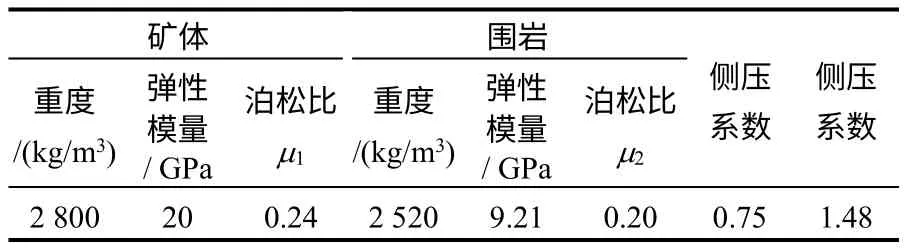
表6 基于智能识别的围岩体参数及测压系数Table 6 Results based on the intelligent identification methods

5.2 地质体地应力场反演

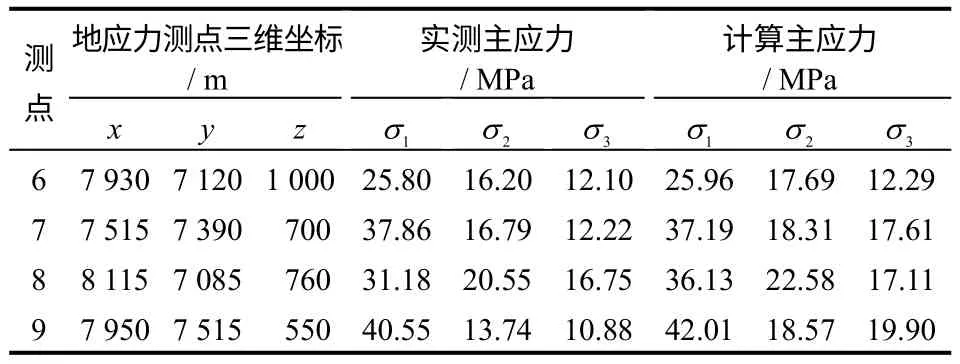
表7 地应力实测值和计算值对比Table 7 Comparison between measured values and calculated values of in-situ stress

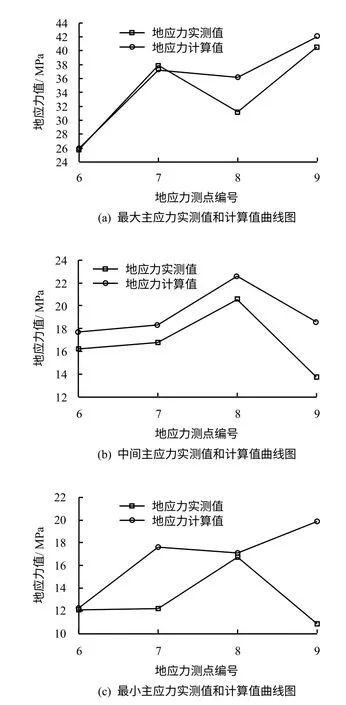
图4 地应力实测值和计算值对比曲线Fig.4 Contrast curves of measured and calculated values of in-situ stress

由图4 可见，地应力计算值较高于实测值，除了测点7、9 的最小主应力计算值与实测值的误差比较大以外，最大主应力和中间主应力计算值较实测值的相对误差都在工程允许范围内；测点7、9位于矿体边缘，周边地质在形成过程中经受构造变动、边缘冷却、热液等活动的影响，矿体边缘及内部易形成构造性破碎及片岩带，建模过程并未考虑此类因素影响，所得地应力理论计算结果与实测值存在一定差异。

5 结语

针对复杂的地质体，建立了三维正交数值模型，利用遗传规划建立了地应力与原岩参数和侧压系数的函数关系,获得初始地应力场。验证数据结果显示，初始地应力场的准确性是可靠的，获得地应力的方法是行之有效的。

利用遗传规划中的复制、交叉和突变等遗传操作，获得最能符合地应力与原岩参数和侧压系数关系的函数，结果显示，遗传规划的精度能够很好地满足要求。

采用遗传算法强大的全局搜索能力，优化已经建立的目标函数，获得了原岩参数和侧压系数，结果显示，主应力实测值和计算值的误差是在合理范围内，可以证明获得的某铜镍矿的初始应力场是可靠的。

根据某铜镍矿实测地应力值，结合三维正交数值模型、遗传规划和遗传算法研究方法，识别和反演复杂地质体的初始地应力，为以后矿区地应力的研究和准确获得提供了一种较为可信的研究思路。

[1]蔡美峰.岩石力学与工程[M].北京:科学出版社,2002.

[2]廖椿庭,施兆贤.金川矿区原岩应力实测及在矿山设计中的应用[J].岩石力学与工程学报,1983,2(1):103－112.LIAO Chun-ting,SHI Zhao-xian.In-situ stress measurements and their application to engineering design in the Jinchuan mine[J].Chinese Journal of Rock Mechanics and Engineering,1983,2(1):103－112.

[3]蔡美峰,乔兰,于波,等.金川二矿区深部地应力测量及其分布规律研究[J].岩石力学与工程学报,1999,18(4):414－418.CAI Mei-feng,QIAO Lan,YU Bo,et al.Results and analysis of in-situ stress measurement at deep position of No.2 mining area of Jinchuan nichkel mine[J].Chinese Journal of Rock Mechanics and Engineering,1999,18(4):414－418.

[4]蔡美峰,刘卫东,李远.玲珑金矿深部地应力测量及矿区地应力场分布规律[J].岩石力学与工程学报,2010,29(2):227－233.CAI Mei-feng,LIU Wei-dong,LI Yuan.In-situ stress measurement at deep position of Linglong gold mine and distribution law of in-situ stress field in mine area[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(2):227－233.

[5]丰成君,陈群策,谭成轩,等.广东核电站地应力测量及其应用[J].岩土力学,2013,34(6):1745－1752.FENG Cheng-jun,CHEN Qun-ce,TAN Cheng-xuan,et al.In-situ stress measurement and its application to Guangdong nuclear power stations[J].Rock and Soil Mechanics,2013,34(6):1745－1752.

[6]李云鹏,王芝银.黏弹性位移反分析的边界元法[J].西安矿业学院学报,1989,1(1):17－24.LI Yun-peng,WANG Zhi-yin.The boundary element method of back analysis of viscoelastic displacements[J].Journal of Xi’an Mining Institute,1989,1(1):17－24.

[7]郭锋,马震岳,金长宇.抽水蓄能电站地下洞室初始地应力场反演分析——基于神经网络和快速拉格朗日算法[J].地下空间与工程学报,2007,3(2):208－212.GUO Feng,MA Zhen-yue,JIN Chang-yu.Back analysis of initial ground stress of underground cavern of power station——Based on artifical neural network and fast Lagrangian analysis[J].Chinese Journal of Underground Space and Engineering,2007,3(2):208－212.

[8]贾善坡,陈卫忠,谭贤君,等.大岗山水电站地下厂房区初始地应力场Nelder-Mead 优化反演研究[J].岩土力学,2008,29(9):2341－2349.JIA Shan-bo,CHEN Wei-zhong,TAN Xian-jun,et al.Nelder-Mead algorithm for inversion analysis of in-situ stress field of underground powerhouse area of Dagangshan hydropower station[J].Rock and Soil Mechanics,2008,29(9):2341－2349.

[9]王福玉,高谦,张周平.金川矿区地应力规律与人工神经网络预测研究[J].岩石力学与工程学报,2003,22(增刊2):2601－2606.WANG Fu-yu,GAO Qian,ZHANG Zhou-ping.Law of in-situ stress in Jinchuan diggings and research on prediction model based on artifical neural network[J].Chinese Journal of Rock Mechanics and Engineering,2003,22(Supp.2):2601－2606.

[10]张国强,王桂萱.基于神经网络结构分解与FLAC3D的初始地应力场反演[J].大连大学学报,2007,28(6):43－47.ZHANG Guo-qiang,WANG Gui-xuan.Back-analysis of initial ground stress field based on neural network ensemble and generation of the initial ground stress field by using Flac3D[J].Journal of Dalian University,2007,28(6):43－47.

[11]岳晓蕾,李术才,陈启辉,等.多元多方程地应力反演与工程应用研究[J].山东大学学报,2010,40(2):66－77.YUE Xiao-lei,LI Shu-cai,CHEN QI-hui,et al.Inversion of an initial geostress field by the method of multivatiate analysis and the research of engineering application[J].Journal of Shandong University,2010,40(2):66－77.

[12]江权,冯夏庭,徐鼎平,等.基于围岩片帮形迹的宏观地应力估计方法探讨[J].岩土力学,2011,32(5):1452－1459.JIANG Quan,FENG Xia-ting,XU Ding-ping,et al.Evaluation method of general geostress based on spalling features of wall rock[J].Rock and Soil Mechanics,2011,32(5):1452－1459.

[13]云庆夏,黄光球.遗传算法和遗传规划及其在矿业中的应用[J].中国矿业,1997,30(6):62－66.YUN Qing-xia,HUANG Guang-qiu.Genetic alogorithm and genetic programming and their application in mining[J].China Mining Magazine,1997,30(6):62－66.

[14]张明,周永权,王冬冬.一种基于遗传规划的数据拟合方法[J].哈尔滨工程大学学报,2006,27(增刊):527－530.ZHANG Ming,ZHOU Yong-quan,WANG Dong-dong.A data fitting method based on genetic programming[J].Journal of Harbin Engineering University,2006,27(Supp.):527－530.

[15]乔金丽,刘波,李艳艳,等.基于遗传规划的边坡稳定安全系数预测[J].煤炭学报,2010,55(9):1466－1469.QIAO Jin-li,LIU Bo,LI Yan-yan,et al.The prediction of the safety factor of the slope stability based on generic programming[J].Journal of China Coal Society,2010,55(9):1466－1469.

[16]阙金声,陈剑平,王清,等.遗传算法在土坡整体稳定性分析中的应用[J].岩土力学,2008,29(2):415－419.QUE Jin-sheng,CHEN Jian-ping,WANG Qing,et al.Genetic algorithm applied to entire stability analysis of soil slope[J].Rock and Soil Mechanics,2008,29(2):415－419.

[17]汪秉文,范衠,康小海.遗传算法在Matlab环境中的实现[J].武汉汽车工业大学学报,1999,21(6):25－28.WANG Bing-wen,FAN Zhun,KANG Xiao-hai.Realization of genetic algorithm in Matlab[J].Journal of Wuhan Automotive Polytechnic University,1999,21(6):25－28.

[18]翟淑花,高谦.遗传规划在最大下沉值预测中的应用[J].煤炭学报,2007,32(3):239－242.ZHAI Shu-hua,GAO Qian.Application of genetic programming on predicting maximum surface subsidence due to mining[J].Journal of China Coal Society,2007,32(3):239－242.

[19]张金水,闫长斌,邢光辉,等.基于遗传规划的采空区地面沉陷预测分析[J].华北水利水电学院学报,2011,32(4):113－115.ZHANG Jin-shui,YAN Chang-bin,XING Guang-hui,et al.Prediction analysis on the surface subsidence in minedout areas based on genetic programming[J].Journal of North China Institute of Water Conservancy and Hydroelectric Power,2011,32(4):113－115.

[20]王小平,曹立明.遗传算法理论应用与软件实现[M].西安:西安交通大学出版社,2002.

[21]边霞,米良.遗传算法理论及其应用研究进展[J].计算机应用研究,2010,8(7):2425－2429,2434.BIAN Xia,MI Liang.Development on genetic algorithm theory and its applications[J].Application Research of Computers,2010,8(7):2425－2429,2434.