复杂地铁车站施工对邻近建筑物变形影响数值分析的位移叠加法

徐帮树，丁万涛，刘林军，晏 勤，陈 诚

（1.山东大学岩土与结构工程研究中心，济南 250061；2.安徽省建筑科学研究设计院，合肥 230001）

1 引言

近年来，随着城市化进程的不断加快，巨大交通压力已经成为许多大中型城市面临的一个难题，由于地下交通具有较高的输送效率，而且也不影响城市景观，其运行时的噪音、震动等对沿线居民干扰较小，城市地铁建设已经成为一个解决交通压力的有效途径[1－3]。地铁的选线大多穿越城市人口密集区，地铁区间隧道从各种建构筑的下方或者周边通过，而地铁车站基坑的开挖往往不可避免靠近周边建筑，开挖施工无论做出什么样的支护措施，都会不可避免的对周围的围岩造成扰动，浅埋隧道的影响范围更广，对地表的沉降影响更显著，因地铁施工引起的建筑不均匀沉降、倾斜、甚至倒塌的案例不在少数[4－7]。通过数值模拟[8－13]手段，计算地铁施工对周边建筑的影响效果，为设计方案的比选提供依据，是目前应用比较普遍的一种方法。

地铁的建设是一个极为复杂的施工过程，特别是地铁车站的建设，有明挖基坑部分，有与区间隧道对接的暗挖段，常常还有换乘站的联络通道建设，各种空间结构复杂，也造成了对周边建筑的影响因素较多。然而，数值模拟中很难在一个模型中考虑所有的影响因素，计算量大，建模也非常的困难，这成为制约用数值模拟解决复杂地铁车站的障碍之一。

本文根据朱维申等[14]提出的施工过程力学原理，即围岩在进行开挖和支护的过程实际上是在空间和时间上不断变化条件下对其进行反复加载的过程，提出位移叠加法的概念，把复杂地铁车站的模型的建立分为整体模型和局部模型。整体模型考虑基坑开挖主体结构的影响，不考虑细部结构（如暗挖段、联络通道等局部的影响）。局部模型要建立大比例的模型，着重考虑与周边建筑相近或影响现状的细部结构。计算中把整体模型计算得到的位移场作为局部模型的初始位移场，通过局部模型的计算得到了综合基坑主体结构和细部结构对建筑物的影响和位移场。

2 位移叠加法计算思路

朱洪高等[15]将双圆盾构隧道施工引起的地表位移等效为单圆隧道施工的地表位移的叠加。Addenbrooke 等[16]计算前后施工引起地表总沉降的方法是将单个隧道沉降进行叠加，得到总沉降。任强等[17]研究双孔平行隧道施工引起的地表沉降是由2 条隧道单独施工引起的位移之和。朱维申等提出的施工过程力学原理指出，对围岩进行开挖和支护的过程从力学分析实际上是在空间和时间上不断变化条件下对其进行反复加载的过程，首次从力学角度说明了隧道施工过程中开挖和支护都是对围岩施加荷载，即荷载的结果必然是与应力路径相关的。本工程实例中，车站基坑和暗挖段的开挖过程可以理解为2 次加载的过程。在小变形及线弹性范围内，同时承受几种荷载作用时每一种荷载引起的位移将不受其他荷载的影响，可以分别计算各种荷载单独作用下的位移，然后求出它们的代数和既是所有荷载共同作用下的位移。本文提出数值计算位移叠加法，把复杂的地铁基坑工程划分为整体模型和若干局部模型，先计算整体模型车站基坑开挖对邻近建筑物的变形影响，将整体模型计算所得出的位移结果作为局部模型的初始位移场，利用有限差分软件Flac3D进行计算，得出最终的位移结果。

3 节点位移插值方法

3.1 单元内插法

根据有限元基本原理[18]可知，利用局部坐标系的规则形状的单元(母单元)的高阶位移模式的形函数进行位移转换，得到关于整体坐标系的复杂形状的单元(子单元)。

形函数即是单元的任意一点的位移插值函数，满足：

（1）在节点i 处， Ni=1，在其他的节点处， Ni=0。

（2）能保证用它定义的位移在相邻单元之间的连续性。

（3）应包含任意线性项，以保证用它定义的单元位移可满足常应变条件，应满足式（1），以保证用它定义的单元位移能够反映刚体位移。

三维母单元是(ξ0,η0,ζ0)坐标系中的2 × 2 ×2正六面体。如图1 所示。坐标在单元形心上，单元边界是6个平面：ξ=±1,η=±1,ζ=±1 单元节点在角点及各边的等分点上。

三维线性单元的形函数为

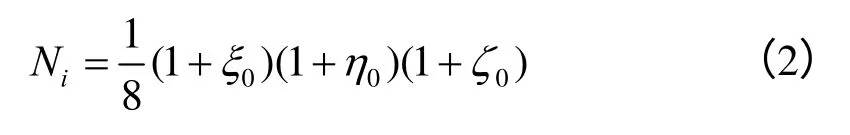
式中：

子单元的位移模式可用形函数表示为

图1 三维线性单元Fig.1 Three-dimensional linear unit

以上位移模型形函数（见式（4））给出了局部坐标系位移和整体坐标系位移之间的一一对应关系，如果给定了局部性坐标系的位移值，就可以求出整体坐标系中对应的位移值，反之亦然。

数值计算中使整体模型和局部模型坐标一一对应，采用Fish 语言编程，搜索待求节点在整体模型中对应实体单元，对该单元8个节点的位移值按单元内插法获取待求节点的初始位移。在此基础上对局部模型初始位移场进行赋值，并进行开挖模拟，得到的叠加位移场即为最终位移场。

3.2 反距离加权插值法[19]

设空间待插点为P(xp,yp,zp)，P 点邻域内有已知散乱点 Qi(xi,yi,zi)，i=1，2，…，n，利用距离加权反比法对P 点的属性值Zp进行插值。其插值原理是待插点的属性值是待插点邻域内已知散乱点属性值的加权平均，权的大小与待插点与邻域内散乱点之间的距离有关，是距离的k(0≤k≤2，k一般取2)次方的倒数，即

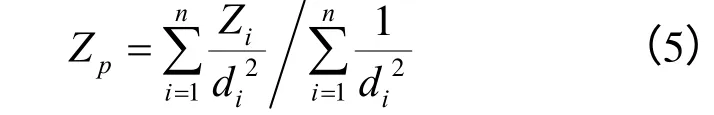
插值函数为

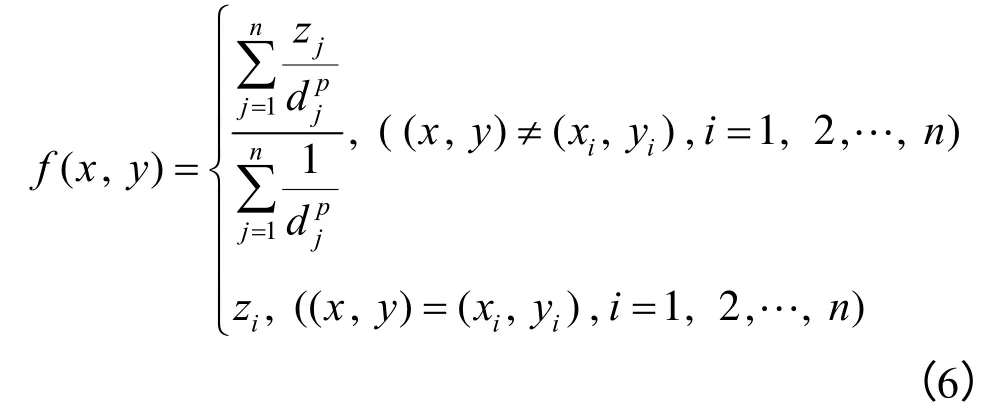
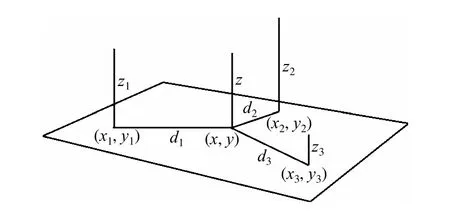
图2 反距离加权插值示意图Fig.2 Sketch of inverse distance weighted interpolation

在整体模型中，以某一半径搜索距离待求节点最近的8～12 节点，假定距离越近节点位移值越接近待求节点，采用反距离加权插值获取待求节点初始位移。

4 工程实例

4.1 潜山路车站工程概况

潜山路车站位于合肥市长江西路和潜山路的交叉口，是轨道交通2号线和3号线的换乘车站。长江西路和潜山路均为城市主干道，因此，潜山路站所处位置交通流量很大。

2号线车站为地下3 层岛式车站，起讫里程为YDK24+282.779～YDK24+507.615。车站主体结构为3 层双柱3 跨钢筋混凝土框架结构，总长224.84 m。车站东西端均设端头井，端头井宽度为25.2 m。2号线车站设有4个出入口及2 组风亭，基坑标准深度约为10 m。车站的主体结构站西侧的暗挖段采用暗挖法施工，车站两侧的区间隧道采用盾构法施工。车站主体结构采用钻孔灌注桩+压密注浆止水帷幕作为其围护结构，车站附属结构拟采用钻孔灌注桩作为其围护结构。

4.2 计算力学参数

研究区域位于糜棱岩断层带，根据潜山路站地质勘查报告，地层取V 级围岩参数，围岩物理力学参数建议值见表1，各支护结构参数见表2、3。计算时将内支撑弹性模量折减80%。

4.3 计算模型

潜山地铁站周边环境复杂，为了提高计算精度和计算效率，数值模型主要分为两部分，即整体模型和局部模型。整体模型主要考虑主体基坑开挖支护过程中对丰乐大厦和丰乐公寓基础变形的影响，在计算过程中不考虑暗挖段施工对基础变形的影响；局部模型主要用于计算车站暗挖段的施工对丰乐大厦和丰乐公寓的变形的影响。先计算整体模型车站基坑开挖对邻近建筑物的变形影响，将整体模型计算所得出的位移结果作为局部模型的初始位移场，利用有限差分软件Flac3D进行计算，得到暗挖段施工后的最终位移结果。

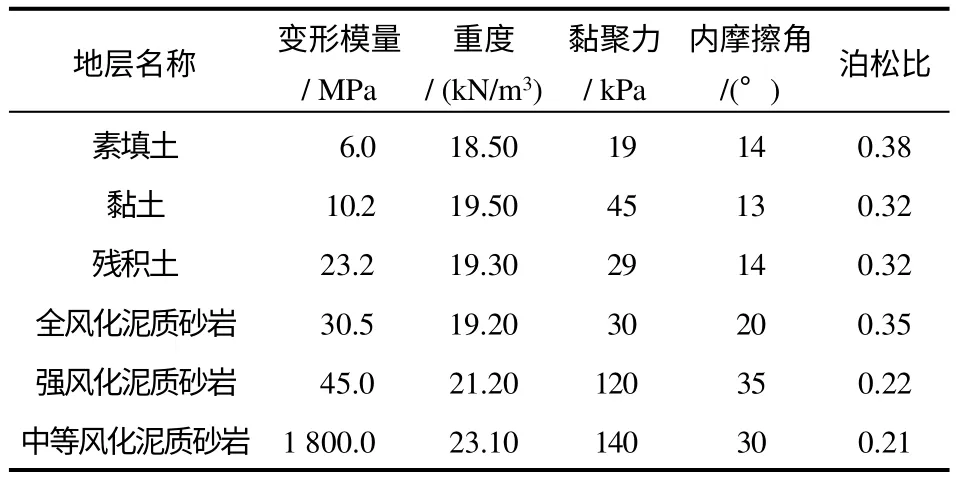
表1 各土层的物理力学参数Table 1 Physico-mechanical parameters of the soil

表2 围护结构参数表Table 2 Mechanical parameters of enclosure structure

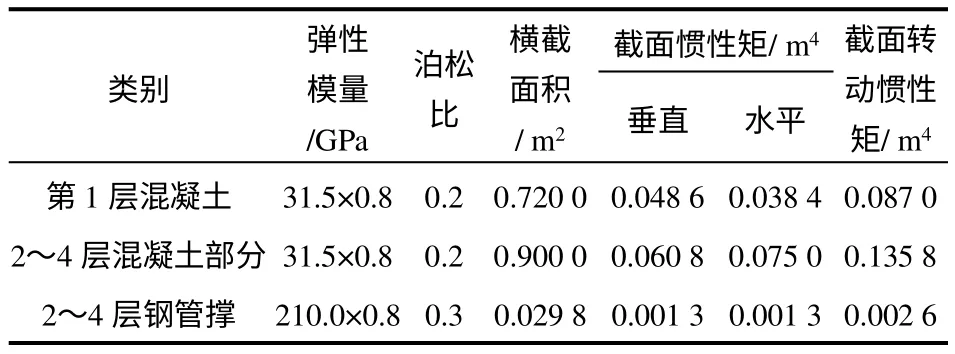
表3 内支撑结构参数Table 3 Mechanical parameters of internal support structure

4.3.1 整体计算模型

潜山站整体计算模型主要考虑基坑开挖对丰乐公寓和丰乐大厦两栋建筑的影响。潜山路站基坑平面长185 m，主体部分宽26 m，基坑最大开挖深度为26.5 m，分8 步开挖。计算模型的三维尺寸为452 m×288 m×106 m。数值计算模型采用有限差分软件FLAC3D进行计算分析，通过ABAQUS 有限元软件辅助建立计算网格模型，导入到FLAC3D中，建立的3D 网格模型如图3 所示。

计算模型四周的外边界约束边界面法向位移，模型底部z=-106 m 采用固定约束，z=0 水平地表为自由表面。土体采用8 节点六面体实体单元模拟。土体结构计算采用Mohr-Coulumb 本构模型。计算选用的物理力学参数参考表1。

计算模型只考虑自重应力，不考虑构造应力，地应力计算平衡后添加上部建筑物荷载，再次平衡后将位移归0，得到基坑整体模型初始应力场。

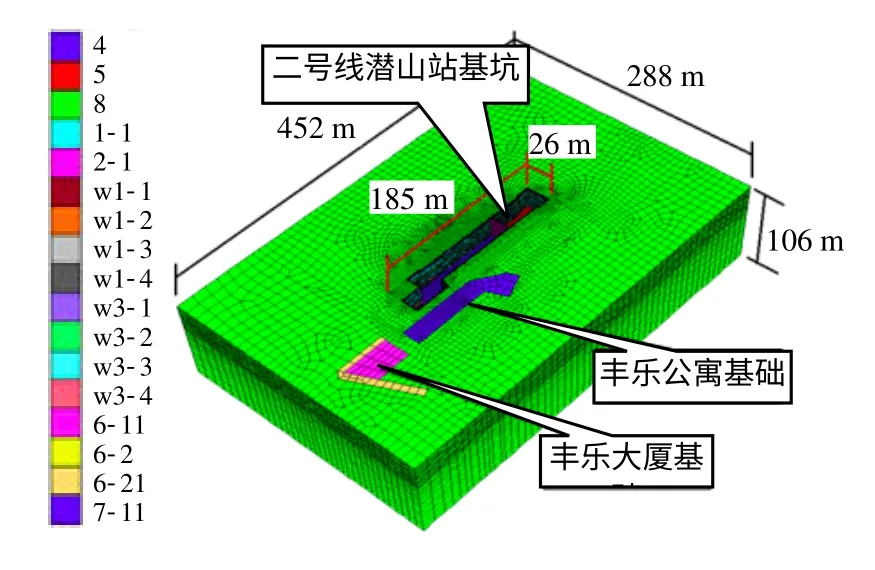
图3 整体计算模型Fig.3 Global calculation model

4.3.2 潜山路站暗挖段局部计算模型

暗挖段隧道结构采用复合式衬砌。初期支护采用钢筋网、系统锚杆、格栅钢架及喷砼联合支护。在此数值模型中，由基坑和隧道开挖引起的地面沉降的影响范围取桩基深度的5 倍，暗挖部分长40 m。因此，计算模型的三维尺寸为133.2 m×189.31 m×67 m。数值计算模型采用有限差分软件FLAC3D进行计算分析，通过ABAQUS 有限元软件辅助建立计算网格模型，导入到FLAC3D中，建立的3D 网格模型如图4 所示。实体单元分组：sd 表示隧道；flgyd表示丰乐公寓地下室；flgyj 表示丰乐公寓基础；fldsd 表示丰乐大厦地下室；tc 表示土层。

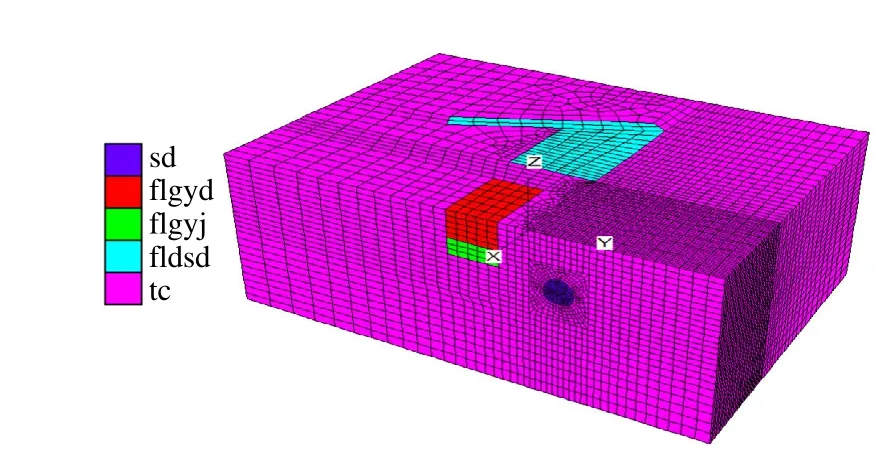
图4 局部计算模型Fig.4 Local calculation model

计算模型四周的外边界约束边界面法向位移，模型底部z=-67 m 采用固定约束，z=0 水平地表为自由表面。土体采用8 节点六面体实体单元模拟。土体结构计算采用Mohr-Coulumb 本构模型。计算选用的物理力学参数见表1。丰乐公寓和丰乐大厦的桩基土壤强度参数采用刚度等效的方法换算得到。

计算模型只考虑自重应力，不考虑构造应力，地应力计算平衡后添加上部建筑物荷载，再次平衡后将位移归0，得到暗挖段局部模型初始应力场。

4.4 计算过程模拟

（1）基坑整体模型开挖过程模拟

①设置土体的初始应力状态和边界条件；

②进行基坑东侧开挖，每步开挖完成后加一层内支撑，共开挖4 步；

③进行基坑西侧开挖，每步开挖完成后加一层内支撑，共开挖4 步。

（2）暗挖段局部模型开挖过程模拟

①设置土体的初始应力状态和边界条件；

②进行隧道开挖，每步开挖2 m，开挖后暂时不进行支护，待下一步开挖完成后再进行衬砌支护；

③重复步骤②，直到开挖完成，共开挖20 步。

4.5 结果分析

（1）采用单元内插法基坑和暗挖段开挖对建筑物的影响分析

丰乐大厦和丰乐公寓最终沉降值主要由基坑开挖造成的沉降和暗挖段施工造成的沉降叠加而得。采用单元内插法计算得到基坑和暗挖段开挖后建筑物的沉降云图，如图5 所示。

图5 建筑物沉降云图（单位：0.1 mm）Fig.5 Nephogram of settlements of buildings(unit:0.1 mm)

由单元内插法计算模拟结果可知，潜山站基坑开挖对评估范围内建构筑物（丰乐公寓和丰乐大厦）造成的沉降变化影响不大，丰乐大厦由基坑开挖和暗挖段开挖共同作用引起的最大沉降值为0.136 mm，最大隆起值为0.072 mm，差异沉降为0.208 mm。丰乐公寓由基坑开挖和暗挖段开挖共同作用引起的最大沉降值为0.154 mm，最大隆起值为0.122 mm，差异沉降为0.276 mm。根据《建筑地基基础设计规范》[20]，均小于建筑物沉降允许值和差异沉降允许值。距离暗挖段越近，建筑物沉降越大，较远一侧则发生隆起。建筑沉降随基坑开挖深度增大而增大，沉降主要受基坑西侧3、4 层施工工况影响较大。

（2）采用反距离加权插值法基坑和暗挖段开挖对建筑物的影响分析

采用反距离加权插值法计算得到基坑和暗挖段开挖后建筑物的沉降云图见图6。

通过反距离加权插值法计算模拟结果可知，潜山站基坑开挖对评估范围内建构筑物（丰乐公寓和丰乐大厦）造成的沉降变化影响不大。丰乐大厦由基坑开挖和暗挖段开挖共同作用引起的最大沉降值为0.101 mm，最大隆起值为0.075 mm，差异沉降为0.176 mm。丰乐公寓由基坑开挖和暗挖段开挖共同作用引起的最大沉降值为0.179 mm，最大隆起值为0.169 mm，差异沉降为0.348 mm。沉降特点与单元内插法得到的结果相似。

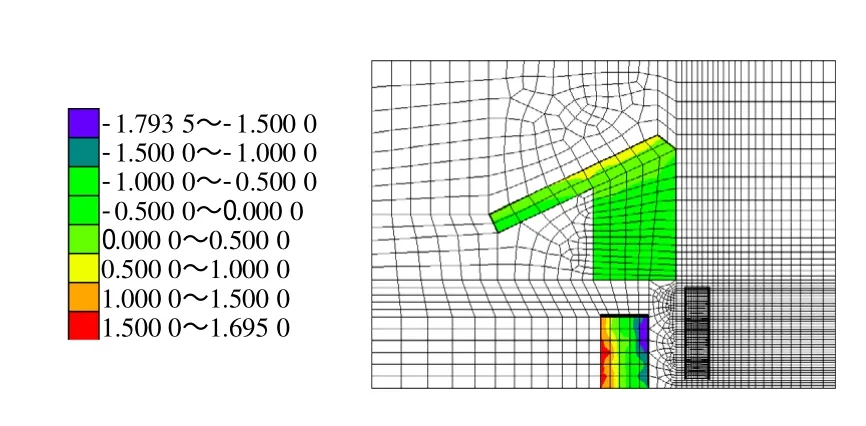
图6 建筑物沉降云图（单位：0.1 mm）Fig.6 Nephogram of settlements of buildings(unit:0.1 mm)

（3）单元内插法和反距离加权插值法计算结果对比分析

将整体模型和局部模型进行单独开挖模拟计算，分别得到基坑开挖和暗挖段施工对建筑物的沉降影响，将两种结果进行叠加结果见表4、5。

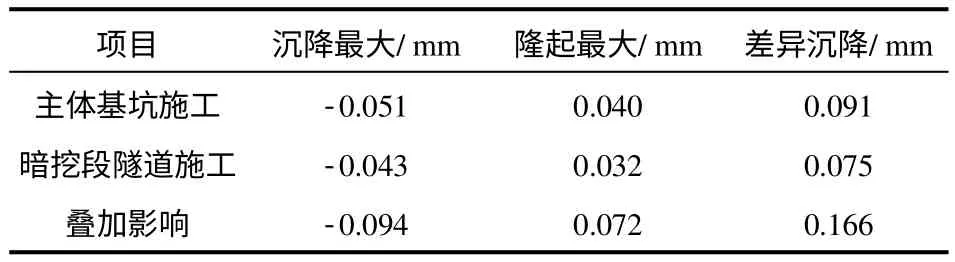
表4 丰乐大厦沉降影响综合评价Table 4 Comprehensive settlement evaluation of Fengle building

表5 丰乐公寓沉降影响综合评价Table 5 Comprehensive settlement evaluation of Fengle apartment

通过单元内插法和反距离加权插值法计算得到的结果见表6、7。

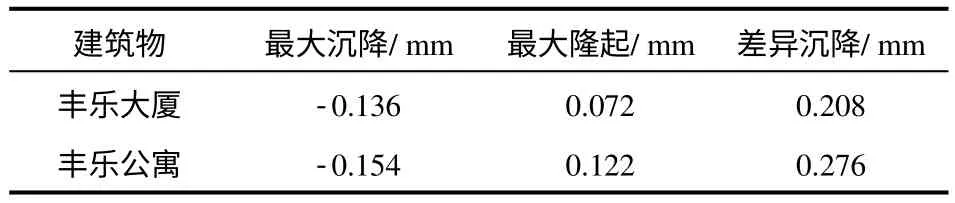
表6 单元内插法计算结果Table 6 Calculation results by elementary interpolation method

将上述两种方法得到的建筑物沉降与两种模型单独计算得到的沉降结果进行比较。由以上结果可知，整体模型和局部模型单独计算得到的建筑物位移峰值与采用反距离加权插值法计算得到的结果相差不到0.005 mm，与采用单元内插法计算得到的结果相差不到0.05 mm。由此可知，采用位移叠加法得到的计算结果与单独计算结果非常接近。为方便计算，位移叠加法是可行的。并且采用反距离加权插值法比单元内插法具有更高的计算精度。

5 结论

（1）采用Fish 语言编程，搜索局部模型中待求节点在整体模型中对应坐标附近8～12个节点。导出首先计算得到的整体模型位移场，作为局部模型的初始位移场，再对局部模型进行开挖计算，通过位移叠加法得到的位移场可近似作为完整模型计算结果。

（2）通过位移叠加法对复杂地铁车站进行数值模拟计算时，采用反距离加权插值法比单元内插法具有更高的精度，得到的计算结果更准确。

[1]钱七虎.迎接我国城市地下空间开发高潮[J].岩土工程学报,1998,20(1):112－113.QIAN Qi-hu.Meet the exploitation climax of underground space in China[J].Chinese Journal of Geotechnical Engineering,1998,20(1):112－113.

[2]钱七虎.岩土工程的第四次浪潮[J].地下空间,1999,19(4):267－272.QIAN Qi-hu.The fourth wave of geotechnology[J].Underground Space,1999,19(4):267－272.

[3]关宝树,国兆林.隧道及地下工程[M].成都：西南交通大学出版社,2000.

[4]赵衍发.浅埋暗挖法下穿既有地铁车站的风险控制[D].北京:北京交通大学,2013.

[5]徐庆辉.地铁浅埋暗挖隧道塌方事故原因分析及建议[J].土工基础,2012,26(4):31－33.XU Qing-hui.Collapse and remediation of shallow buried tunnel during construction[J].Soil Engineering And Foundation,2012,26(4):31－33.

[6]邓小鹏,李启明,周志鹏.地铁施工安全事故规律性的统计分析[J].统计与决策,2010,26(9):87－89.DENG Xiao-peng,LI Qi-ming,ZHOU Zhi-peng.Subway construction accidents regular statistical analysis[J].Statistics and Decision,2010,26(9):87－89.

[7]韩守信,张青松.新奥法隧道施工塌方原因事故树分析[J].能源与环境,2009,28(5):104－108.HAN Shou-xin,ZHANG Qing-song.The new Austrian law tunnel construction cause collapse accident analysis[J].Energy and Environment,2009,28(5):104－108.

[8]麻凤海,张维来,吕培印.地铁车站深基坑开挖对土体影响的数值模拟[J].辽宁工程技术大学学报(自然科学版),2012,31(3):295－299.MA Feng-hai,ZHANG Wei-lai,LU˙˙Pei-yin.Numerical simulation on effect of soil deformation caused by excavating deep foundation pit of subway station[J].Journal of Liaoning Technical University(Natural Science),2012,31(3):295－299.

[9]姜忻良,宗金辉,孙良涛.天津某深基坑工程施工监测及数值模拟分析[J].土木工程学报.2007,40(2):79-84.JIANG Xin-liang,ZONG Jin-hui,SUN Liang-tao.Construction monitoring and numerical simulation for a deep excavation in Tianjin[J].China Civil Engineering Journal,2007,40(2):79－84.

[10]赵延林,高全臣,衡朝阳.基坑开挖对近邻建筑物沉降影响的数值模拟[J].黑龙江科技学院学报,2005,15(2):106－110.ZHAO Yan-lin,GAO Quan-chen,HENG Chao-yang.Numerical analysis of effects about sedimentation deformation of nearby building created by excavation of foundation pit[J].Journal of Heilongjiang Institute of Science&Technology,2005,15(2):106－110.

[11]ZHOU N Q,VERMEER P A,LOU R X,et al.Numerical simulation of deep foundation pit dewatering and optimization of controlling land subsidence[J].Engineering Geology,2010,114(3－4):251－260.

[12]王善勇,唐春安,王述红,等.地铁开挖对地基沉降影响的数值分析[J].东北大学学报(自然科学版),2002,23(9):887－890.WANG Shan-yong,TANG Chun-an,WANG Shu-hong,et al.Numerical simulation and research of the influence on the excavation of the subway to the bade sedimentation[J].Journal of Northeastern University(Natural Science),2002,23(9):887－890.

[13]FENG S L,WU Y H,LI J,et al.The analysis of spatial effect of deep foundation pit in soft soil areas[J].Procedia Earth and Planetary Science,2012(5):309－313.

[14]朱维申,李术才,白世伟,等.施工过程力学原理的若干发展和工程实例分析[J].岩石力学与工程学报,2003,22(10):1586－1591.ZHU Wei-shen,LI Shu-cai,BAI Shi-wei,et al.Some developments of principles for construction process mechanics and some case history studies[J].Chinese Journal of Rock Mechanics and Engineering,2003,22(10):1586－1591.

[15]朱洪高,郑宜枫,陈昊.双圆盾构隧道土体地表沉降特性[J].建筑科学与工程学报,2006,23(2):62－67.ZHU Hong-gao,ZHENG Yi-feng,CHEN Hao.Characteristics of soil surface settlement for double-O-tube shield tunnel[J].Journal of Architecture and Civil Engineering,2006,23(2):62－67.

[16]ADDENBROOKE T I,POTTS D M.Twin tunnel interaction:Surface and subsurface effects[J].The International Journal of Geomechanics,2001,1(2):249－271.

[17]任强,杨春英,徐薇.地表沉降的双洞体叠加Peck 公式及数值分析[J].安徽理工大学学报,2013,33(4):78－82.REN Qiang,YANG Chun-ying,XU Wei.The Peck formula and numerical analysis of surface subsidence caused by tunnel excavation[J].Journal of Anhui University of Science and Technology(Natural Science),2013,33(4):78－82.

[18]颜云辉.结构分析中的有限单元法及其应用[M].沈阳:东北大学出版社,2000.

[19]靳国栋,刘衍聪,牛文杰.距离加权反比插值法和克里金插值法的比较[J].长春工业大学学报,2003,24(3):53－57.JIN Guo-dong,LIU Yan-cong,NIU Wen-jie.Comparison between inverse distance weighting method and kriging[J].Journal of Changchun University of Technology,2003,24(3):53－57.

[20]中华人民共和国住房和城乡建设部.GB50007－2011建筑地基基础设计规范[S].北京:中国建筑工业出版社,2011.