一道竞赛题的巧解妙法
2014-02-13方芳徐汪华
方芳徐汪华
(1程集中学 安徽宿松246521;2安庆师范学院化学化工学院 安徽安庆246011)
题目(第23届国际奥林匹克化学竞赛预备题有机化学第16题):在沥青的气体中,存有稠环芳烃,其中一些可视为萘(A)、芘(B)和蒽并蒽(C)的同系物,同样原子增加还可以有D、E等等。
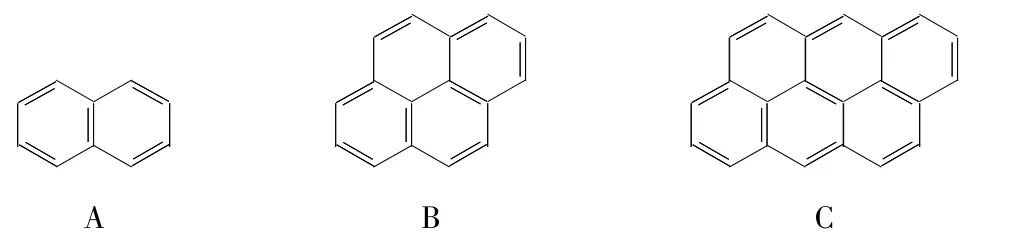
①试推测该系列化合物中,碳的最大含量?
②A+H2可能有多少个产物生成?它们之中哪个是热力学最稳定的?
③设氢化反应在相邻的位置上进行,试推测B+2H2的反应中,哪个产物是最稳定的?
解析:本题虽是20世纪国际奥林匹克化学竞赛预备题,但至今依然是考察学生观察能力和分析能力的一道好题。要推测该系列化合物中碳的最大含量,必须先求出该系列化合物的分子式通式。由结构式求通式这类题型的一般解法是:先根据结构式写出分子式,再用等差数列法求出通式。这种方法的第一步稍不注意就会把分子式弄错,分子式一错则后面全错。这种方法的第二步受数学基础的制约,若数学基础不好就难以用等差数列法求出通式。在实际教学中,若尝试用“加减法”来解此类题则简便快捷,答案准确。
(1)第一步:求“最小重复单元”。把该系列中任意相邻两项的后一项减去前一项得“最小重复单元 ”(将前一项平移与后一项部分重叠,再将重叠部分去掉后,剩余部分即表1中各项示意式中的涂黑部分),即C6H2(1、2、3、4、5、6号位各有1个C共6个C,1、6号位各有1个H共2个H。除位于边界的“最小重复单元”外,其余“最小重复单元”的2、3、5号位上均没有H;所有“最小重复单元”的4号位上均没有H)。
第二步:求“主体”。该系列中第1项有1个“最小重复单元”(表1中第1项示意式中涂黑部分,下同);第2项有2个“最小重复单元”;第3项有3个“最小重复单元”;……;第n项有n个“最小重复单元”,即第n项的主体为“(C6H2)n”。
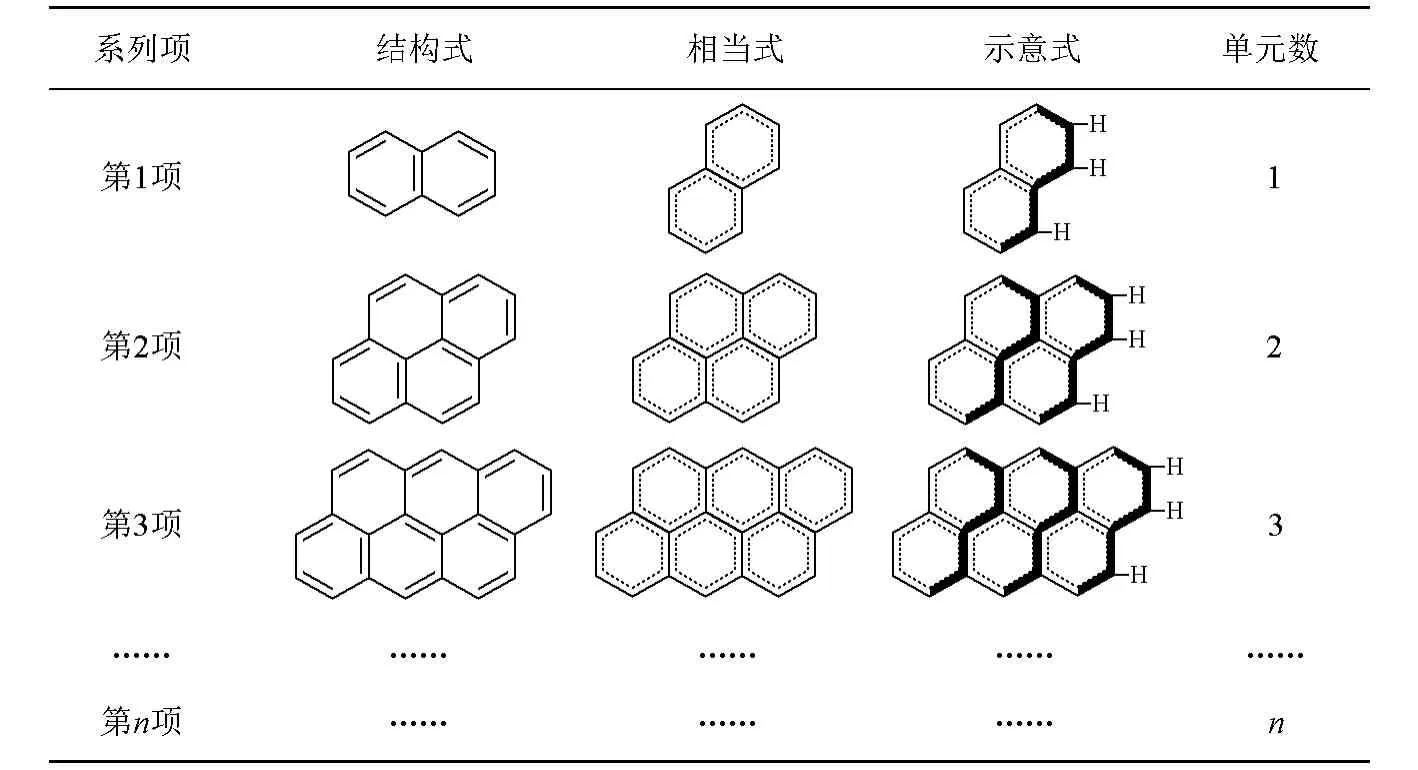
表1 题目求解示意图
第四步:写“通式”。第n项的“左边”+“主体”+“右边”=“通式”,即C4H3+(C6H2)n+H3=C6n+4H2n+6。
第五步:求碳的最大含量。该系列化合物中,碳的含量(质量分数)为:
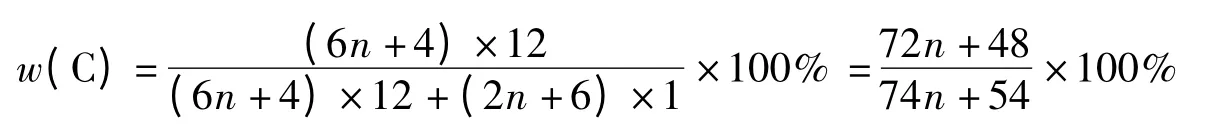
当n→∞时,碳的最大含量为:
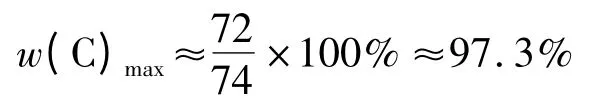
(2)萘分子()为平面结构,有两条处于分子平面内的C2轴a、b。处于对称位置的氢原子等价,所以萘分子中的氢原子可分为两组:1、4、5、8位置的4个氢原子等效为一组;2、3、6、7位置的4个氢原子等效为一组。
1mol萘与1mol H2发生加成反应时,生成的“1,2加成产物”为(1,2)(表示两个H加到1和2号位置所得到的产物,以下类同)、(2,3)、(1,9)、(9,10),它们的结构式分别为生成的“1,4加成产物”为(1,4)、(1,7)、(2,10),它们的结构式分别为生成的“1,6加成产物”为(1,5)、(2,6),它们的结构式分别为其中,1,2-二氢化萘中含有苯环且苯环与双键形成一个共轭体系,在所有生成物中其热力学稳定性最高。
(3)当氢化反应在相邻的位置上进行时,B+2H2的反应可以生成很多产物,其中最稳定的产物是
练习(1998年高考化学测试题第21题):下面是苯和一组稠环芳香烃的结构式:

(1)写出化合物②~⑤的分子式:①C6H6,②________,③________,④________,⑤________。
(2)这组化合物的分子式通式是C________H________(请以含n的表示式填在横线上,n=1,2,3,4,5,…)。
(3)由于取代基的位置不同,产生的异构现象称为官能团位置异构。一氯并五苯有________(填数字)个异构体;二氯蒽有________(填数字)个异构体。
答案:(1)C10H8,C14H10,C18H12,C22H14。(2)4n+2,2n+4。(3)4,15。提示:“最小重复单元”为,即C4H2(1、2、3、4号位各有1个C,共4个C;1、4号位各有1个H,共2个H。除位于边界的“最小重复单元”外,其余“最小重复单元”的2、3号位上均没有H);“左边”为,即C2H2(5、6号位均有1个C和1个H,共2个C和2个H;1、4号位的C和H在“最小重复单元”中已经记数,不能重复计算);“主体”为(C4H2)n;“右边”为2个H(写作H2)(2、3号位各有1个H,这2个H并不包括在位于边界的“最小重复单元”中);“通式”为C2H2+(C4H2)n+H2=C4n+2H2n+4。
像求“通式”这类型的题目,用“减法”找出“最小重复单元”后即可直接用“加法”写“左边”+“主体”+“右边”=“通式”,快速高效。用“加减法”和“编号法”不仅提高了解题速度和解答的正确性,更重要的是能提高学生分析问题和解决问题的能力,开发学生的智力。
[1]南京大学化学系有机化学教研室编.有机化学(上册).北京:高等教育出版社,1984
[2]邢其毅,徐瑞秋,周政.基础有机化学(上、下册).北京:高等教育出版社,1987
