直流侧故障下MMC-HVDC输电线路过电压计算

潘武略，裘愉涛，张哲任，宣羿，徐政

(1.浙江省电力公司，杭州市310007;2.浙江大学电气工程学院，杭州市310027)

0 引言

随着电力电子技术的发展，模块化多电平换流器(modular multi-level converter，MMC)极大地促进了高压直流(high voltage direct current，HVDC)输电技术的发展。2001年MMC首次被提出之后，凭借其高品质的输出波形以及较低的功率损耗，在学术界和工业界引起了研究者的兴趣，在拓扑结构、数学建模、协调控制、故障保护等方面已经研究得较为透彻［1-7］。作为电压源型换流器(voltage source converter，VSC)的一种，MMC在兼具VSC所有优势的同时，还具有器件一致触发动态均压要求低、扩展性好、开关频率低以及运行损耗低等诸多优势［8-10］。目前，基于模块化多电平换流器的高压直流(modular multi-level converter-high voltage direct current，MMC-HVDC)输电系统已广泛应用于风电、太阳能等新能源并网的场合，目前已有上海南汇直流输电示范工程、浙江舟山多端柔性直流输电示范工程、广东南澳多端柔性直流输电示范工程等投入运行或正在建设中。MMCHVDC输电技术也可以应用于改善城市配电的场合，如位于旧金山的Transbay Cable工程、厦门跨海柔性直流输电重大科技示范工程等。对于海岛供电等特殊应用场合，MMC-HVDC输电技术也有其独特的优势。可以预见，在未来电力系统的构成中，MMCHVDC输电技术将会成为其必不可少的组成部分。

在MMC-HVDC线路工程中，电缆占据了建设成本中相当大的一部分。目前普遍认为，直流侧单极接地故障会对MMC-HVDC线路直流电缆产生严重的影响［11］。因此，该故障下直流电缆上的电压应力是主回路参数设计的重要依据。然而由于换流器结构的不同，MMC-HVDC线路与二电平VSC-HVDC线路直流侧故障的特性并不相同，针对二电平VSC-HVDC线路的结论也就不能适用于MMC-HVDC线路。因此有必要对MMC-HVDC线路直流侧单极接地故障下过电压特性进行细致的分析，并且筛选出有效的计算方法。

本文首先介绍MMC的基本运行特性，以此作为后续分析的理论基础;随后，针对MMC-HVDC线路直流侧最有可能发生的单极接地故障和双极短路故障，分别描述了其故障特性;然后，基于直流侧单极接地故障，详细分析了3种可用来计算健全极过电压的模型;最后，基于电磁暂态仿真软件PSCAD/EMTDC，搭建了400 MW/±200 kV数字仿真平台，验证了2种等效模型的有效性。

1 MMC的基本结构

MMC的基本结构如图1所示，每个换流器由3个相单元组成，每个相单元分为上、下2个结构对称的桥臂。

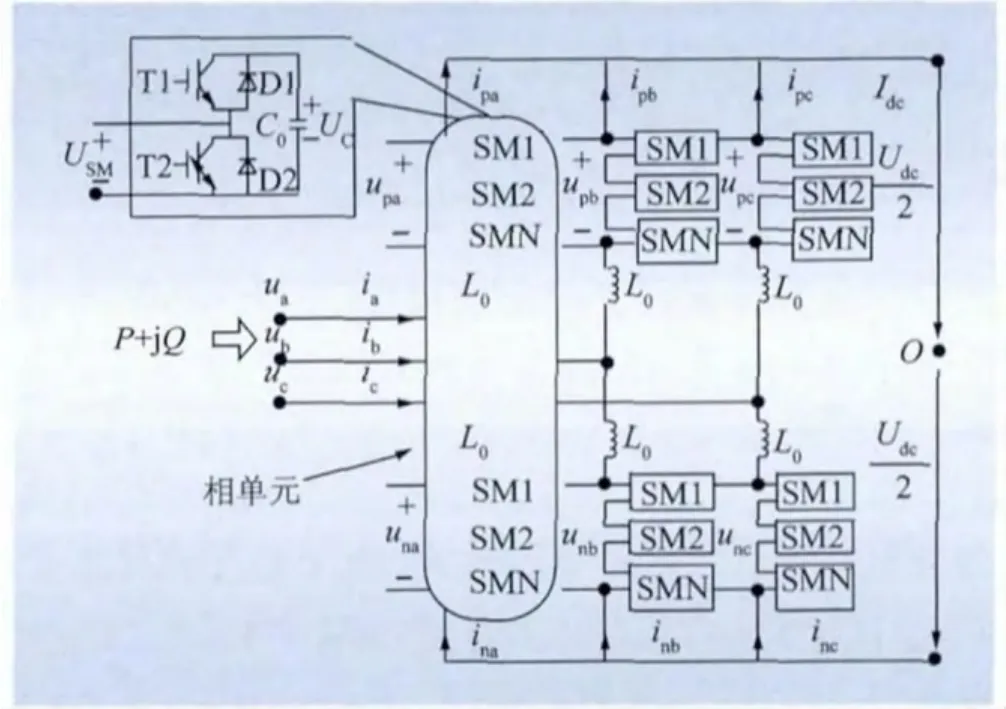
图1 MMC的基本结构Fig.1 Basic structure of MMC

由图1可知:每个桥臂都由N个串联的子模块以及桥臂电感L0组成。每个子模块由2个绝缘栅双极型晶体管(T1、T2)、2个反向并联二极管(D1、D2)以及子模块电容C0构成，子模块电容额定电压为UC0，子模块电容电压为UC，子模块输出电压为USM。

在稳态运行方式下，根据能量守恒原理，换流器交、直流侧的电压、电流存在以下关系［12］:

式中:P、Q分别为注入MMC的有功功率和无功功率;φ为功率因数角;Pdc为换流器的直流输出功率;U为换流器交流侧线电压的有效值;Udc为换流器正负极之间的直流电压;I为换流器交流侧线电流有效值;Idc为换流器输出的直流电流;ipk、ink、ik和 icirck分别为k相上桥臂电流、下桥臂电流、交流电流以及环流，其中 k 取 a，b，c。

从直流侧看，为了维持输出的直流电压恒定，必须要求3个并联的相单元处于投入状态的子模块数目相等且不变，并且满足以下关系［13］:

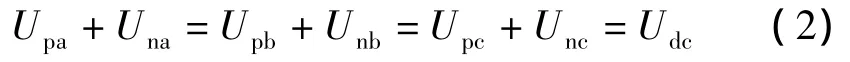
式中:Upk和 Unk分别为 k(k=a，b，c)相上桥臂电压和k相下桥臂电压。又因为相单元中处于投入状态的子模块数是一个不变的量，所以在一般情况下，每个相单元中处于投入状态的子模块数为N个，是相单元全部子模块数(2N)的1/2。

2 MMC-HVDC线路直流侧故障分析

目前绝大部分的MMC-HVDC工程都采用电缆作为输电线路，且把电缆深埋于海底或地底，直接降低了直流故障的概率。然而人为的挖断或者船锚拖断，会导致直流侧故障的发生，而且往往是永久性故障，因此在检测到故障之后，会先闭锁换流器，随后切除故障线路所连接的换流站。目前分析双极短路故障的文献较多，而分析单极接地故障的论文则较少。为避免累赘，本文只粗略介绍双极短路故障;对于单极接地故障，则进行较为详细的分析计算。

2.1 双极短路故障

目前普遍认为，双极短路故障是MMC-HVDC系统中最严重的故障类型［14-15］。通过仿真分析可以发现，故障电流由直流分量和交流分量构成，其中直流分量占主导地位。故障电流的直流分量源于子模块电容的放电过程:子模块闭锁之前，子模块电容通过子模块上部的绝缘栅双极型晶体管(insulated gate bipolar transistor，IGBT)(图1 中 T1)进行放电，放电回路可以近似等效为1个RLC回路，故障电流会迅速上升到相当大的数值。故障电流的交流分量源于交流电网的短路电流，从交流侧看过去，相当于发生了三相短路故障。无论从子模块电流经受的电流应力还是从交流电网的安全稳定性来说，双极短路故障的影响比其他故障严重得多。

2.2 单极接地故障

目前的MMC-HVDC输电线路多采用伪双极结构，如图2所示，接地装置为这2种接地方式的直流系统提供了电位参考点［16］。

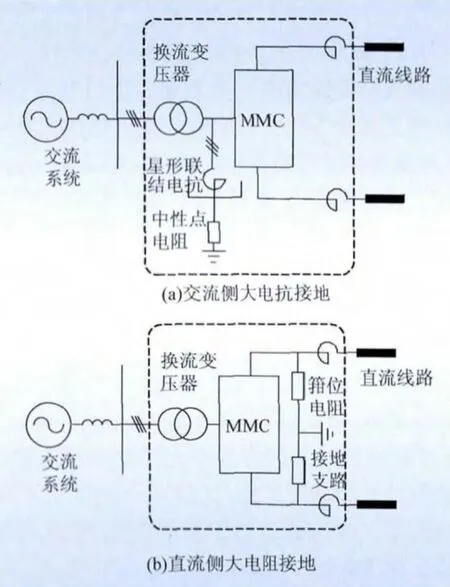
图2 伪双极结构MMC-HVDC的2种接地方式Fig.2 Two grounding modes for MMC-HVDC with pseudo-bipolar structure

为了减小接地装置上消耗的有功功率和无功功率，一般在系统主回路参数设计中，会选取较大的接地电抗和接地电阻。因此在直流侧单极接地故障发生时，故障电流几乎不从这个高阻抗的接地回路通过。在单极接地故障下，整个换流站(不包括换流变压器的一次侧)以及直流线路会出现一定分量的直流偏置，特别是直流线路，其暂时过电压会达到额定电压的2倍左右。必须对换流站以及直流线路的绝缘水平进行合理设计。

3 单极接地故障下MMC-HVDC输电线路过电压的计算模型

从过电压计算的角度分析，多端MMC-HVDC与两端MMC-HVDC输电系统并无本质上的区别。为了简化分析过程，本文以两端MMC-HVDC系统为例，分析比较了几种可用于计算MMC-HVDC系统在单极接地故障下健全极直流线路过电压的模型，分别为:基于电磁暂态仿真平台所搭建的详细模型，基于电磁暂态仿真平台所搭建的等效模型I以及可用解析法计算的等效模型II。

3.1 详细模型

详细模型需要在电磁暂态平台下搭建，换流站必须包含详细的换流器(如图1所示)和控制器，同时电缆也必须采用软件中自带的输电线路模型(比如PSCAD中采用的是频率相关模型)。这种基于电磁暂态平台下搭建详细模型的数字仿真方法精度最高，但是需要耗费大量的时间和计算机资源，如果需要计算的工况较多，该方案就不是最好的选择。

3.2 等效模型I

如上文所述，直接采用详细模型计算会消耗大量的仿真计算时间。为了提高计算效率，提出了一种MMC平均值模型［17］，作为MMC详细模型的简化。该模型将MMC分解为交流侧等效模型和直流侧等效模型。对于交流侧，MMC满足公式(3)和(4):

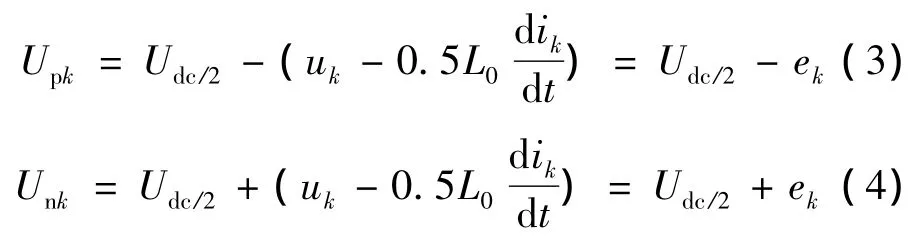
对于直流侧，平均值模型的推导基于能量守恒定律。对于有功功率而言，MMC直流侧输出有功功率等于交流侧输入功率减去MMC中损耗的有功功率。定义调制比如公式(5)所示，则有功功率守恒可表示为公式(6)和公式(7)的形式:

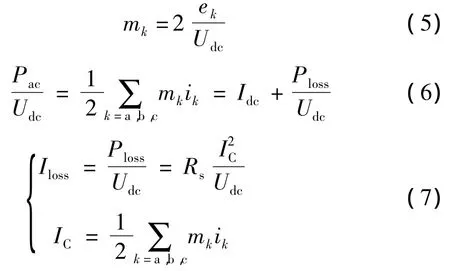
式中:Ploss为换流器上的功率损耗，Rs为MMC等效电阻，mk(k=a，b，c)为k相调制比。其他符号定义如上文所示。

综合公式(3)～(7)，可以得到MMC平均值模型如图3所示。需要指出的是，除了2个电流源以外，简化模型I直流侧还有1个等效电容，它的大小可以通过公式(8)来确定。

若发生了直流侧单极接地故障，在MMC闭锁之后，MMC可以等效为1个三相6脉动换流器，因此，上述模型在闭锁后需要将等效电容切除，且把直流出口之前的晶闸管触发导通，以体现直流电流的单向流动性。

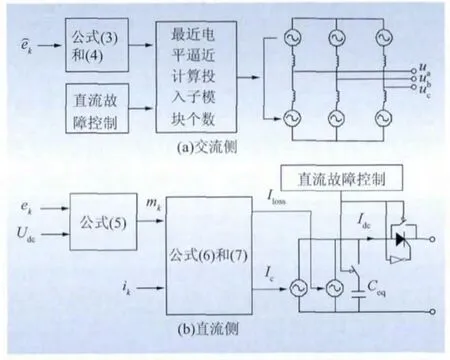
图3 MMC平均值模型示意图Fig.3 Average value model of MMC

需要指出，上述模型只能较为精确地模拟闭锁之前健全极直流线路的电压变化特性。在所考虑的单极接地故障下，直流线路的过电压最大值通常出现在换流器闭锁之前，因此认为上述简化模型计算的直流线路过电压水平是有效的。

3.3 等效模型II

上述简化虽然能够极大地提高计算效率，但是由于它使用了控制器以及直流线路模型，因此计算过程依旧离不开电磁暂态仿真平台。有必要提出一种能够脱离电磁暂态仿真软件的，适用于计算单极接地故障下直流线路过电压的等效模型。

如2.2节内容所述，在单极接地故障下，较大的接地回路阻抗直接导致了较小的故障电流，从而能基本维持电容电压大小不变。考虑到MMC闭锁前，每个相单元每一时刻都有N个子模块投入运行，因此这些串联的子模块可以被等效成大小等于Udc的理想电压源。

由于闭锁前直流电流在3个相单元中平均分配，因此可以将MMC等效为1个Udc理想电压源和1个大小为2/3L0(L0如图1所定义)电感的串联。如果再考虑了MMC直流出口的平波电抗器(假设其大小为L1)，换流站就可以等效为Udc(电压源)、2/3L0(电感)和2L1(电感)的串联。为了简化后面的分析过程，将串联的2/3L0(电感)和2L1(电感)使用等效电感Ls代替。

对于直流电缆的健全极，可以使用Matlab中的Power_Cableparam命令计算其单位长度电感、单位长度电阻以及单位长度电容。之后利用所得的电缆参数计算其Π等效电路。对于故障极，可以假设整条线路为理想接地。

假设发生了直流线路正极接地故障，那么故障后瞬间的等效电路如图4所示，其中:C2、R2和L2分别为直流海缆Π等效电路的等效电阻、电感和电容;Udc为额定直流电压;Rs1(Rs2)和Ls1(Ls2)分别为换流站1(换流站2)的等效电阻和等效电感。

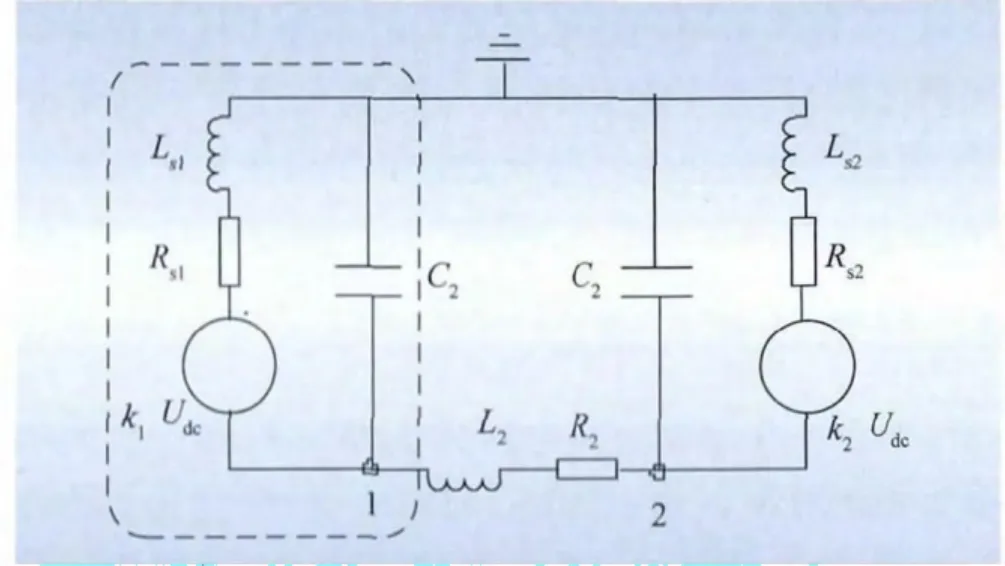
图4 MMC简化模型II示意图Fig.4 Simplified model II of MMC

正常运行状态下，2个换流站的直流电压或多或少与额定直流电压有一定偏差，图4中采用比例系数k1和k2来描述这种偏差。需要重点关注点1和点2的电压变化情况。

下面使用拉普拉斯变换来计算输电线路首末端的电压变化情况。通过推导，可以得到拉普拉斯变换之后节点1和2的节点电压方程为

显然通过求解这个方程，就可以得到复频域上节点电压［U1，U2］T，再经过拉普拉斯反变换，就能求解出其时域表达式。

特别地，当2个换流站的等效电感大小相等时，考虑到换流站等效电阻很小，对过电压计算结果影响不大，并且2个换流站稳态运行直流电压几乎等于额定直流电压，经过简化，可以发现直流线路首末端节点电压［U1(t)，U2(t)］T大小相等，都作周期等于的震荡衰减:

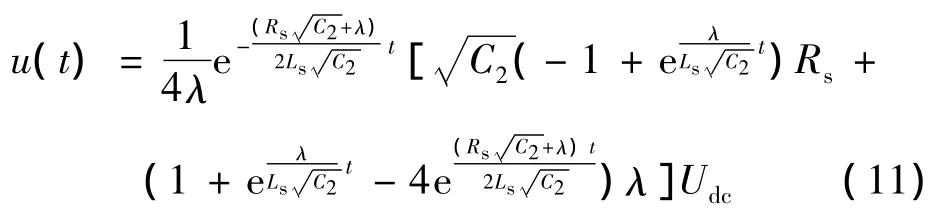
式中:Rs(Rs1，Rs2)和 Ls(Ls1，Ls2)为换流站等效电感和等效电阻，Cs(C1，C2)是直流海缆Π等效电路的等效电容显然，根据对称性原则，也能发现公式(10)实际上描述的是图4中虚线中电容C2的电压。

与简化模型I类似，该模型也只能计算故障后闭锁前直流线路首末端过电压情况。然而在单极接地故障下，直流线路的过电压最大值通常出现在换流器闭锁之前，且整条直流线路上的最大过电压几乎相等，因此该模型也可以高效地计算单极接地时直流线路的过电压。

4 计算结果分析

对于一个额定直流电压为±200 kV，额定直流功率为400 MW的两端MMC-HVDC系统，使用3种计算模型，分别计算单极接地故障下健全极电缆的过电压水平。MMC-HVDC系统主回路参数如表1所示，其中直流电缆单位长度的电气参数通过Matlab中的Power_Cableparam命令求得。

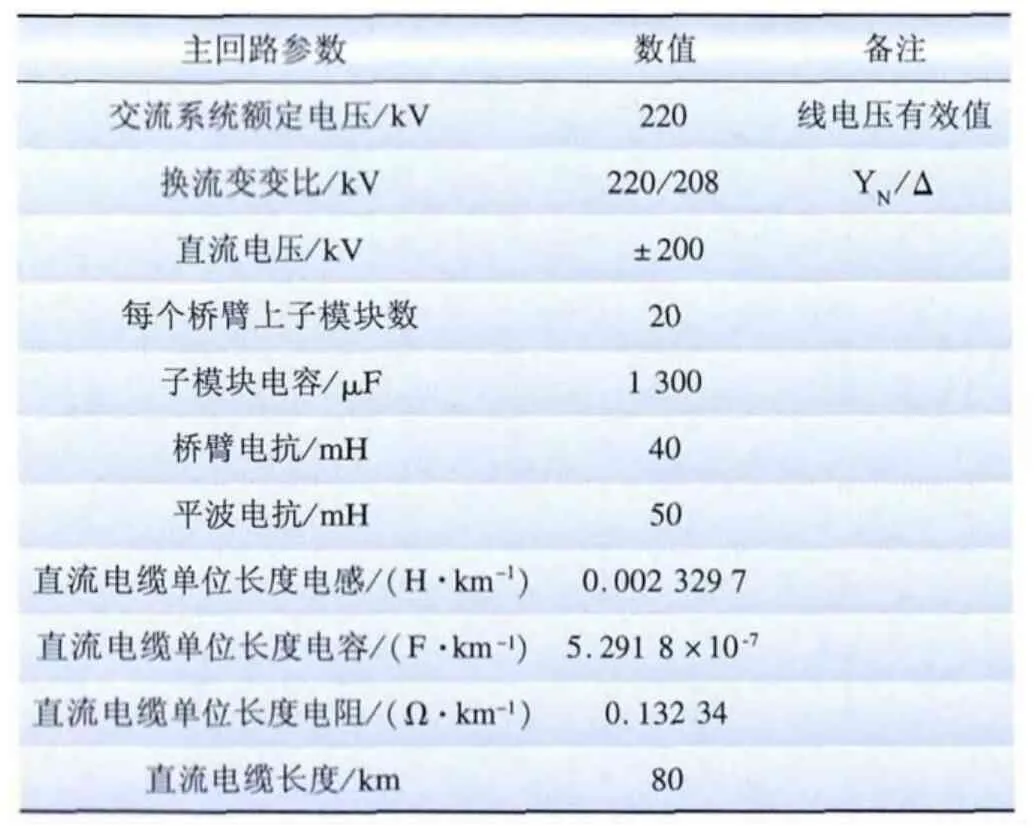
表1 仿真系统主回路参数Tab.1 Main circuit parameters of simulation system

假设在1 s时发生了正极线路单相接地故障，故障5 ms之后换流器闭锁，故障100 ms之后交流断路器断开。首先使用基于PSCAD/EMTDC软件搭建的数字仿真平台计算过电压波形，作为后续2种简化模型有效性验证的依据。仿真所得的故障后健全极的过电压波形如图5所示。

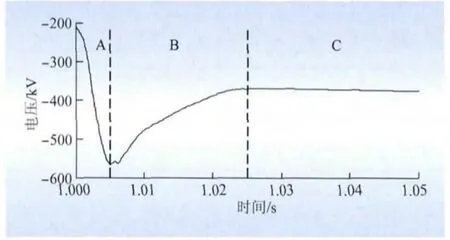
图5 健全极过电压波形Fig.5 Overvoltage waveform simulated by detailed model

由图5可知:交流断路器断开之前，健全极的电压变化分为3个阶段，如图5的A、B、C所示。阶段A:RLC回路充放电过程，在这个过程中，电缆电容的初始电压为－200 kV，围绕－400 kV作振荡衰减，其最大值能达到570 kV左右，略小于初始电压的3倍。

闭锁后的阶段C则对应于MMC变成3相六脉动桥的直流输出电压波形。阶段B位于2个阶段之间，几乎是一个单调的衰减过程。在详细模型的仿真结果中还可以发现，单极接地故障下健全极的最大过电压出现在换流器闭锁之前。因此使用等效模型I、II来计算直流电缆最大过电压是可行的。

图6给出了故障后、闭锁前3种模型所得到的直流电缆健全极过电压波形结果。

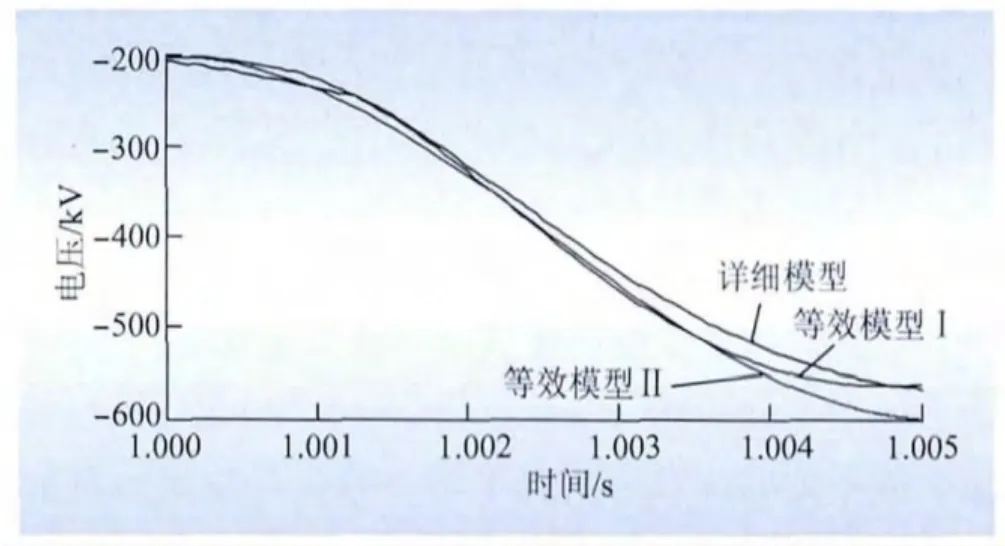
图6 闭锁前3种模型的健全极过电压波形对比Fig.6 Comparison of overvoltage waveform before blocking in 3 models

由图6可知:2种等效模型的计算结果与详细模型的计算结果差别不大，各有优势。若观察最大过电压的计算结果，等效模型I的结果更为精确;然而从振荡周期以及过电压波形变化趋势来看，等效模型II的结果更接近详细模型的结果。在提高了计算效率的同时，2种等效模型都有较高的精确性。

5 结论

为了快速而有效地完成MMC-HVDC直流侧单极接地故障下健全极最大过电压的计算，本文详细分析了3种可能的计算模型。详细模型必须在时域仿真平台下搭建，其精度最高，但是需要耗费大量计算时间;基于能量守恒定律，能够得到等效模型I;结合拉普拉斯变换与电路分析原理，能够得到等效模型II。基于测试系统，分别使用3种模型计算其直流侧单极接地故障下健全极最大过电压;对比计算结果，发现2个等效模型的计算结果都有较高的精度。

［1］管敏渊，徐政.模块化多电平换流器型直流输电的建模与控制［J］.电力系统自动化，2010，34(19):64-68.

［2］管敏渊，徐政.MMC型VSC-HVDC系统电容电压的优化平衡控制［J］.中国电机工程学报，2011，31(12):9-14.

［3］李笑倩，宋强，刘文华，等.采用载波移相调制的模块化多电平换流器电容电压平衡控制［J］.中国电机工程学报，2012，32(9):49-55.

［4］赵昕，赵成勇，李广凯，等.采用载波移相技术的模块化多电平换流器电容电压平衡控制［J］.中国电机工程学报，2011，31(21):48-55.

［5］丁冠军，丁明，汤广福，等.新型多电平VSC子模块电容参数与均压策略［J］.中国电机工程学报，2009，29(30):1-6.

［6］屠卿瑞，徐政，管敏渊，等.模块化多电平换流器环流抑制控制器设计［J］.电力系统自动化，2010，34(18):57-61.

［7］赵成勇，陈晓芳，曹春刚，等.模块化多电平换流器HVDC直流侧故障控制保护策略［J］.电力系统自动化，2011，35(23):82-87.

［8］韦延方，卫志农，孙国强，等.适用于电压源换流器型高压直流输电的模块化多电平换流器最新研究进展［J］.高电压技术，2012，38(5):1243-1252.

［9］屠卿瑞，徐政.基于结温反馈方法的模块化多电平换流器型高压直流输电阀损耗评估［J］.高电压技术，2012，38(6):1506-1512.

［10］刘钟淇，宋强，刘文华.基于模块化多电平变流器的轻型直流输电系统［J］.电力系统自动化，2010，34(2):53-58.

［11］仉雪娜，赵成勇，庞辉，等.基于MMC的多端直流输电系统直流侧故障控制保护策略［J］.电力系统自动化，2013，37(15):140-145.

［12］Ilves K，Antonopoulos A，Norrga S，et al.Steady-state analysis of interaction between harmonic components of arm and line quantities of modular multi-level converters［J］.IEEE Transactions on Power Electronics，2012，27(1):57-68.

［13］徐政.柔性直流输电系统［M］.北京:机械工业出版社，2013:27-52.

［14］王姗姗，周孝信，汤广福，等.新模块化多电平换流器 HVDC直流双极短路子模块过电流分析［J］.中国电机工程学报，2011，31(1):1-7.

［15］Tu Q，Xu Z，Huang H，et al.Parameter design principle of the arm inductor in modular multi-level converter based HVDC［C］//2010 International Conference on Power System Technology.Hangzhou，China:IEEE，2010:1-6.

［16］徐政，唐庚，黄弘扬，等.消解多直流馈入问题的两种新技术［J］.南方电网技术，2013，7(1):6-14.

［17］Saad H，Peralta J，Dennetière S，et al.Dynamic averaged and simplied models for MMC-Based HVDC transmission systems［J］.IEEE Transactions on Power Delivery，2013，28(3):1723-1730.