基于有限元的模块化多电平换流器绝缘结构分析

张军，吴金龙，梁云丹，陈小军，姚为正

(1.西安许继电力电子技术有限公司，西安市710075;2.国家电网运营监测(控)中心，北京市100031;3.国家电网公司运行分公司，北京市100052)

0 引言

随着光伏发电、风能发电等可再生能源利用规模的不断扩大，其固有的分散性、小型性、远离负荷中心等特点，使得采用交流输电技术或传统的直流输电技术联网很不经济［1］。随着电力电子器件和控制技术的发展，产生了一种新型的直流输电技术，称之为柔性直流输电系统或轻型直流输电系统，这是一种基于电压源型换流器的直流(voltage-sourced converter highvoltage direct current，VSC-HVDC)输电技术，与基于自然换相技术的电流源型换流器的传统直流输电不同，VSC-HVDC输电技术采用了可控关断器件和以脉宽调制(PWM 技术)为基础［2-6］。

换流阀作为核心部件一直是研究的重点，也是换流站设计中最重要的任务。VSC-HVDC换流阀的设计应用了电力电子技术、光控转换技术、高电压技术、控制技术、均压技术、冷却技术和高压用绝缘材料等最新技术和研究成果［7-8］。

在柔性直流输电系统中，MMC作为核心设备在运行中处于高电压大电流的工作状态。高电压绝缘技术是换流阀中比较突出的问题，从本质上来说绝缘结构的绝缘强度就是其承担电场强度的能力［9-10］。

作为一个高电压大功率的电气设备，换流阀的绝缘结构对于设备的安全运行非常重要。在换流阀的绝缘结构中分别采用了固体绝缘和空气绝缘，由于空气的绝缘强度远小于固体绝缘介质，实际运行或试验中电晕、击穿放电、爬电等绝缘故障都是由于其局部的电场超过空气的击穿场强的临界值引起的［11-14］，因此换流阀的电场分析对于绝缘结构设计是非常必要的。由于空气间隙结构和带电体的形状比较复杂，采用估算方法可能导致较大的误差，采用有限元法可以得到比较准确的电场计算结果。

本文以±320 kV模块化多电平电压源换流阀作为研究对象，采用有限元分析方法来计算换流阀的电场分布。对换流阀内部层间、阀塔对地等位置空气间隙的电场进行计算，分析换流阀内部空气间隙的绝缘强度;对换流阀外表面的电场分布进行计算，以研究换流阀外侧是否会发生绝缘故障以及通过计算研究屏蔽罩的性能;通过对换流阀之间空气绝缘强度的分析，研究模块化多电平换流站阀厅的布局。

1 换流阀电场计算模型分析

MMC作为柔性直流输电的核心设备，运行于高电压、大电流条件下。对应的是该设备处于强电场和强磁场的运行环境中，其高压绝缘问题是最突出的问题之一。在换流阀的实际应用中采用空间绝缘和固体介质绝缘。从本质上讲，通过电场强度、电场分布均匀程度等可以分析和判断其绝缘结构的绝缘性能。

在实际的三维空间中，电场的定解条件为

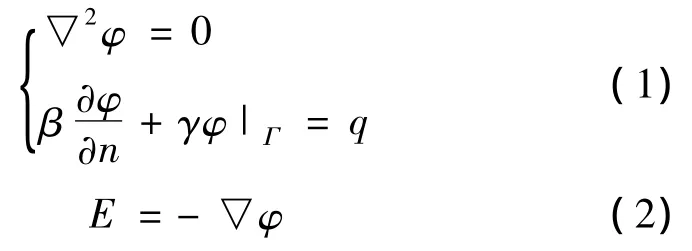
式(1)中:β为0时，为第一类边界条件;γ为0时，为第二类边界条件;β和γ都不为0时，为第三类边界条件。具体边界条件设置要根据计算模型的实际情况来进行分析和判断。

由式(2)可以判断出:电场是电位梯度，在电位变化比较剧烈的位置电场值很大。在换流阀中，金属部件都是高电位，因此其附近的空气间隙中电场分布会比较集中。

实际中子模块都是封装好的，同时模块的外壳都是铁质材料，模块内部的电磁特性不会影响到外部。因此在建立模型时，将子模块等效为一个整体。阀塔的总宽为3 200 mm，长为4 500 mm，阀塔距地面高为3 700 mm。

根据电场计算的方法建立换流阀的有限元模型，如图1所示。

图1 模块化多电平柔性直流输电换流阀有限元模型Fig.1 Finite element model of MMC

根据实际中阀厅尺寸建立换流阀的求解域，其中阀塔底部的对地支撑绝缘子连接地面与阀塔。阀塔的求解域如图2所示。

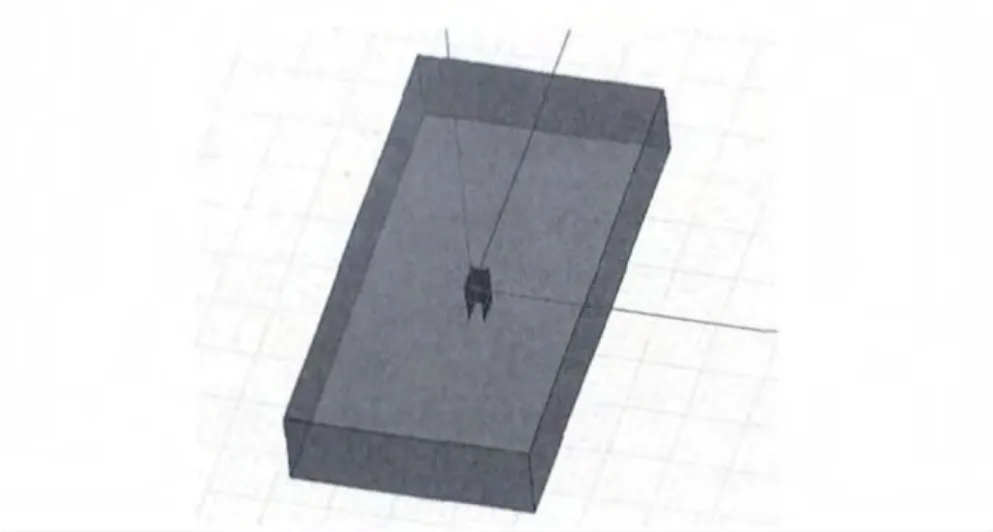
图2 阀塔的求解域Fig.2 Solving region of MMC

阀厅的顶部、地面以及四周墙壁都接地，都属于0电位。根据公式(1)可知:在计算电场时边界条件为第一类边界条件。

2 换流阀内部空气绝缘强度分析

按照实际工况中最极端的情况进行阀塔绝缘结构分析，子模块的最大电压为2.6 kV，实际阀塔运行中如果超过该值，子模块将进行保护动作。

为了研究阀塔内部空气间隙的绝缘强度，对阀塔中局部位置的电场进行分析。经过计算，得到阀塔顶部，空气间隙中最大电场的位置如图3所示。

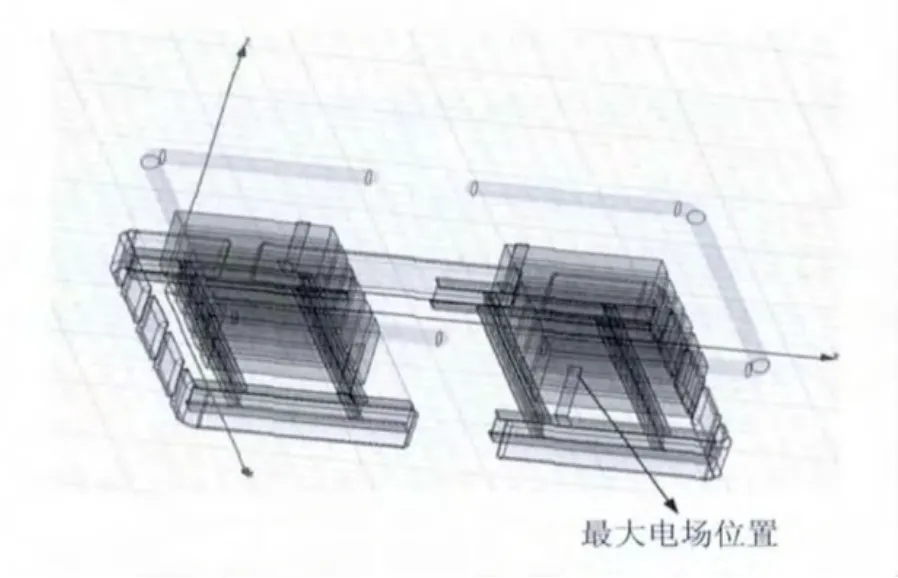
图3 换流阀顶部空气间隙中最大电场位置Fig.3 Maximum electric field strength in the top air gap of MMC

组件端部金属横梁相连的电流铜排和均压环之间的电压差最大，最高可为12个子模块两端的电压值之和，即31.2 kV;而铜排和均压环之间的最小空气间隙距离为199.5 mm。最大电场强度出现在出线端电流母排的顶部位置，由于顶部均压环的屏蔽作用以及母排自身也采取了圆角的设计，因此在该点处最大电场也只有1.13 kV/mm，该值小于空气的临界场强。

阀塔顶部均压环和顶部子模块之间的空气间隙中，电场强度较大。经过计算得到阀塔顶部子模块和均压环之间的电场分布如图4所示。

图4 阀塔顶部和均压环之间空气间隙中的电场分布Fig.4 Electric field distribution in air gap between valve top and grading ring

由图4可以看出:由于均压环的作用，电场比较大的区域集中到了阀塔外侧，最大电场为0.25 kV/mm;在阀塔和均压环内部的电场是非常均匀的，最大电场值为0.08 kV/mm，最小电场值为0.016 kV/mm。在阀塔顶部电场强度比较小，而且电场分布也均匀，因此该位置处的空气绝缘性能较好，可以保证进线端和均压环之间的空气不会发生放电现象。子模块和控制单元等都会处于比较稳定的电场环境中。

在阀塔中层间绝缘子起着支撑上下组件的作用，除了对机械强度有一定要求外，电气性能也很重要。层间绝缘子的高度就是换流阀层间空气间隙的高度。本文中上下组件之间的距离为850 mm，绝缘子两端最大电位差是12个子模块的电压，最大可以达到31.2 kV。层间空气间隙和绝缘子附近空气间隙中的电场分布如图5所示。

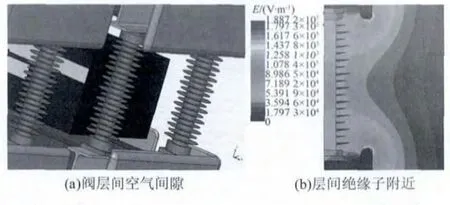
图5 阀层间空气间隙和层间绝缘子附近的电场分布Fig.5 Electric field distribution in air gap or around insulator

屏蔽罩和金属横梁是等电位，上下屏蔽罩之间的最小距离为685 mm，最大电场出现在屏蔽罩的顶点处，最大电场值也只有0.2 kV/mm，远小于空气中电场的击穿场强。由于屏蔽罩对电场分布具有改善作用，因此金属横梁尖角处的电场分布比较均匀。

通过电场计算可以得出:阀塔层间空气间隙的绝缘强度可以满足工程需求。

3 换流阀外部空气绝缘强度分析

MMC采用了支撑式结构，如图1所示，本文中阀塔和地面的之间的距离为3 700 mm。阀塔与地面之间空气绝缘强度的分析是非常重要的。在MMC的绝缘型式试验中，对支撑结构的耐压试验是进行阀塔支撑绝缘子设计的关键步骤。在分析换流阀外部对地空气绝缘强度时，按照绝缘型式试验的条件进行计算。试验中采用的是标准雷电波形1.2/50 μs，电压峰值为1 175 kV。

雷电冲击试验条件下，换流阀对地的最大电场分布如图6所示。

由图6可知:在雷电冲击电压作用下，换流阀和地面之间最大的电场为1.8 kV/mm，该值已经非常接近空气击穿场强的临界值，最大电场的值在屏蔽罩下端位置处。金属横梁上的对地电压为1 175 kV，金属横梁上尖角处是电场比较集中的位置，容易发生尖端放电或者爬电等现象，屏蔽罩的结构改善了金属横梁附近的电场分布。

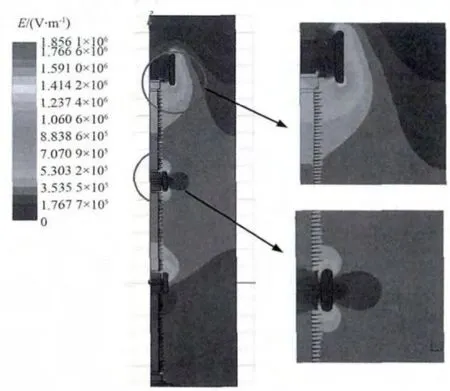
图6 雷电冲击电压作用下支撑绝缘子附件空气间隙的电场分布Fig.6 Electric field distribution in air gap around support insulator under lighting impulse voltage

在2个支撑绝缘子连接处有一定的空气间隙，在雷电冲击下，这些很细微的空气间隙中有可能承担比较大的电场强度，采用均压罩的设计后，电场强度就集中到了均压罩的外侧，如图6所示。

由上述结果可以判断在换流阀试验和运行的过程中，阀塔和地面之间的空气间隙中不会发生放电等绝缘故障。

换流阀运行时，阀塔表面的空气中存在强电场。空气的击穿特性受到电场分布影响，在均匀电场和极不均匀电场中空气起始放电电压差距很大。

通过阀塔外表面上的电场分布来分析阀塔外表面空气绝缘强度。

阀塔x方向外表面和y方向外表面电场分布如图7所示。

图7 阀塔外表面电场分布Fig.7 Electric field distribution on valve surface

由图7可知:在阀塔x方向上的外表面电场分布比较均匀，最大电场和最小电场相差不到4倍，最大电场的位置在阀塔顶部均压环外侧，其中最大电场值为0.74 kV/mm。在y方向一侧表面上的电场分布也非常均匀，电场较大的位置主要在端部屏蔽罩的拐角处，其中最大电场值为0.4 kV/mm。由于屏蔽罩的应用，改善了金属部件尖角处的电场，同时阀塔外侧电场分布均匀，电场强度比较小。

4 阀塔之间空气绝缘强度分析

阀厅中相邻的阀塔之间也存在着比较大的电位差，阀塔之间空气间隙的电场强度是由2个阀塔共同决定。相邻阀塔存在2种情况:同一桥臂的阀塔和相邻桥臂的阀塔。

阀厅中的布局如图8所示。

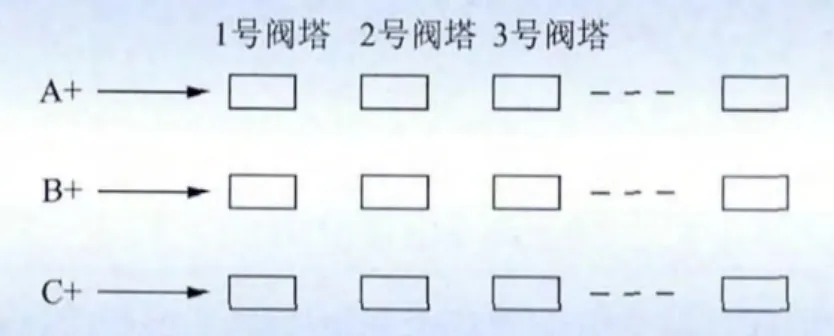
图8 阀厅中阀塔的位置示意图Fig.8 Location of valve tower in hall

针对上述2种情况，分别通过电压的变化分析阀塔之间空气间隙的绝缘强度。

A+和B+进线端1号阀塔之间中心连线上的电场强度变化如图9所示。

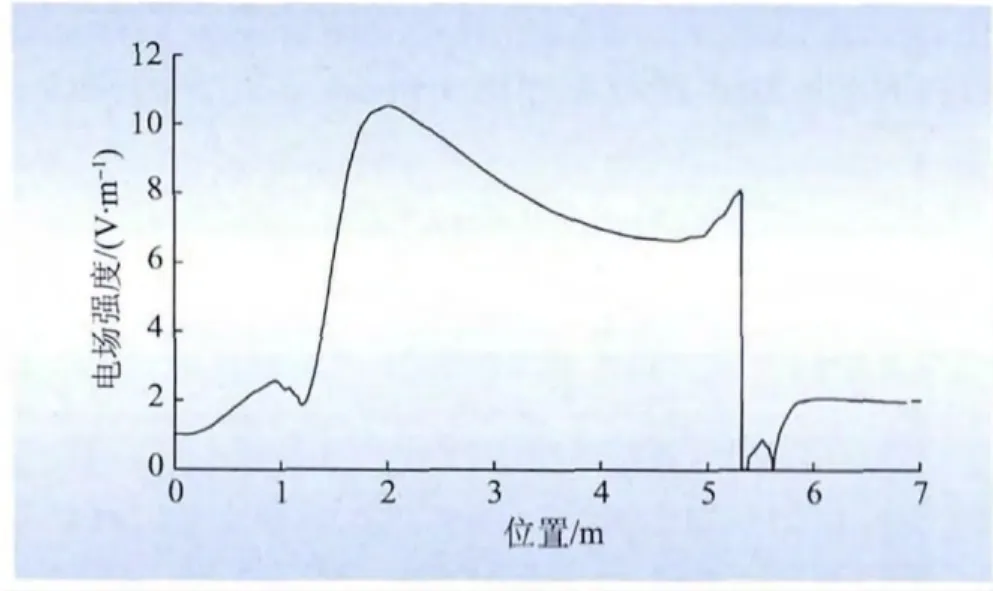
图9 A+和B+进线端1号阀塔之间的电场变化趋势Fig.9 Change trend of electric field strength between A+and B+terminals in No.1 valve tower

A+和B+相邻桥臂中1号阀塔之间的空气间隙承担的电压可以近似等效为阀侧线电压值即344 kV，而这 2个阀塔之间的空气净距离为3 700 mm。图9中:1.5～5.2 m的距离为阀塔之间的空气间隙，阀塔之间的电场强度在距离A+阀塔中心2 m左右的地方达到最大电场强度，即0.105 kV/mm。桥臂间电压最大时A+和B+阀塔对地电位符号相反，因此在空气间隙中电场互相加强，阀塔之间的电场值均在0.06 kV/mm以上。

A+进线端1号阀塔和2号阀塔之间中心连线上的电场强度变化如图10所示。

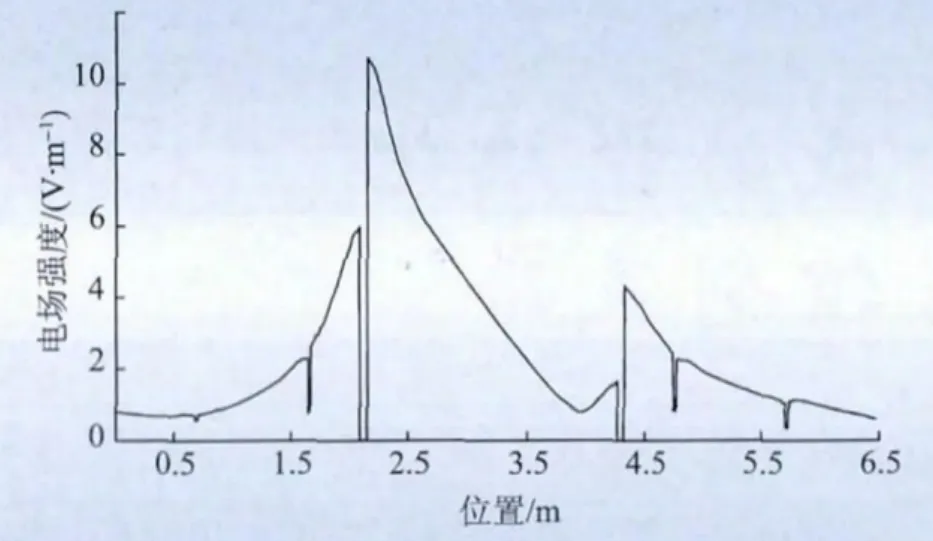
图10 A+进线端1号和2号阀塔之间电场变化趋势Fig.10 Change trend of electric field strength between No.1 and No.2 valve towers with A+terminal

在图10中，1号和2号阀塔外侧的空气净距离为2 000 mm，空气间隙中承担的电压差最大约为78 kV。在1号阀塔屏蔽罩外表面位置即图10中2.2 m位置附近，达到最大电场强度，即0.107 kV/mm。2.2～4.2 m的距离为阀塔之间的空气间隙，同一桥臂的电压相位相同，因此在空气间隙中电场具有相互减弱下降的趋势。

5 结论

在本文分析的模块化多电平柔性直流输电换流阀的绝缘强度中，层间空气绝缘、阀塔对地空气绝缘、换流阀外表面的空气介质中承担的电场强度都能满足换流阀安全运行的要求。由于采用了屏蔽结构，换流阀外表面的电场分布比较均匀。

换流阀层间空气间隙的绝缘强度决定于子模块运行中的最大电压值，采用子模块过压保护电压最大值来进行绝缘性能评估和绝缘结构设计。由于采用了支撑结构，换流阀对地空气间隙中的绝缘强度比较关键。极端情况下电场可以比较合理地分析阀塔对地空气间隙的绝缘强度，并在此基础上指导阀塔支撑结构的设计。通过阀塔之间空气间隙中电场计算，为阀厅的布局提供了参考。

［1］汤广福.基于电压源换流器的高压直流输电技术［M］.北京:中国电力出版社，2009:2-10.

［2］吴亚楠，吕天光，汤广福，等.模块化多电平VSC-HVDC换流阀的运行试验方法［J］.中国电机工程学报，2012，32(30):8-14.

［3］黄俊，赵成勇，高永强.MMC-HVDC换流站过电压与绝缘配合研究［J］.东北电力大学学报，2013，40(1):1-6.

［4］Flourentzou N，Agelidis V G，Demetriades G D.VSC based HVDC power transmission systems:an overview［J］.IEEE Transactions on Power Electronics，2009，24(3):592-602.

［5］Baran M，EI-Markaby I.Fault analysis on distribution feeders with distributed generators［J］.IEEE Transactions on Power Systems，2005，20(4):1757-1604.

［6］Hagiwara M，Akagi H.Control and experiment of pulse widthmodulated modular multilevel converters［J］.IEEE Transactions on Power Electronics，2009，24(7):1737-1749.

［7］严璋.高电压绝缘技术［M］.北京:中国电力出版社，2010:1-15.

［8］马西奎.电磁场理论及其应用［M］.西安:西安交通大学出版社，2002:30-50.

［9］Zhang J，Wang S H，Qiu J.Finite element analysis and evaluation of stator insulation in high voltage synchronous motor［J］.IEEE Transactions on Magnetic，2012，48(2):955-958.

［10］李晓鹏.高压换流阀的绝缘试验设计研究［D］.广州:华南理工大学，2010.

［11］李晓鹏.HVDC换流阀系统屏蔽罩的电场分析和电容参数提取［D］.北京:华北电力大学，2009.

［12］Zhang J，Xu W J，Wang S H.Analysis of inter-turn insulation of high voltage electrical machine by using multi-conductor transmission line model［J］.IEEE Transactions on Magnetic，2013，49(5):1905-1908.

［13］刘士利，魏晓光，曹均正，等.应用混合权函数边界元法的特高压换流阀屏蔽罩表面电场计算［J］.中国电机工程学报，2013，33(25):180-186.

［14］张凌，杨金根，曾静.特高压阀厅电气设计研究［J］.电力建设，2007，28(5):12-16.