冰灾下考虑多种拓扑特性的电网风险分析

黄山，刘俊勇，胥威汀，刘友波，高红均，张放

(1.四川大学电气信息学院，成都市610065;2.智能电网四川省重点实验室，成都市610065;3.四川省电力公司经济技术研究院，成都市610061)

0 引言

拓扑结构不合理是电网恶性事故的重要原因之一。结构的不合理性，将导致电网难以抵御极端灾害［1］。以2008年冰灾为例，我国遭受的持续冰灾，导致全国损失用电量260亿kW·h左右，电网多次发生倒杆断线、跳闸断电及大面积停电事故［2］。冰灾下的电网事故体现出了电网拓扑上的诸多问题，这对电网的拓扑规划带来了更大的挑战。

为了应对以上问题，国内外学者进行了相应的理论研究。文献［3-4］基于复杂网络理论，提出了介数、度数等拓扑特性指标，分别以系统全局效能、连通性为量度，提出了分析电网结构脆弱性的方法。文献［5］量化了充裕性、安全性风险指标，提出了纳入风险指标的电网设计框架。文献［6］定义了长程连接线路，提出了恶劣天气下对连锁故障的预警方法。但是，文献［3-4］缺乏对结构脆弱性的风险分析，并且拓扑特性指标缺乏对网络全局特征的描述。文献［5］虽然纳入了风险因素，但未考虑极端天气可能带来的严重后果。文献［6］忽略了元件故障率随气象指标的变化规律，难以准确地描述某种灾害天气的具体影响。

为解决以上问题，本文旨在研究冰灾下拓扑特性对电网风险的影响，为电网规划提供指导。提出了考虑气象条件和灾害持续时间的冰灾风险指标、全局性的拓扑特性指标，以评估不同结构电网的冰灾风险大小，分析拓扑特性对电网风险的影响。最后以IEEE30节点网络及改进网络为算例，验证了结论的有效性。

1 评估拓扑特性对电网风险影响的思路

本文旨在研究拓扑特性对电网风险的影响，研究冰雪灾害下的电网风险。研究基本思路分为以下4个关键步骤，如图1所示。

步骤1:建立冰灾风险指标。通过建立冰灾下线路故障率模型，进行优化失负荷计算，从而有效地反映冰雪灾害下电网承受的风险大小。

步骤2:提出全局性拓扑特性指标，以描述具有不同拓扑特性的电网结构特征。

步骤3:计算不同拓扑结构的冰灾风险指标，并比较它们的大小。

步骤4:分析拓扑特性的影响。探索拓扑特性与冰灾风险的内在联系，分析具有何种拓扑特性的电网抵御冰灾能力更强。

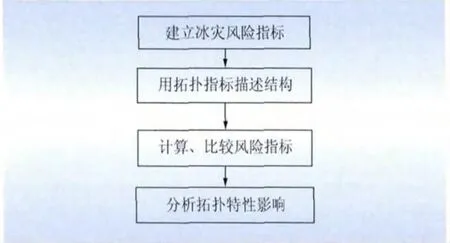
图1 拓扑特性对电网风险影响分析的基本思路Fig.1 Analysis of topological characteristics’inflcence on power system risk

本文所提方法与传统方法不同之处主要有2点:(1)所提拓扑指标从全局性的角度描述整个网络特征;(2)风险指标结合了故障诱因的气象因子，能够更客观、具体地描述某一种灾害带来的风险。

2 建立冰灾风险指标的理论依据

2.1 冰灾线路故障率模型

与传统的冰灾气象模型不同之处在于，该模型求出的线路故障率与当时的气象条件相关，随气象指标的变化而变化。

输电线路的结冰速度［7］可表示为

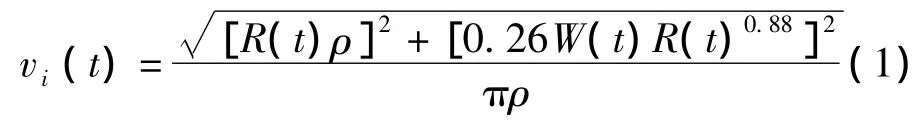
式中:W(t)为输电线路所在地的实时风速;R(t)为输电线路所在地的实时降雨速率;ρ为冰的密度。

输电线路的载冰量表达式为结冰速度vi(t)从0到t上的积分［8］，从而T时刻其表达式为

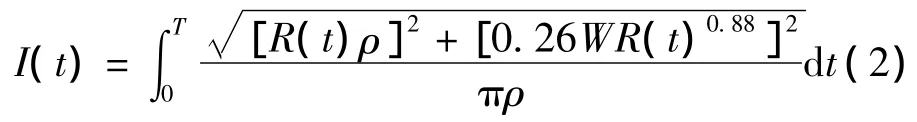
指数函数能够很好地拟合载冰量和线路故障率的关系［8］，因此本文采用指数函数对载冰量I(t)和故障率PFOR的数学关系进行拟合，其表达式［9］为

式中:k为衰减系数;ξ为阻尼系数。拟合函数式能反应在大规模冰灾时，载冰量越大元件越容易故障的特点。线路载冰量与故障率的关系如图2所示，图中dload为设计载冰量［9］。

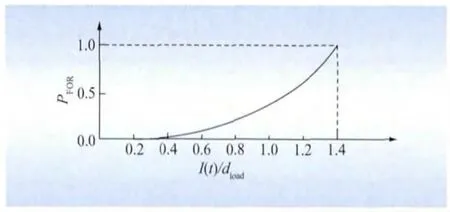
图2 载冰量与线路故障率的数学关系Fig.2 Relationship between ice load and outage rate

将式(2)代入式(3)，则能求得线路故障率PFOR与气象条件、冰灾持续时间的关系为

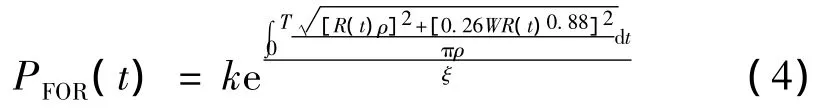
2.2 蒙特卡洛风险评估法(MC法)

冰灾的特点是发生概率小，但是一旦发生则可能引起多条线路同时断线，对电力系统造成极大影响。因此MC法具有研究冰灾下电网风险的优势，它的依据是:(1)每个元件的状态能通过概率采样确定;(2)系统状态是所有元件状态的组合。系统中的每一个元件拥有2种状态的马尔可夫模型，如式(5)所示，每个元件正常运行或者故障［10］

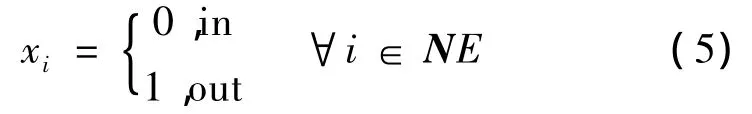
式中NE为元件的总数，各元件的状态取决于它的故障率，元件的状态组合决定了整个系统的状态。

假设Q(s)是待求的风险指标的估计值，则Q(s)的精确度由方差系数SC(s)表示，SC(s)的定义如式(6)所示。当风险指标估计值Q(s)有一个置信区间时，如式(6)所示，就可以作为蒙特卡洛迭代的停止条件。

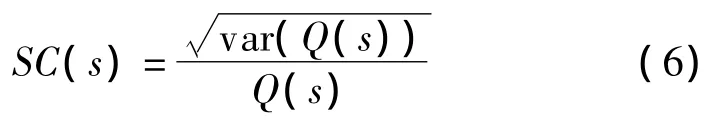
2.3 最优潮流模型

(1)定义以失负荷价值最小的目标函数为

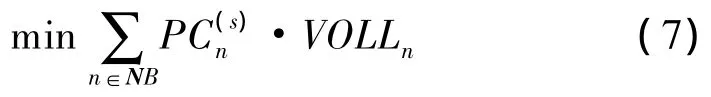
式中:PCn为n节点的失负荷量;VOLLn为n节点单位负荷量的价值［11］;n是节点标号;NB为节点数;s为第s次抽样。

(2)有功功率平衡约束式为

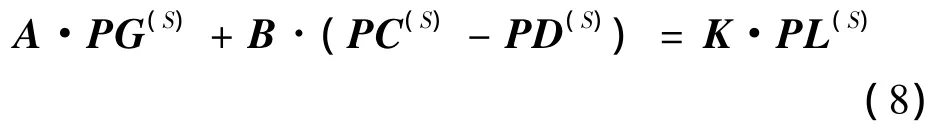
式中:A为发电机节点的关联矩阵;B为负荷关联矩阵;K为节点－支路关联矩阵;PG是发电功率向量;PD为负荷功率向量;PC为失负荷量向量;PL为线路潮流向量。

(3)支路潮流等式约束式为

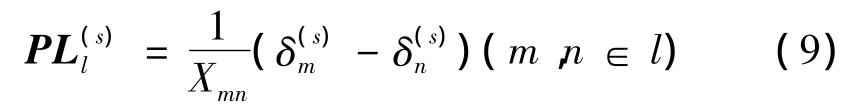
式中:PL是线路潮流向量;Xmn是m和n节点间的电抗;δ是节点电压相位角;l是线路标号。

(4)发电机组出力约束式为

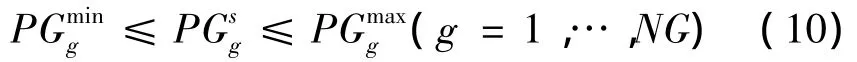
式中:g是发电机组标号;NG是发电机数;PGg是g的发电功率;、是发电功率界限。

(5)节点失负荷约束式为

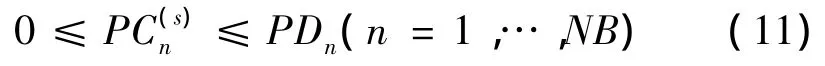
式中:n是节点标号;NB是节点数;PCn表示n节点的失负荷量;PDn为n节点负荷功率。

(6)支路潮流不等式约束式为

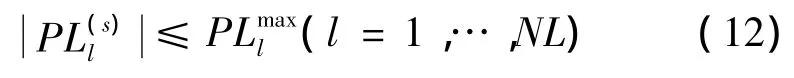
式中:l是线路标号，NL是线路数，PLl表示l的线路潮流为线路潮流界限。

2.4 冰灾风险指标的建立

每一次蒙特卡洛抽样后，得到特定的系统事故状态，能计算出相应的失负荷量。每一种事故下的失负荷价值可以考虑为事故带来的后果，如果乘以该种事故发生的概率，则可以得到该事故的风险。

因此定义电网的冰灾风险指标如下

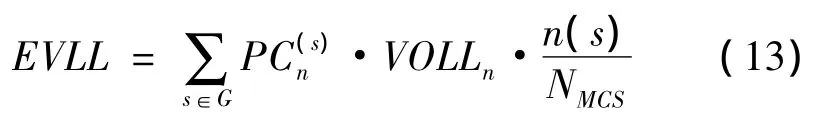
式中:EVLL的物理意义为冰灾下系统“失负荷价值期望”，即失负荷价值与概率的乘积为第s次抽样状态下的失负荷量;VOLLn为单位负荷量的价值;n(s)为状态s的发生次数;NMCS为抽样总次数;s为第s次抽样状态;G为系统状态的集合。

因此，通过对天气指标的采集，可以实时计算风险指标，从而电网工作人员能更准确地掌握电网面临的风险，尽可能减小冰灾对电网的伤害。

3 评估拓扑特性的理论原理和相关指标

研究拓扑特性对电网冰灾风险的影响，主要从以下2种拓扑特性分析:网状系数，圈长分布。网状系数反映了冗余路径的数量，圈长分布反映了冗余路径的长度。

平面上，与真实网络大小相同且最大不重叠边的数量相同的合成网络被称为极大平面图，被用于拓扑指标的归一化［12］。网络冗余度表示通过多种路径将电力传输到相同目的地的能力，它对电网的对灾害的耐受力有重要的影响。冗余路径的数量由网状系数M 表示，表达式如下［12］

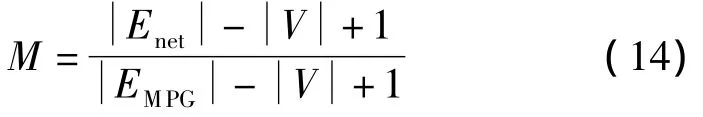
式中:|V|是电网中节点的数目;|Enet|是该网络中边的数量;|EMPG|是极大平面图中边的数量。网状系数越大表明网络的圈数越多。

圈的长度也影响电网对灾害引起的故障的反应［12-13］，因为路径越短，就越能限制电流在受损害的电网中的传播。利用式(15)求得含有3～5个节点的圈所占的比例(经过极大平面图归一化后)。求邻接矩阵A的k次幂，然后求所得矩阵的主对角线元素的总和，即能求得长度为k的圈在网络中所占的比例如下(经极大平面图归一化后)

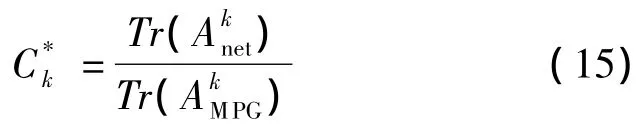
利用这些拓扑特征指标，能够估计系统受到冰灾后的风险。网状系数指标和圈长分布指标反映了潮流再次分布时，在特定的地理分布网络中，潮流可选择路径的数目和长度。由此推断，具有许多冗余路径，并且冗余路径长度较短(即网状系数大、圈长小)的系统正常运行的时间更长，可靠性更高，受到的风险更小。算例将验证以上推断。

冰灾下考虑多种拓扑特性的电网风险分析流程如图3所示。

4 算例分析

算例分为2部分:第1部分研究拓扑特性确定的电网风险评估，验证冰灾风险指标EVLL的有效性;第2部分对比具有不同拓扑特性电网的风险，验证网状系数M、圈长C对电网风险的影响。

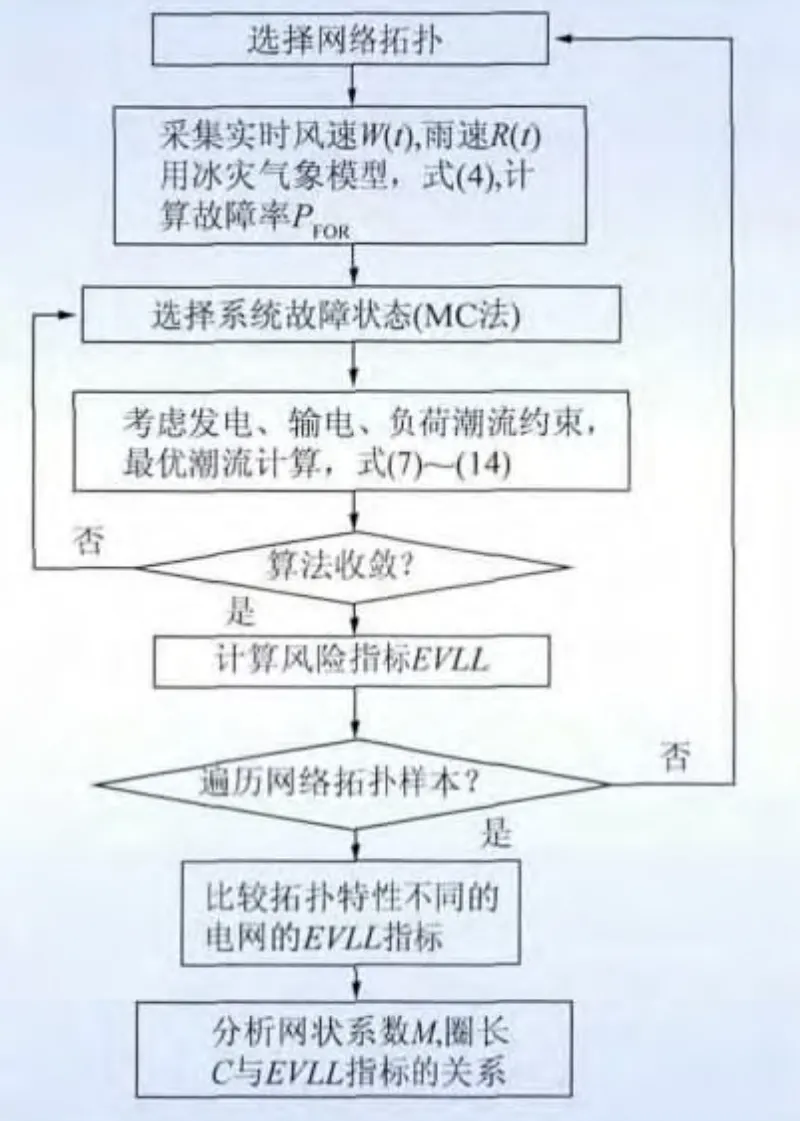
图3 冰灾下考虑多种拓扑特性的电网风险分析流程图Fig.3 Flow chart of power system risk analysis considering various topological characteristics under ice storm

算例采用IEEE30节点网络［14］，假设冰灾区域如图虚线框所示，线路 12—15、15—18、18—19、19—20、10—20、10—17、16—17、12—16 受到冰灾影响，如图4所示。

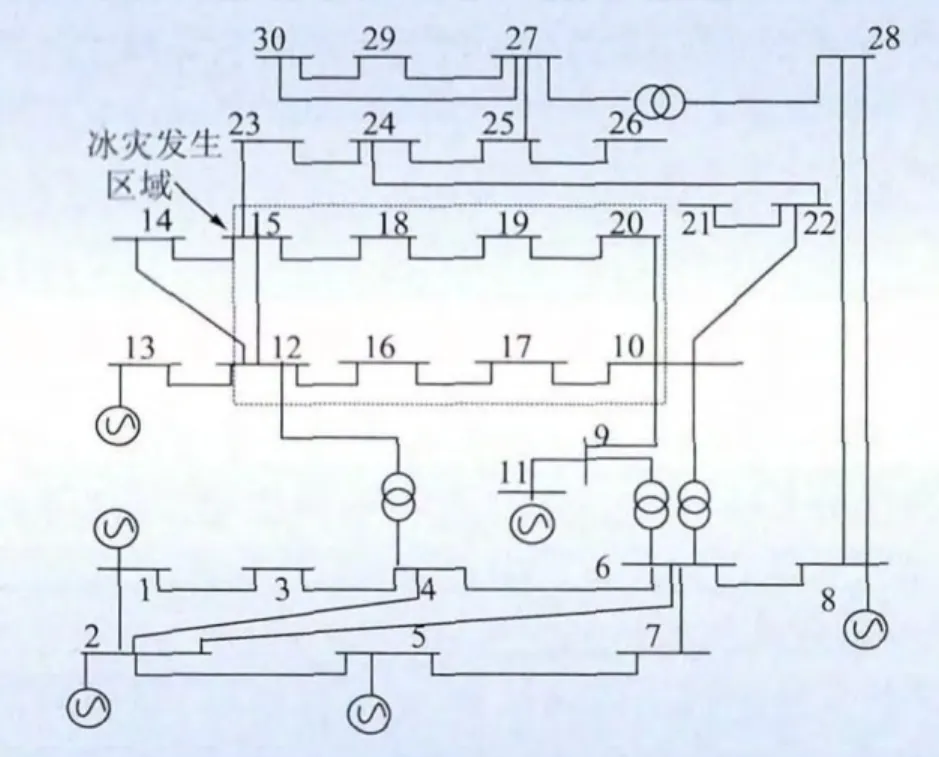
图4 IEEE30标准测试系统电气接线图Fig.4 Electric diagram of IEEE 30 standard test system

4.1 拓扑特性确定的电网风险评估

4.1.1 线路故障率计算

根据实际冰灾数据［15］，取4个冰灾下的气象场景，用式(1)求得结冰速度。表1为不同场景下，结冰速度与风速、雨速的关系。

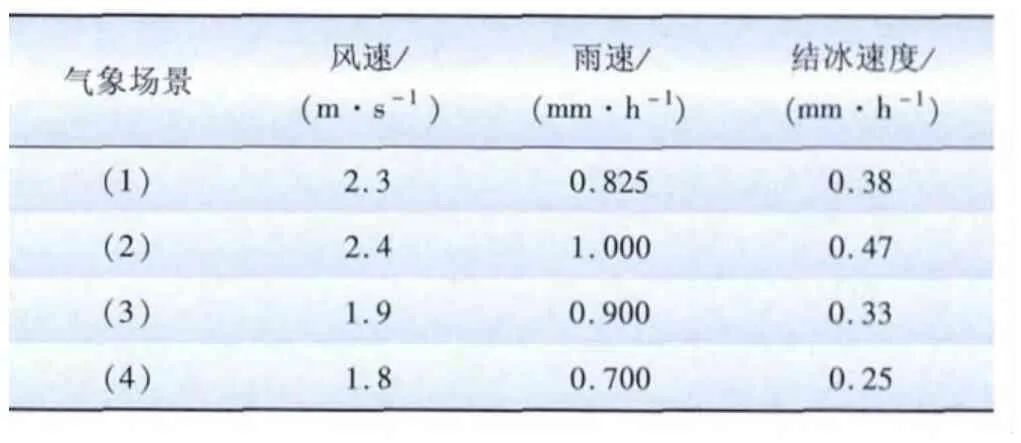
表1 不同冰灾气象场景下的结冰速度Tab.1 Icing speed under different ice storm weather scenarios

采用气象模型，即式(4)求取冰灾区线路故障率。图5为气象场景(1)下，线路故障率随冰灾持续时间的变化关系，由此可得任意时刻的线路故障率。

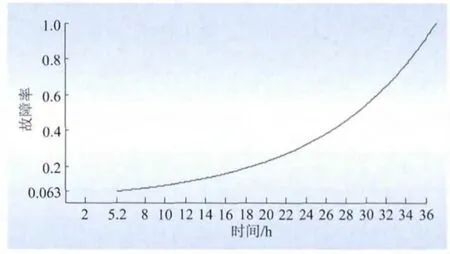
图5 气象场景(1)下线路故障率随时间变化的关系Fig.5 Relationship between line outage rate and time in ice storm scenario(1)

4.1.2 失负荷优化计算

表2列举了在气象场景(1)下系统可能发生的部分故障，以及对应的失负荷情况和价值。

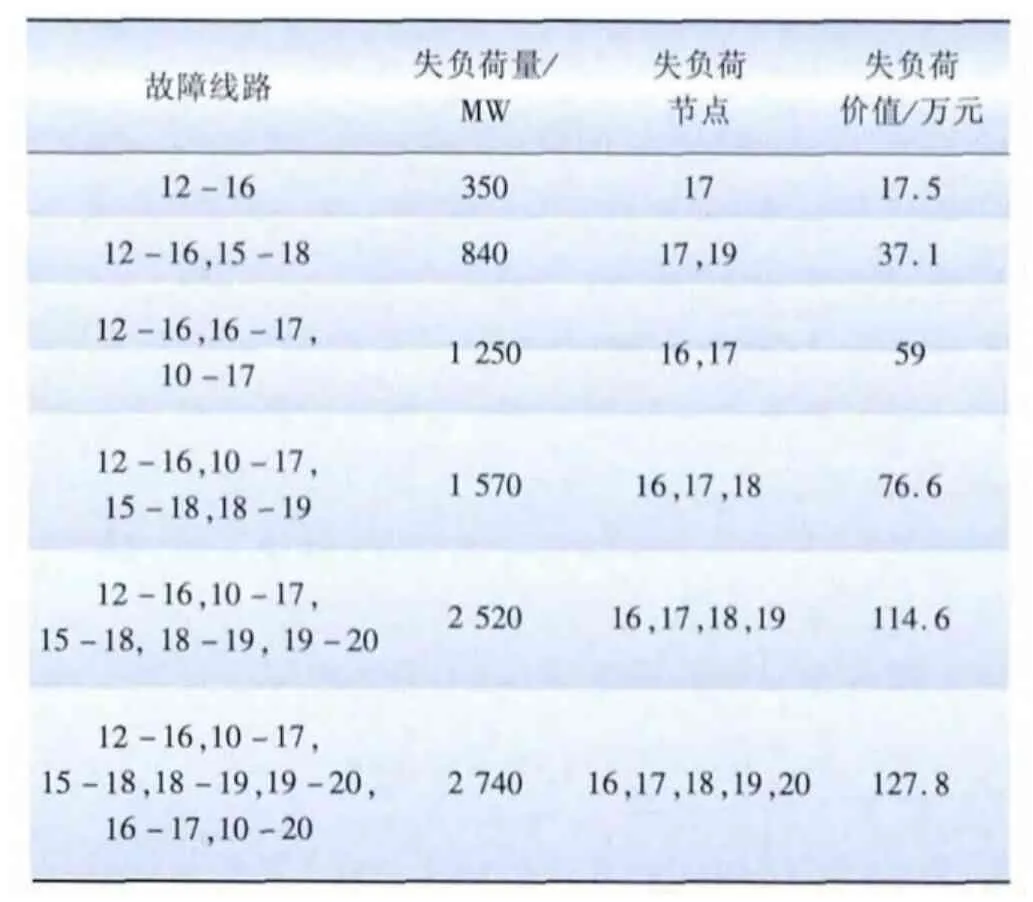
表2 冰灾下系统不同故障的失负荷情况Tab.2 Lost load of various failures under ice storm

4.1.3 风险指标EVLL计算

图6表示气象场景(1)和(2)下，风险指标“失负荷价值期望EVLL”随时间变化的趋势。

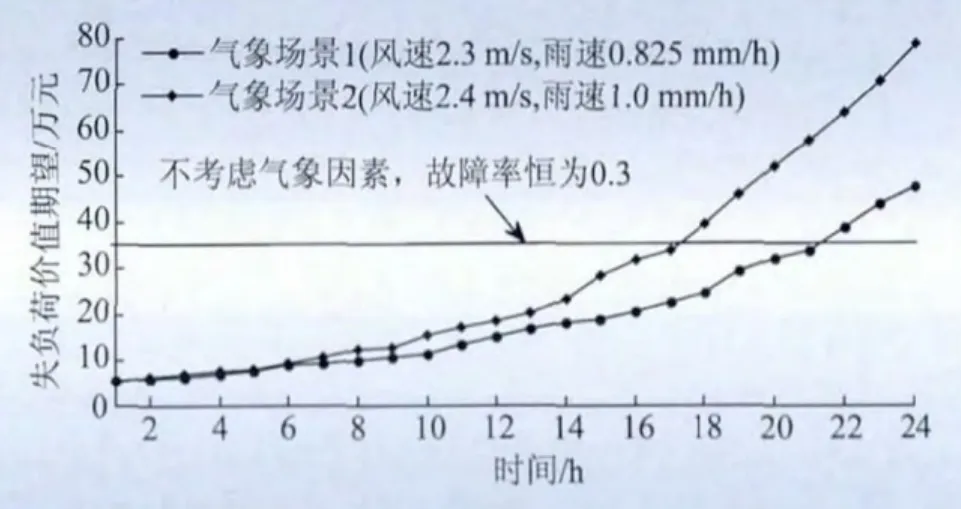
图6 不同气象场景下风险指标EVLL随时间变化的关系Fig.6 Relationship between risk index EVLL and time under different weather scenarios

图6表明在气象条件一定的情况下，风险指标EVLL与冰灾持续时间呈正相关。如图6所示，在5 h内，风险值增长率小;5 h后，风险值不断上升，且增长率增大。该结果符合客观实际:冰灾早期，线路故障率较小，系统发生多条线路同时断的概率较小;冰灾后期，线路故障率上升，系统受到的威胁愈加严重，其承受的风险也越来越大。

图6也表明，气象场景(2)比(1)风险指标EVLL更高，且增长率更高。该结果符合客观实际:由于气象场景(2)比气象场景(1)的风速、雨速更高，导致线路结冰速度更快，故障率更高，因此风险更高。

图6还显示，如果忽略气象条件、冰灾持续时间的影响，假设线路故障率恒定为较恶劣天气下的固定值0.3，则风险值也是固定值。电网工作者将不能准确地掌握当前电网所受的风险大小，并且在冰灾后期，将严重低估电网所受风险。

算例验证了冰灾风险指标EVLL能有效地反映气象条件和冰灾持续时间的影响，符合客观实际。

4.2 具有不同拓扑特性电网的风险分析

4.2.1 电网拓扑特性比较

为了研究拓扑特性对电网风险的影响，设置具有不同拓扑特性的结构，如图7所示。原结构记为结构1;结构2增加了线路13—14和线路9—17;结构3增加了线路16—19和线路9—12。这3种结构具有不同的网状系数M和圈长分布C。

根据式(14)和式(15)，计算3种结构的拓扑特性指标，即网状系数M、圈长为3到5的路径所占比例，如表3所示。

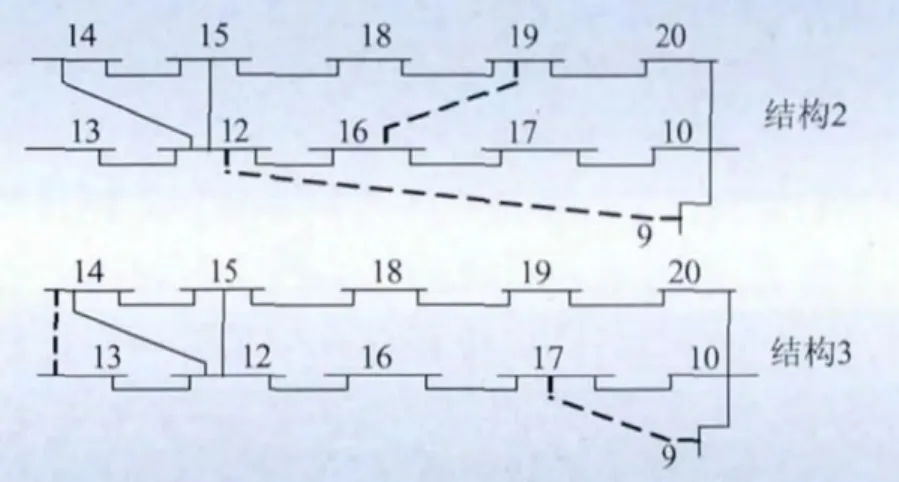
图7 冰灾区域2种拓扑特性不同的结构Fig.7 Two structures with different topological characteristics in ice storm damaged region

表3 3种不同结构的拓扑特性指标Tab.3 Topological characteristics indices with three structures

由表3可知，结构1的网状系数最小，圈长短(3到5)的路径所占比例最小;结构2与结构3的网状系数相同，但结构2中圈长短(3到5)的路径所占比例较小。由此说明，结构1的冗余路径数量最小，且具有最少量的短路径;结构2与结构3冗余路径数量相同，但结构3具有更多的短路径。因此结构3的冗余路径数量最多，并且具有最多的短路径。

4.2.2 不同拓扑电网的风险值EVLL比较

针对结构1～3进行冰灾下的风险评估，如图8所示，结构2的风险小于结构1(圈长分布近似相等)，说明网状系数M越大，电网风险越小;结构3的风险小于结构2，说明圈长短的路径比例越大，电网风险越小。

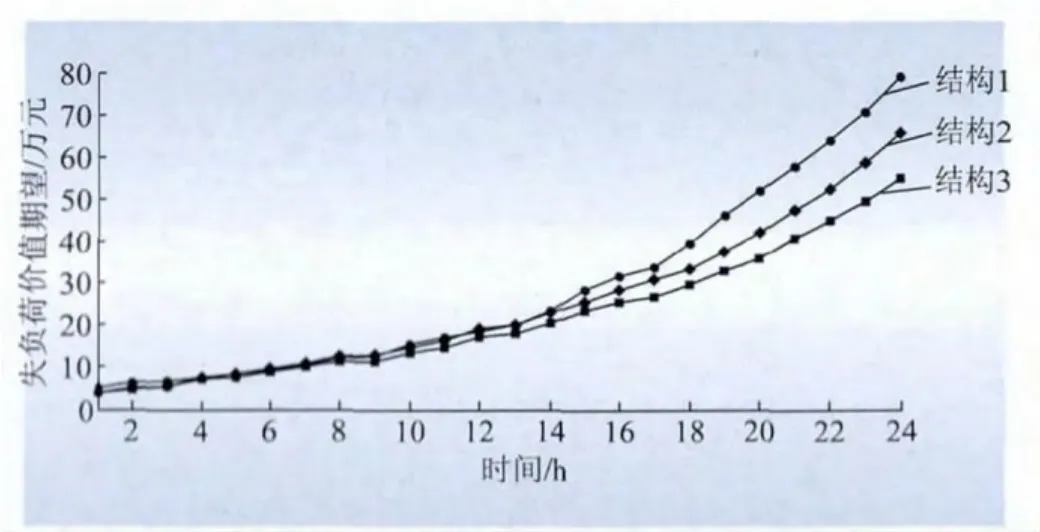
图8 不同拓扑的电网EVLL指标随时间变化的关系Fig.8 Relationship between risk index EVLL and time of power systems with different topologies

综上所述，网状系数M越大，圈长C短的路径比例越大，电网风险越小。因此，在规划电网拓扑时，应尽量采取网状系数M大，圈长C短的路径比例大的方案，从而使电网结构更坚强，更具有抵御极端灾害的能力。

5 结语

本文提出了一种冰灾下不同拓扑的电网风险分析方法，能够有效地反映拓扑特性对电网风险的影响，指导电网规划。由仿真计算结果可以得出以下结论:

(1)具有较大网状系数，较多短圈长路径的拓扑特性的电网，冰灾下电网风险较小。考虑具有较大网状系数，较多短圈长路径的拓扑结构，有助于进行抗灾能力强的电网规划。

(2)包含气象因子的风险指标能更客观反映冰灾对电网的影响。冰灾下线路故障率随时间增加呈指数上升，电网风险与气候恶劣程度、冰灾持续时间呈正相关关系。

［1］魏震波，刘俊勇，朱国俊，等.基于电网状态与结构的综合脆弱评估模型［J］.电力系统自动化，2009，33(8):11-14.

［2］恶劣气候电网如何应对［EB/OL］.［2013-07-29］.http://www.gkong.com/item/news/2009/09/40570.html.

［3］陈晓刚，孙可，曹一家.基于复杂网络理论的大电网结构脆弱性分析［J］.电工技术学报，2007，22(10):138-144.

［4］丁明，韩平平.基于小世界拓扑模型的大型电网脆弱性评估算法［J］.电力系统自动化，2006，30(8):7-10.

［5］孙强，张运洲，李隽，等.电网规划设计中的风险评估应用［J］.电力系统及其自动化学报，2009，21(6):18-21.

［6］王佳明，刘文颖，张建立.恶劣天气下的复杂电网连锁故障在线预警［J］.电网技术，2012，36(5):239-244.

［7］Jones K F.A simple model of freezing rain ice loads［J］.Atmospheric Research，1998，46(1 －2):87-97.

［8］Brostrom E.Ice storm modeling in transmission system reliability calculations［M］.Stockholm:KTH Press，2007:33-38.

［9］王建学，张耀，吴思，等.大规模冰灾对输电系统可靠性的影响分析［J］.中国电机工程学报，2011，31(28):49-56.

［10］李丽，牛奔.粒子群优化算法［M］.北京:科学出版社，2006.

［11］Farzad P，Babak M，Mona R.An Approach for Daily Assessment of Active Power Reserve Capacity and Spinning Reserve Allocation in a Power System［C］//IEEE International Conference on Power System Technology，2010.

［12］Cardillo A，Scellato S，Latora V，et al.Structural properties of planar graphs of urban street patterns［J］.Physical Review E，2006，73(6):1-7

［13］Alon N，Raphael Y，Uri Z.Finding and counting given length cycles［J］.Algorithmica 1997，17(3):209-223.

［14］University of Washington，Power System Test Cases Archive［EB/OL］.［2013-07-29］.http://www.ee.washington.edu/research/pstca/

［15］黄强，王家红，欧名勇.2005年湖南电网冰灾事故分析及其应对措施［J］.电网技术，2005，29(24):16-19.