斯特姆——刘维尔本征值问题的自然边界条件

杨志坚

(西南民族大学电气信息工程学院, 四川 成都 610041)

斯特姆
——刘维尔本征值问题的自然边界条件

杨志坚

(西南民族大学电气信息工程学院, 四川 成都 610041)

系统地讨论了斯特姆—刘维尔本征值问题中, 存在自然边界条件的几种情况: 1、在求解区间[a,b]上, 函数k(x)有一级零点, 则在该零点处一定存在自然边界条件; 2、在求解区间[a,b]上, 函数k(x)有二级零点, 仅当q-2≤0时, 在该零点处存在自然边界条件; 3、求解区间[a,b]上, 函数k(x)有高于二级零点, 且斯特姆——刘维尔方程在该零点处存在一个有界解, 在该零点处才存在自然边界条件.

斯特姆——刘维尔本方程; 本征值问题; 分离变量法; 自然边界条件.

在数学物理方法中常见的几种偏微分方程在坐标系下分离变量时, 就会出现含参量的二阶线性非齐次常微分方程.如勒让德方程, 贝塞尔方程等.这些常微分方程都可以用斯特姆——刘维尔方程(以下简称S—L方程), S—L方程可表述如下:

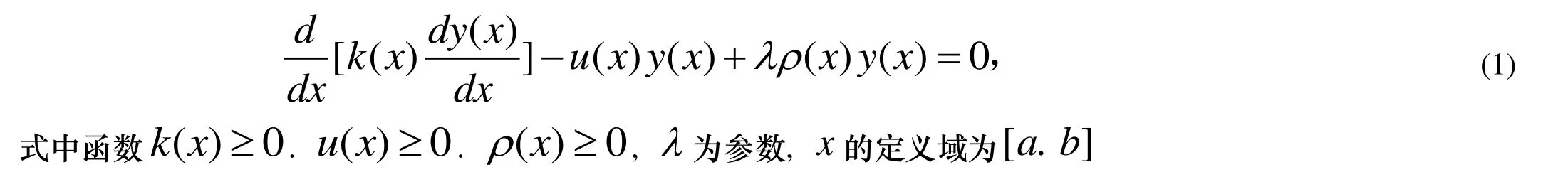
为了后面的讨论, 这里介绍一下二阶线性齐次常微分方程的标准形式

S—L方程附上边界条件即构成S—L本征值问题.在物理学中, 有一类边界条件是物理系统所处的具体物理环境的数学反映, 它需要人们具体规定, 这种边界条件称为人为边界条件, 简称边界条件.还有一类边界条件是物理系统本身的固有性质的数学反映, 它是客观存在的, 与物理环境无关, 称其为自然边界条件, 其数学表现为要求解函数单值, 有界等.

对自然边界条件的存在性问题, 大多数教材未系统叙述.这里分几种情况, 讨论如下:

定理1 函数k(x)有一级零点, 则一定存在自然边界条件.

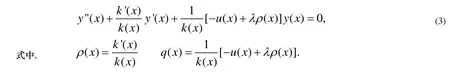
定理2： 函数k(x)有二级零点, 且q2≤0时存在自然边界条件.

证明: 为了求解指标方程, 先计算

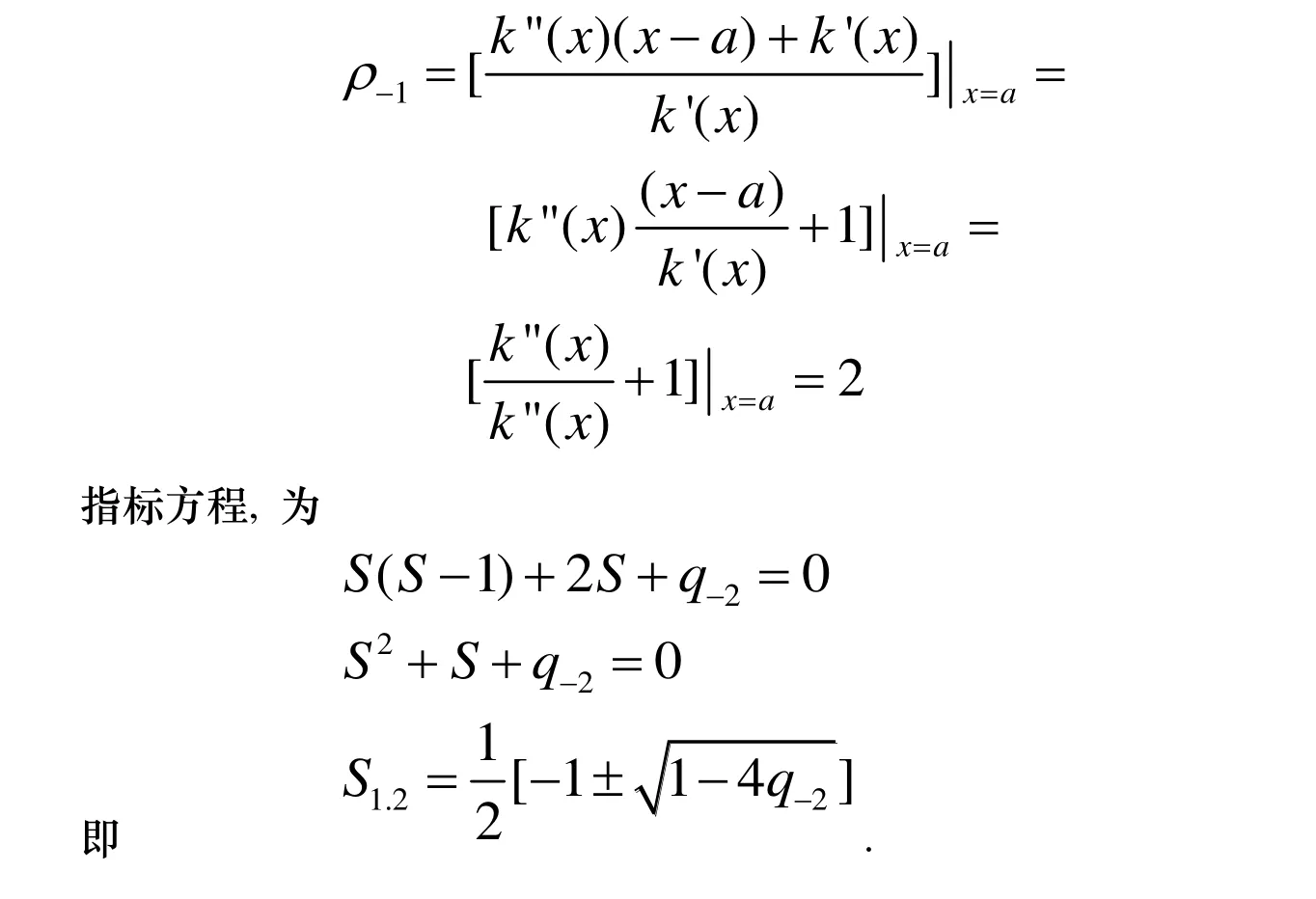
定理3 函数k(x)高于二级零点.且方程存在有界解时, 有自然边界条件.

关于上述定理及其证明方法, 需要说明一下: 1、该定理成立的条件有两个: 函数k(x)在求解区间上存在零点(不需要限制零点的级); S—L方程在该零点处存在一个有界解.后一个条件比较强.有时还是不必要的条件.如一级零点的情况; 而对二级零点, 只要成立就可以了.2、对于函数k(x)的高于二级零点的情况, 由于此时该零点总是S—L方程的非正则奇点.因此只能用二阶线性常微分方程的解理论来证明.

[1]王竹溪, 郭敦仁.特征函数概论[M].2版, 北京: 科学出版社,1979.

[2]R柯朗, D希尔伯特.数学物理方法[M].钱敏, 郭敦仁, 译.北京: 科学出版社, 1981.

[3]C A克罗斯顿, 数学物理方法导论[M].戴安英, 钱伯初, 译.北京: 科学出版社, 1982.

[4]梁思淼.数学物理方法[M].2版, 北京: 高等数学出版社, 1998.

[5]姚端正, 梁家宝.数学物理方法[M].北京: 高等数学出版社, 2010.

[6]胡嗣柱, 倪光炯.数学物理方法[M].北京: 科学出版社, 2002.

[7]郭敦仁.数学物理方法[M].北京: 人民教育出版社, 1978.

[8]F W 拜伦, R W富勒.物理学中的数学方法[M].熊家炯, 曹小平, 译.北京: 科学出版社, 1982.

[9]冯慈璋, 马西奎.工程电磁场导论[M].北京: 高等教育出版社, 2000.

[10]高建平, 张芝贤.电波传播[M].西安: 西北工业大学出版社, 2002.

[11]毛均杰, 刘荧.电磁场与微波工程基础[M].北京: 电子工业出版社, 2004.

[12]陆全康.数学物理方法[M].上海: 上海科学技术出版社, 1982.

[13]斯米尔诺夫.高等数学教程[M].聂灵沼, 译.北京: 人民教育出版社, 1979.

[14]南京工学院数学教研组.数学物理方程与特殊函数[M].北京: 人民教育出版社, 1979.

Nature boundary condition in Strum-Liouville problem

YANG Zhi-jian
(School of Electrical and Information Engineering, Southwest University for Nationalities, Chengdu 610041, P.R.C.)

This paper studies the several situations that have the nature boundary condition in the Strum-Liouville problem: (1) If there is a first-class zeros point in the function k(x) in x∈[a.b], then there is the nature boundary condition at the zerospoint in Strum-Liouville problem; (2) If there is a second_class zeros point in the function k(x) in x∈[a.b],and there is the condition i.e q-2＜0, then there is the nature boundary condition in Strum-Liouville problem; (3) If there are more second-class zeros point in the function k(x).in x∈[a.b], and there is a finite solution in Strum-Liouville problem, then there is the nature boundary condition at the zeros.

Strum-Liouville problem; eigenvalue problem; separating method; nature boundary condition

O175; O415

A

1003-4271(2014)06-0935-04

10.3969/j.issn.1003-4271.2014.06.23

2014-08-29

杨志坚(1958-), 男, 汉族, 四川人, 副教授.