观测量误差对新一代重力卫星任务的影响分析*

赵 倩 徐新禹 彭利峰

1)中国地震局地震预测研究所，北京 100036

2)武汉大学卫星导航定位技术研究中心，武汉 430079

3)武汉大学测绘学院，武汉430079

随着利用卫星跟踪卫星(SST)和卫星重力梯度(SGG)测量来确定地球重力场的技术日渐成熟［1－5］，卫星重力测量逐渐成为重力场研究的主要方法。［6－10］。重力测量卫星是一个复杂的观测系统，各类精密仪器不可避免地存在观测噪声和系统误差。研究各类测量误差量级对重力场反演精度的影响，是重力场解算的一个关键问题。尤其在新一代重力卫星任务中，使用激光测距系统能够将星间测距精度提高100 倍，而无拖曳控制系统则实时补偿卫星所受到的非保守力［11－12］，减少了加速度计这一参数的估计，因此定轨精度和星间测距精度对重力场反演的影响已经成为研究新一代重力卫星任务的重要问题。本文利用动力法分析卫星轨道和星间距离这两种观测量的误差量级和特性变化对最终重力场解算的影响。

1 仿真方法

采用动力法实现定轨及求解重力场位系数可表述为:利用卫星轨道的跟踪观测数据，估计轨道初值、卫星动力学的力模型参数和观测模型参数，在一定的最优化准则下使卫星轨道的跟踪观测值和估计值达到最佳拟合，即残差最小。动力法综合利用了卫星轨道运动的动力学约束和实际的跟踪观测信息，使用灵活，参数估计能力强［13－14］。

仿真过程包括两部分，同时仿真轨道数据和星间观测数据，并用它们进行重力场估计。第一部分使用一组真实模型进行仿真;第二部分则使用一组参考模型进行仿真。真实模型和参考模型之差表示目前模型的不确定度水平。

仿真实验中，GRACE 卫星高度350 km，轨道倾角89°，星间距离100 km［15］。仿真过程如下:首先利用真实模型生成一组轨道数据和卫卫跟踪数据SST，加入(各个量级)轨道数据和SST 跟踪数据的误差，将得到的数据作为真实观测量进行仿真实验;再使用参考模型同样生成一组轨道数据和卫卫跟踪数据作为参考观测量;从真实观测量中移去参考观测量，通过迭代得到卫星的初始状态向量、动力学力模型参数和观测模型中的其他待定参数;最后在重力场解算结果中加入参考模型值得到最终的解算结果，将其与仿真的真实模型作差，并转化为重力场的相关函数来表示目前误差条件下模型的精度，这里使用大地水准面表示模型的精度。

解算中同时考虑海潮、大气以及陆地水等时变信号的影响。由于本文研究的是观测量误差对重力场反演的影响，因此在轨道积分和重力场反演阶段均采用相同的时变信号模型，海潮模型为FES2004，大气模型为ECMWF，陆地水模型为GLDAS。表1给出仿真中静态重力场和各种时变信号模型。

表1 仿真实验中各种背景模型的选择Tab.1 Applied models for simulation

2 结果分析

2.1 轨道误差影响分析

低轨卫星的精密轨道确定是动力法高精度确定地球重力场的基础，重力卫星上装载有GPS 接收机来确保有连续的GPS 跟踪数据，用于精密轨道确定，同时也用于联系重力场估计和地球参考框架。每颗卫星装载激光反射器用于外部校准GPS 系统，地面激光测距联合GPS 数据进行精密定轨和重力场反演。目前重力卫星(如GRACE、GOCE 等)的定轨精度大多在2 ～3 cm，轨道精度对重力场的解算精度有较大影响。随着各种测量仪器和定轨方法的发展，卫星的轨道精度将会有数量级的提高，必须对重力场反演中由定轨精度造成的影响进行详细分析。当定轨精度为0.5、1、2、3、5 cm 时，仿真计算了不同轨道精度下重力场的解算精度，见图1。

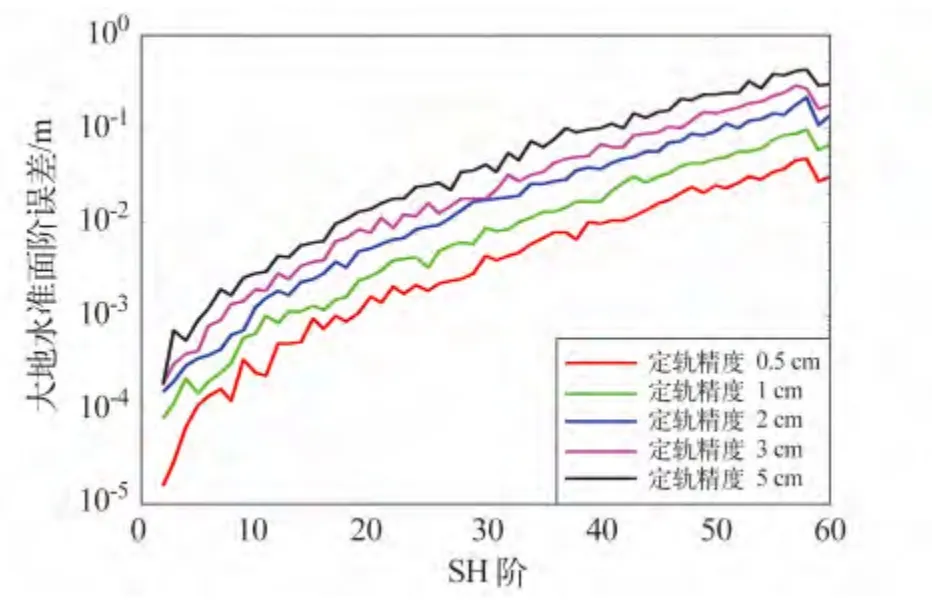
图1 仅有轨道数据、定轨精度不同时大地水准面阶误差变化Fig.1 The curve of geoid order error of different orbit determination precision for only using orbit data

由图1 可知，当仅采用轨道数据来反演重力场，即只利用高低跟踪GPS 测量值时，随着定轨精度的提高，重力场反演精度升高。轨道数据的精度对重力场低阶项较为敏感，对中高阶项则相对较差。显然，只利用高低跟踪数据来反演重力场不能达到更高的精度，但由于星间测距数据是表示两颗卫星之间的相对距离，能提供有限的关于卫星地心位置的绝对轨道信息，因此高低跟踪数据对于估计卫星轨道和重力场的长波信息至关重要。

2.2 星间测距误差分析

卫星轨道受地球系统的质量分布和迁移的整体影响，两颗GRACE 卫星的轨道所受摄动在不同地方会有差别，不同的摄动会反映在星间距离的变化上，而星间距离的变化被微波测距仪器以较高精度来记录。GRACE Follow-on 也同样会加载高精度的星间测距系统，测量的星间距离变化对重力场中高频信号更为敏感，可提高重力场反演的精度和分辨率。

在顾及非保守力误差影响下，利用星间距离变率作为观测值较星间距离有更大的优越性［16－17］。同时，在仿真过程中，重力场模型截断阶的选择对星间距离的影响也远比星间距离变率大，并且星间距离受重力场模型截断阶影响，不仅呈现周期性，而且有很明显的长期效应［14］。因此本文对星间测距误差的考虑主要是星间距离变率的误差。

目前GRACE 卫星上的星间距离变率测量精度约在10－6～10－7m/s，图2 为星间距离变率误差取为10－7m/s，定轨精度分别为0.5 cm、1 cm、2 cm、3 cm、5 cm 时，大地水准面的阶方差变化。当加入星间距离变率数据后，重力场反演精度较图1 有很大提高，反演精度仅在40 阶以下有所变化，40 ～60 阶时几乎一致，说明在中高阶系数中，定轨精度的差别几乎对这一频段没有影响，星间距离变率数据起主导作用。此外，本文还研究了重力场反演阶数不同时，星间测距精度变化对重力场解算结果的影响。图3 显示了定轨精度为1 cm，星间距离变率精度从10－5m/s 变化到10－9m/s 时，大地水准面阶误差的变化。实线为解算到90 阶的结果，点线为解算到60 阶的结果。可知，解算阶数高的重力场在高阶项的反演精度较差，并且解算精度越高，差别越明显。

为了更加深入分析这一现象，联合不同精度的星间距离变率数据和轨道数据解算重力场，如图4和图5。随着星间距离变率精度的提高，重力场反演精度不断提高。当星间距离变率精度较差时(10－6m/s)，随着定轨精度的提高，重力场反演精度在全阶次(60 阶)上都有提高;星间距离变率精度提高到10－7m/s 时，40 阶以上的重力场精度几乎不再变化;星间距离变率精度提高到10－8m/s 时，重力场精度只在10 阶以下的频段内有所区别;当星间距离变率精度提高到10－9m/s 时，重力场精度变化较大，尤其当定轨精度较差(5 cm)时，其重力场几乎在整个阶次上都明显比其他情况精度低。这说明，联合高低跟踪数据(轨道数据)和低低跟踪数据(星间距离变率数据)解算重力场，在定轨精度较高时，起主导作用的是低低跟踪数据，其精度越高，重力场反演精度也越高;但当定轨精度不太高(低于5 cm)，而星间距离变率精度提高到一定量级(低于10－9m/s)，定轨精度对重力场反演起到制约作用，在一定程度上阻碍了重力场，尤其是低阶重力场反演精度的提高。在当前星间测距精度的前提下，重力场反演对定轨精度要求不高，现有定轨精度(2 ～3 cm)完全能够保证高精度的重力场解算。但随着新一代激光测距技术的出现，其测距精度能提高1 000 倍，这时低轨卫星定轨的精度对于重力场反演会起到较为关键的作用。

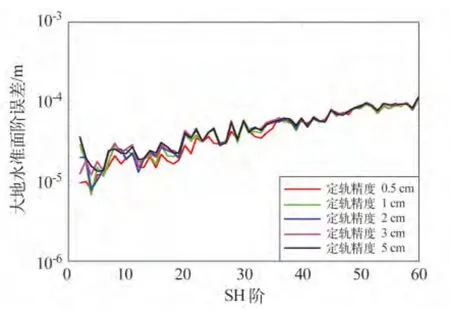
图2 星间距离变率为10 －7 m/s、定轨精度不同时解算的大地水准面阶误差方差变化Fig.2 The curve of variance of geoid order error with intersatellite range-rate of 10 －7 m/s and different orbit determination precision

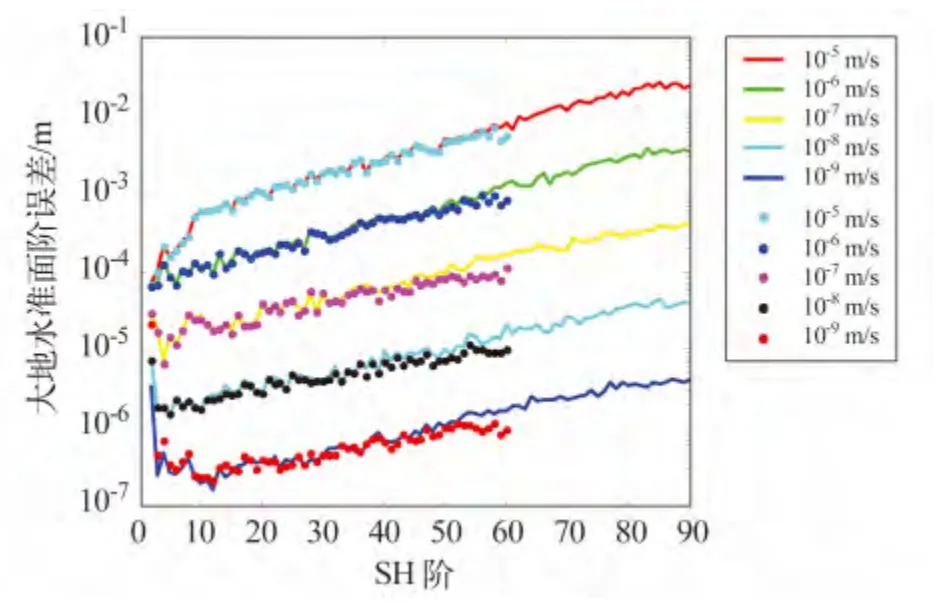
图3 轨道精度为1 cm、星间距离变率误差变化时解算的大地水准面阶误差变化Fig.3 The curve of geoid order error in 1 cm orbit determination error and different inter-satellite range-rate error

3 结 论

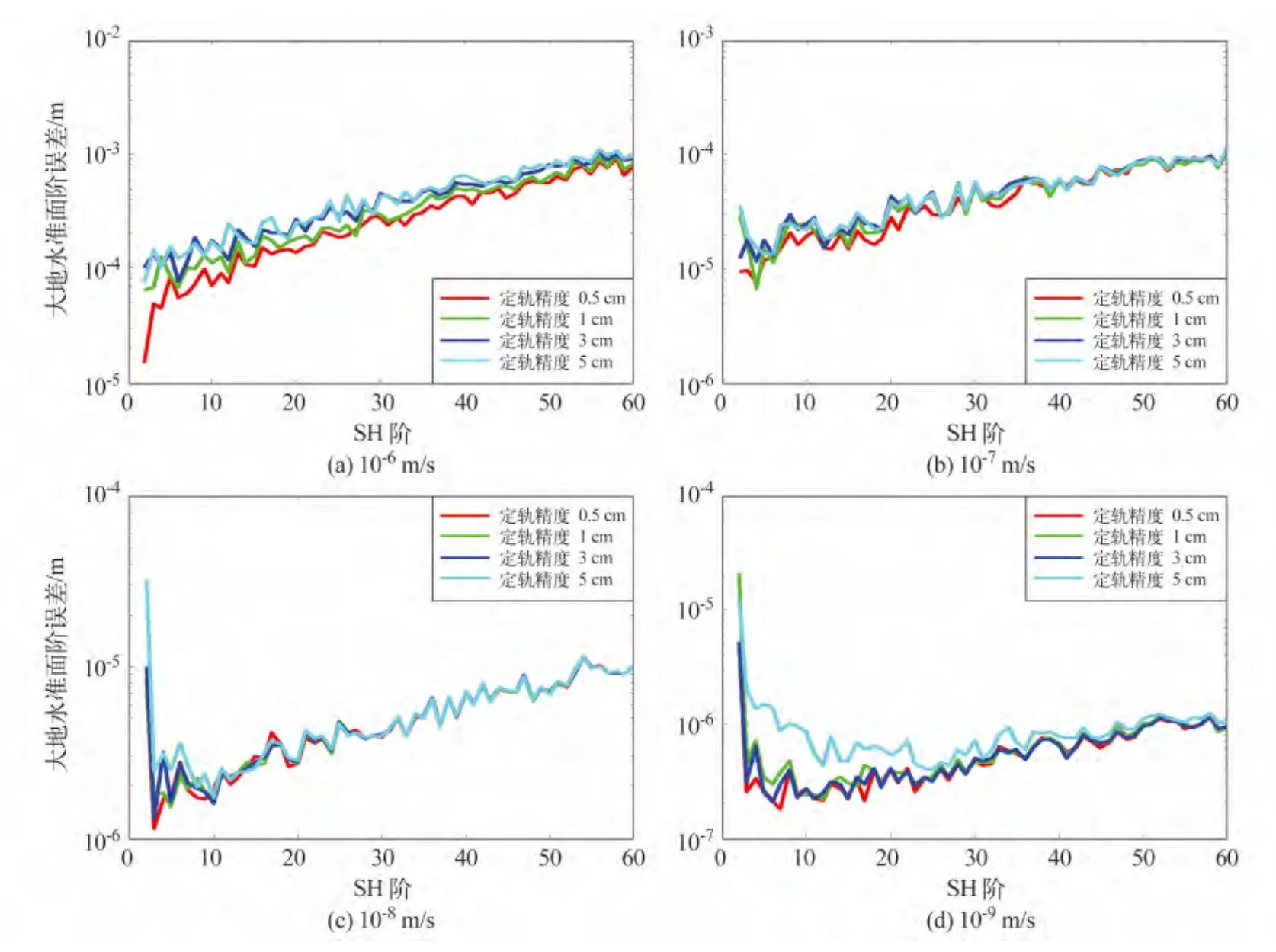
图4 各种轨道误差下解算的重力场模型与真实模型的大地水准面阶误差变化Fig.4 Comparison of geoid order error with real gravity field model to that with the determined model under different orbit determination errors

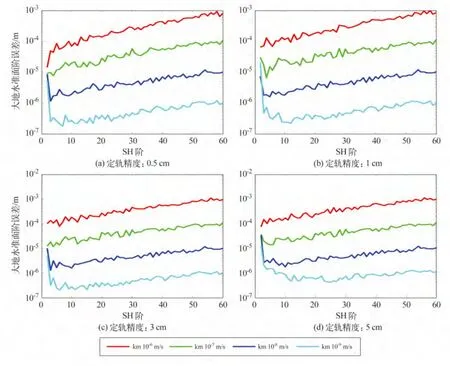
图5 各种星间测距精度下解算的重力场模型与真实模型的大地水准面阶误差变化Fig.5 Comparison of geoid order error with real gravity field model to that with determined model under different intersatellite ranging precision

轨道数据对重力场低阶项较为敏感，在当前定轨精度下，重力场解算中起主导作用的是低低跟踪数据，其精度越高，重力场反演精度也越高;但当星间距离变率精度提高到一定量级(如采用新的激光测距技术)，定轨精度对重力场反演尤其是低阶部分起到制约作用，在一定程度上阻碍了重力场反演精度的提高。在今后的新一代卫星重力任务中，若采用激光测距系统使得星间测距精度大幅度提升，如何同时提高定轨精度也是需要考虑的问题。

需要指出的是，各种误差的存在，如推进器系统对于卫星定轨和重力场反演会造成一定影响，在处理真实重力卫星数据时，必须要考虑它们的误差。在实际中重力场模型参数与各类误差参数之间的强相关性，在一定误差条件下，难以有效分离。因此本文的仿真结果只是在特定的情况下给出的，与实际情况不尽相同，但对于新一代重力卫星任务中各种误差系统对重力场的影响分析，具有极大的参考价值。

1 Gunter B C.Computational methods and processing strategies for estimating Earth’s gravity gield［D］.University of Texas at Austin，2004.

2 Tapley B D.GGM02 and improved Earth gravity field model from GRACE［J］.Journal of Geodesy，79:467－478.

3 徐新禹.利用参考重力场模型基于能量法确定GRACE加速度计校准参数的研究［J］.武汉大学学报:信息科学版，2008，33(1):72－75.(Xu Xinyu.Calibration of GRACE accelerometer using reference gravity field model based on energy balance approach［J］.Geomatics and Information Science of Wuhan University，2008，33(1):72－75)

4 郑伟.国际下一代卫星重力测量计划研究进展［J］.大地测量与地球动力学，2012(3):152－159.(Zheng Wei.Progress in international next-generation satellite gravity measurement missions［J］.Journal of Geodesy and Geodynamics，2012(3):152－159)

5 Ditmar P.Understanding data noise in gravity field recovery on the basis of inter-satellite ranging measurements acquired by the satellite gravimetry mission GRACE［J］.Journal of Geodesy，2012，86:441－465.

6 Chen J L.Seasonal global mean sea level change from altimeter，GRACE，and geophysical models［J］.Journal of Geodesy，2005，79(9):532－539.

7 胡小工.利用GRACE 空间重力测量监测长江流域水储量的季节性变化［J］.中国科学D 辑:地球科学，2006，36(3):225－232.(Hu Xiaogong.Seasonal variation of water distribution in Yangtze River basin from spatial gravity survey of GRACE［J］.Science in China Series D:Earth Sciences，2006，36(3):225－232)

8 周旭华.用GRACE 卫星跟踪数据反演地球重力场［J］.地球物理学报，2006，49(3):718－723.(Zhou Xuhua.Earth’s gravity field derived from GRACE satellite tracking data［J］.Chinese Journal of Geophys，2006，49(3):718－723)

9 汪汉胜.基于GRACE 时变重力场的三峡水库补给水系水储量变化［J］.地球物理学报，2007，50(3):730－736.(Wang Hansheng.Water storage change in Three Gorges water systems area inferred from GRACE time-variable gravity data［J］.Chinese Journal of Geophys，2007，50(3):730－736)

10 许厚泽.卫星重力测量及其在地球物理环境变化监测中的应用［J］.中国科学D 辑:地球科学，2012，42(6):843－853.(Hsu Houze.Satellite gravity and its application to monitoring geophysical environmental change［J］.Sci Sin Terrae，2012，42(6):843－853)

11 Loomis B.Simulations study of a follow-on gravity mission to GRACE［J］.Journal of Geodesy，2012，86:319－335.

12 Pierce R.Intersatellite range monitoring using optical interferometry［J］.Appl Optics，2008，47:5 007－5 018.

13 邹贤才.卫星重力资料分析的同解法研究及其仿真［J］.测绘学报，2010，39(4):344－348.(Zou Xiancai.Research on the simultaneous solution method for satellite gravity data analysis and its simulation［J］.Acta Geodaetica et Cartographica Sinica，2010，39(4):344－348)

14 邹贤才.卫星轨道理论与地球重力场模型的确定［D］.武汉:武汉大学，2007.(Zou Xiancai.Theory of satellite orbit and earth gravity field determination［D］.Wuhan:Wuhan University，2007)

15 赵倩.低轨道卫星重复周期的设计方法及其对重力场反演的影响［J］.测绘学报，2013，42(2):191－195.(Zhao Qian.Research on the design of LEO repetition period and itsinfluence on gravity field recovery［J］.Acta Geodaetica et Cartographica Sinica，2013，42(2):191－195，202)

16 沈云中，许厚泽.卫-卫跟踪重力卫星测量模式的模拟与精度分析［A］//大地测量与地球动力学进展［M］.武汉:湖北科学技术出版社，2004.(Shen Yunzhong，Hsu Houze.Simulation of recovering the geopotential model based on the satellite to satellite tracking gravity mission［A］//Progress in geodesy and geodynamics［M］.Wuhan:Hubei Science and Technology Press，2004)

17 周旭华.数值模拟估算低低卫-卫跟踪观测技术反演地球重力场的空间分辨率［J］.地球物理学报，2005，48(2):282－287.(Zhou Xuhua.Resolution estimation of earth gravity field recovery through the low-low satellite technology by numerical simulation［J］.Chinese Journal of Geophys，2005，48(2):282－287)