抗差Helmert方差分量估计在GPS/BDS组合定位中的应用*

高 晓 戴吾蛟

1)中南大学地球科学与信息物理学院，长沙 410083

2)湖南省精密工程测量与形变灾害监测重点实验室，长沙410083

1 引言

由于BDS 与GPS 均采用码分多址通信模式，GPS/BDS 组合定位优势更为明显。GPS 与BDS是两个独立的卫星系统，组合定位时须合理确定两类观测值权比，即确定观测值的方差-协方差阵，其数值取决于观测值随机噪声水平［1］。随着卫星不断运动，随机噪声发生改变，采用事先给定的固定权比进行组合定位显然是不合理的。Helmert 方差分量估计是一种通过迭代计算自适应确定不同类观测值权比的验后方差分量估计方法［2］，在数据处理领域得到了广泛的应用，并取得了良好的效果［3－5］。基于最小二乘原理的验后方差分量估计模型对粗差观测值很敏感，当观测值包含粗差时，粗差会“污染”随机模型，导致迭代收敛失真［6］，定位结果出现较大偏差。抗差Helmert 方差分量估计基于相关等价权原理确定自适应降权因子，通过降低粗差观测值的权重削弱其对定位结果的影响，提高定位精度。本文拟将该方法应用于GPS/BDS 组合伪距定位以及载波相位相对定位中以检验该方法的有效性与可行性。

2 抗差Helmert 方差分量估计模型

2.1 Helmert 方差分量估计模型

严密的Helmert 方差分量估计公式为［3］:

其中，n1、n2分别为两类观测值个数，N 为观测值设计矩阵，V 为观测值残差矩阵。解得与之后，重新调整两类观测值的权:

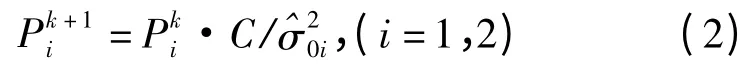
式中，C 为常数。

2.2 基于IGGIII 模型的抗差Helmert 方差分量估计模型

杨元喜［7］根据稳健估计思想构建观测向量抗差等价权，其中IGGⅢ模型为:

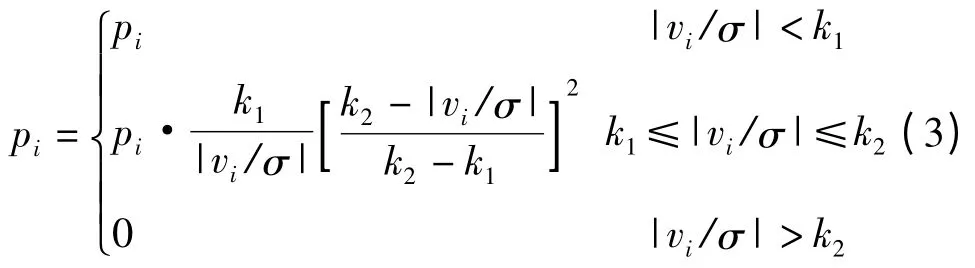
式中，k1、k2为常数，参照文献［8］，k1=1.5 ～2.0，k2=3.0 ～8.5。δ 为方差因子，其取值为:

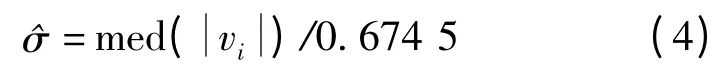
由于标准化残差向量v 可以较好地反映观测向量中的异常信息，当观测值带有粗差时，该异常信息将及时反映到残差向量中，利用该模型可以降低粗差观测值的影响，避免粗差污染定位结果，保证定位的可靠性。由于观测值精度不同导致不同类观测值组成的残差向量也存在系统性差异，采用自适应因子降权处理时无法准确分辨粗差与不同类观测值正确残差信息。因此，应先根据方差分量估计思想统一不同类观测值的中误差，确定不同类观测值合理权比，再利用上述模型抵抗粗差影响，从而提高定位精度与可靠性。

2.3 抗差Helmert 方差分量估计算法流程

1)根据高度角模型进行初始定权［9］，即

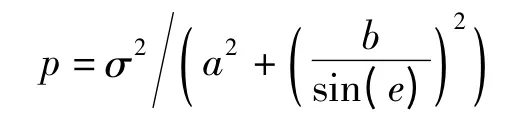
其中，e 为观测卫星高度角，a、b、σ 根据经验设定;

2)利用初始权阵进行首次平差计算，获取观测值残差信息;

3)按照式(1)计算GPS 与BDS 两类观测值方差估值)，重新定权;

4)按照式(3)计算自适应抗差因子，再次定权，式(3)中方差因子σ 可以按照式(4)确定;

5)基于抗差Helmert 方差分量估计模型重新进行平差计算，获取新的观测值残差信息;

3 算例分析

3.1 实验数据

采用GPS/BDS 双系统接收机于2012年11月28日在中南大学校本部采集4 小时数据，采样间隔设定为1 秒，共计14 400 个观测历元。统计测段内GPS 与BDS 观测卫星数如图1。可见，GPS 可视卫星数为6 ～10 颗。

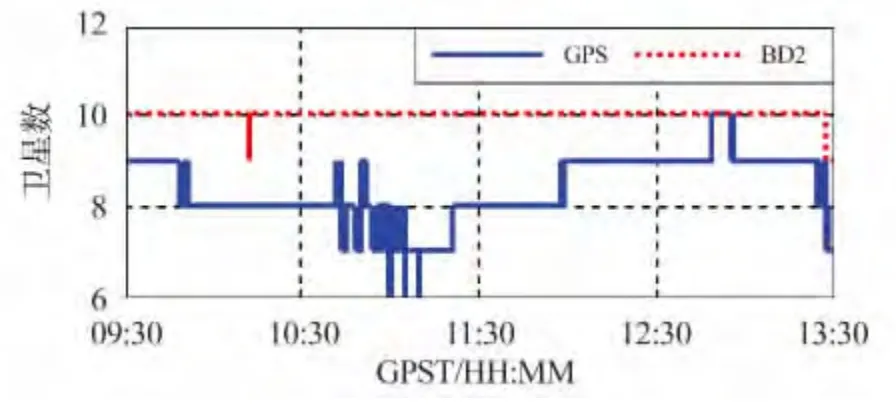
图1 GPS/BDS 观测卫星数Fig.1 Number of available satellites of GPS and BDS

图2 为测段内GPS/BDS 组合系统GDOP 值分时统计图。由图2 可知，当天组合系统卫星分布强度较高(GDOP 最小值为1.45，最大值为2.48，均值为1.82)，各历元GDOP 值均小于阈值(4.0)，测段内观测数据无异常。

3.2 解算结果分析

高度角模型与Helmert 方差分量估计模型不足之处在于无法抵御粗差影响。抗差Helmert 方差分量估计由于加入抗差模型能够较好地抵制粗差。为体现这一特点，随机选取C01 卫星8 个历元的C1码观测值，人为添加三倍中误差(30 m)的粗差，分别基于高度角模型、Helmert 方差分量估计模型以及抗差Helmert 方差分量估计模型进行组合伪距单点定位计算，结果如表1 与图3 所示。

从表1 和图3 可以看出，添加粗差的8 个历元基于不同模型定位结果差异显著。高度角模型无法抵御粗差的影响，定位结果出现明显偏差，水平方向与高程方向均呈现明显的“尖刺”状。当观测值包含粗差时，Helmert 方差分量模型明显收敛失真，特别是东西方向定位偏差更加明显。抗差Helmert 方差分量估计模型在三个方向均无明显震荡现象，真误差曲线较之其他模型更加平缓，可见抗差Helmert方差分量估计模型不仅可以合理确定GPS 与BDS组合伪距观测值权比，同时可以有效抵制粗差影响，提高定位精度与可靠性。

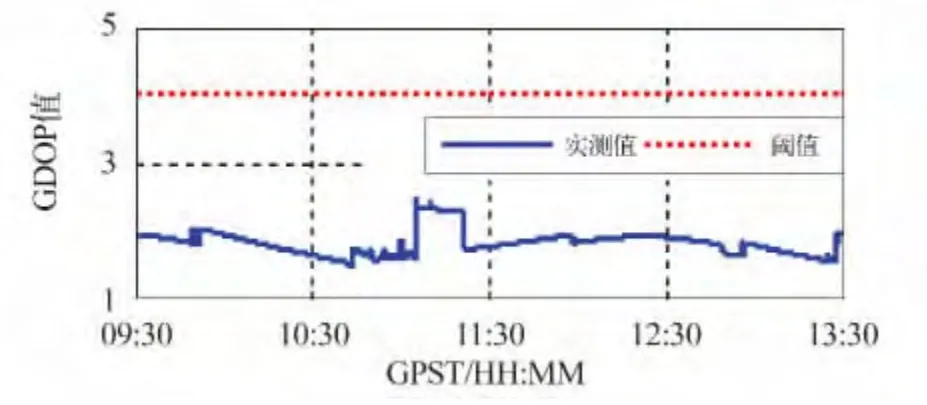
图2 GPS/BDS 卫星GDOP 值分时统计Fig.2 Statistics of time-share of GDOP for GPS and BDS

表1 不同定权方案伪距单点定位结果对比(单位:m)Tab.1 Comparison of results of pseudorange single point position with different stochastic models(unit:m)

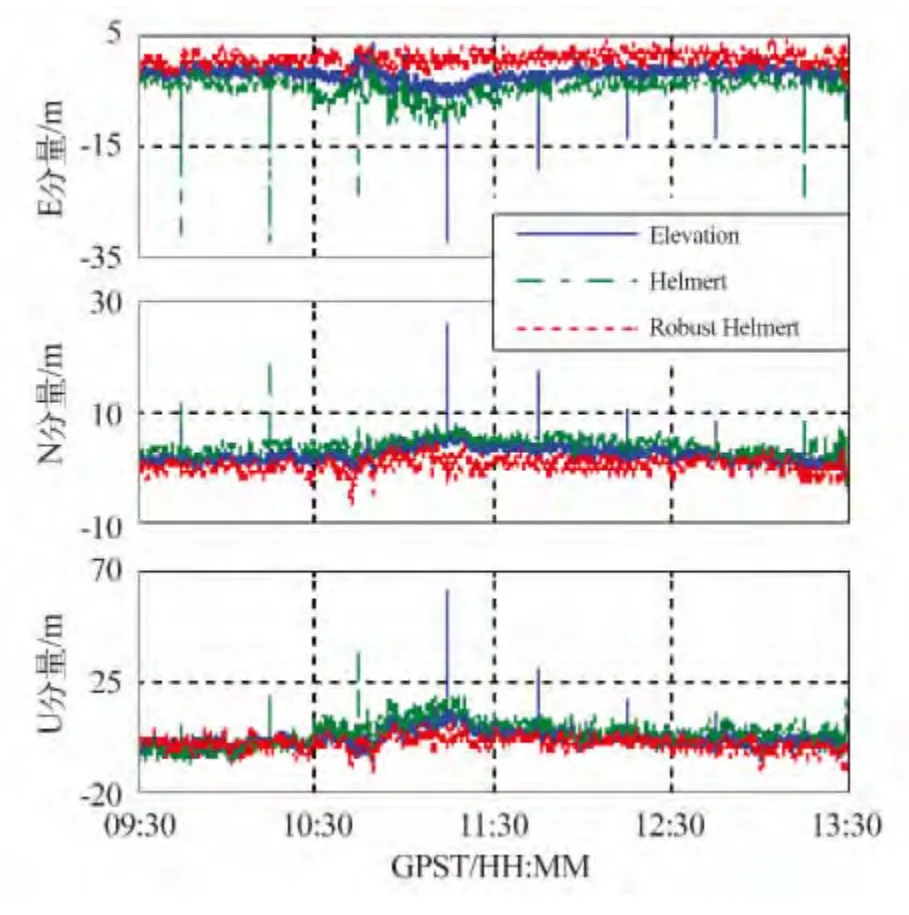
图3 不同定权方案组合伪距定位真误差序列Fig.3 Compareation of real errors for different models in combined GPS and BDS pseudorange position

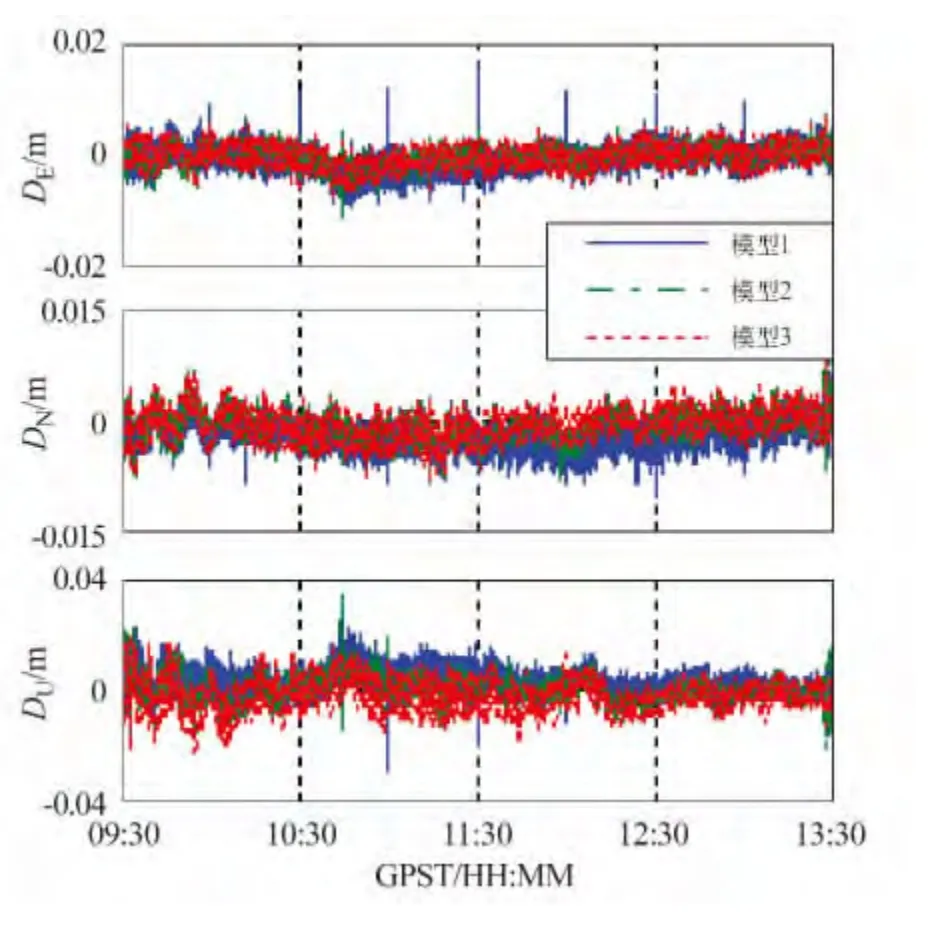
图4 不同定权方案组合相对定位真误差序列Fig.4 Compareation of real errors for different models in combined GPS and BDS pseudorange position

为检验抗差Helmert 方差分量估计模型对于载波相位观测值的有效性，随机选取C01 卫星7 个历元L1观测值，人为添加三倍中误差(0.6 周)的粗差，基于不同随机模型进行GPS/BDS 组合动态相对定位计算，结果如图4。同时，将添加粗差的7 个历元定位结果进行统计，结果如表2。

由图4 和表2 可以看出，高度角模型无法抵御粗差影响，7 个添加粗差的历元定位结果存在明显偏差，东西方向更加明显。Helmert 方差分量估计模型通过合理确定GPS 与BDS 两类观测值权比提高了定位精度，但是该模型存在收敛失真现象，特别是测段后期定位结果出现了明显的震荡现象，个别历元定位结果偏差甚至大于高度角模型，可见粗差已经“污染”随机模型导致收敛失真，降低了定位可靠性。抗差Helmert 方差估计模型较好地抑制粗差影响，7 个带有粗差观测值的历元定位结果与真值偏差较小，可见该模型有助于提高定位精度与可靠性。

4 结论

由于GPS 与BDS 存在系统性差异，且观测值随机噪声水平随卫星运动而发生改变，组合定位时依据固定权比进行定位是不合理的。Helmert 方差分量估计方法可以合理确定GPS 与BDS 两类观测值权比，提高定位精度。但当观测值存在粗差时，方差分量估计方法会出现收敛失真现象，导致定位结果偏差较大。基于IGGIII 模型的抗差Helmert 方差分量估计模型采用等价权的方法对粗差观测值进行降权处理，削弱甚至消除粗差观测值的影响，同时可以动态确定两类观测值权比，定位精度与可靠性均有提高。

1 何海波，杨元喜.GPS 观测量先验方差-协方差矩阵实时估计［J］.测绘学报，2001，30(1):42－47.(He Haibo and Yang Yuanxi.Real-time estimation of a prior variance-covariance for GPS observations［J］.Acta Geodaetica et Cartographica Sinica，2001，30(1):42－47)

2 高晓，戴吾蛟.基于方差分量估计确定GPS/BDS 组合定位先验权比［J］.大地测量与地球动力学，2013，(2):136－138.(Gao Xiao and Dai Wujiao.Determination of prior weight ratio in combination of GPS-BDS position based on variance component estimation，2013，(2):136－138)

3 段举举，沈云中.基于方差分量估计的GPS/GLONASS 组合点定位［J］，测绘通报，2011，(4):4－6.(Duan Juju and Shen Yunzhong.GPS/GLONASS combined position using variance component estimation［J］.Bulletin of Surveying and Mapping，2011，(4):4－6)

4 范百兴，李广云.Helmert 方差分量估计在跨河水准测量中的应用［J］.测绘学院学报，2004(3)，21(1):27－29.(Fan Baixing and Li Guanyun.Application of Helmert-WF variance component estimation to river-crossing leveling［J］.Journal of Institute of Surveying and Mapping，2004(3)，21(1):27－29)

5 高俊强，胡灿.Helmert 方差分量估计在隧道贯通中控制导线平差的研究［J］.中国矿业大学学报，2006(1)，35(1):125－129.(Gao Junqiang and Hu Can.Study on application of Helmert variance estimation to tunnel runthrough control traverse difference［J］.Journal of China University of Mining ＆ Technology，2006(1)，35(1):125－129)

6 刘长建，马高峰.Helmert 方差分量估计的粗差检验与抗差解［J］.测绘信息与工程，2002，27(6):5－7.(Liu Changjian and Mu Gaofeng.Blunder test and robust solution of variance component estimation for Helmert type［J］.Journal of Geomatics，2002，27(6):5－7)

7 Yang Y X.Robust estimation of geodetic datum transformation［J］.Journal of Geodesy，1999，73:345－349.

8 杨元喜，宋力杰，徐天河.大地测量相关观测抗差估计理论［J］.测绘学报，2002，31(2):95－99.(Yang Yuanxi，Song Lijie and Xu Tianhe.Robust parameter estimation for geodetic correlated observations［J］.Acta Geodaetica et Cartographica Sinica，2002，31(2):95－99)

9 戴吾蛟，丁晓利，朱建军.基于观测值质量指标的GPS 观测量随机模型分析［J］.武汉大学学报(信息科学版)，2008，33(7):718－722.(Dai Wujiao，Ding Xiaoli and Zhu Jianjun.Comparation of GPS stochastic models based on observation quality indices［J］.Geomatics and Information Science of Wuhan University，2008，33(7):718－722)