利用非差观测量确定导航卫星精密轨道与钟差的方法研究*
2014-02-13刘伟平郝金明于合理田英国
刘伟平 郝金明 于合理 田英国
(信息工程大学导航与空天目标工程学院,郑州 450001)
1 引言
导航卫星精密定轨和钟差确定的研究起步于20世纪70年代,并随着GPS 的建成运行,得到了持续的发展[1-3]。特别是90年代IGS 成立以来,轨道和钟差的确定精度不断取得突破,目前,IGS 最终轨道精度优于2.5 cm,最终钟差精度优于0.075 ns[4,5]。进入21世纪以来,我国按照“三步走”战略,开始建立具有自主知识产权的北斗卫星导航系统(BDS)。系统从2012年底起正式提供亚太区域服务,目前正朝着全球组网的方向发展[6]。为了促进北斗的建设和推广应用,相关单位正在积极筹建全球连续监测评估系统(iGMAS,international GNSS Monitoring and Assessment),精密轨道与钟差确定是其核心业务[7]。采用何种体制方法进行精密定轨和钟差估计,是值得研究的问题。
根据观测量组差方式不同,导航卫星精密定轨和钟差确定的方法可分为双差处理方法和非差处理方法。双差处理方法可消除或减弱大部分误差源的影响,并保持模糊度的整数特性,在一些大型GNSS数据处理软件(如Bernese、GAMIT 等)中得到了广泛应用[8,9],特别是在GPS 系统建设初期相关误差模型还不甚完善时,发挥了重要作用。近些年来,随着误差模型的不断精化以及观测数据质量的不断改善,非差处理方法也逐渐引起了研究人员的重视,相比双差处理,非差处理不损失观测信息,观测量间的独立性较好,可规避复杂的相关权问题,能够同时估计轨道和钟差,在算法实现上更加简单明了,近几年发展起来的软件系统(如EPOS、PANDA 等)大多采用了非差处理方法[10,11]。
为了进一步探讨非差数据处理技术在导航卫星精密定轨和钟差确定中的实际应用效果,为我国北斗卫星导航系统精密轨道与钟差确定的体制方法及软件系统研制提供参考,本文研究了利用非差观测量确定导航卫星精密轨道和钟差的方法,给出了数据处理的基本原理及具体实现策略,并结合GPS 实测数据,对其处理精度进行了初步分析。
2 方法原理及实现
由于初始模糊度与钟差参数不可分离,如果仅利用相位观测数据,只能估计钟差相对于参考历元的变化值,本文通过联合使用伪距和相位数据来解决这一问题,为进一步提高处理精度,还对伪距进行了相位平滑,并在处理中,对相位和伪距进行了消电离层组合,基本观测方程为:

式中,t表示观测历元,f1、f2表示双频观测量的两个频率,P1、P2表示伪距观测量,Φ1、Φ2表示相位观测量,ρ(t)表示星地几何距离,dts(t)、dtr(t)分别表示卫星钟差和接收机钟差,dρtrop(t)表示对流层延迟,N表示相位模糊度,λc表示消电离层组合相位观测量的波长,c表示光速,εP、εΦ表示其他未模型化的误差。
对式(1)、(2)进行线性化,有
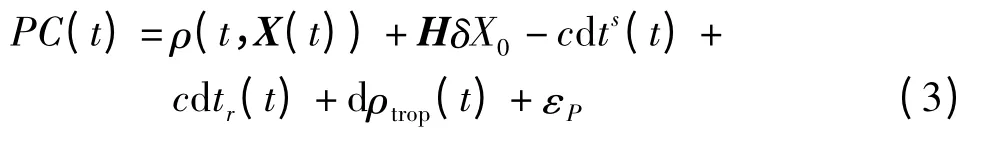

根据最小二乘批处理原理,利用线性化的观测方程即可进行轨道和钟差参数的估计。处理中,在整个时段上只估计一组轨道参数;钟差参数作为历元参数在每个观测历元都要进行估计;每4 小时估计一组对流层天顶湿分量。为了提高处理效率,首先对大量的钟差历元参数进行预消除,待完成轨道估计之后,再回代求解钟差参数。整个数据处理流程见图1。
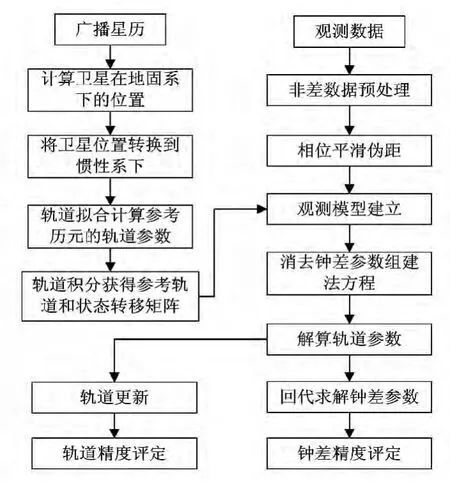
图1 数据处理流程图Fig.1 Flow chart of data processing
3 算例
为了验证该方法的实际处理效果,采用2010年5月12日全球均匀分布的34 个跟踪站一天的GPS观测数据进行实验,原始采样为30 s。测站分布见图2,具体的处理策略见表1。
解算的轨道与IGS 最终星历进行对比,以均方根误差(RMS,Root Mean Square)为标准考察定轨精度;解算的钟差与IGS 最终钟差进行对比,以确定钟差估计精度。为避免由于解算钟差与IGS 最终钟差的参考钟选取方法不同而引入系统差,使用文献[12]所提出的“二次差比对”方法来评定钟差精度,其方法为:首先选择同一个参考卫星,将解算钟差与IGS 最终钟差分别与各自的参考卫星钟差作差,消除基准钟不同对钟差结果的影响,而后再在各自消除基准钟影响的计算结果之间作差,所得的“二次差”能够较好地反应钟差参数的估计效果。此外,由于钟差系统差部分对精密定位的影响可以被模糊度参数吸收,因此考察钟差解算结果的波动情况更具实际意义。这里采用“二次差”的标准差(STD,Standard Deviation)作为考察钟差解算效果的标准。

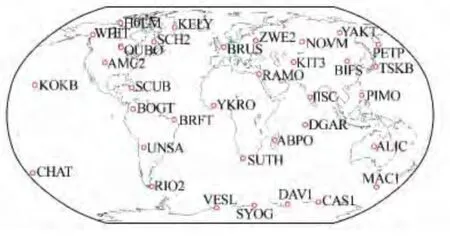
图2 测站分布图Fig.2 Distribution of Stations

表1 数据处理策略Tab.1 Strategy of data processing
式中,Δi表示第i 历元的误差;表示所有误差的均值;n表示历元总数。
图3 给出了各卫星R、T、N 方向的定轨均方根误差(RMS);图4 给出了G02 星R、T、N 方向的定轨误差变化情况,表2 对G02 星R、T、N 方向的定轨误差进行了统计,其他卫星的情况与G02 星类似,不再逐一给出。
由图3 可见,R 方向的定轨精度普遍高于T、N方向,这是由于GNSS 观测量对R 方向轨道运动更为敏感所致,经计算,所有卫星R、T、N 方向的平均RMS 为0.032 m、0.084 m、0.078 m。由图4 的结果可见,卫星定轨误差具有周期性,这一周期性与卫星运行周期是一致的,不同卫星的定轨精度存在一定差异,可能与各个卫星的观测数据质量有关;由表2对G02 星定轨结果的统计可见,G02 星轨道精度在厘米量级,定轨结果良好。
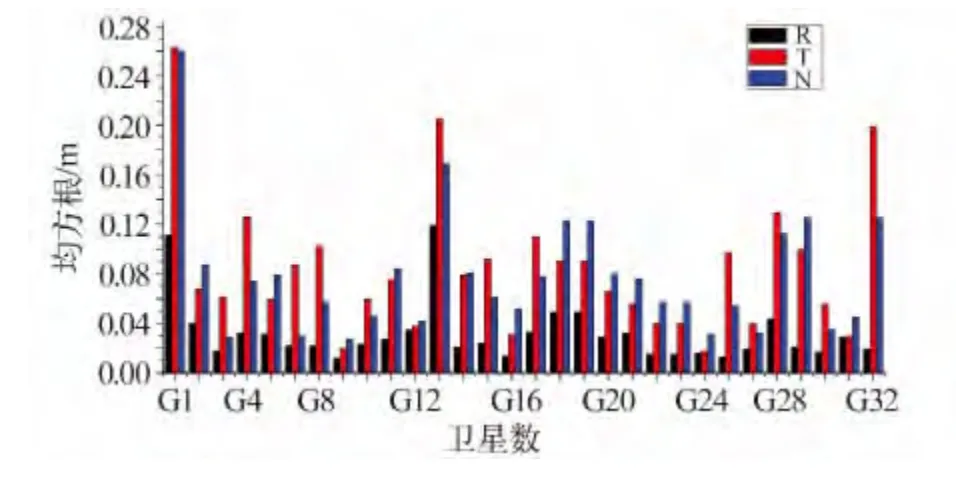
图3 精密定轨结果Fig.3 Results of precise orbit determination
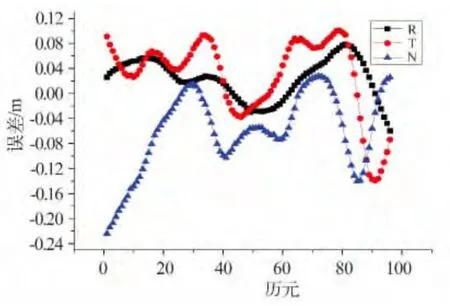
图4 G02 星定轨结果Fig.4 Results of orbit determination for G02
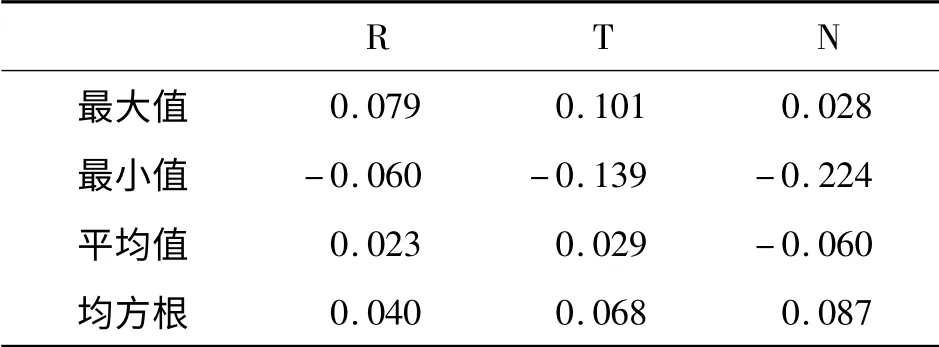
表2 G02 星定轨结果统计表(单位:m)Tab.2 Statistics of orbit determination for G02(unit:m)
选择G02星的星钟作为参考钟,图5给出了各卫星钟差“二次差”的标准差(STD)。由图5 可见,各卫星钟差确定结果精度比较均匀,所有卫星钟差“二次差”的平均STD 为0.18 ns。
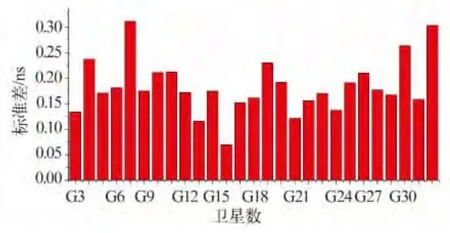
图5 钟差确定结果Fig.5 Results of clock offset determination
4 结论
利用全球均匀分布的30 余个测站一天的观测数据,通过非差数据处理,定轨精度R、T、N 方向分别达到0.032 m、0.084 m、0.078 m,钟差确定精度达到0.18 ns。需要说明的是,本文结果与IGS 最终精密产品的精度还有一定差距,主要原因是本文使用的测站数量较少且定轨弧段较短,后续仍需进一步研究增加测站数目及多天轨道合成的相关处理方法。
致谢感谢全球连续监测评估系统( iGMAS)信息工程大学分析中心对本文工作的帮助和支持!
1 Yunck T P,Wu S C and Wu J T.Strategies for sub-decimeter satellite tracking with GPS[A].Proceedings of IEEE position,location and navigation symposium 1986[C].Nevada:1986.
2 Beutler G,et al.Extended orbit modeling techniques at the CODE processing center of the international GPS service for geodynamic(IGS):theory and initial results[J].Manuscripta Geodaetica,1994,(19):367-386.
3 葛茂荣.GPS 卫星精密定轨理论及软件研究[D].武汉测绘科技大学,1995.(Ge Maorong.Study on theory and software of precise orbit determination for GPS satellite[D].Wuhan Technical University of Surveying and Mapping,1995)
4 IGS.International GNSS Service[ED/OL].http://igscb.jpl.nasa.gov.Date accessed:20/10/2011.
5 Jone M,Neilan R E and Rizos C.The International GNSS service in a changing landscape of global navigation satellite system[J].Journal of Geodesy,2009,83:191-198.
6 杨元喜.北斗卫星导航系统的进展、贡献与挑战[J].测绘学报,2010,39(1):1-6.(Yang Yuanxi.Progress,contribution and chanllenges of Compass/Beidou satellite navigation system[J].Acta Geodaetica et Cartographica Sinica,2010,39(1):1-6)
7 焦文海.iGMAS 体系架构及其进展[R].广州:2012.(Jiao Wenhai.Structure and current development of iGMAS[R].Guangzhou:2012)
8 Dach R,et al.Bernese GPS software version 5.0[M].Berne:University of Berne,2007.
9 Herring T A,King R W and McClusky S C.GAMIT reference manual[M].San Diego:MIT,2006.
10 Ge M,ChenJ and Gendt G.EPOS-RT:Software for realtime GNSS data processing[R].Vienna:EGU General Assembly,19th-24th Apr,2008.
11 李敏,赵齐乐,施闯.Panda 软件用户操作手册[M].武汉:武汉大学,2011.(Li Min,Zhao Qile and Shi Chuang.User manual of panda[M].Wuhan:Wuhan University,2011)
12 楼益栋.导航卫星实时精密轨道与钟差确定[D].武汉大学,2008.(Lou Yidong.Research on real-time precise GPS orbit and clock offset determination[D].Wuhan University,2008)
