GPS参考站观测与记录时间不一致问题的解决方法*
2014-02-13朱丽强
张 勇 朱丽强 王 建
1)苏州工业园区格网信息科技有限公司,苏州 215027
2)江苏CORS 苏州分中心,苏州 215027
3)四川省第一测绘工程院,成都610100
1 引言
为提高GPS 定位精度及可靠性,在利用GPS 定位时,要探测和修复GPS 载波相位的周跳。探测周跳的方法有多种[1-6],如多项式拟合法、高次差法、电离层残差法等,基于移动窗口的抗差Chebyshev多项式的拟合探测[1]、基于抗差Chebyshev 多项式的相位伪距探测等。
本文采用这些方法对GPS 参考站数据进行周跳探测,结果其中某个GPS 参考站数据的周跳探测结果出现了矛盾,经过分析,发现该参考站数据的观测时刻与记录时刻不一致,针对该问题,提出了两种解决方法。
2 问题的发现与证明
2.1 问题的发现
对SCIGN 网中VTIS 参考站2012年7月18日的观测数据进行周跳探测,采用不同的方法得到的结果互相矛盾,经过分析发现是在该接收机Rinex观测文件中,观测数据的记录时间(2012.07.18 00:23:30)与观测时间(00:23:29.999,两者相差1 ms)不一致,导致计算与观测的有关数据发生错误,在采用以观测间隔为参数的多项式拟合法和高次差法探测周跳时,使模糊度固定错误。
如图1,选取SCIGN 网中的4 个参考站WMAP、PSDM、WRHS、VTIS,构成6 条基线。对6 条基线进行计算,发现含有VTIS 站的基线存在异常。
以WMAP-VTIS 基线为例,采用抗差Chebyshev多项式探测周跳,发现第95 个历元所有观测的双差相位观测值均发生周跳,采用高次差法与常规多项式法进行周跳探测,周跳同样存在(图2)。
以G04-02 双差卫星为例,采用WM 组合观测值求宽巷模糊度并进行滤波,其结果见图3。
由图3 可见,WM 组合观测值未发现周跳。按卡尔曼滤波方式求得的滤波解见图4。从图4可以看出,Δ▽N1在95 历元处发生了跳变,说明之前的周跳修复有误,周跳探测结果存在错误。

图1 参考站分布图Fig.1 Distribution of reference stations
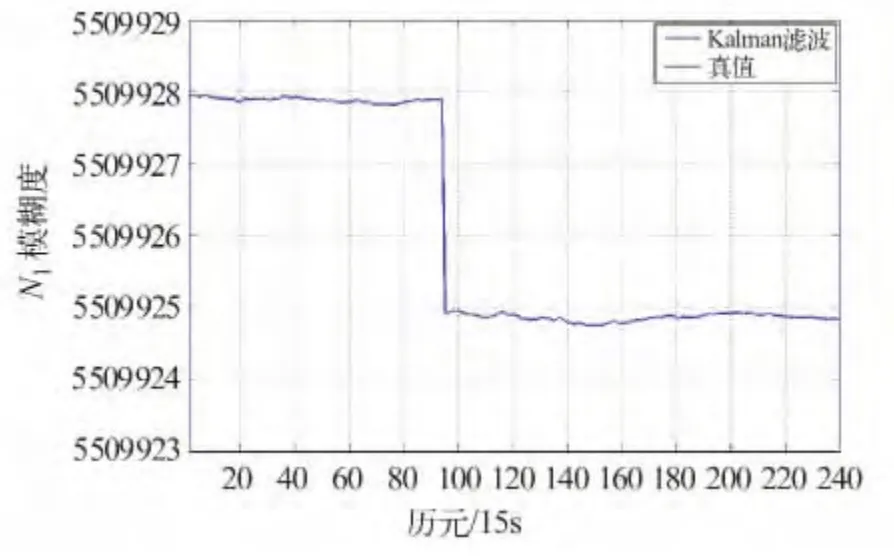
图2 周跳探测结果Fig.2 Results of cycle slip detection
图5是利用观测值直接计算的每个历元的Δ▽N1。由图5 可以看出,在第95 个历元处存在-3 周的周跳,这与之前修复的-3 周周跳数值一样,说明第95 历元处的观测数据可能不存在周跳,而错误地进行了-3 周的修复。
再利用电离层残差法对第95 历元附近数据进行周跳探测,结果见表1。从表1 可以看出,各差值均小于阈值0.07,表明第95 历元没有发生周跳。
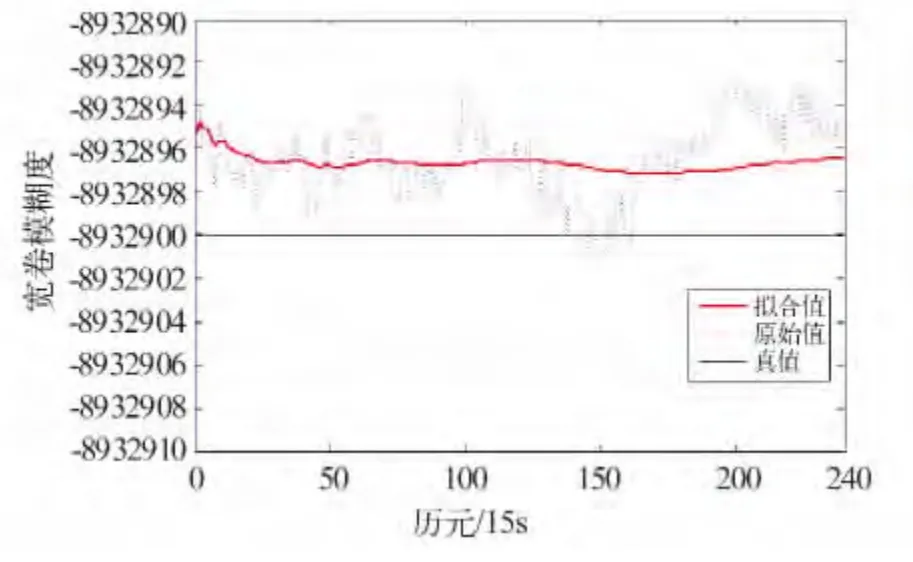
图3 利用WM 组合(真实站星距)求得的宽巷模糊度Fig.3 Ambiguity of wide lane got by WM combination(real station distance)
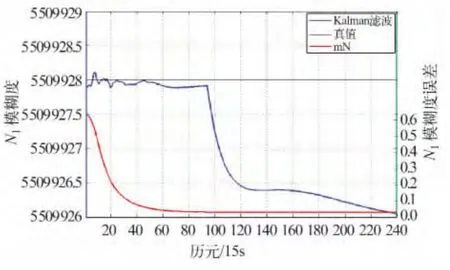
图4 卡尔曼滤波求取的Δ▽N1Fig.4 Δ▽N1 by Kalman filter
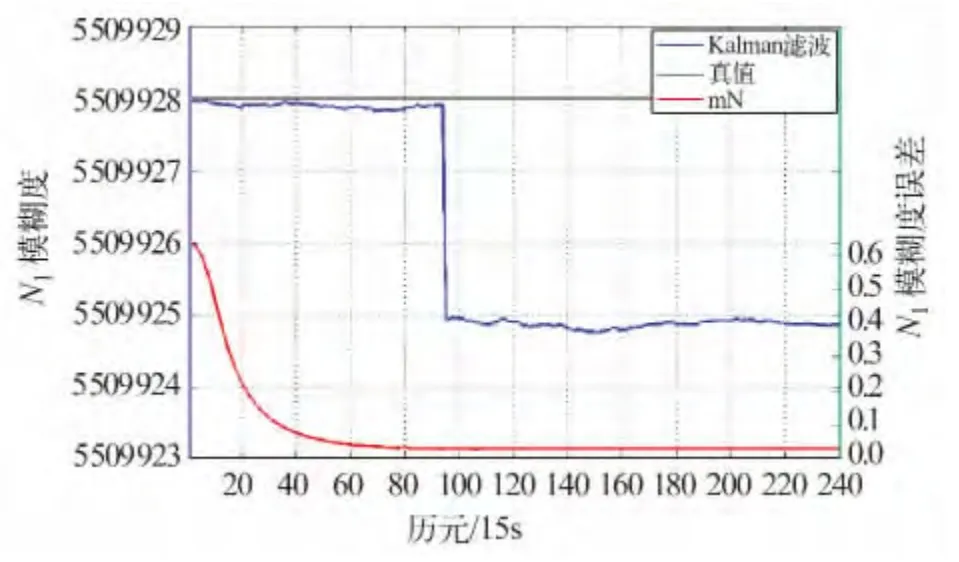
图5 直接计算得到的Δ▽N1Fig.5 Δ▽N1 by observation data
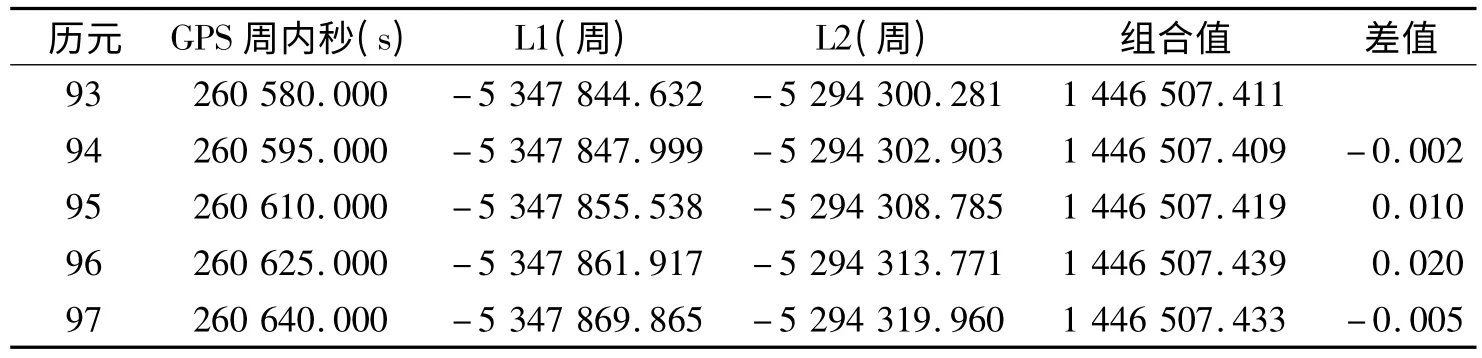
表1 电离层残差法周跳探测结果Tab.1 Cycle slip detection results with ionosphere residual method
对原始观测数据不进行周跳修复直接进行宽巷模糊度固定并分解Δ▽N1,结果如图6。从图6 可以看出,Δ▽N1的滤波过程很平稳,固定于5 509 928。
根据计算与分析,可以认为原始数据中不含周跳,采用与时间相关的抗差多项式法和高次差法进行周跳探测,探测结果是错误的。
为验证抗差多项式法和高次差法探测周跳的能力,在第51 历元处L1的双差相位观测值上人为地加入1 周的周跳,再进行周跳探测实验,周跳得到了准确的发现,修复后得到与图6 一致的固定的Δ▽N1。如果不加以修复,其结果见图7。实验表明,抗差多项式法和高次差法探测双差观测值周跳的能力为1 周,与文献[1]中的结论一致。说明这两种探测方法本身没有问题。

图6 正确固定Δ▽N1Fig.6 Correct fixed Δ▽N1

图7 加入1 周周跳而不进行修复得到的Δ▽N1Fig.7 The Δ▽N1 with 1 cycle slip
由于得出VTIS 参考站接收机的真实观测间隔与所设置的固定观测间隔不一致,使得抗差多项式法和高次差法无法获得正确的周跳探测结果。
2.2 证明
每个历元卫星信号的发生时刻为
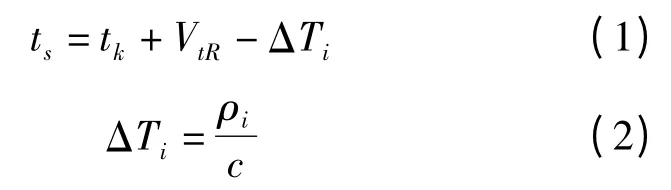
式中tk为记录时间,VtR为观测时刻接收机钟差改正数,ΔTi为信号从卫星i 传播至接收机所需的时间。
由于计算卫星位置时需要用到卫星信号的发生时刻ts,而计算ts又需要用到卫星位置ρi(ρi根据卫星坐标和测站坐标反算),所以需要进行迭代计算。
虽然观测文件中的记录时间tk可能有误,但Rinex 观测文件中的记录时间起到计算信号发射初始值的作用,在多次迭代中便会得到真实的卫星信号发射时刻,与记录时间的微小偏差量无关。由于卫星在一段时间内的运行轨迹的变化比较平缓,且观测是等采样率的,那么卫星发射时刻的时间差约等于采样间隔,如果哪个历元卫星信号发射时刻的间隔发生了跳变,就说明该历元的实际观测时间和观测文件中记录的整数秒时间存在差异。现计算G04 号卫星第81—100 个历元的信号发射时刻间隔,结果见表2。
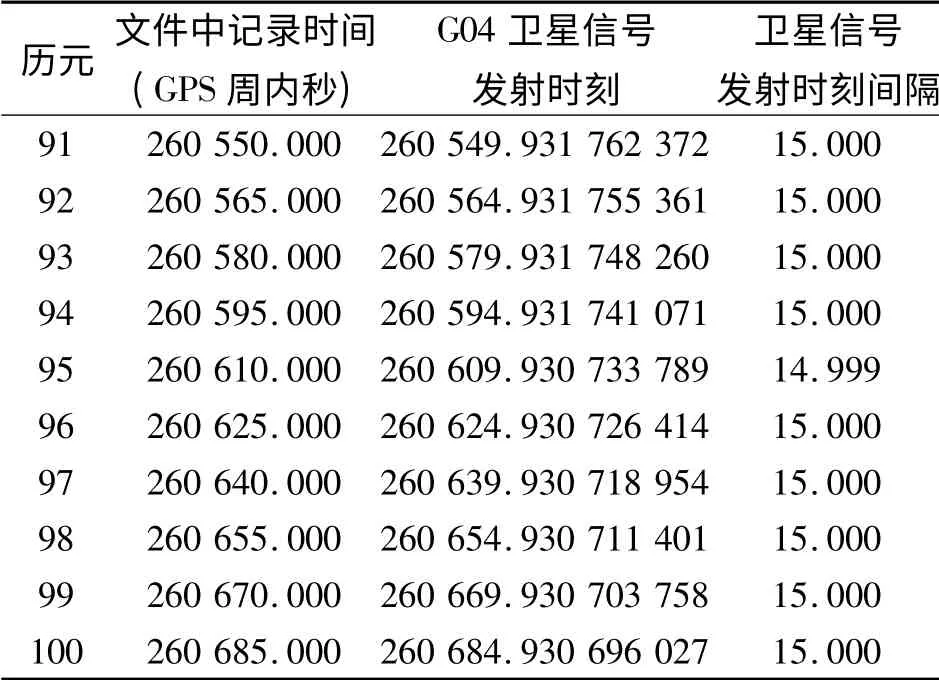
表2 G04 卫星信号发射时间间隔表(单位:s)Tab.2 Signal emission interval of satellite G04(unit:s)
由表2 可见,第95 历元信号发射时刻的间隔发生了1 ms 的跳变。所以,第95 个历元的实际观测时刻为120 718 002 329.999,且后面历元的真正观测时间均应在记录的时间上减掉1 ms。由于GPS参考站是连续观测的,会不断更换双差参考星,因此只有在包含跳变时刻的计算时段内才会出现异常。
3 解决方法
3.1 方法1
利用多种方法进行组合探测。表2表明,记录时间与观测时间相差1 ms,造成约4 周的假周跳,在利用多项式等方法探测时,设置探测的最小周跳为4 周,再利用电离层残差法探测小于4 周的周跳。采用该方法对实验数据再次进行计算,得到Δ▽N1的计算结果如图8。可以看出,图8 和图6是一致的,表明组合周跳探测的结果是正确的。
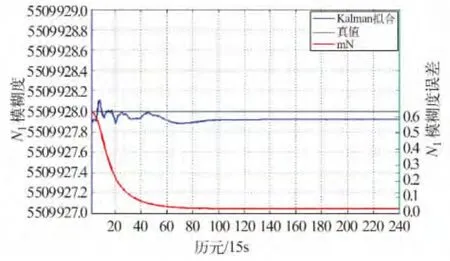
图8 经方案1 正确固定的Δ▽N1Fig.8 Correct fixed Δ▽N1 by method 1
采用方法1 如果遇到两种时刻不一致时,需要设置多大的周跳值,则需要综合多种方法进行探测。
3.2 方法2
在数据预处理时对每个历元的信号发射时刻进行计算,检查是否出现跳变,如果出现跳变,则对Rinex 观测文件中的观测时刻进行整ms 数的修正。
对实验数据进行探测后发现在95 历元处存在跳变。计算结果见表3。

表3 修正后的观测时间表(单位:s)Tab.3 The adjusted observation schedule(unit:s)
利用修正后的时间再采用抗差多项式法计算Δ▽N1,其结果如图9。可以看出,图9 与图6 一致,表明经过修复后得到的实际观测时间是正确的。
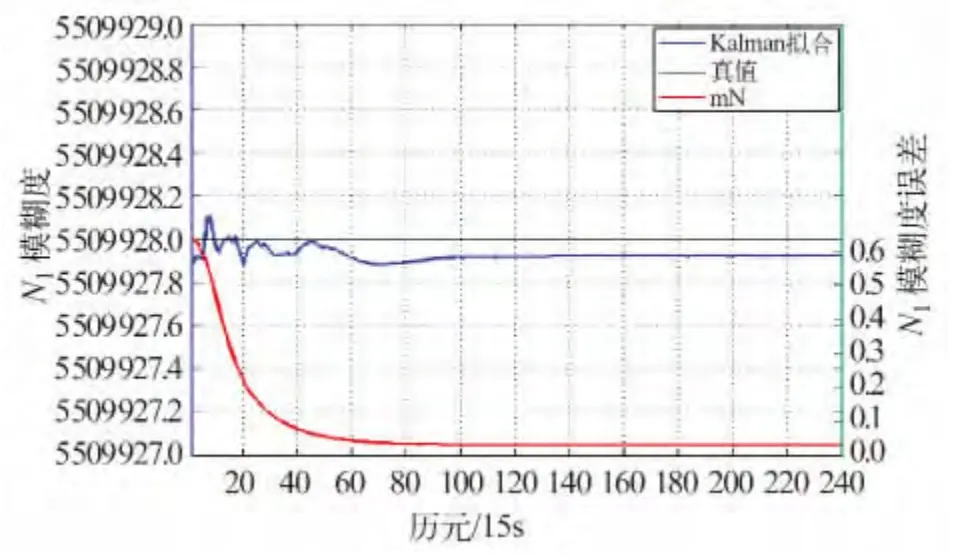
图9 经方法2 修正后的Δ▽N1Fig.9 Correct fixed Δ▽N1 by method 2
4 结论
1)当接收机观测值的记录时间与观测时间不一致时,采用与时间相关的周跳探测方法会使探测结果产生错误,严重时将导致模糊度固定失败和定位错误;
2)GPS 周跳探测不能只采用一种类型的方法,需采用多种类型的组合探测法,确保周跳探测结果的可靠性;
3)建议使用第2 种方法对观测数据进行预处理,以便发现并解决问题。
1 刘宁,熊永良,徐韶光.基于移动窗口的抗差Chebyshev多项式拟合探测与修复单频GPS 周跳[J].大地测量与地球动力学,2011,(2):94-98.(Liu Ning,Xiong Yongliang and Xu Shaoguang.Cycle slip detection and correction for single-frequency GPS data based on sliding window of Chebyshev polynomial fitting of robest estimation[J].Journal of Geodesy and Geodynamics,2011,(2):94-98)
2 王建,张献州,李伟.基于抗差Chebyshev 多项式的相位伪距周跳探测与修复算法[J].测绘与空间地理信息,2012,(9):26-28.(Wang Jian,Zhang Xianzhou and Li Wei.Cycle slip detection and correction based on Chebyshev polynomial of robust estimation[J].Geomatics & Spatial Information Technology,2012,(9):26-28)
3 李明,高星伟,徐爱功.一种改进的周跳多项式拟合方法[J].测绘科学,2008,(4):82-83,99.(Li Ming,Gao Xingwei and Xu Aigong.A modified polynomial fitting for cycle-slip processing[J].Science of Surveying and Mapping,2008,(4):82-83,99)
4 石双忠,冯尊德.利用多项式拟合预测残差修正法估算周跳值[J].测绘科学,2013,(1):33-35.(Shi Shuangzhong and Feng Zunde.Estimation of GPS carrier cycle slips value using correction of residuals predicted by polynomial fitting[J].Science of Surveying and Mapping,2013,(1):33-35)
5 蔡诗响,等.一种基于多项式拟合的单频周跳探测改进方法[J].测绘信息与工程,2009,34(5):1-3.(Cai Shixiang,et al.A modified method for cycle slip detection based on polynomial fitting[J].Journal of Geomatics,2009,34(5):1-3)
6 罗峰,姚宜斌,宋伟伟.综合利用多项式拟合和载波相位变化率探测单频GPS 周跳[J].全球定位系统,2007,(05):9-13.(Luo Feng,Yao Yi bin and Song Weiwei.Detecting cycle slip using polynomial fitting and carrier phase rate method[J].GNSS Word of CHina,2007,(5):9-13)
7 杨剑,等.GPS 接收机钟跳研究[J].大地测量与地球动力学,2007,(3):123-127.(Yang Jian,et al.On clock jumps of GPS receiver[J].Journal of Geodesy and Geodynamics,2007,(3):123-127)
8 熊永良,等.虚拟参考站技术中对流层误差建模方法研究[J].测绘学报,2006,(2):118-121,132.(Xiong Yongliang,et al.Study on modeling tropospheric delay in virtual reference station[J].Acta Geodaetica et Cartographica Sinica,2006,(2):118-121,132)
