基于时间序列的GPS 速率可靠性分析*

丁晓光 甘卫军 肖根如 张 艺

1)地震动力学国家重点实验室，中国地震局地质研究所，北京 100029

2)陕西省地震局，西安 710068

3)东华理工大学，抚州344000

1 引言

中国地壳运动观测网络”(简称“网络工程”)［1］和“中国大陆构造环境监测网络”(简称“陆态网络”)［2］的GPS 观测站既有长年不间断连续观测的基准站，也有每隔1 ～2年临时连续观测3 ～4天的流动站。截至2013年，网络工程的27 个GPS 基准站已积累了约14年跨度的连续观测数据，1 055 个流动站至少已有7 ～8 期的重复观测;而陆态网络建成于2012年，233 个新建连续站仅有2 ～3年的观测时长，1 000 个新建流动站只有2009年和2011年两期观测。由于两个项目的GPS 观测时间跨度和重复观测期次相差悬殊，那么基于时间跨度较短的连续GPS 观测和非连续GPS 观测所得到的站点速度可靠性如何?该问题也即，要获取可靠有效的GPS 站点速度，连续站需要累积多长时间的观测，流动站需要几期的观测和多长的时间跨度?针对这个疑问，本文将以“网络工程”基准站长时间跨度的连续GPS 观测数据和速度结果为基础，采用模拟观测(数据分段模拟连续观测，以及随机抽取连续数据模拟流动观测)和数值计算方法给出了全面的统计分析。

2 连续GPS 数据及数据处理

利用GIPSY-OASIS(Ver.6.0)软件［3，4］精密单点定位模式对“网络工程”站点1999—2012年的观测数据进行计算，获得单日松弛约束解，然后采用联合平差软件QOCA［5］对所有站点的单日松弛约束解严密平差，获得各站点的坐标变化序列。数据处理中具体要点为:以消除电离层影响的线性组合作为观测量，卫星截止高度角为15°，应用JPL 精密星历和时钟产品并估计钟差参数;先验对流层延迟模型采用全球大气压温度模型(GPT，Global Pressure and Temperature)，投影函数为GMF，再用参数估计对流层延迟剩余部分;海洋潮汐改正由FES2004 模型基于格林函数在线计算获得;进行接收机天线和卫星天线绝对相位中心改正;采用Ambizap 模块进行整周模糊度解算［6］，该模块的处理算法是利用固定点法则来确定观测网参数的各种线性组合，并为整个观测网生成消除整周模糊度且唯一、自洽的单日解;最后利用QOCA 软件与全球271 个IGS 站的单日松弛约束解进行联合平差，通过选取的IGS 站进行7参数变换将单日解统一转换到ITRF2008 框架下。

从解算得到的各站点时间序列中选取数据较为完整、结果较为稳定的XNIN(西宁)站作为实验对象。通过QOCA 软件analys_timseri 模块对原始时间序列进行分析，删除个别偏离线性过大的突跳点，去除2001年11月14日昆仑山地震的同震影响，以及其他几次由于更换天线造成的大幅阶跃(图1)。为便于后续研究，截取了时序年变稳定的一段数据进行分析(2001年年积日100天至2010年年积日220天)，利用最小二乘算法求得该段数据N、E、U分量的年平均速率分别为:－3.80 mm/a、37.94 mm/a 和0.02 mm/a。

3 GPS 速率模拟计算与可靠性分析

3.1 连续站速率可靠性分析

为研究获得稳定可靠的速率所需最短观测时长，采用了以下计算方法:以第1天至360天数据得到的速率值为起始点，每增加1天，重新计算一次速率，这样便得到了361，362，…直至全部数据得到的速率，将其连成一条曲线，当曲线波动小于给定阈值时，即表示速率值稳定。再以第10天至370天的速率为起始点，重复以上计算，又会得到一条曲线…以此类推，分析起算时间位于坐标序列不同相位时的速率变化。

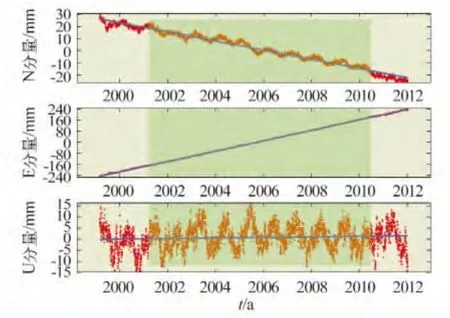
图1 XNIN 站坐标时间序列Fig.1 Coordinate time series of XNIN station

利用QOCA 软件时序分析模块计算XNIN 站时间序列N、E、U 分量的周年项相位，分别为347.83°、224.39°、316.76°，与田云锋［7］计算结果(351.69°、215.15°、337.68°)基本相同。由此推算N 方向的0 相位处于每年年初10 ～15天。图2 为N 分量起算速率的相位大致位于0°、90°、180°、270°时的速率变化曲线。

从图2 来看，水平分量速率曲线均呈现振幅递减的波动状态，振幅约1 ～3 mm，在持续3 ～4年后，波动变化小于0.5 mm，速率趋于稳定;在不同初始相位时，各曲线变化趋势各不相同，N 分量变化范围在－1 ～－5 mm 之间，E 分量则达到35 ～41 mm。垂向分量由于振幅较大，而线性速率很小，故拟合速率呈直线变化，受突跳点影响出现毛刺，未得到可用于分析的结果。

速率曲线上下波动逐渐趋近于稳定值，这一现象说明，在计算所用数据量不能使速率稳定之前，增加观测天数未必能得到更真实的速率值;要获得稳定可靠的结果需3 ～4年的观测时长。值得指出的是，高精度GPS 软件在处理长时间观测数据时，除对测站坐标线性拟合出速率外，还要在稳定参考框架下进行。与已知准确速率的测站组绑定一起平差，能够在相对较短的时间内得到稳定的速率，这与本文讨论的利用时间序列拟合获得速率的方法有很大不同，关于流动站速率的可靠性的分析与之类似。

3.2 流动站速率可靠性分析

首先对XNIN 站时间序列中所有坐标点进行加权滑动平均，滑动窗口为4天。对原坐标序列所有数据进行滑动平均后，得到了新的“流动GPS”坐标时间序列(简称“新序列”)，每一时间点均对应4天流动测量。

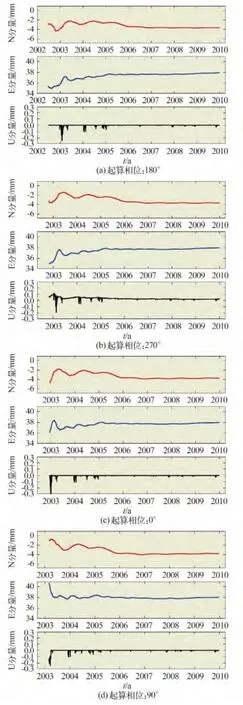
图2 以N 分量坐标序列不同相位起算得到的速率曲线Fig.2 The rate curves calculated by different phases of coordinate series of component N

以新序列中第1 组数据为一期观测，间隔N年后再选1 组数据作为第二期观测，每期观测时间点的选取方法为:

Δt 为在1 至100 间随机抽取的整数，模拟每期观测时间相差的天数。在自动选取得到多期数据之后，拟合获得第一组速率值。然后再以新序列中第2 组数据为第一期观测，按照同样方法选取多期模拟观测值，拟合得到第二组速率值…以此类推，可以得到多组速率值，约定每组速率值与各自第一期的观测时间形成对应关系，构成一条速率-时间曲线。

根据每期观测时间间隔和总时长的不同，设计了三种流动模拟观测方案。

方案一:每1年观测1 期。观测总时长为3、4、5、6、7 期;

方案二:每2年观测1 期。观测总时长为2、3、4 期;

方案三:每3年观测1 期。观测总时长为2、3期。

每种方案都计算了新序列的前720 组数据，从而得到720 个速率结果组成的序列。将各方案得到的速率序列与拟合的连续站速率相比较，计算其差异的标准差，作为外符合精度;再与本速率序列的平均值比较，计算差异的标准差作为内符合精度(表1)。

由表1 可见，在观测周期相同时，随观测期数的不断增加，内、外符合精度均不断减小;在时间跨度相同时，观测期数不同，得到的内、外符合精度基本相当(图3 ～5)。

根据图3 ～5 并结合表1，3 种方案得到的速率可靠性相近，当然前提是每期观测数据质量都能得到保证，实际上，增加观测期数来提高结果的可信度是必要的，如每期测量时采用不同型号天线、天线高量测、拆装整平天线等都会影响解算结果。由图3 ～5 还可以看出，在速率曲线的三个分量上均存在年周期变化，并且波动幅度随时间跨度的增长而减小。

结合表1 所列数据，虽然在时间跨度达到5 ～6年时，速率序列的水平分量标准差提高到0.5 mm左右，垂向标准差约为1 mm，但真实的流动测量只可能得到序列中的某一个速率值，由于年周期变化的存在，其计算结果会大于标准差。为了对流动观测速率可靠性有完整的认识，表2 列出了各方案速率序列与已知的连续站速率做差后，差异值的变化范围。

表1 各方案得到的速率序列的标准差(单位:mm/a)Tab.1 Standard deviations of rate series calculated by different schemes(unit:mm/a)

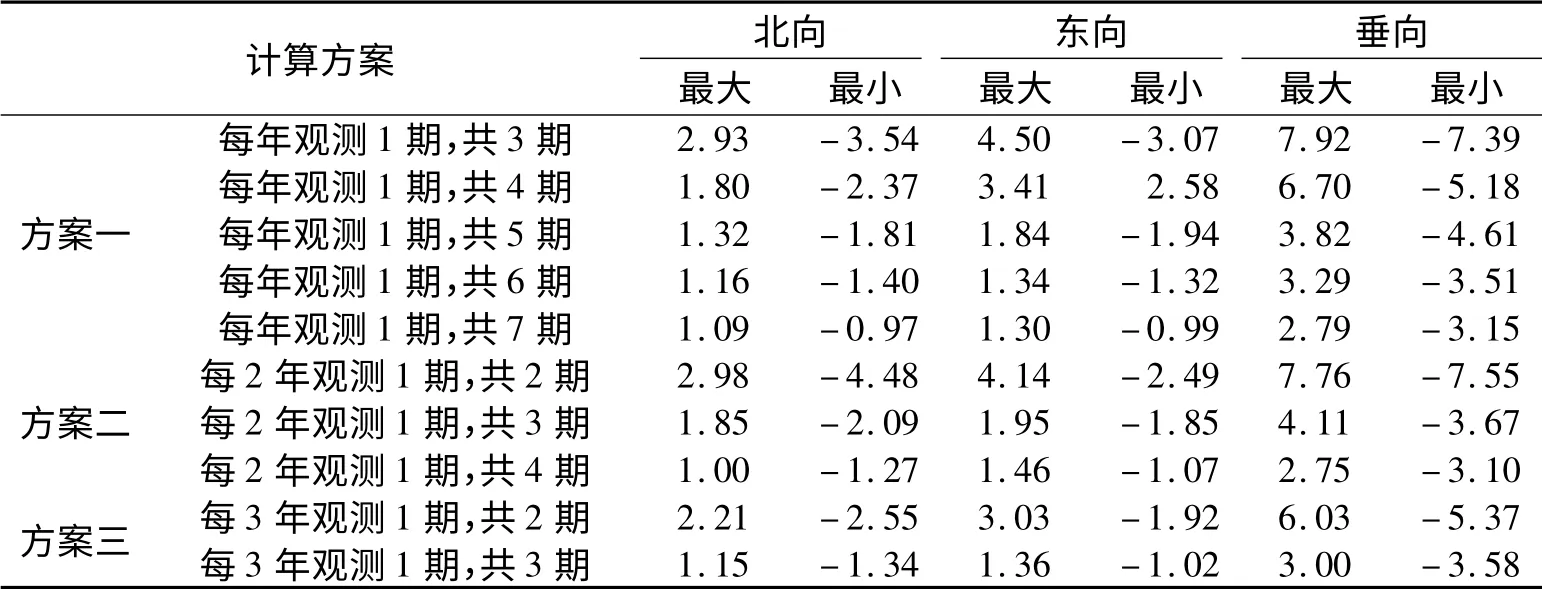
表2 各方案得到的速率序列与连续站速率值的差异(单位:mm/a)Tab.2 Differences between the rates calculated by different schemes and the rates directly fitted the data of continuous station(unit:mm/a)

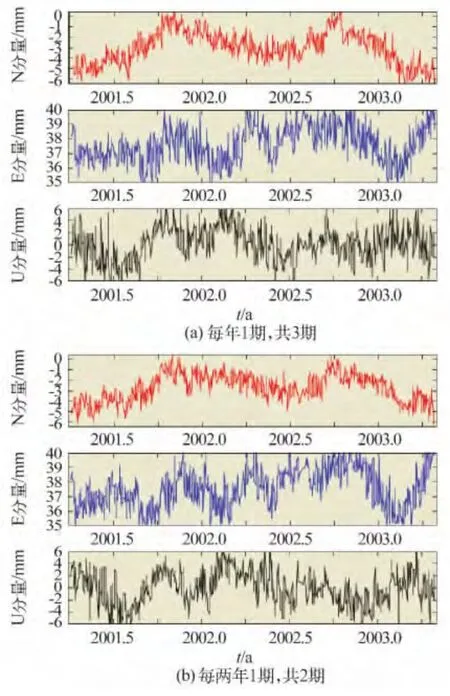
图3 时间跨度为两年的速率曲线比较Fig.3 Comparation of the velocity curves in 2 years

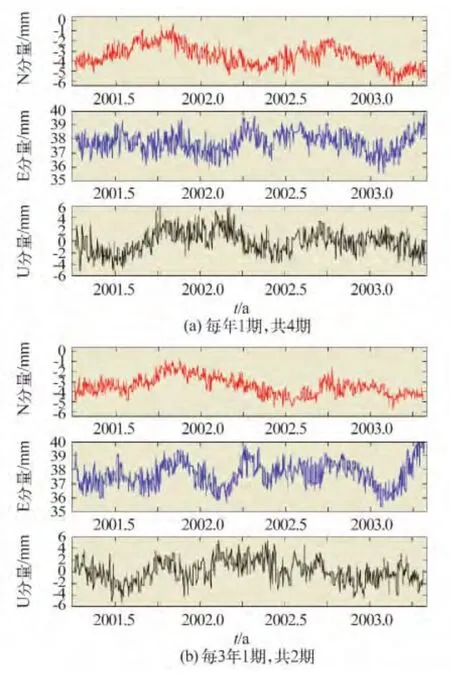
图4 时间跨度为3年的速率曲线比较Fig.4 Comparation of the rate curves in 3 years

式中x0为起算数据，v 为拟合线性项(速率)，Si、Ci为时间序列谐波分量振幅，主要为周年和半年项周期变化。Hk为第k 次阶跃，Bk表示该次阶跃对后续时间序列影响的函数，Rj为剩余的残差项。

同样XNIN 站的时间序列为例，扣除阶跃和强震影响，不考虑第四项;则周期项可以表示为振幅和相位的函数，即Aisin(ωit + φi)。其中，振幅Ai=，相位

流动观测中两期观测时刻分别为ti和tj，相应坐标为x(ti)和x(tj)，则速度

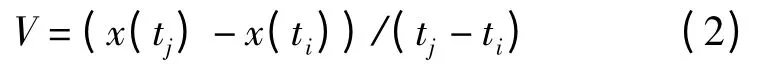
将式(1)代入式(2)，令ti=0，考虑同一序列不同时刻振幅频率相等，得

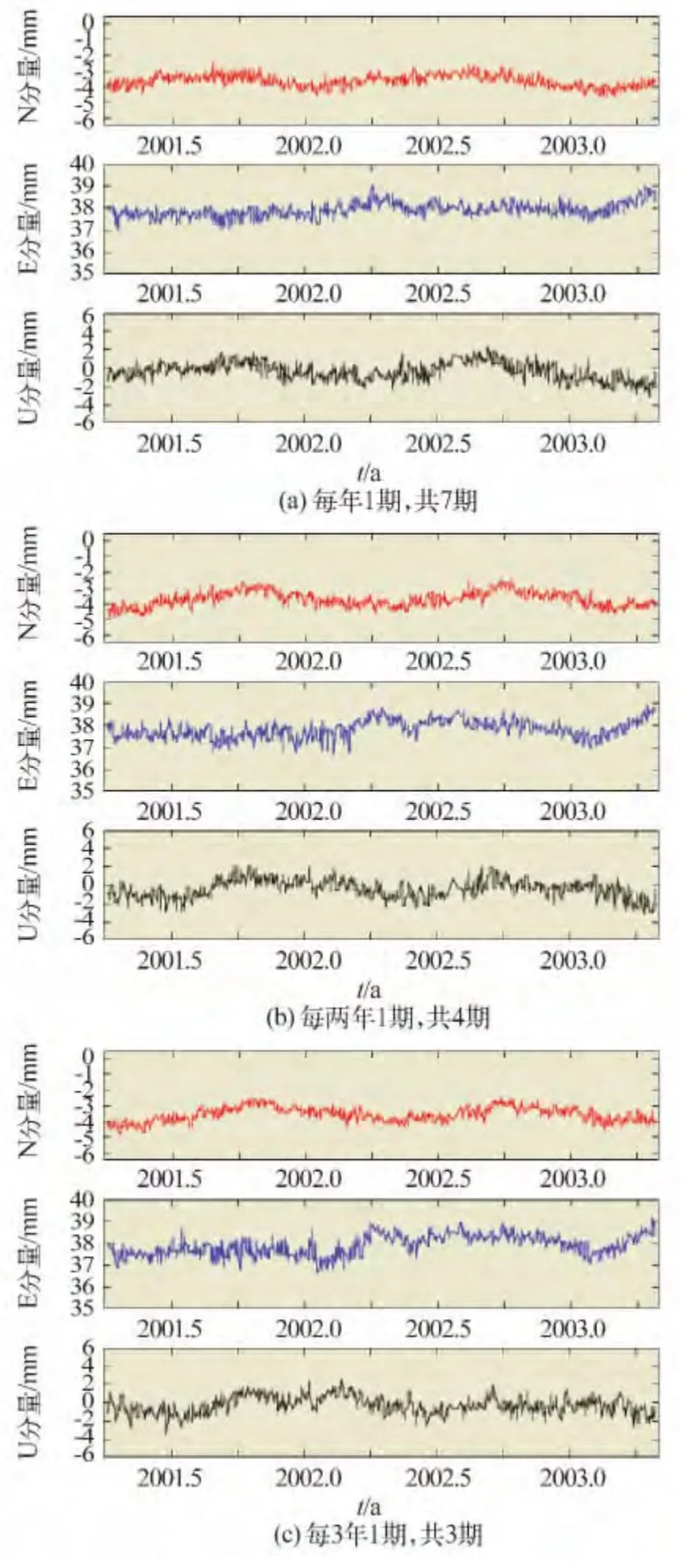
图5 时间跨度为6年的速率曲线比较Fig.5 Comparation of the velocity curves in 6 years

从表2 中可以看到，当时间跨度仅为2年时，得到的流动站速率与真实值的偏差在水平方向可以达到±3 ～4 mm/a，而垂向分量的速率波动接近±8 mm/a;当时间跨度为4年时，水平方向速率的可靠性在±3 mm/a 以内，垂向分量的波动水平在±5 mm/a 以内;即使时间跨度达到6年，水平速率仍可能有超过±1 mm/a 的偏差，垂向的偏差则可能有±3 mm/a。如果再考虑实际观测时的复杂影响因素，流动GPS 速率的可靠性还要降低。

4 速率可靠性的影响因素与讨论

时间序列中任意时刻t 点均可表示为

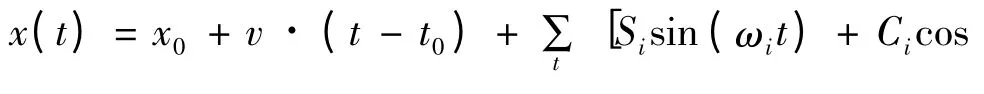
当初始相位φi已知时，第二项为正弦函数。由式(3)可知，流动观测中影响速率估计的因素有相位差、振幅和残差，其中相位差由两期观测的时间差异决定;振幅取决于站点固有频率周期;而残差则决定于站点观测噪声的大小，它们都能够随观测间隔t的增加而减少;在相同时间间隔内加密观测期数能够提高速率v 的拟合精度，却无法消除周期误差和残差的影响，速率的准确性未得到有效提高，例如本文中利用连续站(相当于每天1 期流动观测)得到的水平速率结果，在观测时长为3年时仍有1 mm左右波动，直到时长为4 ～5年时速率值才趋于稳定。当然，根据连续站时间序列估计周期项参数和噪声类型，可以缩短获得可靠速率值所用时间，但是要得到较为准确的周期和噪声模型，也至少需3年有效观测。

与连续站相比，流动站仅靠自身每期数天观测无法获知周期振幅和残差模型，此时只有通过缩小两期观测时间差异、增加观测时间跨度来提高速率结果的可靠性。另外，随着连续站布设密度的逐步提高，流动站的周期性变化模型可以由邻近连续站拟合近似得出，从而达到改善流动站速率可靠性的目的。

5 结论

1)针对XNIN 连续站，通过拟合时间序列获得的站点速率，需要至少3 ～4年数据累积才能获得稳定可靠的结果(＜±0.5 mm/a)。当数据积累时间较短时，计算速率的起始点位于时间序列的不同相位，会引起不同的速率变化趋势。

2)利用XNIN 连续站模拟的流动观测，当时间跨度为2年时，速率的水平分量波动范围可达±3 ～4 mm/a;时间跨度达到6年时，速率水平分量可靠性接近±1 mm/a，垂向分量约为±3 mm/a。如果考虑实际观测时每期仪器更换等因素影响，可靠性还要低于估计值。

3)对于所有连续站和流动站，获得稳定可靠的速率所需时间长短受站点固有周期和噪声水平影响。

4)增加观测时间跨度，缩小流动观测两期观测时间差异可以提高速率结果的可靠性。

1 甘卫军，等.中国地壳运动观测网络的建设及应用［J］.国际地震动态，2007，343(7):43－52.(Gan weijun，et al.Construction and application of crust movement observation network in China Continant［J］.Development of Internanional Earthquake，2007，343(7):43－52)

2 甘卫军，等.中国大陆构造环境监测网络的建设与应用［J］.工程研究，2012，4(4):324－331.(Gan Weijun，et al.Construction and application of tectonic environment observation network in China Continant［J］.Engineering Studies，2012，4(4):324－331)

3 肖根如，甘卫军，殷海涛.GIPSY 软件的GPS 数据处理策略及应用［J］.地球物理学进展，2010，25(4):1 508－1 515.(Xiao Genru，Gan Weijun and Yin Haitao.GPS data process strategies and application of GIPSY software［J］.Progress in Geophys，2010，25(4):1 508－1 515)

4 Gregorius T.GIPSY-OASIS II:How it Works，(self-published)，Univ.of Newcastle upon Tyne，Newcastle，England，U.k.，1996.

5 Dong Danan，Herring T A and King R W.Estimating regional deformation from a combination of space and terrestrical geodetic data［J］.J Geodesy.，1998，72:200－214.

6 Geoffrey Blewitt.Fixed point theorems of GPS carrier phase ambiguity resolution and their application to massive network processing:Ambizap［J］.Journal of Geophysical Reasearch.2008，113，B12410.

7 田云锋.GPS 位置时间序列中的中长期误差研究［D］.中国地震局地质研究所，2011.(Tian Yunfeng.Study on intermediate-and long-term errors in GPS position time series［D］.Institute of Geology，CEA，2011)

8 占伟，等.GNSS 流动观测水平速度精度评估［J］.大地测量与地球动力学，2011，(5):84－87.(Zhan Wei，et al.Accuracy evaluation of horizontal velocity in GNSS mobile observation［J］.Journal of Geodesy and Geodynamics，2011，(5):84－87)

9 王敏，等.非构造形变对GPS 连续站位置时间序列的影响和修正［J］.地球物理学报，2005，48(5):1 045－1 052.(Wang Min，et al.Effects of non-tectonic crustal deformation on continuous GPS position time series and correction［J］.Chinese J Geophys.，2005，48(5):1 045－1 052)