PMSM矢量控制在雕铣机进给系统中的实现*
2014-02-11王小东王天雷
王小东,王天雷
(1.广东科杰机械自动化有限公司,广东江门 529030;2.五邑大学信息工程学院,广东江门 529020)
PMSM矢量控制在雕铣机进给系统中的实现*
王小东1,王天雷2
(1.广东科杰机械自动化有限公司,广东江门 529030;2.五邑大学信息工程学院,广东江门 529020)
永磁同步交流伺服电机(PMSM)是数控雕铣机进给系统中的一个关键部件,其控制方法对伺服系统的性能起重要作用。建立了该类电机的数学模型并研究了矢量控制原理,并采用DSP控制器实现了伺服电机的电流、速度双闭环控制系统并测试了该控制系统下电机的转速、电流及转角。最后对比了运动控制仿真结果与实验结果,验证了该控制方法的可行性和准确性,为该类电机的控制以及在数控机床上的应用提供了理论依据。
永磁同步伺服电机;矢量控制;CCS
雕铣机(CNC engraving and milling machine)既可以雕刻,也可铣削,是一种高效高精的数控机床,广泛应用于精密模具粗精加工一次完成,紫铜电极,铝件产品批量加工,鞋模制造,钟表眼镜行业等。雕铣机性价比高,加工速度快,加工产品光洁度好,在机床加工业越来越占有重要地位。为保证雕铣机的加工精度,应包含的特性有:自动化程度高、加工精度高以及稳定性好。在雕铣机中进给伺服系统的控制性能决定了雕铣机的加工性能,因此,在雕铣机进给系统中的永磁同步伺服电机控制方法的选择与实现会影响整个加工精度[1]。
电机的矢量控制是目前应用广泛的控制方法。近几年来,国内外学者将空间矢量PWM控制技术应用于永磁同步电机控制中,并取得了相当的成就。同时,随着对PMSM控制技术要求的提高,矢量PWM控制系统成为首选控制方案[2]。为此提出一种控制性能良好的永磁同步伺服电机矢量控制系统,并对永磁同步电机数学模型和矢量控制原理做了相关的研究,搭建了永磁同步电机矢量控制模型并对其进行了编程仿真研究。
1 永磁同步电机的数学模型
为了实现对永磁同步电机控制,需要先对其建立良好的数学模型。在DSP控制系统中采用d-q坐标系下的数学模型,因为这是矢量控制原理的根本。数学模型建立过程如下。
1.1 永磁同步电机a-b-c坐标系的建立
首先建立a-b-c坐标系下的数学模型见式(1):
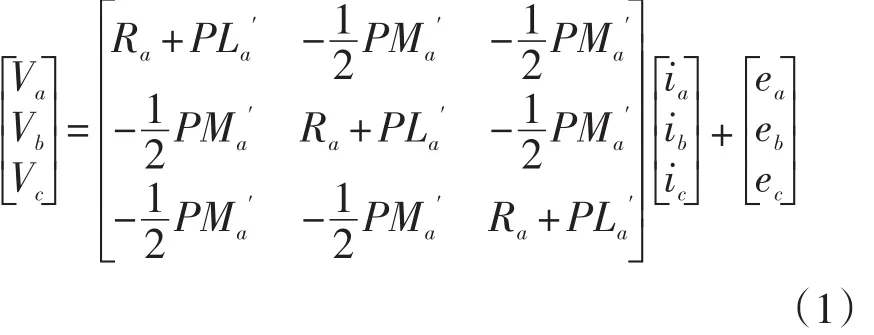
其中:Va,Vb,Vc为a,b,c相电枢电压(V);ia,ib,ic分别为a,b,c相电枢电流(A);ea,eb,ec为由永磁体磁场分别在a,b,c相电枢中引起的电势;Ra为电枢绕组电阻(Ω);La′为电枢绕组的自感(H);Ma′为电枢绕组间的互感(H);P为微分因子(d/dt)。
1.2 d-q坐标系下的数学模型
设两相同步旋转坐标系的d轴与三相静止坐标系的u轴的夹角为θ,则从三相静止坐标系u-v-w到两相旋转坐标系d-q的变换矩阵见式(2):
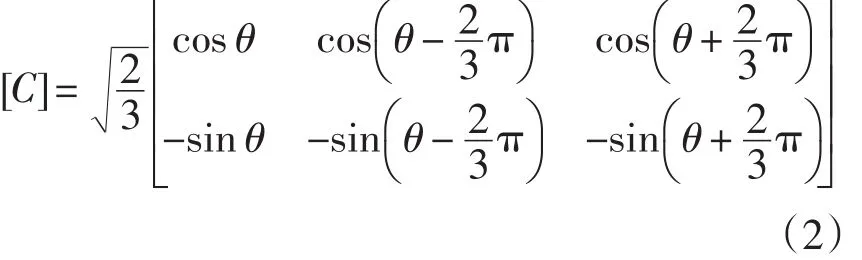
在保证电机的磁势和功率不变的情况下,利用Clarke和Park变换,把式(1)电压方程变换到d-q坐标系下,即可得到电枢电压和电枢电流都是直流量的永磁同步电机的电压方程式[3]。d-q坐标系下的电压方程如式(3)所示:
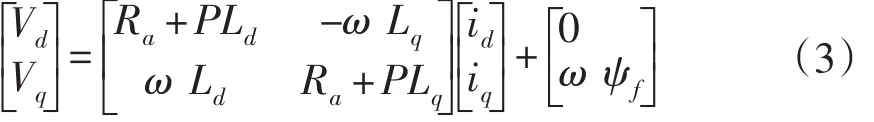
其中 Vd,Vq为d-q轴电枢电压(V);ω为旋转角速度;id,iq为d-q轴电枢电流(A);Ld,Lq为d-q轴定子绕组自感。
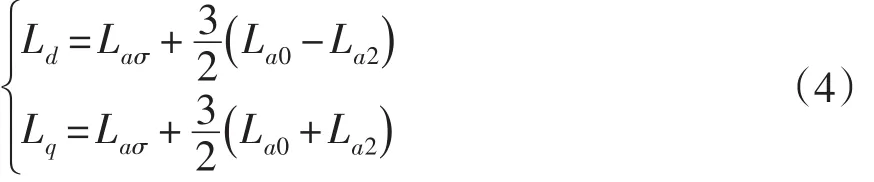
式(4)中: Laσ为定子绕组的漏感; La0为定子绕组自感的平均值;La2为定子绕组自感的二次谐波幅值。
因此转子永磁体产生的主磁通在d轴绕组中引起的反电势为0,而在q轴绕组中引起的反电势是 ωψf,这是因为转子只有d轴方向的磁通,而没有q轴方向磁通的原因[4]。
2 永磁交流伺服电机的矢量控制系统
直流电机的控制方式比较简单,这是由其模型所决定。励磁磁场由励磁电流产生,电枢磁场由电枢电流产生,可分开控制而不会相互影响。而永磁同步电机的模型复杂,非线性而且各个量之间相互耦合,永磁体产生的磁场和定子绕组产生的磁场是不垂直的。因此,要通过矢量控制的方式经坐标变化来建立虚拟的坐标系使得两者相互垂直,这也正是矢量控制的本质意义所在[5]。
2.1 矢量控制的基本原理
从永磁同步伺服电机的数学模型可以看出,对电机输出转矩的控制最终归结为对其交、直轴电流的控制。对永磁交流同步电机的矢量控制的方法主要有:id=0控制、最大转矩控制、弱磁控制以及控制等,该矢量控制的方法的提出是对电机控制领域的一个巨大的创新。该控制方法是将定子电流分解成产生磁场的部分和产生转矩的部分,分解后,模拟直流电机的控制方法,对这两个组件可以单独控制[6]。矢量控制坐标变换结构框图见图1所示。
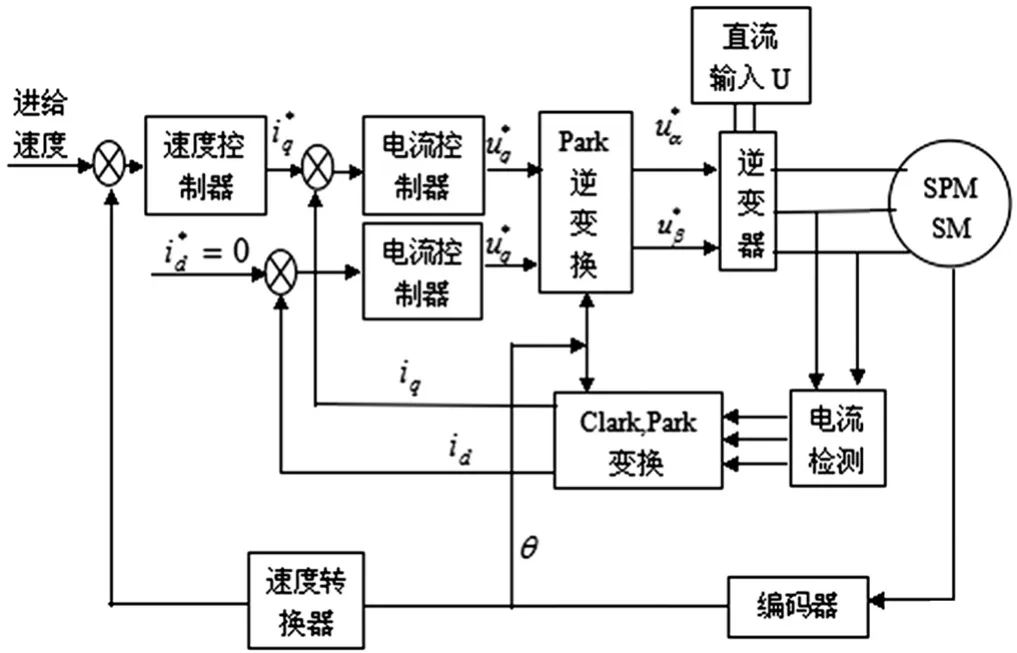
图1 永磁同步电机矢量控制系统框图
该伺服电机控制系统的控制过程可表示为:由图1所示的过程框图看出,进给速度给定信号与编码器检测到的转子转速信号相比较,经速度调节器的调节后,输出转矩电流分量指令信号,而d轴的参考输入电流为0,同时利用电流检测器采集永磁电机的定子三相交变电流,然后经CLARKE变换和PARK变换得q轴与d轴电流iq和 id,然后使、iq和、id相比较,并经过电流调节器的处理,得出d-q坐标系下的直轴电压u和交轴电压u。再通过Park逆变换电路可得α-β坐标系下的矢量电压u和u,由该矢量电压通过SVPWM模块产生六路PWM驱动控制信号,驱动逆变器中的开关器件。由此产生频率、幅值持续可变的三相正弦电流输入到永磁同步电机定子电枢,从而实现完整的速度电流双闭环的永磁同步电机矢量控制[7]。
2.2 SVPWM产生原理
三相桥式电压型逆变器是工业上最常用的逆变器拓扑结构,如图4是一个典型的电压型PWM逆变电路。该逆变电路通过控制6个开关管的开关状态和顺序的组合以及开关时间的调整来输出电机所需要的电流[8]。以得到谐波含量少、直流电源电压利用率高的输出。
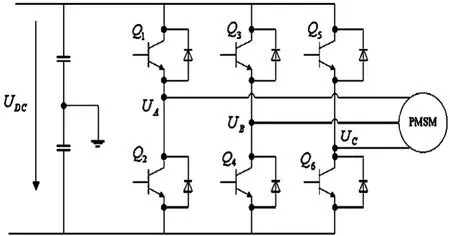
图2 三相桥式电压型逆变电路
如图2所示中的Q1~Q6是6个功率开关管,用a、b、c分别代表了3个桥臂的开关状态。规定:当上桥臂开关管处于“开”状态时(此时相应下桥臂开关管必然是“关”状态),其开关状态为“1”;当下桥臂开关管为“开”状态时(此时相应上桥臂开关管必然是“关”状态),则开关状态为“0”。这3个桥臂只有“1”或“0”两种状态,因此 a、b、c可形成 000、001、010、011、100、101、110、111共8种开关状态。其中000和111开关状态使逆变电路输出电压为零,所以称这两种开关状态为零状态[9],其八种状态如表1所示。

表1 矢量控制的开关导通8种状态与相电压和线电压的对应关系
3 软件模块及控制代码实现
在伺服电机控制领域,各个DSP厂家都有相对应的系列产品,例如TI公司的28x系列,Fre⁃escale公司的56F80x系列等,综合考虑控制方法所用时间和计算能力,位宽,浮点和定点等指标满足要求的情况下,选择TI公司的C2000系列中的28335作为控制器并利用电机控制模块实现电机仿真,其仿真电路见图3所示。
永磁同步伺服电机的控制程序是基于TI的DSP开发软件CCS平台编写,以下是PWM控制信号输出的一段程序:


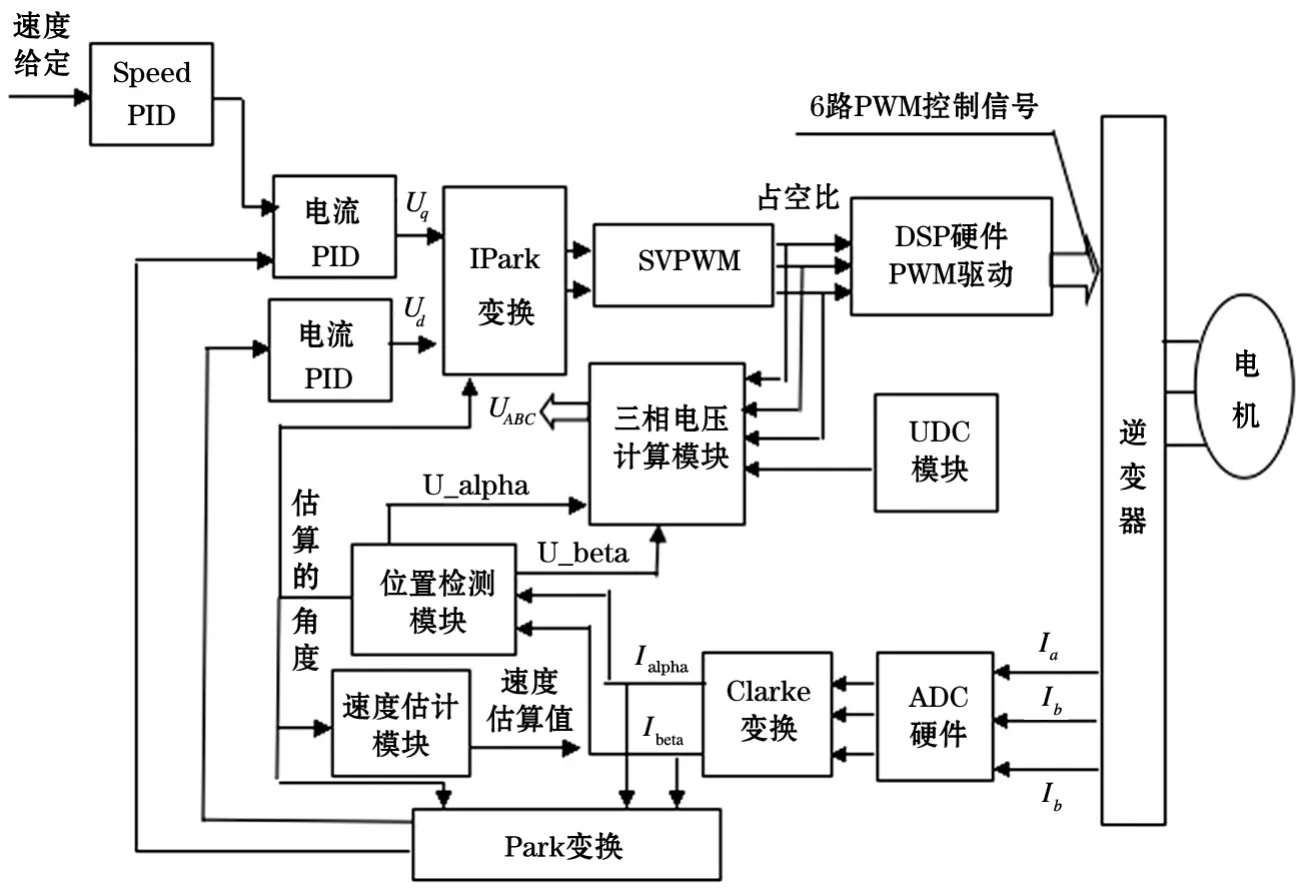
图3 伺服电机软件控制模块图

OC1C输出75%占空比
通过以上程序,实现了3种占空比类型的PWM控制信号的输出,在实际的程序应用中,取得了比较好的控制效果。
4 试验验证
根据上述永磁同步伺服电机的数学模型,采用DSP控制器完成电机三相电流的控制,并实现对电机电流,速度等的检测。该项目采用的CCS(Code Composer Studio)是TI公司提供的DSP软件开发环境,包含一整套用于开发和调试的工具。其中编译器、源码编辑器可实现源代码的编写和调试。而调试器、描述器、仿真器等均可实现数据可视化,该项目中对电机的启停,加减速控制进行了实验,数据图形描述如下。
如图4、5所示是电机在启动时的转速、转角和三相绕组电流的曲线,从图4中可以看出电机从零速到500 r/min的启动时间约为1 s,转速上升非常平滑,无过冲,并且预设转速与实际测量转速基本一致。转子转角的三种曲线的变化趋势相同,转角增加平稳、运行稳定,启动性能良好。从图5看出电机在启动过程中三相电流是正弦波形,谐波分量少,从而减少了谐波损耗,提高电机效率。

图4 电机启动转速转角图
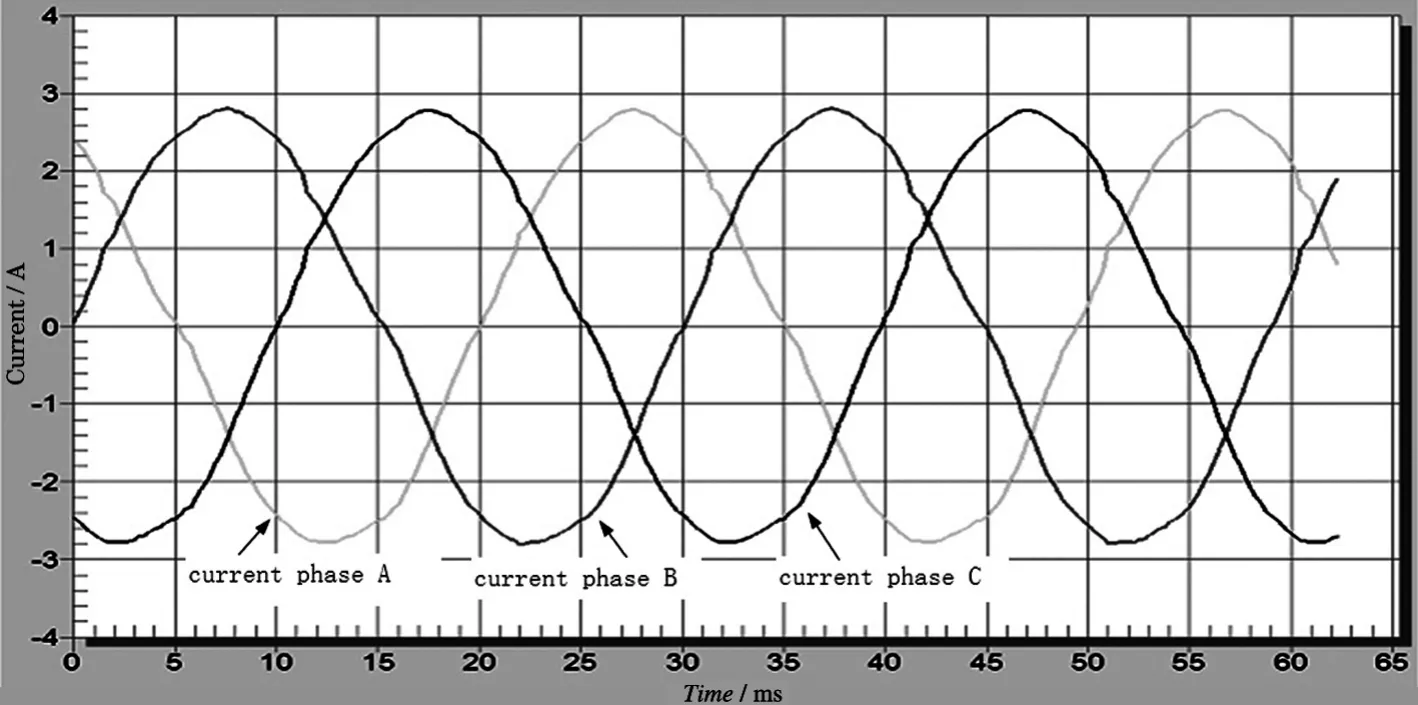
图5 启动时三相绕组电流波形图
如图6、7是DSP控制下伺服电机在阶跃响应的转速与电流曲线,由图6可见,实际转速与给定转速相比有一段时间滞后和平滑上升阶段,但响应转速平稳,且转速稳定时的波动小,下部分曲线表示了电机的控制电流的变化,此时在转速增加的时电流较大,稳定电流较小且稳定。图7是DSP控制下伺服电机在阶跃响应下的电流曲线电流响应曲线,可见电流给定曲线与响应曲线非常接近,响应时间短、无超调、电流响应平稳,所以该DSP控制具有优良的电流控制特性。
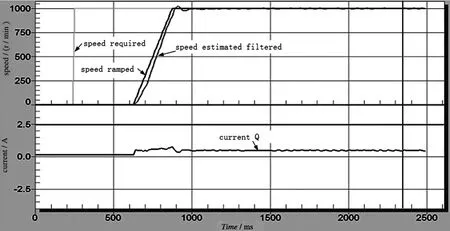
图6 基于阶跃信号的速度控制
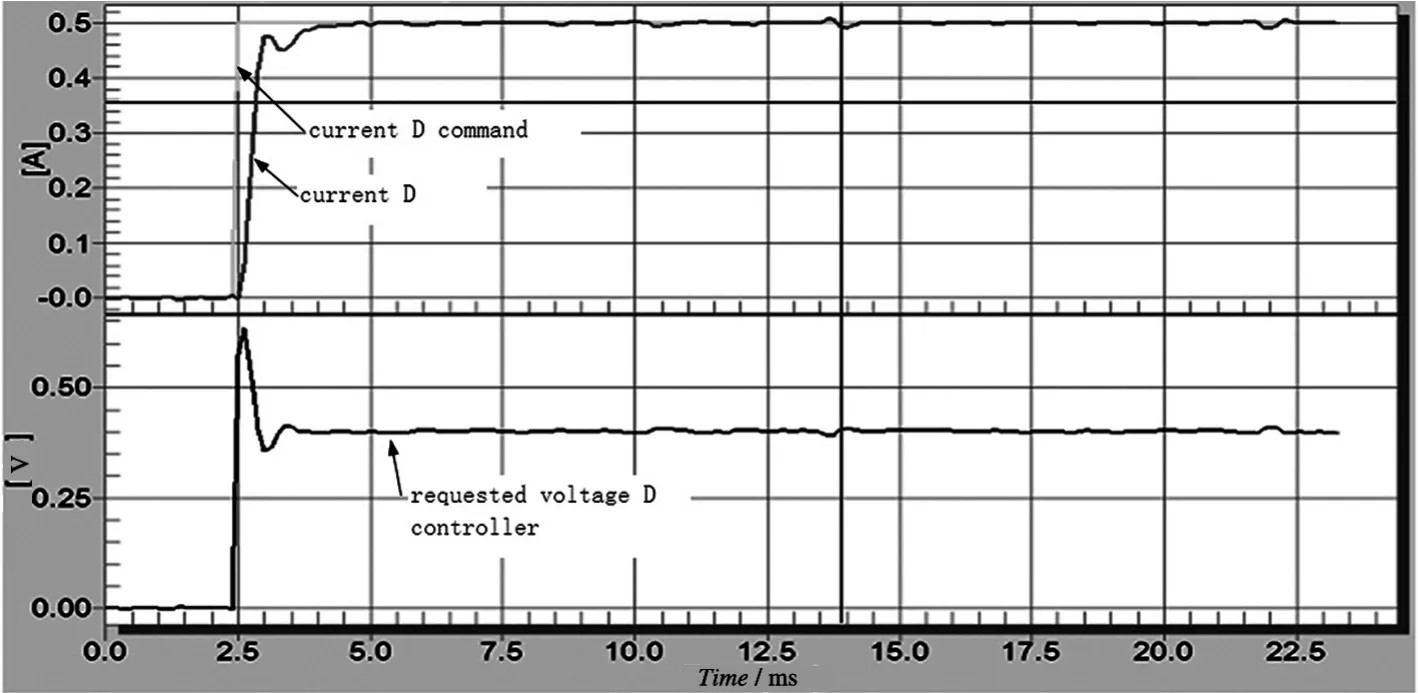
图7 阶跃响应下的电流曲线
5 结论
本文通过永磁同步伺服电机的应用场合,指出该类电机应具有的性能特性。为此对其数学模型进行了探讨和计算研究,并在此数学模型的基础上,应用DSP控制技术对永磁同步电机矢量控制系统进行了研究,通过电机运动控制的仿真与实验结果的对比,验证了算法的可行性和准确性,为今后电机应用和控制提供了理论指导和参考数据。
[1]谈勇.高速高精度雕铣机数控系统的研制[D].合肥:合肥工业大学,2004.
[2]叶益明.雕铣机数控系统应用集成研究[D].武汉:华中科技大学,2012.
[3]敖杰.基于TMS320LF2406A的永磁同步电机矢量控制系统研究[D].广州:华南理工大学,2012.
[4]高梅,王忠庆.基于DSP的交流伺服电机控制系统的研究[J].机械工程与自动化,2009(5):149-150.
[5]孟令东,曾志新.基于DSP交流伺服电机控制的制动系统的设计[J].DSP开发与应用,2006(5):153-155.
[6]冯国楠.现代伺服系统的分析与设计[M].北京:北京工业大学出版社,2001.
[7] Marwa Ezzat, Jesus de Leon, Nicolas Gonza⁃lez, Alain Glumineau. Sensorless Speed Control of Permanent Magnet Syn⁃chronous Motor by using Sliding Mode Observer[C].2010 11th Interna⁃tional Workshop on Vari⁃able Structure Systems. Mexico City, Mexico,June 26-28, 2010:227-232.
[8]Rusong Wu, Gordon R. Slemon.A Permanent Ma⁃gent Motor Drive Without a Shaft Sensor [J]. IEEE TRANSACTIONS ON INDUSTRY APPLI⁃CATIONS, 1991, 27(5):1005-1011.
[9]叶军军.基于MATLAB的永磁同步电机矢量控制系统仿真[J].商品储运与养护,2008,30(6):110-111.
[10]刘伯育.交流电机位置伺服系统的扰动补偿控制[J].机电工程,2014(1):97-100.
The PMSM Vector Control of Engraving and Milling Feeding System
WANG Xiao-dong1,WANG Tian-lei2
(1.Guangdong Kejie Machinery Automation Co.,Ltd.,Jiangmen529030,China;2.College of Information Engineering,Wuyi University,Jiangmen529020,China)
As a key component of feed system of CNC engraving and milling machine, the performance of control method of the permanent magnet synchronous AC servo motor(PMSM)plays an important role in the servo system.The mathematical model of PMSM is established and the vector control principle is described in detail.The current and speed double closed loop control of the servo motor is realized by using the DSP controller.The motor speed,current and angle are tested in control system are tested.Finally,verify the feasibility and accuracy of this control method by contrasting the results of motion control simulation with results of experiment,and providing theoretical basis for the control of the motor and the application in the NC machine tool.
permanent magnet synchronous motor;vector control;CCS
TM341
:A
:1009-9492(2014)12-0042-05
10.3969/j.issn.1009-9492.2014.12.010
王小东,男,1981年生,内蒙古赤峰人,硕士,工程师。研究领域:数控系统研究与开发。已发表论文5篇。
(编辑:阮 毅)
*广东省重大科技专项(编号:2010A080401003)
2014-09-11
