一类一阶变系数线性微分方程组解的结构

符云锦

一类一阶变系数线性微分方程组解的结构

符云锦

（凤凰县两林学区，湖南凤凰 416211）

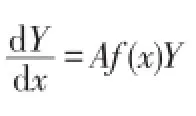
变系数；微分方程组；解法；通解

解一阶变系数线性非齐次微分方程组

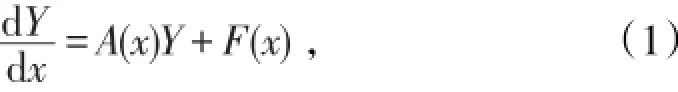
关键是能否求出其对应的齐次微分方程组

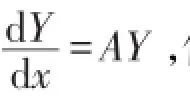
的通解。本文基于文献〔10〕的条件上，给出了一类变系数线性微分方程组的求解方法。为了说明的方便，先给出一个定义。

定义设矩阵A、B为n阶方阵，若AB=BA，则称矩阵A与B可以交换。下面给出2个引理。

1 引理

引理1 设n阶方阵A、B可以交换，则

其中 f(χ)为可积函数。

证明:由条件 BA=AB，易得 BA2=A2B，BA3=A3B，BA4=A4B…

根据指数矩阵的定义，可有

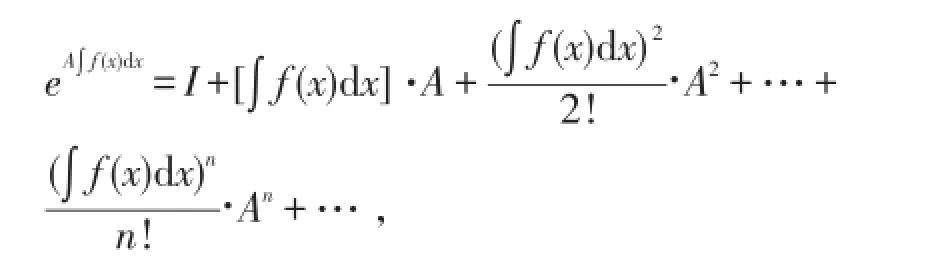
则有

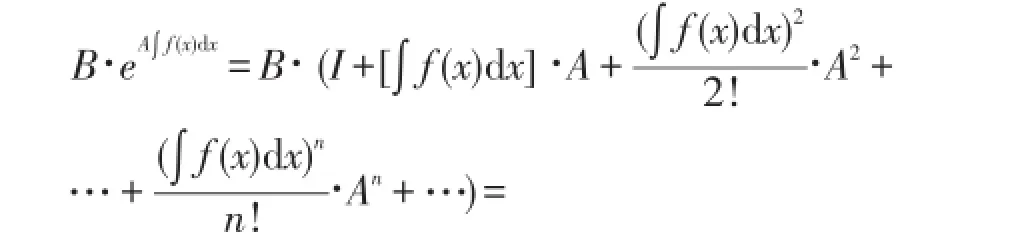
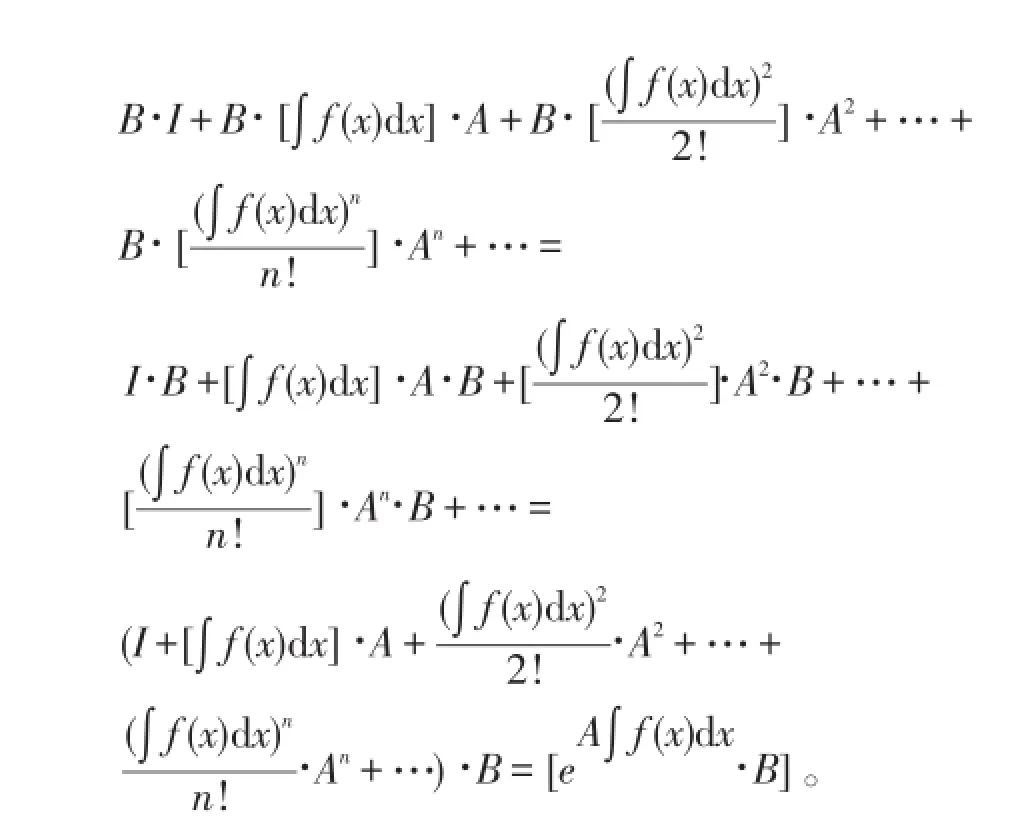
引理2 设n阶方阵C分别与n阶方阵A、B可以交换，则

其中f(χ)、g(χ)为可积函数。

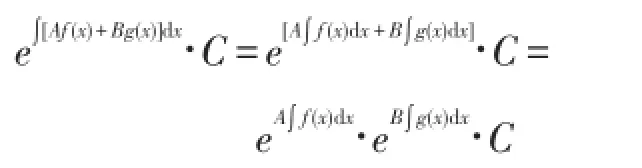
由引理1，可得

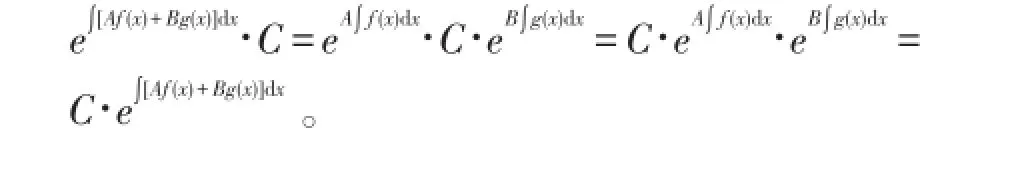
2 主要结果

定理1 设Y1、Y2分别是一阶线性齐次微分方程组

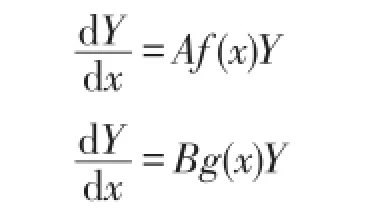
的通解，且满足BA=AB，则一阶线性齐次微分方程组

的通解为

其中 f(χ)、g(χ)为可积函数。

证明:

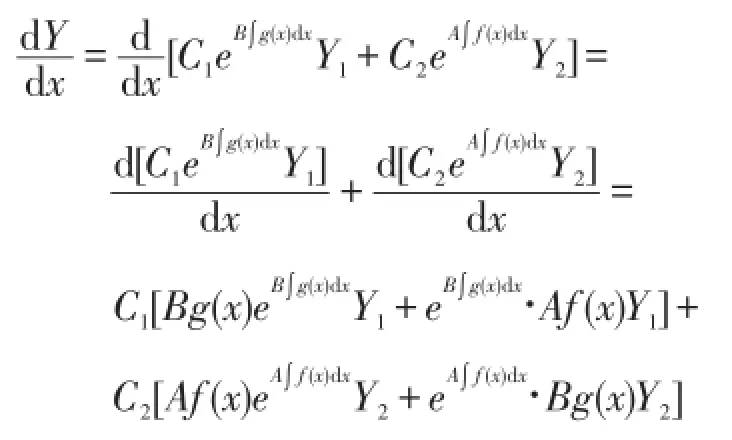
由引理1，易得

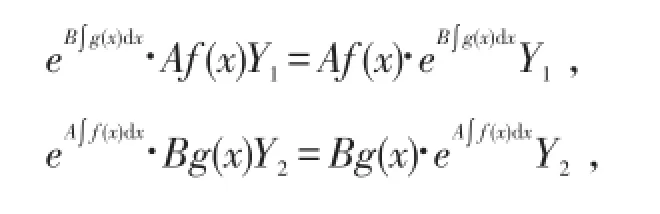
所以

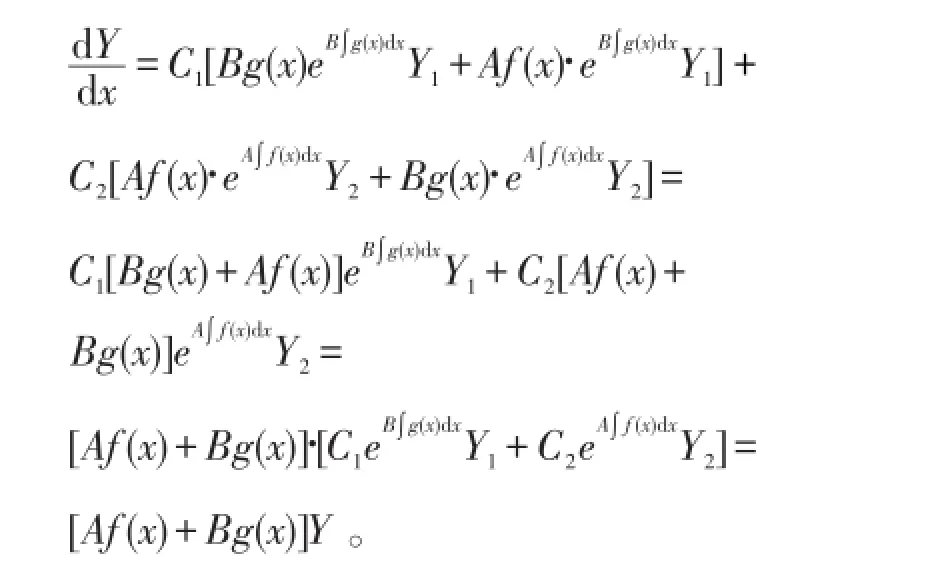
定理2 设n阶方阵Y1，Y2，…，Yn分别是一阶线性齐次微分方程组

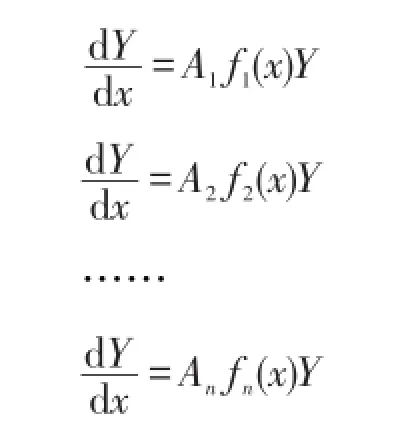
的通解，且满足A1，A2，…，An可以两两交换，则一阶线性齐次微分方程组

离子液体是由离子组成的有机盐化合物，在室温下多为流动状态的液体，对纤维素等聚合物具有良好的溶解性能。在纤维素向5-HMF的催化转化过程中，离子液体被广泛采用[12]。

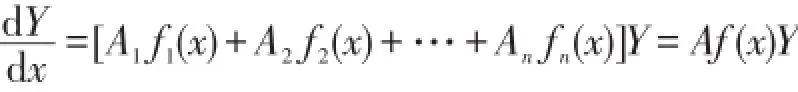
的通解为

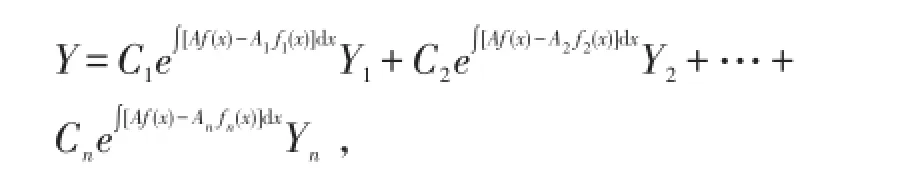
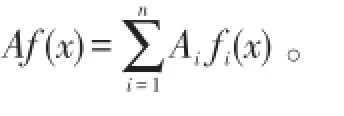
证明：

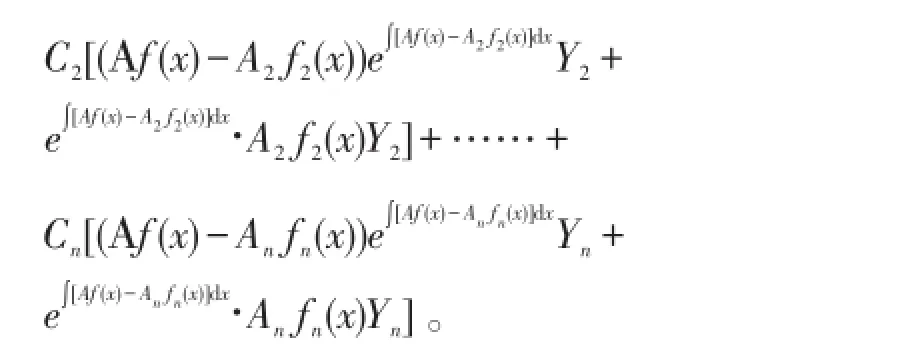
由引理2，易得

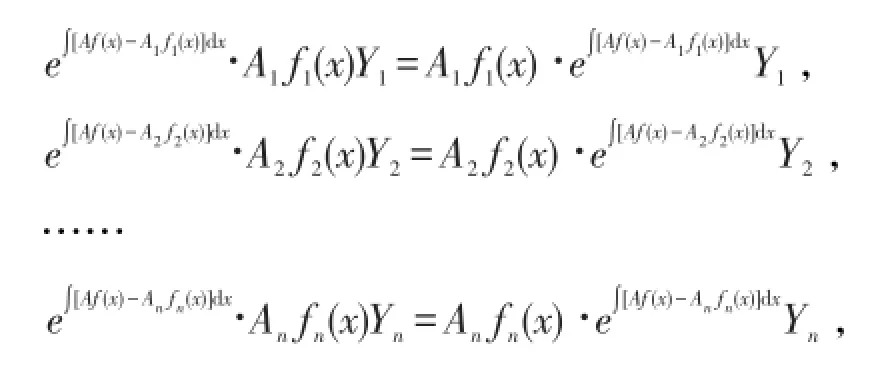
所以

根据定理1和定理2，容易得出下面2个推论。

推论1 设Y1、Y2分别是一阶变系数线性齐次微分方程组

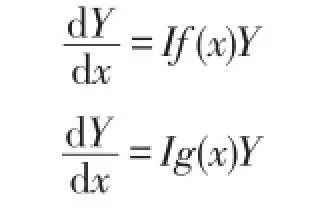
的通解，则一阶变系数线性齐次微分方程组

的通解为

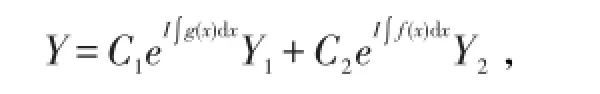
其中f(χ)、g(χ)为可积函数。

推论2 设n阶方阵Y1，Y2，…，Yn分别是一阶变系数线性齐次微分方程组

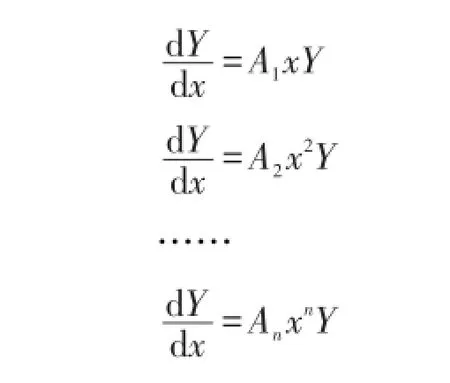
的通解，且满足A1，A2，…，An可以两两交换，则一阶变系数线性齐次微分方程组

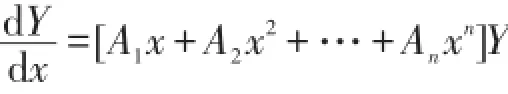
的通解为

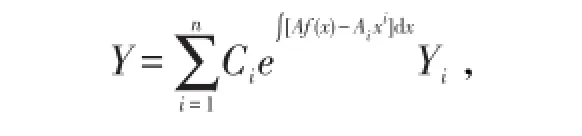
〔1〕化存才，赵奎奇，杨慧，等.常微分方程解法与建模应用选讲〔M〕.北京：科学出版社，2009：86-116.

〔2〕钱祥征，黄立宏.常微分方程〔M〕.长沙：湖南大学出版社，2008：73-80.

〔3〕阿布力米提·米吉提.几类变系数线性微分方程组的可解型〔J〕.伊犁师范学院学报，2006（3）：30-33.

〔4〕阿布力米提·米吉提.变系数齐线性微分方程组的又一类可解型〔J〕.伊犁师范学院学报，2000（4）：81-83.

〔5〕曹玉平.一阶线性变系数微分方程组的矩阵解法〔J〕.河北理工学院学报，2005，27（2）：111-114.

〔6〕韩京苑.函数矩阵eA（t）与变系数线性微分方程组初值解的表达式〔J〕.山东师范大学学报：自然科学版，2007，22（2）：20-22.

〔7〕李长江，陈军，郝慧伟.一类一阶变系数线性微分方程组的通积分〔J〕.科技通报，2010，26（4）：486-488.

〔8〕李建湘.变系数线性齐次常微分方程组的λ-矩阵求解法〔J〕.数学的实践与认识，2002，32（3）：470-475.

〔9〕阳凌云，符云锦.一阶线性微分方程组的解法新探〔J〕.湖南工业大学学报，2010，24（1）：16-19.

（责任编辑 袁 霞）

The Structure on Solution of a Kind of First-order Variable Coefficient Linear Differential System of Equations

FU Yunjin
（Lianglin School District of Fenghuang，Fenghuang,Hunan 416211，China）

Based on the general solution of the first order variable coefficient linear homogeneous differential equations of（f(χ)is an integral function），the solutions of first order variable coefficient linear differential equations are further explored，and the structure theorem of the general solution is provided.

variable coefficients；differential equation systems；solving method；general solution

O175.1

A

1672-2345（2014）06-0004-03

10.3969∕j.issn.1672-2345.2014.06.002

2013-09-16

符云锦，主要从事初等数学、微分方程、分析学和教育理论及其应用研究.