一类二阶Hamilton系统周期解的存在性

王少敏

（大理学院数学与计算机学院，云南大理 671003）

一类二阶Hamilton系统周期解的存在性

王少敏

（大理学院数学与计算机学院，云南大理 671003）

利用临界点理论研究以下二阶系统

周期解；极小作用原理；二阶系统

1 引言和主要结果

考虑二阶系统

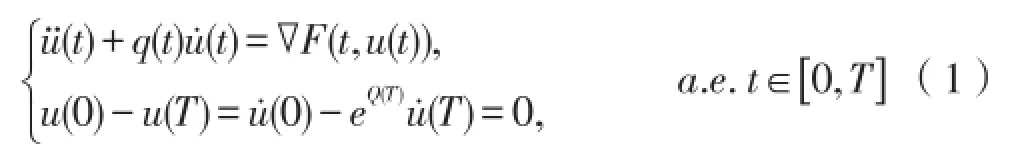
(A)F(t,χ)对于每个 χ∈RN关于t可测，对于关于χ是连续可微的，存在a∈C(R+,R+), b∈L1(0,T;R+)使得

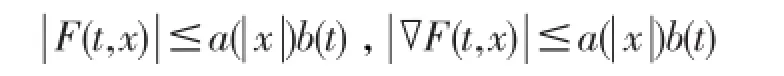
对于χ∈RN和a.e.t∈[0 ,T]成立。

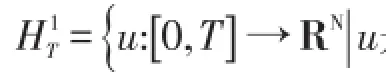
其等价于如下范数

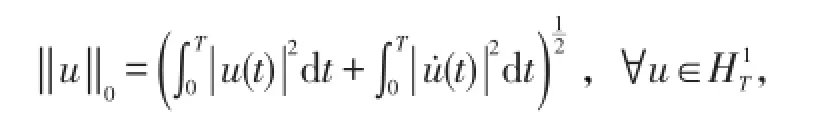
相应泛函

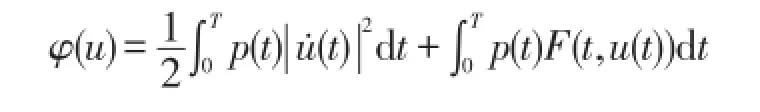
定理A 设F(t,χ)=F1(t,χ)+F2(χ)满足假设(A)及以下条件〔4〕：

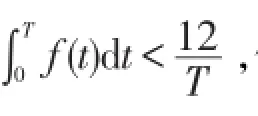
(ii)存在常数α∈[0,2)和r>0，使得对一切χ，y∈RN有

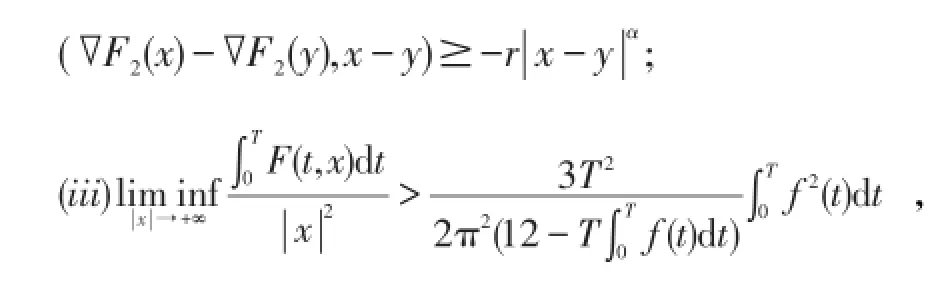
由于受到这个定理的启发，本文获得了系统（1）的如下存在性定理。

定理1 设F(t,χ)=F1(t,χ)+F2(χ)满足假设(A)以及F1(t,χ)，F2(χ)满足以下条件：

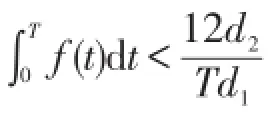
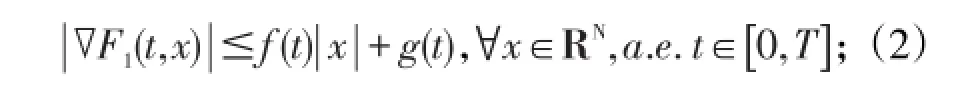
(ii)存在常数α∈[0,2)和r>0，使得对一切χ，y∈RN，有则问题（1）在上至少存在一个极小化φ的周期解。

2 定理的证明

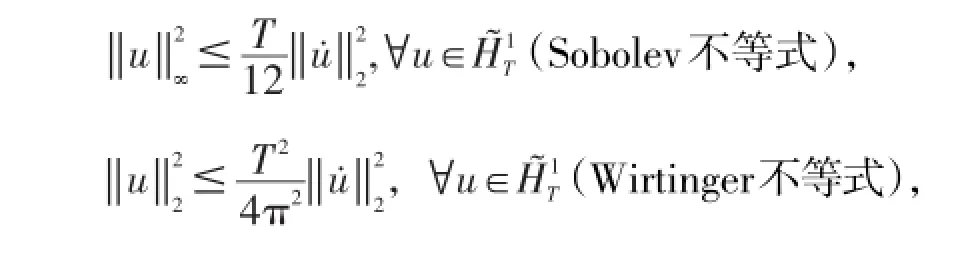
证明：由定理1中条件（iii）可选择

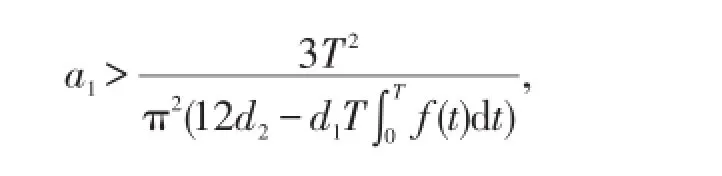
存在M，使得

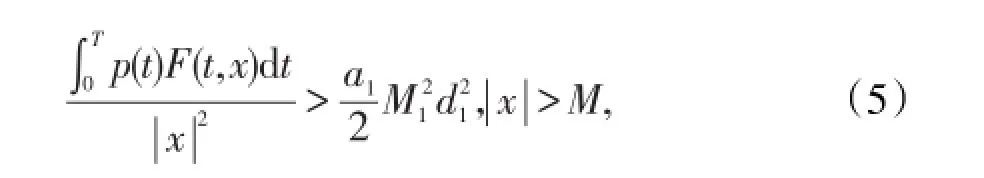
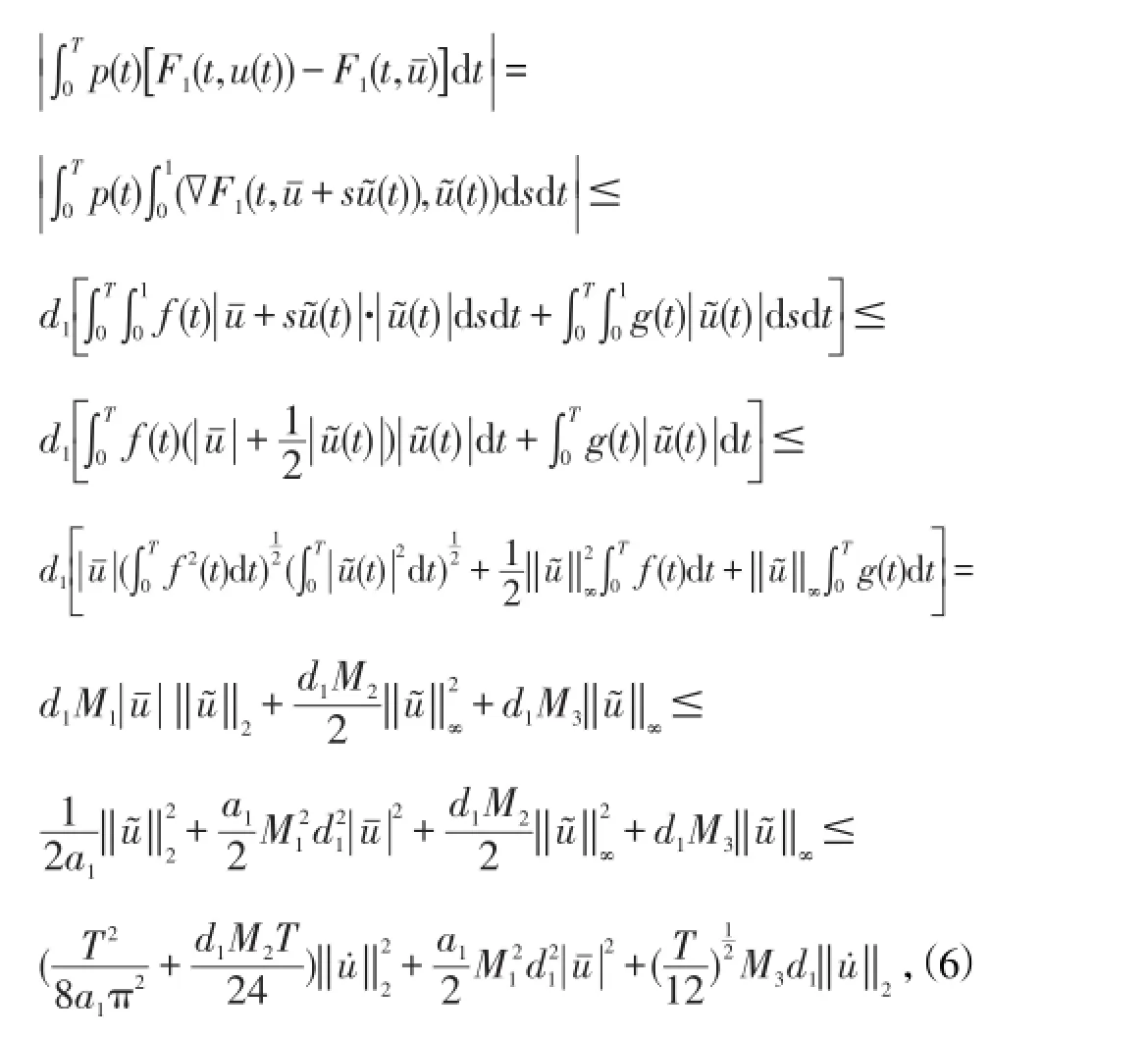
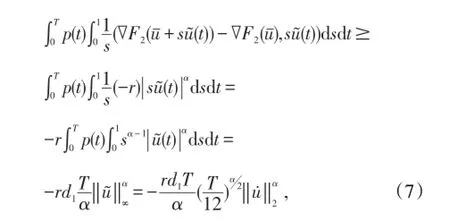
由（6）式，（7）式，有

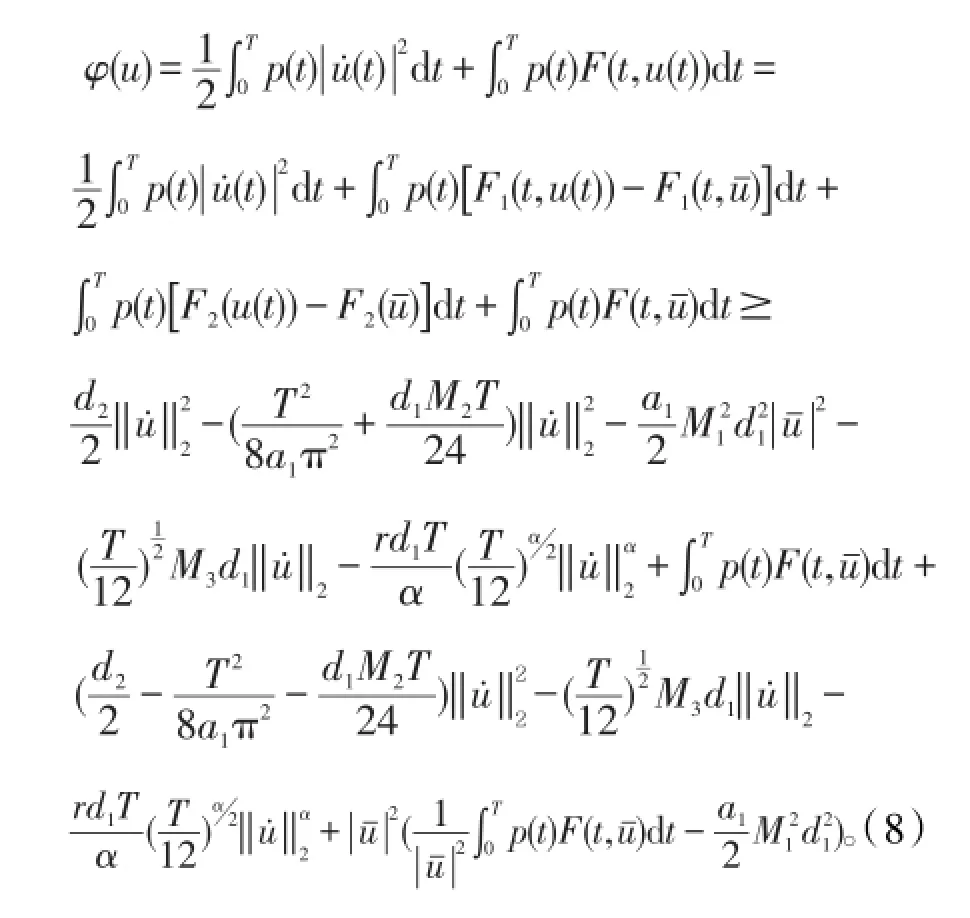
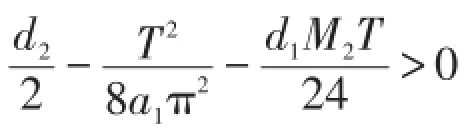
注：本文定理1的条件新颖，因此所得的结果具有一定的创新性。

〔1〕WU X，CHEN S X，TENG K M.On variational methods for a class of damped vibration problems〔J〕.Nonlinear Anal.，2008，68（6）:1432-1441.

〔2〕RABINOWITZ P H.On subharmonic solutions of Hamilto⁃nian systems〔J〕.Comm.Pure Appl.Math.，1980（33）:609-633.

〔3〕MAWHIN J，WILLEM M.Critical Point Theory and Hamil⁃tonian Systems〔M〕.Berlin∕New York:Springer-Verlag，1989.

〔4〕吴越，安天庆.一类非自治二阶哈密顿系统的周期解〔J〕.吉林大学学报：理学版，2013，51（1）：57-63.

〔5〕TANG C L，WU X P.Periodic solutions for a class of nonautonomous subquadratic second order Hamiltonian sys⁃tems〔J〕.J.Math.Anal.Appl.，2002，275（2）:870-882.

〔6〕TANG C L.Periodic solutions for non-autonomous second order systems with sublinear nonlinearity〔J〕.Proc.Amer. Math.Soc.，1998，126（11）:3263-3270.

〔7〕TANG C L，WU X P.Periodic solutions for second order systems with not uniformly coercive potential〔J〕.J.Math. Anal.Appl.，2001，259（2）:386-397.

〔8〕TANG C L，WU X P.Periodic solutions of a class of nonautonomous second order systems〔J〕.J.Math.Anal.Ap⁃pl.，1999，236（2）:227-235.

〔9〕王少敏，熊明，茶国智.一类非自治二阶系统的周期解〔J〕.大理学院学报，2012，11（4）：11-13.

〔10〕裴瑞昌，李海合.一类二阶Hamiltonian系统的无穷多周期解〔J〕.纯粹数学与应用数学学报，2009，25（4）: 690-694.

（责任编辑 袁 霞）

Existence of Periodic Solutions for a Class of Second Hamilton Systems

WANG Shaomin
（College of Mathematics and Computer,Dali University,Dali,Yunnan 671003，China）

periodic solutions;the least action principle；second order systems

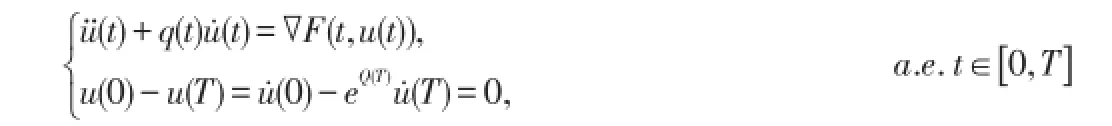
O177.25

A

1672-2345（2014）06-0001-03

10.3969∕j.issn.1672-2345.2014.06.001

云南省科技厅应用基础基金资助项目（2011FZ167）

2013-09-25

2013-10-27

王少敏，副教授，主要从事非线性分析研究.

的周期解的存在性。在非线性项F(t,χ)=F1(t,χ)+F2(χ)满足假设（A）及F1(t,χ),F2(χ)分别满足一定有界性条件下，通过使用极小作用原理获得了一个新的存在性定理。