拖缆涡激振动特性分析

张 莺，张作琼

（中国船舶重工集团公司第七一〇研究所，湖北宜昌 443003）

拖缆涡激振动特性分析

张 莺，张作琼

（中国船舶重工集团公司第七一〇研究所，湖北宜昌 443003）

建立了拖缆振动模型，对拖缆流场进行了仿真分析，预报了拖曳过程中拖缆的振动情况，通过对不同工况下的涡激振动特性进行对比，得出拖缆涡激振动的规律。

涡激振动；水动力系数；仿真；拖缆

0 引言

流体流经钝体时，结构尾迹中的漩涡以一定的频率交替脱落，产生周期震荡的升力，结构在升力的作用下以一定的频率和振幅振动，这种现象称为涡激振动，水下拖缆一般为钝体，水下运动时，流体作用力导致产生振动，引起拖曳阻力增加。

拖缆振动的危害很大，尤其在高速拖曳过程中，拖缆的振动加剧，使阻力大幅增加，影响水下拖曳系统的拖曳姿态，不利于水下拖曳系统的研制。本文建立拖缆振动模型，对拖缆流场进行仿真分析，对拖曳过程中拖缆振动情况进行预报，对不同工况下的涡激振动特性进行对比，得出拖缆振动的规律。

1 研究模型

1.1 立柱振动模型

研究最广泛的模型是尾流振荡器模型，把临近尾流当作一个耦合于工程结构的非线性自激振荡器来处理[1]。

单自由度系统可以简化为弹簧-阻尼-质量系统，只考虑圆柱的横向振动；最新也有研究两自由度系统，同时考虑横向振动和流向振动。

圆柱在横向的运动方程可表示为：

以后研究的各种模型都是在基本的尾流振动器模型上加以补充和局部改变的。宋芳[2]建立了一个新的结构-尾流振子耦合模型，流场近尾迹动力学特征被膜化为非线性阻尼振子，采用vander Pol方程描述，以控制体中结构与近尾迹流体间受力互为反作用关系来实现流固耦合。XU Wan-hai[3]研究了一种新型的尾流振子模型，在这种新型模型中，就经验参数和质量比对振动响应的控制做了些改进的假设，通过实验验证，取得了较好的效果。

1.2 拖缆振动模型

拖缆相比于立柱，细长度更大，且缆张力沿缆长方向变化，其分析不同于立柱，一般在分析拖缆振动时，可简化为两种模型：一是弦模型，它忽略了拖缆弯曲刚度的影响；另一种是梁模型，考虑了缆绳弯曲刚度的影响。

考虑横向振动的水下拖曳缆绳为梁，其弯曲硬度为EI，非均匀张力为T(z)，单位长度的有效质量为m(t)，在横向力为Fy(z ,t)的作用下横向振动模型为：

忽略缆的非均匀张力T(z)的影响求固有频率，方程为：

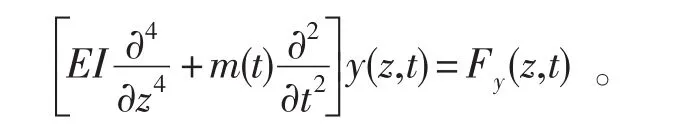
2 重要的结构参数的影响

2.1 斯特罗哈数St

在固定圆柱的绕流问题中，通过斯特罗哈数及将边界层分离以及流动的不稳定性这些内在的物理特性与相对稳定的涡的脱落频率 fSt联系在一起。斯特罗哈数的定义为：

斯特罗哈数St同雷诺数Re的关系。从图1中可以看到，在亚临界雷诺数区域St数比较稳定，大概在0.2左右，意味着涡的脱落比较有序。在临界区域St数的数值比较紊乱，涡的脱落频率分布在一个频率带宽范围内。

图1 斯特罗哈数St与雷诺数Re的关系

2.2 刚度

随着刚度的变化，圆柱涡激振动特性具有明显的分支，且各支的特性具有明显的差异，在不同分支中观察到不同的旋涡脱落模态。旋涡脱落模态的形式与涡激振动的响应、涡激力系数的特性密切相关[4]。

2.3 约化速度、无量纲振幅和频率比

频率比=fnfs（fn是结构的固有频率， fs是圆柱在固定状态下的漩涡脱落频率），随着频率比的增大，最大位移、升力系数、阻力系数变化趋势相似，达到各自巅峰后逐渐降低，最后接近固定绕流的结果；涡激共振点发生偏移，质量比越小则偏离越大[5]。

在涡激情况下，弹性柱体的振动现象不能用一般的强迫振动理论去解释。一旦涡泄频率 fs接近圆柱的固有频率 fn，则圆柱将在一个速度范围内保持以接近固有频率的频率振动，其原因是尾流和圆柱运动之间的相互影响，即结构的振动反过来对流场产生影响，产生频率锁定（Lock in），即涡泄频率和固有频率同步（Synchronization），当涡泄频率接近固有频率的整数倍时，也会产生频率锁定。锁定的频率宽度（即锁定范围）约为fs的±25%～30%，且随着振幅的增大而增大。对于水中的情况，锁定范围约为4.5＜Vr＜10.0，最大振幅在6.5＜Vr＜8.0。

2.4 质量比和结构阻尼

模型质量对模型所排出的流体质量之比为质量比。质量比对涡激振动横流向位移的影响完全是非线性的。然而结构阻尼比的影响则几乎是线性的。

2.5 雷诺数

在质量阻尼一定的情况下，涡激振动的响应强度随着雷诺数的增加而下降。

3 计算方法

3.1 计算区域

计算区域如图2所示，为一长45D，宽30D的长方形。进流边界距离圆柱中心15D，出流边界距离圆柱中心30D。

图2 计算区域示意图

3.2 边界条件

本文包括下列边界（D为圆柱直径）：

（1）速度入口（velocity inlet）：距离圆柱中心15D，设定来流速度的大小与方向，n=；

（2）压力出口（pressure outlet）：距离圆柱中心30D，认为流动在该处已经充分发展，故边界条件使用压力出口；

（3）壁面（wall）：圆柱表面，设定无滑移条件，u=v=w=0；

（4）外场：因为流域外表面距离圆柱足够远，故可以认为在该面上没有法向速度，因此可以取边界条件为速度入口（velocity inlet）。

3.3 网格划分

采用全结构网格，通过不同的网格式进行计算，验证网格的独立性。计算网格总数为34 300。

图3和图4为计算域的网格和圆柱周围的局部网格。

图3 计算域网格

本文的计算采用SIMPLEC算法结合RNG k-ε湍流模型来计算求解雷诺平均纳维-斯托克斯方程（RANS）。对于压力方程采用标准的离散格式进行离散，对于动量方程、湍流方程、雷诺应力方程，均采用二阶迎风格式进行离散。其中湍流强度的设置根据经验公式得来：

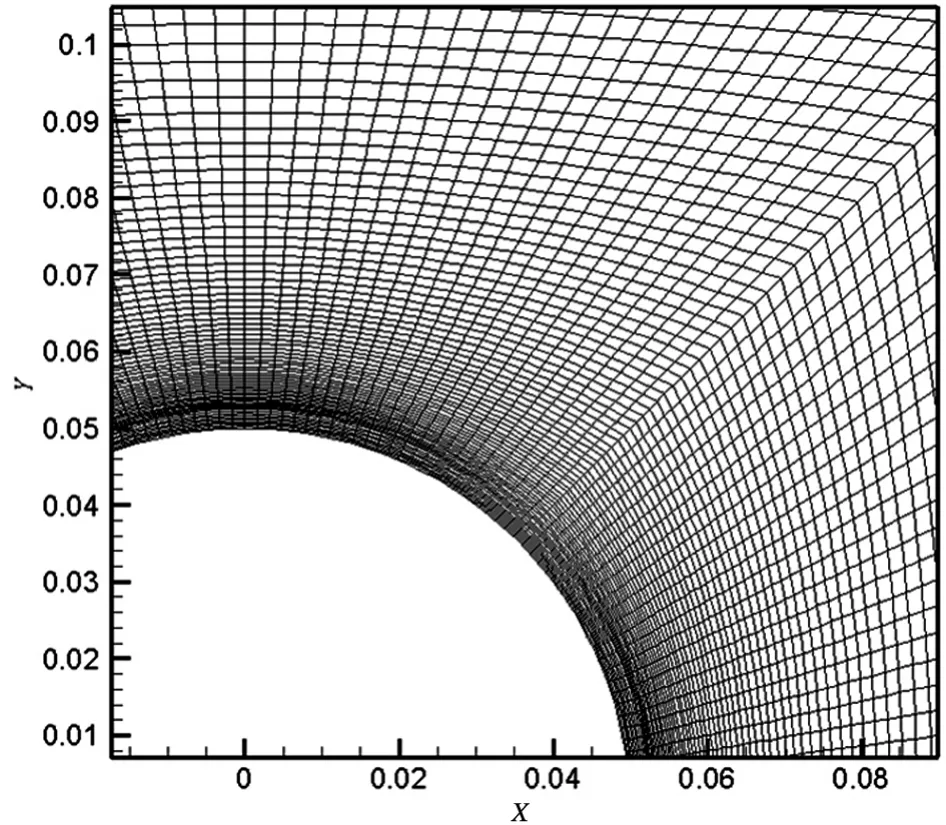
图4 圆周周围局部网格

3.4 水动力系数定义

阻力系数：

升力系数：

斯特罗哈数：St=fsD/v。

其中：D为阻力；L为升力；l为特征长度，计算时取为圆柱的直径； fs为涡泄频率。

4 计算结果与分析

图5为不同直径、不同航速圆柱表面的平均压强。由图5可知，在一定航速下，随着圆柱直径的增加，圆柱表面的平均压强逐渐增大，但是增大的较缓慢。一定直径下，随着航速的增加，圆柱表面的平均压强逐渐增大，增长的幅度不明显。

图6为不同直径、不同航速圆柱的阻力系数。

图7为不同直径、不同航速圆柱的涡脱落周期T。

图5 不同直径、不同速度圆柱表面压力

图6 不同直径、不同速度圆柱的阻力系数

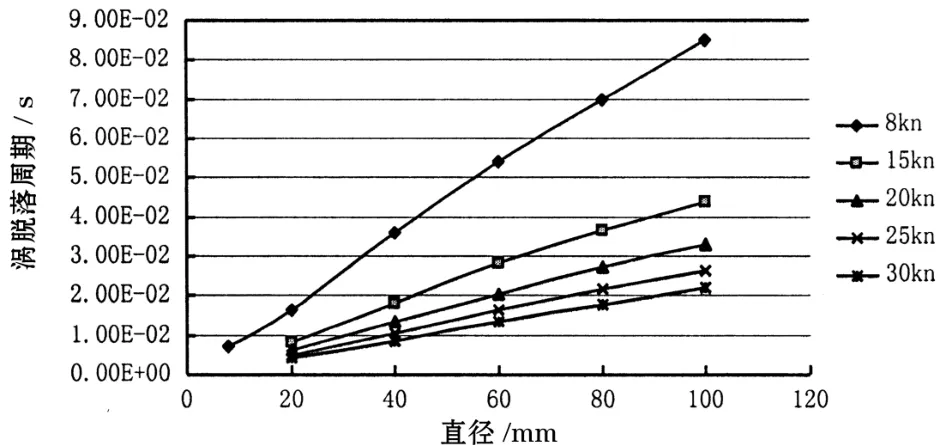
图7 不同直径、不同速度圆柱的涡脱落周期

图8为不同直径、不同航速圆柱的涡泄频率f（Hz）。由图可以看出，在直径一定的情况下，航速越大，涡泄频率越小；航速一定的情况下，直径越大，涡泄频率越小。这说明涡泄频率与雷诺数呈反比关系。

图8 不同直径、不同速度圆柱的涡泄频率

图9为不同直径、不同航速圆柱的斯特罗哈数St。在文中所计算的雷诺数范围内，斯特罗哈数呈现出不确定性，这与湍流的随机性关系密切。但在这一段雷诺数范围内，斯特罗哈数基本在0.3左右变化。

图9 不同直径、不同速度圆柱的斯特罗哈数

5 结束语

拖缆振动研究一直是水下拖曳系统研究关注的焦点，在高航速拖曳情况下，拖缆振动剧烈，对水下拖体姿态影响较大。本文通过对不同工况下拖缆的表面压力、阻力系数、涡脱落周期、涡泄频率、斯特罗哈数等涡激振动特性进行对比，分析拖缆振动机理，得出拖缆涡激振动的规律，为拖缆振动抑制技术的研究提供依据。

［1］潘志远.低质量—阻尼因子圆柱体的涡激振动预报模型［J］.船舶力学，2005，9（5）：115-125.

［2］宋芳.圆柱涡激振动的结构—尾流振子耦合模型研究［J］.力学学报，2010，42（4）：357-366.

［3］XU Wan-hai.A new wake oscillator model for predicting vortex induced vibration of a circular cylinder［J］.Jour⁃nal of Hydrodynamics，2010，22（3）：381-386.

［4］周国成.圆柱涡激振动数值模拟研究［J］.噪声与振动控制，2010，30（5）：51-57.

［5］徐枫，欧进萍.低雷诺数下的弹性圆柱体涡激振动及影响参数分析［J］.计算力学学报，2009，26（5）：613-619.

Analysis of Cable’s Vortex-Induced Vibration Characteristics

ZHANG Ying，ZHANG Zuo-qiong
（No.710 R&D Institute CSIC，Yichang443000，China）

Established the vibration model of cable，and forecasted the vibration of towed cable by simulating the flow field.By comparing the vortex-induced vibration characteristics under different working conditions，indicated the vortex-induced vibration disciplinarian of cable.

vortex-induced vibration；hydrodynamics coefficient；simulation；towed cable

TN911

A

1009－9492(2014)02－0069－04

10.3969/j.issn.1009-9492.2014.02.020

张 莺，1984年生，河南许昌人，硕士，工程师。研究领域：液体动力分析、机械设计及总体技术。已发表论文12篇。

(编辑：向飞)

2013－08－04