以不变应万变——浅谈解决函数最值(值域)问题的“天龙八式”

赵 杰

(江苏省海门市三厂中学，江苏海门，226121)

2013年江苏省数学高考试卷中的第9题、第14题、第20题，2012年江苏省数学高考试卷中第8题、第12题、第13题、第17题、第19题，2011年江苏省数学高考试卷中第8题、第12题、第13题、第14题、第17题都有所涉及函数的最值(值域)问题。它出现在试卷上的题型不一，有的以填空题形式出现，有的以解答题形式出现。它又和其他知识整合在一起，例如与方程、不等式及某些几何知识紧密联系在一起。这类题对于学生的分析能力要求特别高，综合性强，还要懂得变通，令学生非常头疼，所以函数的最值(值域)问题成了高中数学中的一个重点，也是一个难点。因此，笔者针对高中阶段遇见的最值(值域)问题，归纳出常用、有效的八种方法，并把它取名为“天龙八式”。

第一式：图像法

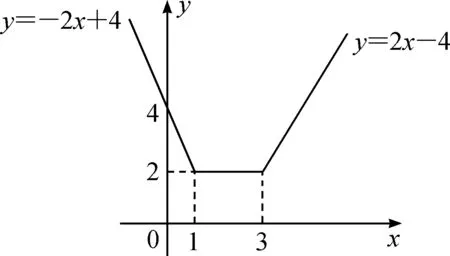
作为“天龙八式”的起始式，图像法具有简洁、明了、直观、易懂等特性，也是被许多学生所青睐的一种方法，但它只能解决一些简单函数，学生必须能准确的画出它的图像才能施之可行。

例如：求函数f(x)=|x-3|+|x-1|的值域。

第二式：分离常数法

分离常数是我们针对一次分式函数求最值常用的一种方法，但要引起高度重视的是一定要把分子上的变量全部化掉，要不然我们还是不能达到应要的目标。

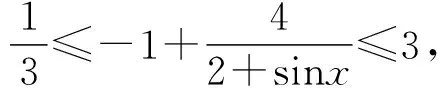
第三式：换元法

换元法是我们高中阶段最常用的方法之一，它最重要的功能是把一个复杂问题通过换元后变简单化。在这里，我们通过换元法能把一些复合函数简单化，一些陌生函数熟悉化，从而更容易地解决问题。

第四式：单调性法

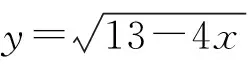
第五式：基本不等式法

基本不等式在高考考纲要求中是八个C级要求之一，可见它的重要性是不可忽视的。而在使用基本不等式的过程中除了要掌握它的使用条件“一正，二定，三相等”以外，我们的学生还要能看出如何使用基本不等式。

第六式：参数法

参数法是我们在选修4系列中学到的一种技巧，这也为理科的学生提供了一种解题的方法。这种方法的关键是把方程转换为参数方程，然后再去求最值。

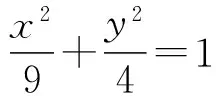
第七式：数形结合法

庞加莱说过：“感觉到数学的美，感觉到数与形的协调，感觉到几何的优雅，这是所有真正的数学家都清楚的真实的美的感觉。”数形结合作为高中数学四大思想之一，它的用途非常广泛，它把代数和几何做了一个完美的融合。所以要能很好地运用数形结合，学生必须要掌握好相关知识的几何意义。对函数而言，常用的几何意义有截距、斜率、距离和面积等。

终极式：导数法

作为“天龙八式”的终极式，导数法有着一招定乾坤的威力，凡是函数求最值问题，无论是简单函数还是复合函数，理论上我们都可以用导数法解决，只不过有些问题我们用前面的方法更方便。

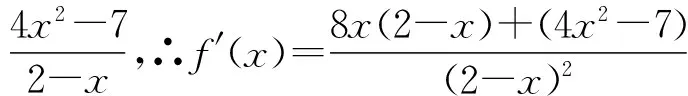
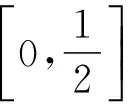
则f(x)的值域为[-4,-3]。

叶圣陶先生说过：“教师之为教，不在全盘授予，而在相机诱导。”当然，解决最值(值域)问题的方法远远不止这些，例如，还有判别式法，反函数法等。这里的“天龙八式”只是对常见的求最值问题作一个归纳，而且有时在同一个题目中，解决的方法也可以几种通用或者几种并用。总而言之，解决函数的最值(值域)问题，关键还是要掌握这几种方法，然后以不变应万变，具体问题具体分析，能灵活运用这几种方法解决问题。

[1] 席美能.最值问题之笔者见[J].中学生数理化：教与学，2011(8).

[2] 张琳琳.形如Y=f(x,y)的二元函数的最值的求法[J].科教新报：教育科研，2011(23).

[3] 江怀起.函数值域的求法分析类析[J].数学教学研究，2008(S2).