不同特性介质对边壁流效应的影响
2014-02-09苑艺琳王福刚高振凯
苑艺琳, 王福刚, 靖 晶, 高振凯
(吉林大学 环境与资源学院, 地下能源与废物处置研究所, 吉林 长春 130021)
0 引 言
边壁流效应是指一定的水力条件下,保持有某种物理属性和化学成分的流体,在某种介质中渗透时,受边壁粗糙度、几何特征以及水理性质的影响[1],而发生在边界附近的不均匀水流渗透和溶质运移过程[2-3]。在室内水流或溶质运移实验过程中,该效应一旦发生,对地下水渗流和溶质的时空分布将产生影响,干扰实验结果。
边壁流效应在多个领域受到科学工作者的注意,但孔隙介质地下水渗流和溶质(或污染质)运移实验中,边壁流效应还没有引起研究人员的足够重视,目前对边壁流效应的研究仍处于定性研究阶段,并且缺乏系统性和全面性。
本文以室内物理实验获取的第一手数据为基础,以现代计算机技术、实验数据多种数学分析方法为手段[4],结合并吸取现代水力学中边界层理论在实际应用研究中的经验和成果[5],从与边壁流效应有成生联系的实验介质特征(介质属性特征)角度出发,研究边壁流效应发展过程和影响因素。通过实验室试验,研究不同介质特征下,边壁流效应影响区域与渗流核心区的水流质量交换和流速差异所引起的渗流场、浓度场在纵向、横向的二维空间上的演化过程[4]。
1 实验设计
1.1 试验装置
本实验装置的原理与达西渗流实验[4-6]相似,渗流速度的调节通过控制进出水端水头来实现,实验装置图1所示。为了能稳定水头供水,进水口采用水泵供水,排水出水口采用稳定溢流箱[7-8],在渗流槽内均匀布设18个观测孔,采用自主研发的多功能电导率在线检测仪进行实时监测。

1.2 土样选取
本实验选用了3种砂土,均取自松花江河底砂,将砂土筛分3次,筛分成细砂、中砂和粗砂,每次实验结束将砂土倒出进行冲洗,晒干后并重新装样[9-10]。
实验采用60 cm×30 cm的渗流槽,在渗流槽内装填高度为30 cm的砂土,因砂土粒径不同,所以密度也不一样。因此,参考经验容重,依据野外自然条件,3种砂土密度分别为:细砂1.5 cm3/g,中砂1.6 cm3/g,粗砂1.8 cm3/g,按计算值装填实验槽,每次装填1 cm的高度,并记录下所用砂的质量,装砂密度不均匀会造成实验偏差,如砂槽出现气泡或裂隙、密度不均,则需要倒出重装,保证槽内样品均匀,以满足实验要求。
经过多次实验,发现最适用于本实验的示踪剂是NaCl[11],并通过自主研发的电导值在线监测仪在线监测电导率,使实验中的测量精度得到了很大的提高,实验数据准确、真实、清晰地把握到在实验介质不同的情况下边壁渗流速度与非边界区域的差异。
2 实验结果及分析
2.1 参数计算
(1) 孔隙度。首先对粗砂、中砂、细砂的孔隙度进行计算,记录向槽内装砂的体积V以及砂体饱水时所注入水的体积Vn,如表1所示。通过计算得到粗砂、中砂、细砂孔隙度n分别为0.300 13,0.237 01,0.414 11。

表1 不同试验介质NaCl初始浓度
(2) 渗透系数求解。在水头差为4 cm条件下,对3种实验介质渗透系数进行计算。根据达西定律,通过计算得到结果如表2所示。

表2 3种不同介质的实验参数表
2.2 速度求解
为了探明边壁流效应对地下水渗流速度的影响,需将NaCl浓度转化成水流速度。经分析与推算,得到对流弥散方程[4,12-13]
(1)
式中:c为某一观测孔某一时刻NaCl浓度值;x为观测孔横坐标;t为某时刻时间;m为单位横截面积上瞬时注入示踪剂的质量;ω表示横截面积;n为试验介质的孔隙度;DL为弥散系数;u为渗流速度。
对于任意2个观测孔(如图1中1-1、2-1观测孔)在其浓度达到最大值时其对流弥散方程的导数为0,即c′=0,对c求导得:
(2)
整理得到:
代入2个观测点的x值和达到峰值的时间t值,得到关于u、DL的二元二次方程组,即可解得这2个观测孔之间的渗流速度,例如,代入中砂H=4 cm时数据,x1=22,x2=37,t1=130,t2=220,得到:
解得:u= 0.002 778,DL=0.000 937 257。
2.3 浓度曲线
由于实验室条件限定,NaCl浓度无法实时监测,在实验中示踪剂NaCl的浓度是通过测量NaCl的电导值而间接测得的。为了提高实验的测量精度以及数据的准确性,本实验采用电导值在线监测仪,通过布置的观测孔对NaCl的电导值进行测量,进而将电导值转换成浓度值[14-15]。为了得到电导率与浓度转化公式,在本实验NaCl浓度范围内取7组不同浓度进行实验,并测量它们的电导率值。将NaCl电导率作为横轴,NaCl浓度作为纵轴,得到NaCl浓度与电导率的相关直线,求得该直线相关系数R2=0.996,非常接近1,说明通过该直线求得的NaCl电导率与浓度转化公式正确,且可以使用[16]。该公式为:c=0.000 04S±0.003,其中,c为NaCl浓度;S为NaCl电导率;0.003为相对误差。
(1) 粗砂。在水头差4 cm条件下,将记录的电导值转化为浓度并绘制浓度曲线,通过曲线发现渗流槽边壁两侧NaCl浓度峰值出现时间早于中部NaCl浓度峰值出现时间。对第2列和第4列观测孔浓度达到峰值的时间比较发现:第2列中间孔相对两侧孔峰值出现的时间上滞后5 min(占总运移时间的6.31%),第4列中间孔与两侧孔的滞后8 min(11.57%),即溶质从第2列运移到第4列的过程中,两侧溶质要优先中间到达第4列。
图2为t=15 min时的浓度等值线图,从图中可以看出,渗流槽边壁NaCl浓度较中间要小。清楚地看到边壁流效应是存在的,而且对渗流过程影响很大。

图2 t为15 min的浓度等值线图
(2) 中砂。在水头差4 cm条件下,由于水流实际流速中等,使用与粗砂相同的方法计算NaCl浓度值,并绘制浓度曲线和sufer图。实验结果与粗砂相似,即渗流槽边壁两侧NaCl浓度峰值出现时间早于中部NaCl浓度峰值出现时间。
对第2列和第4列观测孔浓度达到峰值的时间比较发现:第2列中间孔相对于两侧孔的滞后时间为40 min(占总运移时间的6.00%),第4列中间孔与两侧孔的滞后时间为90 min(13.40%)。图3为t=280 min时的浓度等值线图。从图中可以看出,渗流槽中部示踪剂运移缓慢,发生堆积现象,而边壁两侧水流对NaCl运移则很快,更加清晰地反映出由于边壁效应的影响,渗流槽边壁渗流速度与中部速度有很大差异。

图3 t为280 min的浓度等值线图
(3) 细砂。在水头差4 cm条件下,水流实际流速较小,通过与粗砂、中砂实验相同的方法,记录NaCl电导率并计算NaCl浓度值。实验结果与中砂、粗砂相似,即渗流槽边壁两侧NaCl浓度峰值出现时间早于中部NaCl浓度峰值出现时间。
对第2列和第4列观测孔浓度达到峰值的时间比较发现:第2列中间孔相对于两侧孔的滞后时间为155 min(占总运移时间的5.17%),第4列中间孔与两侧孔的滞后时间为362 min(12.08%)。绘制浓度等值线图(surfer图),由图反映的现象与中砂基本一致。图4为t=2 800 min时浓度等值线图,图中直观地验证了边壁流效应的存在性。

图4 t为2 800 min的浓度等值线图
2.4 速度描述
按照式(1)、(2)计算速度值,对于每一行观测孔来说,有3或4个观测孔,为保证计算的准确性,任意2个观测孔都要计算其速度值,再取平均值,作为此行观测孔的渗流速度。不同种介质中每行平均渗流速度如表3所示。
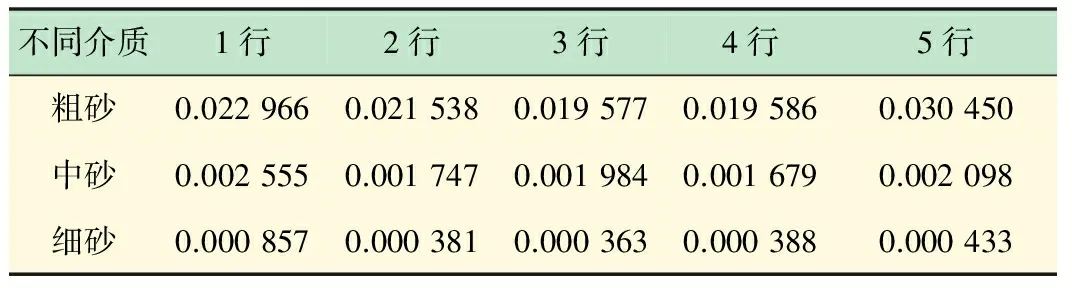
表3 3种砂中渗流速度每行平均速度表 cm/s


这样就可求得渗流槽中部水流速度相对于边壁两侧水流速度的滞后率。例如,对于粗砂而言,第1行速度为0.022 966,第5行速度为0.030 450,第3行速度为0.019 577。计算如下:
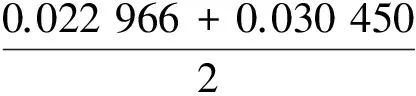

中砂、细砂中的滞后率计算方法与粗砂相同,滞后率计算结果为:粗砂26.70%,中砂14.72%,细砂43.72%。
比较渗流速度的滞后率,当水头差4 cm,实验介质不同时,渗流槽中部与边壁渗流速度滞后率为:细砂>粗砂>中砂。
3 结 语
通过对水力梯度为4 cm的不同实验介质渗流实验的研究,在浓度监测方面,发现渗流槽中部NaCl浓度总是小于边壁两侧浓度。由此在对渗流速度计算分析后,表明在水力梯度为4 cm的地下水渗流实验中,边壁两侧水流速度大于中部。同时,针对每组砂进行水力梯度分别为2、8、12 cm的若干组实验,也得到了相似的结果。
本次渗流实验验证了地下水渗流场中边壁流效应的存在,由于边壁流效应的存在,对渗流场边壁附近的渗透系数起到了增大的作用,对渗透流速起到了增益作用。因此,在水文地质实验中(如:地下水流速、流向测定实验,弥散实验,溶质或污染质运移实验等),观测孔的布设位置以及采样点的分布都要充分考虑边壁效应不可忽略的影响。
本文仅针对实验介质,定性地分析了不同实验介质边壁流效应之间的关系。对于两者之间定量关系,以及边界粗糙程度和水理特性对其影响程度则还需要进一步的实验。
[1] Boutt David F,Grasselli Giovanni, Fredrich Joanne T,etal.Trapping Zones : The effect of fracture roughness on the directional anisotropy of fluid flow and colloid transport in a singlefracture[J]. Geophys Res Lett, 2006, 33 (21) :L21402.
[2] 王 岩. 黄河口潮间带沉积物水及溶质优先迁移的试验研究[D].青岛:中国海洋大学,2010.
[3] Allaire Suzanne E, Roulier Stéphanie, Cessna Allan J.Quantifying preferential flow in soils: A review of different techniques[J]. Journal of Hydrology, 2009,378(2):179-204.
[4] 薛禹群,朱学愚,吴吉春,等.地下水动力学[M].2版. 北京:地质出版社,1997:3-66.
[5] Hincapié Ingrid, Germann Peter F.Impact of initial and boundary conditions on preferential flow[J]. Journal of Contaminant Hydrology, 2009, 104(4):67-73.
[6] 刘 凯,文 章,梁 杏,等.一维低渗透介质非达西渗流实验[J].水动力学研究与进展(A辑),2013,28(1):81-86.
Liu K, Wen Z,Liang X,etal. One dimensional low permeable medium non-darcy seepage experiment[J]. Chinese Journal of Hydrodynamics, 2013,28(1):81-86.
[7] 王锦国,周志芳.裂隙介质水流、溶质运移试验装置[P].中华人民共和国知识产权局专利.公告号:CN2699314Y,2005.
[8] 乔云峰.黄土中水盐运动实验研究[D].西安:西安理工大学,2001.
[9] 付宏渊,严志伟,李 海. 土柱溶质运移试验的理论验证及影响因素敏感性分析[J]. 长沙理工大学学报,2011,8(4):1-5.
Fu H Y, Yan Z W, Li H. Soil column test solute transport theory and influence factors sensitivity analysis[J]. Journal of Changsha University of Science & Technology, 2011,8(4):1-5.
[10] 贺玉龙,陶玉敬,杨立中.不同节理粗糙度系数单裂隙渗流特性试验研究[J].岩石力学与工程学报,2010,29(Sup. 1):3235-3240.
He Y L, Chen Y J, Yang L Z. Different joint roughness coefficient single fracture seepage experimental study[J]. Chinese Journal of Rock Mechanics and Engineering, 2010,29(S1):3235-3240.
[11] 李潇瀚. 基于试验及模型的冻融过程中水盐运移规律研究[D].长春:吉林大学,2013.
[12] 王秉忱,杨天行.地下水污染地下水水质模拟方法[M]. 北京:北京师范学院出版社,1985:12-43.
[13] 黄 琨. 孔隙介质渗流基本方程的探索[D].武汉:中国地质大学,2012.
[14] 魏新平, 王文焰,王全九,等.溶质运移理论的研究现状和发展趋势[J].灌溉排水,1998,17(4):58-63.
Wei X P, Wang W Y, Wang Q J,etal. Study tendency of soil solute transport as affected by irrigation[J]. Journal of Irrigation and Drainage,1998,17(4):58-63.
[15] 蔡金龙,周志芳.粗糙裂隙渗流研究综述[J].勘察科学技术,2009(4):18-23.
Cai J L, Zhou Z F. Review of seepage research in rough fracture[J]. Site Investigation Science and Technology,2009(4):18-23.
[16] 速宝玉,詹美礼,赵 坚. 仿天然岩体裂隙渗流的实验研究[J].岩土工程学报,1995,17 (5) :19-24.
Su B Y, Zhan M L, Zhao J. Study on fracture seepage in the imitative nature rock[J]. Chinese Journal of Geotechnical Engineering,1995,(17):19-24.
