UC安全的动态群组密钥协商协议设计与分析*

2014-02-09杨春尧陆正福

通信技术 2014年1期

关键词：群组结点攻击者

杨春尧,陆正福,李军

(1.成都卫士通信息产业股份有限公司,四川成都610041;2.云南大学数学与统计学院,云南昆明6500091)

UC安全的动态群组密钥协商协议设计与分析*

杨春尧1,陆正福2,李军1

(1.成都卫士通信息产业股份有限公司,四川成都610041;2.云南大学数学与统计学院,云南昆明6500091)

针对以往群组密钥协商限于孤立模型下讨论的问题,基于m叉树的判定Diffie-Hellman假设,使用通用可组合安全(UC安全)理论设计了一个群组密钥协商协议,并根据协议需要满足的安全目标,形式化地建立了协议的安全模型,通过对协议安全模块的设计和实现,证明了该协议满足UC安全性质。和同类协议相比,降低了密钥更新所需要的通信和计算开销,同时支持群组成员的动态加入和退出。

群组密钥协商 UC安全通信安全

0 引言

群组密钥协商(GKA,Group Key Agreement)协议在群组安全通信中具有重要的作用,因为它协商得到的密钥具有临时性,从而限制了密钥泄露事件带来的问题,常常被用于密钥泄露可能性高、复杂的环境中保证安全通信。

目前应用领域已经提出了一些GKA协议[1-2],这些协议的安全性分析都是在孤立模型中进行的,缺乏对并发环境下协议的安全性讨论,使得协议在并发运行时出现了许多设计时没有考虑到的缺陷。例如著名的Atenises-Steiner-Tsudik协议在提出之后3年才被发现存在并行会话攻击的漏洞[3]。究其原因,一方面固然是GKA协议的构造比较复杂、所需要考虑的安全因素比较多,但一个更为重要的原因是缺乏精准的安全模型和分析这些模型的理论工具。

为此,Canetti提出了通用可组合安全(UC安全,Universally Composable Security)理论[4]。根据UC安全理论,如果一个安全协议满足UC安全框架下的某些安全性质,则该协议和其他任何协议并发运行仍然能够保持这些安全性质。

文献[5]根据UC安全理论构造了一个GKA协议,该协议使用了签名理想函数作为参与者的身份认证接口,得到静态模型下基于二叉树的UC安全群组密钥交换协议(LTDH协议),但参与者之间的密钥关系采用的是线性二叉树,随着参与方人数增加,会使二叉树严重失去平衡,增加了下游结点的计算负担,导致协议的可扩展性较差。

文中在此基础上,采用了基于m叉树数据结构[6]的GKA协议,通过改变参数m来平衡成员关系树,较好地降低了关系树的高度。同时文中在UC理想函数中增加了群组成员的动态加入/退出的理想函数,并设计了一个子协议安全实现了该理想函数,最后通过UC安全组合定理,证明了文中所设计的群组密钥交换协议(m-TGDH协议)具有UC安全性质,其计算和通信效率好于LTDH协议。

1 理论基础

定义1(UC相似) 设φ,φ使两个协议,k为复杂度参数,用PPT表示所有概率多项式时间算法的集合,如果对任何攻击者A∈PPT都存在理想攻击者S∈PPT,使得对任何环境Z∈PPT和任何输入u其输出序列都是多项式时间不可区分的,即对任何判决器D∈PPT的优势函数:

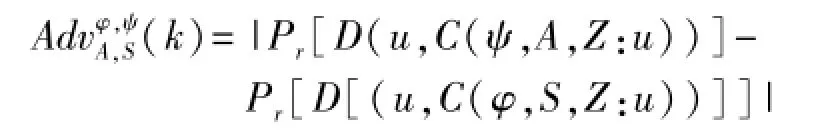
是关于k的一个速降函数,则称ψ与φ相似,记作ψ→UCφ。

定义2(协议独立性) 若协议ψ1的任何实例既不显式地、也不隐式地(例如,通过某则子程序或某个高层控制程序)访问协议ψ2的任何运行实例,同时ψ2对ψ1也有同样的性质,则协议ψ1和ψ2称为相互独立。若协议ψ与自身的任何运行实例之间从来不发生显式访问,也不发生隐式访问,则称协议ψ是自独立(subroutine-respective)的。

引理1(UC组合定理) 协议π(φ)是基于子协议φ的复合协议,协议φ和协议ψ都是自独立的,并且φ与ψ相互独立,若ψ→UCφ,则π(ψ/ φ)→UCπ(φ),其中π(ψ/φ)表示子协议φ和ψ组合后的复合协议[4]。

2 GKA协议的理想函数

UC安全模型下的协议的安全目标是由理想函数所刻画的,因此首先要定义GKA协议理想函数FGKA。设k为复杂度参数,P={M1,M2,…,Mn}为参与者集合,每个特定的FGKA实例都由一个唯一的sid标识,同时,该实例中对外部事务的请求标识为ssid。在通信过程中,假定群组成员的广播通信满足可靠性,则协议的理想函数描述如下。

1)初始化阶段:启动环境Z,当理想函数FGKA从参与者Mi收到消息(gkassion,sid,ssid,P,Mi)后,若该消息是第一次收到,则记录该消息,并将其转发给理想攻击者S,如果此时FGKA已收到|P|-1条此类消息,就将消息(Ready,sid,ssid,P)存储起来,同时转发该消息给理想攻击者S。

该阶段中FGKA刻画了理想攻击者S具有控制通信信道的攻击能力,因而可以截获FGKA发送给参与者的消息。

2)成员关系更新阶段:Mi向FGKA发送请求加入群组G的消息(Join,sid,Mi),FGKA把该消息转发给理想攻击者S,然后等待S响应,如果Mi获得S响应,FGKA就把Mi加入到群组中。如果参与者Mi向FGKA发送请求退出群组G的消息(Remove,sid,Mi),则FGKA把该消息转发给理想攻击者S,但不等S响应,FGKA直接将Mi从群组中删除。

3)密钥生成阶段:当理想函数FGKA从理想攻击者S收到消息(ok,sid,ssid,P)后,检查是否存在消息(Ready,sid,ssid,P),若存在该消息,则进行如下操作:

①若参与者集合P中任何一个参与者Mi都没有被理想攻击者完全控制,那么由FGKA生成群组会话密钥K←{0,1}k,保存消息:(SessionKey,sid,ssid,P,K)。

②若有某个参与者完全被理想攻击者控制,那么FGKA就等待S发送消息,接收到后保存为(SessionKey,sid,ssid,P,K)。

4)密钥广播阶段:当收到S发送的消息(Delivery,sid,ssid,Mi)时,FGKA检查是否存在消息(SessionKey,sid,ssid,P,K),同时检查Mi是否属于P的成员,如果两个条件都满足,由FGKA向Mi发送消息(SessionKey,sid,ssid,P,K),如果有一个不符合,则忽略该消息。

安全地实现理想函数是构造UC安全的群组密钥协商协议的关键。下面文中将构造实现FGKA的安全协议m-TGDH。

3 理想函数FGKA的安全实现

3.1 m-TGDH协议的模块化设计

对理想函数FGKA进行模块化设计可以简化协议的实现,文中对安全协议m-TGDH的实现分为三个模块(如图1所示)。

图1 GKA协议的UC组合模型Fig.1 UC Security model of GKA protocol

文中安全实现FGKA的思路是:首先构造一个安全实现签名理想函数Fsig的协议πsig;然后再构造一个安全实现群组成员关系理想函数Fset的协议πset;最后通过UC安全组合定理,在混合模型(Fsig,Fset, Fagent)上构造协议m-TGDH,证明协议在混合模型下安全实现了FGKA。

Fsig是文献[7]中提出具有UC安全性质的数字签名方案,用于对参与者的身份认证和抗消息伪造。

Fset理想函数是对群组成员加入和退出群组的一个抽象。

模块Fagent是用于描述用于提供在线认证功能但通信受限的理想函数。在文中的协议中,Mi能够使用该理想函数向CA机构提供Mi的公私钥对的合法性证明。

3.2 安全实现理想函数FGKA的协议形式化描述3.2.1 协议πsig的形式化描述

引理2设Sig=(gen,sig,ver)是能够抵抗选择密文攻击的签名方案,则在真实环境下,该协议对于静态攻击者可以安全实现Fsig,当且仅当Sig能抵抗选择密文攻击[7]。

由于可以抵抗选择密文攻击的签名方案容易得到(例如经过Fiat-Shamir变换得到的签名方案),所以由引理2可以构造安全实现理想函数Fsig。

3.2.2 协议πset的形式化描述

根据理想函数Fset的语义接口,文中将安全实现Fset的协议分再为两个子协议:成员加入子协议πset_J和成员离开子协议πset_R。

假设在t时刻,所有成员维护具有相同结构的m叉树。在这棵m叉树中每个叶子结点对应一个组成员Mi,hi为成员Mi在m叉树中的高度。在这棵m叉树中,首先由该组的第一个成员建立并选择具体的m叉树,并产生群组密钥。每个结点＜l,v＞有两个密钥:一个私有密钥K＜l,v＞和一个辅助密钥BK＜l,v＞,二者关系为:BK＜l,v＞=f(K＜l,v＞),其中f(k)≡gk(modp),g和p的取值来源于Diffie-Hellman协议。广播BK＜l,v＞,叶子结点密钥由Mi随机产生。

(1)成员加入协议πset_J的形式化描述

假设动态群组成员{M1,M2,…,MN},现MN+1请求加入群组,则协议的形式化描述如下:

1)MN+1向群组发送请求加入的消息(Jion,sid,P,Mi||ssid||Cert#MN+1)和其辅助密钥给{M1,M2,…,MN}。

2){M1,M2,…,MN}使用证书Cert#MN+1对MN+1的身份进行认证,若所有成员认证通过,则表示接受,负责表示拒绝。如果拒绝则停止该事务,否则进入下一步。

3)每个组成员调用以下算法更新m叉树:

①如果任取树的任意内部节点(l,v),度为TD (l,v)=m,按照层级遍历算法搜索深度最大且编号最小的的中间结点＜l,v＞,创建一个中间结点编号为＜l+1,mv＞,原来结点编号为＜l+1,mv＞的叶子结点变为＜l+2,mv2＞,新加入的结点变为＜l+2,mv2+1＞,否则转下一步。

②按照层次遍历算法搜索深度最大且编号最小且TD(l,v)＜m的中间结点＜l,v＞与深度最大且编号最小叶子结点＜l+1,mv+ni-1＞,新加入的群组成员MN+1编号为＜l+1,mv+ni＞。

(2)成员离开协议πset_R的形式化描述

假定群组中现在有N个成员P={M1,M2,…, MN},成员ML离开群组,则离开协议的形式化描述如下:

1)ML向群组中其它成员发送退出请求(Remove,sid,ssid,P,ML),Mi对ML进行检查:如果ML∉P则终止该事务,否则按照以下算法更新群组成员关系:

①离开结点M＜l.v＞的父结点为＜l-1,＞,按照层级遍历的来遍历m叉成员关系树。遍历编号最大的叶结点为发起者,否则次大的叶结点为发起者＜l′,v′＞。如果＜l,v+1＞为空,则＜l,v-1＞为发起者,如果＜l,v+1＞与＜l,v-1＞均为空,则＜l-1,m＞为发起者,否则停止。

②如果TD(＜l-2,v/m2＞)≥3,发起者＜l′,v′＞删除离开结点M＜l.v＞,并且令＜l′,v′＞=＜l,v＞,否则离开结点的兄弟结点M′提升父结点使得M′=＜l-1,＞。

2)发起者改变其私有密钥K与计算辅助密钥BK≡gKmodp,并将成员关系和辅助密钥广播到{M1,M2,…,MN}-{ML}。

3)所有组成员删除离开结点及其父结点,永久删除群组密钥,更新发起者的辅助密钥,并重新生成m叉成员关系树。

定理1如果群组成员的证书可以有效证实其身份的真实性,则协议πset安全地实现了理想函数Fset。

该引理的结论是显然的,因为从理想函数Fset和协议πset的描述可以看出,协议中安全更新成员的关系仅依赖于证书的存在。而每个成员的证书都可以通过密钥注册获得,因而该协议容易实现。

3.2.3 混合模型(Fsig,Fset,Fagent)下基于m叉树的m-GKA协议的形式化描述

当所有组成员维护好一棵m叉树后,开始协商通信所用的组密钥K=f(K＜0,0＞),其中f(.)为单向杂凑函数。m-TGDH协议的形式化描述如下。

1)设最深中间结点编号为＜l,v＞,则群组成员叶子结点编号为＜l+1,mv＞…,＜l+1,mv+ni-1＞。l+1层叶子结点Mi(编号为＜l+1,mv＞)调用伪随机函数Gen-Key(1k)产生结点密钥K＜l+1,mv＞,并计算BK＜l+1,mv＞=gK＜l+1,mv＞modp,向理想函数Fsig发送消息(Sign,sid,0| BK＜l+1,mv＞|ssid),Fsig返回签名值σi=SignSKMi(0| BK＜l+1,v＞|ssid)。Mi向Mi+1(其编号为＜l+1,mv+1＞)发送消息(Mi|0|BK＜l+1,mv＞|σi)。依此类推,编号为＜l+1,mv+j＞的成员Mi+j调用伪随机函数GenKey(1k)产生私有密钥K＜l+1,mv+j＞(j∈[0,ni-2]),并计算辅助

2)成员Mni-1(结点编号为＜l+1,mv+ni-1＞)把消息(Mni-1|0|BK＜l+1,mv+ni-2＞|σni-2)广播给编号为{＜l+1,mv+j＞|j∈[0,ni-1]}的所有结点。

3){＜l+1,mv+ni-1＞|j∈[0,ni-1]}中的结点成员＜l+1,mv+j＞向理想函数Fsig发送验证消息(Verify,sid,Mi+j,σj)。如果验证通过,则进行下面的操作,否则终止该事务。上述每个成员计算:

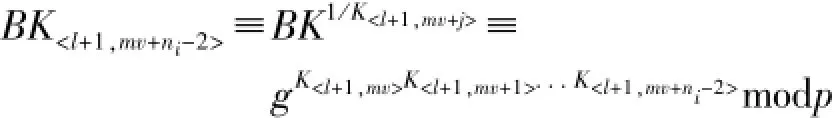
并对该消息签名后发送给Mni-1。

4)Mni-1调用伪随机函数GenKey(1k)产生私有密钥K＜l+1,mv+ni-1＞并计算集合:

S≡{)|∀j∈[0,ni-1]},之后向理想函数Fsig发送需要签名的消息(Sign,sid,1|S|ssid),得到理想函数Fsig的签名值σS=SignSKMni-1(1|S|ssid),并将消息(Mni-1|1|S|σS)广播给{＜l+1,mv+j＞|j∈[0,ni-1]}。

5)对于∀j∈[0,ni-1],Mi+j可以计算:

和辅助密钥BK＜l,v＞≡gk＜l,v＞modp。

6)K＜l,v＞和BK＜l,v＞为中间结点＜l-1,＞的子结点＜l,v＞的私有密钥和辅助密钥用于上层的子树结点＜l-1,＞的和的计算,递归调用步骤1)～6)直到计算出K＜0,0＞为止。

7)当组成员关系发生变化或者组密钥更新时间Δt到时,由与发生变化结点相邻结点Mi充当发起人,向理想函数Fset发送消息(Rekey,sid,ssid||Mi| |cert#Mi),所有组成员重新维护成员关系树。

4 m-TGDH协议的性质分析

4.1 协议的正确性证明

由于采用m叉树得到的密钥协商协议不同于GDH和基于2叉树的TGDH,其正确性不是显然的,下面采用数学归纳法对该协议进行证明。

证明:对树高H使用数学归纳法。当H=1时,协议就转化为一般的群组密钥协商(GDH)协议,并且群组至多有m个成员。当H≥2且m=2时,协议就变成TGDH协议;当H≥2且m＞2时,假定结点编号为:＜1,0＞,…,＜1,m-1＞则:

结点＜1,0＞产生随机私有K＜1,0＞,并计算其辅助密钥BK＜1,0＞≡gK＜1,1＞modp,并传送辅助密钥到结点＜1,1＞。

结点＜1,1＞产生随机私有密钥K＜1,1＞,并计算辅助密钥:BK＜1,1＞≡(BK＜1,0＞)K＜1,1＞≡gK＜1,0＞K＜1,1＞modp,并传送K＜1,1＞到结点＜1,2＞。依此类推,直到结点＜1, m-1＞计算出BK＜1,m-2＞,将其广播到群组集合:S={＜1,0＞,＜1,1＞,…,＜1,m-2＞}。

对于∀＜1,i＞∈S中的所有参与者计算(BK＜1,m-2＞)1/K＜1,i＞≡gK＜1,0＞K＜1,1＞…K＜1,m-2＞/K＜1,i＞modp,并发

送到结点＜1,m-1＞。结点＜1,m-1＞产生随机密钥K＜1,m-1＞,并对∀＜1,i＞∈S传送的密钥计算: (BK＜1,m-2＞)K＜1,m-1＞*1/K＜1,i＞≡gK＜1,0＞K＜1,1＞…K＜1,m-1＞/K＜1,i＞modp并将该密钥传送到结点＜1,i＞。对于∀＜1,i＞∈S计算:

位置为＜1,m-1＞的结点计算得到:

因而命题成立。

现假设当高度H＜h时,协议的计算是正确的,并且有每个叶子结点维护一棵m叉成员关系树。由上面的讨论可知,任意一个高度为H＜h的成员关系树,其每个成员都能计算出其祖先结点的私有密钥和辅助密钥。

当H=h时,由协议的密钥协商树的过程可知,每个群组成员都维护一棵相同的m叉成员关系树。在成员关系树的第1层,结点编号为＜1,0＞,＜1,1＞,…,＜1,m-1＞。以这些结点为根结点的每棵m叉成员关系树所具有层数至多为H=h-1,由递归假设可知,任意一个高度为H＜h的成员关系树,其每个成员都能计算出其祖先结点的私有密钥与辅助密钥,所以每个组成员均能计算出:＜K＜1,0＞,BK＜1,0＞＞、＜K＜1,1＞,BK＜1,1＞＞和＜K＜1,m-1＞,BK＜1,m-1＞＞。

因为每个叶子结点均知道第1层的结点的私有密钥的辅助密钥,根据群组密钥的计算过程,每个叶结点都能计算出:K＜0,0＞≡gK＜1,0＞K＜1,1＞...K＜1,m-1＞modp,因而协议是正确的。

4.2 m-TGDH协议的UC安全性证明

定理2如果通信受限的Fagent实例M能够以证据不可区分方式证明私钥的合法性,TDDH假设多项式等价于DDH假设,,则协议m-TGDH能够在混合模型中有(m-TGDH)→UCFGKA。

证明:在m-TGDH协议中,理想函数FGKA有三个模块Fsig,Fset,Fagent,则根据三者的定义,易知这三个理想函数是自独立的,并且两两之间相互独立。

记FGKEFset为FGKE去掉Fset后的理想函数,(m-TGDH)πset为去掉πset部分的协议,根据引理2,有(m-TGDH)πset→UCFGKEFset成立。由Fsig,Fset,Fagent三者的自独立性和两两相互独立性可知,FGKEFset和Fset之间、(m-TGDH)πset和πset之间也相互独立,根据定理1,有πset→UCFset成立,由UC组合定理得到(m-TGDH)→UCFGKA。

4.3 m-TGDH协议的性能分析

该协议的性能主要从计算开销、通信开销和存储开销三个方面进行分析。

通信开销:由于m-TGDH显著地降低了成员关系树的高度,GKA协议的通信开销主要依赖于成员关系树高度,其通信复杂度为O(nlogmn)。

计算开销:模幂运算是衡量计算开销的主要标准。在m-TGDH协议中,使用m叉树降低了成员关系树的高度,从而减少了中间结点的个数,有效降低了计算复杂度。因为logmn=logm2×lbn＜lbn,故该协议计算上的开销要低于LTDH协议。

存储开销:与TDH协议相似,m-TGDH协议的存储量也是O(n),但实际应用中,由于中间结点减少,其存储开销可能要略好与LTDH。

5 结语

文中利用UC安全框架对群组密钥交换协议进行了分析,进而提出了一个动态的群组密钥交换理想函数,并针对文献[5]中的LTDH协议的不足之处,使用m叉树设计了一个实现该理想函数的安全协议m -TGDH,并对协议的UC安全性作出了证明。经过对协议的性能分析比较,文中所设计的m-TGDH协议的性能要好于LTDH协议。文中采用的数据结构是m叉树,当成员加入、成员离开当成员关系变化时,所有组成员首先维护m叉树而把密钥更新放在群组密钥的协商阶段,其更新代价为O(logmn)。

[1]KIM Y,PERRIG A,TSUDIK G.Tree-based Group Key Agreement[C]//ACM Transaction on Information and System Security.New York:ACM Press,2004:60-96.

[2]陈廷威,高博.一种基于服务端的群组密钥协商方案[J].通信技术,2010,43(03):162-164.

CHEN Ting-wei,GAO Bo.A Key Agreement Scheme based on Servers Group[J].Communications Technology, 2010,43(03):162-164.

[3]PERERIA O,QUISQUATER J.Some Attacks on Authenticated Group Key Agreement Protocols[J].Journal of Computer Security,2003,11(04):555-580.

[4]CANETTI R.Universally Composable Security:A New Paradigm for Cryptographic Protocols[EB/OL].http:// eprint.iacr.org/2000/067.pdf

[5]贾洪勇,卿斯汉,谷泽利,等.通用可组合的组密钥交换协议[J].电子与信息学报,2009,31(07):1571-1575.

JIA Hong-yong,QING Si-han,GU Li-ze,et al.Universally Composable Group Key Exchange Protocol[J]. Journal of Electronics&Information Technology,2009,31 (07):1571-1575.

[6]陆正福,何英.组密钥管理中d叉树数据结构设计[J].计算机工程与科学,2006,28(10):13-15.

LU Zheng-fu,HE Ying.Design of d-ary Tree Structure for Group key Mangement[J].Computer Engineering& Science.2006,28(10):13-15.

[7]CANETTI R.On Universally Composable Notions of Security for Signature,Certification and Authentication [M].New York:ACM Press,2003.

杨春尧(1986—),男,硕士研究生,主要研究方向为密码编码学、密码协议;

YANG Chun-yao(1986-),male,graduate student,majoring in cryptography and cryptographic protocols.

陆正福(1965—),男,教授,主要研究方向为密码编码学、安全多方计算;

LU Zheng-fu(1965-),male,professor,mainly engaged in cryptography and SMC.

李军(1974—),男,工程师,主要研究方向为信息安全。

LI Jun(1974-),male,engineer,mainly working at information security.

Design and Analysis of Dynamic Group Key Agreement Protocol with UC Security

YANG Chun-yao1,LU Zheng-fu2,LI Jun1
(1.Chengdu Westone Information Security Industry Co.,Ltd.,Chengdu Sichuan 610041,China; 2.School of Mathematics and Statistics,Yunnan University,Kunming Yunnan 650091,China)

Aiming at the fact that the concurrent group key agreement(GKA)protocol is discussed only within the isolate model,and based on m-ary tree decisional Diffie-Hellman within the framework of universally composable(UC)security,a group key agreement protocol is designed,and the ideal functionality model for GKA protocol formulated.The security modular design and implementation of GKA protocol indicates that this protocol could meet the requirement of UC security.Compared with the similar protocol of GKA,this new protocol has the advantages of less communication and computation overhead,while supports group members in their dynamic joining and exiting.

group key agreement;universally composable security;communication secrutiy

TP393

1002-0802(2014)01-0081-05

10.3969/j.issn.1002-0802.2014.01.016

国家自然科学基金资助项目(No.10861012)

Foundation Item：NSFC(No.10861012)