Study of simple plane wave generator with an air-metal barrier

Wei XIONG,Xin-feng ZHANG,*,Zhong-wei GUAN,Yong HE,Ling QIAO,Li-li GUO

aSchool of Mechanical Engineering,Nanjing University of Science&Technology,Nanjing 210094,Jiangsu,China

bSchool of Engineering,University of Liverpool,Brownlow Street,Liverpool L69 3GQ,UK

cBeijing Institute of Space Long March Vehicle,China

1.Introduction

Due to the requirements of the material processing and research on dynamic behavior of materials,the acceleration of high velocity projectiles[1-3]and various methods to obtain a plane wave[4-10]using high explosives have been studied in recent years.Plane wave generator(PWG)is a common explosion apparatus to generate a plane wave by controlling detonations of high explosive(HE)charges.The typical configurations of PWGs include two-component explosives,multipoint initiation,mouse trap and inert materials[4-10].The two-component-explosive PWG,i.e.,explosive lens,which consists of two explosives with different detonation velocities,was considered to be the most efficient way to generate plane waves[7,8].This kind of PWG has been most widely used,however the corresponding fabrication processes and the control of detonation waves are difficult because of its complicated structures.Additionally,it is expensive.

In order to obtain simplified fabrication processes,a lower cost,and a plane wave with higher precision,there is a trend to replace the explosive with an inert material in the central wave-shaping mechanism.Sandia National Laboratory in USA manufactured a small-size PWG using brass as an inert material,in which the time difference of detonation wave generated can be less than 0.245μs in the range of φ20 mm[9].Besides,plexiglass as an inert material was also studied by Chen et al.[4].and Fritz[10].The inert material can be produced by casting,which makes the fabrication process more conveniently with a smaller demand for charge.Additionally,the detonation waves generated by the PWGs with inert materials are more planar and more easily controlled.

Generally,most of the above studies were concentrated on the curve surfaces of the inert explosives or materials.However,the fabrication would be simpler if the curve surface of the inert explosive or material could be replaced by a plane surface.Therefore,in order to design a simpler structure and obtain more plane waves,a simple plane wave generator with air-metal barrier was studied[11,12].

The simple plane wave generator is composed of two cylindrical charges and an air-metal barrier between them,as shown in Fig.1.An important effect of the barrier is that a transmitted shock wave can be formed at the explosive-metal interface and then propagates in the metal media.On the other hand,when the spherical detonation waves are in contact with air,the detonation products expand at high pressure and velocity.Therefore,the main charge is initiated either by the shock wave or the detonation product.Since the velocity of a shock wave formed in metal is higher than that of detonation products expanding in air,the configuration of detonation waves is changed.Based on the above analysis,a spherical detonation wave can be adjusted to a quasi-plane wave.

Fig.1.Schematic diagram of a simple plane wave generator.

Aluminum is suitable for metal part due to its low density and high sound velocity.The simple plane wave generator with an aluminum ring was first designed by Yu and his colleagues[11],and the detonation waves with high flatness generated by the device were measured in their experiments.However,an important factor to the high flatness might be a large slenderness ratio(about 2)of charges used in their experiments,which would increase the curvature radius of the spherical wave and make it approximate to a plane wave.Zhao et al.[12]also designed a simple plane wave generator,in which the slenderness ratio of the HE charge is 0.6.The device was used in the test of the dynamic constitutive relationship of granite specimens.However,there have been few studies on the theoretical model and specific design method in the publications.

The objective of this paper is to design a simple plane wave generator with aluminum ring,in order to obtain more plane waves.Theoretical analysis and numerical simulations were both presented to determine structure parameters of this kind of PWG.The specific theoretical analysis is concentrated on two kinds of interfaces mentioned above,one is between the aluminum medium and explosives,and the other is between the air gap and explosives.Consequently,the size of aluminum ring can be calculated for a given charge.The numerical simulations were carried out by AUTODYN®with Lee-Tarver and JWL model based on the theoretical calculated results.Time difference was used to evaluate the flatness of detonation waves.The results provide the difference in generated detonation waves based on different sizes of aluminum rings.In addition,the simple PWG with an air-metal barrier can be designed for given charges.

2.Mathematical description of simple PWG with an airmetal barrier

In order to determine the size of an aluminum ring for a given charge,the propagation of the detonation wave in the PWG with an air-metal barrier was analyzed.Fig.2 shows two different propagation paths of a detonation wave or a shock wave,i.e.i→ o→ f and i→ a→ e.Here,OA,OB and OR are the detonation wave front,the transmitted shock wave front and the reflected shock wave front at the explosive-metal interface,respectively.Considering the disturbance of the outside rarefaction wave at the edge of the barrier and the complicated interactions at the aluminum-air interface in the barrier,for simplification,only the middle Point“o”of the bc segment is focused.On the other hand,the propagation path of a detonation wave from “i”to “a”in the secondary charge is the shortest.Thus,a quasi-plane wave can be obtained if the total time for the wave to travel along the two paths is equal.

2.1.Analysis of shock waves via the aluminum media

Assuming that the detonation is in a steady state after initiation and based on the geometric relation shown in Fig.2,the time required for the detonation wave to arrive at point“o”is

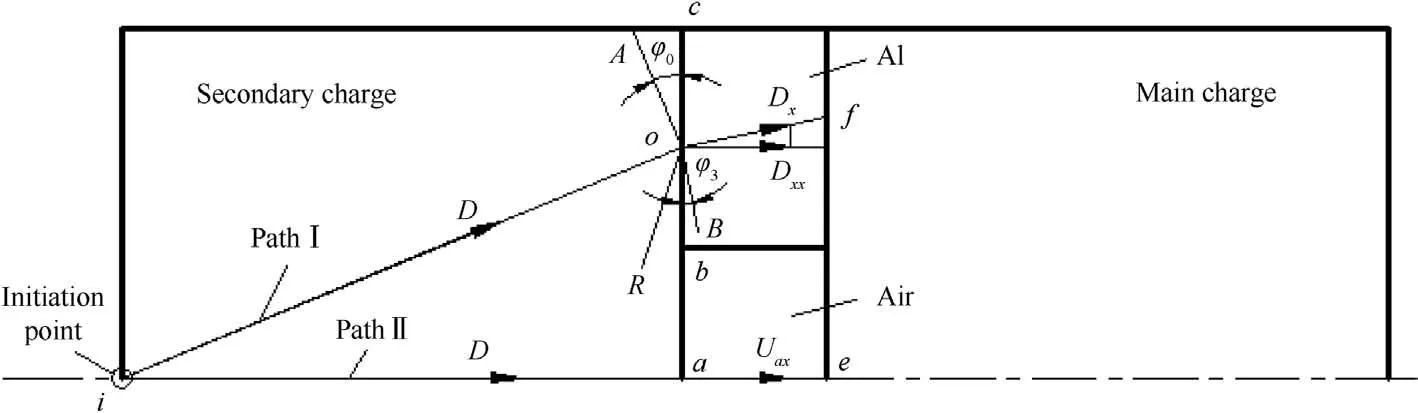
Fig.2.Schematic diagram of the function principle.

where D is the detonation velocity;φ0=arctan（dE+dA/4L）is the incident angle of detonation wave;L and dEare the length and diameter of explosive cylinder,respectively;and dAis the inner diameter of aluminum ring.

With the impact of the oblique detonation wave at the interface,in which the peak pressure may reach several billion Pa,a transmitted shock wave is formed.First of all,it is important to determine the initial parameters of the transmitted shock waves.According to the theory of oblique detonation waves in Refs.[8],the angle φ3between the interface and the transmitted shock wave front can be determined and then the initial shock velocity Dmin the aluminum can be defined as

Furthermore,the initial parameters of the transmitted shock waves,such as shock pressure pm,media density ρmand particle velocity um,can be determined according to the mass conservation equation,the momentum conservation equation and the equation of state(EOS)of media,respectively

where ρm0is the initial density of media;and C and S are the constants in EOS.For aluminum,ρm0equals 2.785 g/cm3,C equals 5.328 km/s,and S equals 1.338.

Then,according to Ref.[14],an exponential decay relationship of the pressure versus distance can be used to describe the propagation of a shock wave through elastic-plastic material at the segment of

where pxis the pressure after the shock waves propagates for x mm in the media;and α is the corresponding attenuation index.For aluminum,α=0.047 mm1[14].

According to Eq.(4)and Eq.(5),the corresponding shock velocity Dxin the media can be defined as

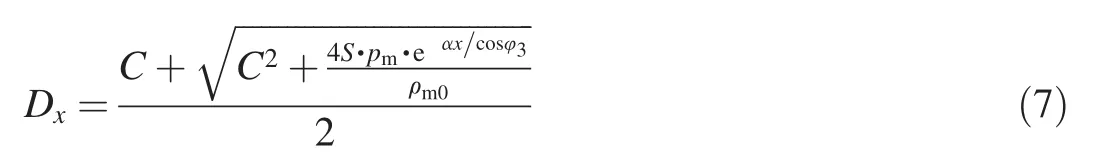
Thus,the time for shock waves to propagate through the media is

where l is the thickness of the air-metal barrier.

Finally,according to Walker's and Wasley's work[15],the critical energy Ecper unit area for shock initiation of heterogeneous explosives can be defined as Ec=puτ,where p and u are the pressure and particle velocity of shock waves in explosives,respectively,and τ is the time for initiation.Thus the time for a shock wave to initiate the main charge is

where pfand ufare the pressure and particle velocity of the transmitted shock waves in HE at Point “f”,respectively,which can be determined by a graphic method with Hugoniot curves[16].Additionally,it should be point out that the propagation distance of shock waves in the main charge during this process was neglected since the initiation time is too short.

Based on above analyses,the total time for the wave to travel along Path I is

2.2.The effect of air gap on detonation products

Similarly,the arrival time of detonation waves at Point“a”is The pressure decreases with the expansion of detonation product in the air.For the simple PWG,the thickness of the aluminum ring is much less than the length of the secondary charge.And for common spherical charges,according to the formation process of air blast wave in Ref.[13],the corresponding expansion of detonation products at such a small air gap can be described as

where pHand VHare the pressure and volume at C-J state,respectively;paxand Vaxare the pressure and volume of detonation products during expansion,respectively.It can be proved that no air blast wave is formed in this process.

However,the calculation results based on this law is proved to be quite different from the simulation results in the Comp B by AUTODYN-2D®,as shown in Fig.3.It can be see from Fig.3 that the initial pressure obtained from the simulation is only one eighth of the C-J pressure in explosive.And the pressure paxand the particle velocity uaxof detonation products during expansion can be redefined as

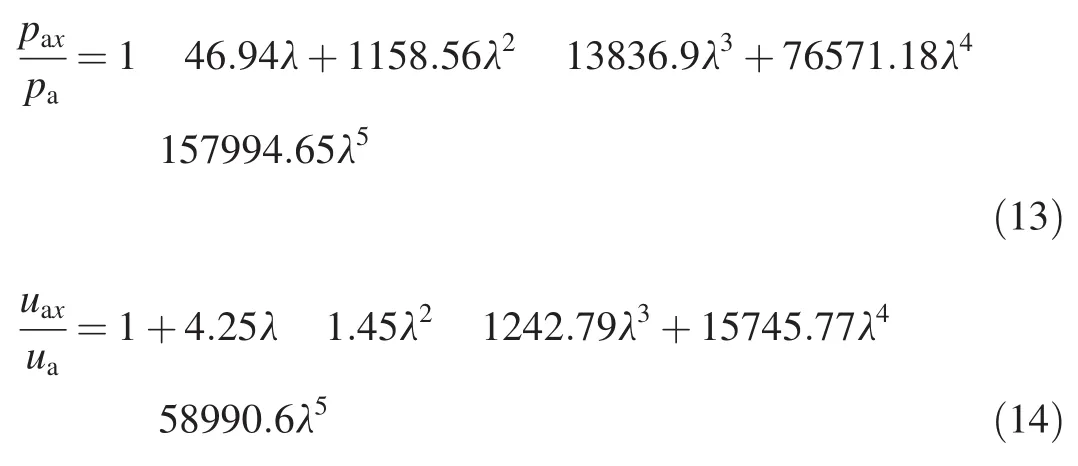
where paand uaare the initiate pressure and velocity of detonation products, respectively. pa= 3.32 Gpa,ua=4067 m/s,λ=x/(L+x),and x is 0-10 mm.

Thus the time for the expansion process of detonation products in the air gap can be expressed as

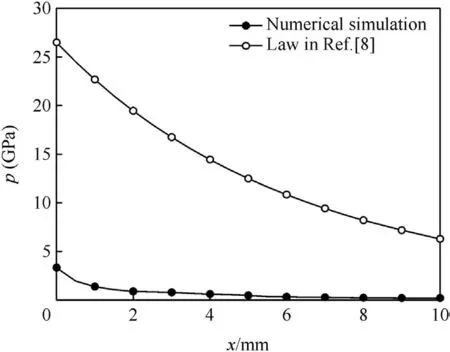
Fig.3.Comparison of the simulation results with(φ50?50)mm Comp B and the calculation results with the same charge based on the law in Ref.[8].

The impact of detonation products against the main charge can be described as an impact between different materials in Ref.[15].The corresponding time for shock initiation is

where peand ueare the pressure and particle velocity of the transmitted shock waves in explosive at Point “e”,respectively.

Therefore,the total time for the process along the Path II is

2.3.Theoretical calculations of the simple PWG with air-metal barrier

Based on the theoretical analysis above,it shows that the ultimate shape of the detonation wave in the main charge is determined by the parameters related to the charge and the airmetal barrier.After obtain the calculation results by analyzing through two different paths,it becomes easier to design the simple PWG with an air-metal barrier.

Calculations were performed for some typical schemes shown in Table 1,where the charge was given,and the inner diameter of the aluminum ring was set to be little less than the half radium of the explosive.The total time for the wave totravel along the two paths depends on the thickness of the aluminum ring,which can be obtained through calculations.The parameters of charges are given in Table 2.The time--thickness curve for each scheme is shown in Fig.4.Additionally,some calculation parameters at the Point P for the first scheme and the third scheme are shown in Table 3.

Table 1Parameters of typical schemes.

Table 2Parameters of charges.

The abscissa of intersection point P of each scheme in Fig.4 indicates the value of the optimal thickness of aluminum ring for generating a quasi-plane detonation wave.The results show that the thickness of aluminum ring in Comp B is different from that in RDX with comparison of Schemes 1 and 3.It is mainly due to the higher detonation velocity of RDX,which decreases the time difference in the secondary charge.Besides,the detonation pressure and critical energy for a shock initiation of an explosive are also very important factors.

On the other hand,it can be seen from Fig.4 that the calculation results vary from the size of the secondary charge or the inner diameter of aluminum ring,which have an important influence on the propagation distance and incident angle φ0.

3.Simulations of detonation wave in the simple PWG with air-metal barrier

In order to verify the validity of the theoretical model and show the propagation process of detonation wave in the simple plane wave generator,the numerical simulations based on the calculation results were conducted using AUTODYN-2D®,where the HE was modeled as Comp B with size of(φ50?50)mm.Additionally,a nylon shell was added to the charge to prevent the outside rarefaction wave from disturbing.

In the simulation,the nylon shell was modeled as Lagrangian meshes,while the propagation process of detonation waves or shock waves in the HE and the aluminum ring were described by Euler algorithm.The Euler grid,modeled as a rectangle(300?120 mm),was sufficiently large enough to cover the entire structure.The nonreflecting boundary condition was added on the side surfaces of the Euler domain.

A regular mesh of 0.5 mm square cells was used.The hydrocode model is shown in Fig.5.In the simulation of shock waves,the element size is important[17].A coarse mesh will induce the dispersion effects and lead to the inaccurate results.Therefore,an upper limit is set for the element size in order to properly simulate the shock waves.On the other hand,an increase in cell resolution decreases the time step and increase the calculation time.Several simulations were conducted,which proved that the cell size has little effect on the result if it is less than 0.4 mm.

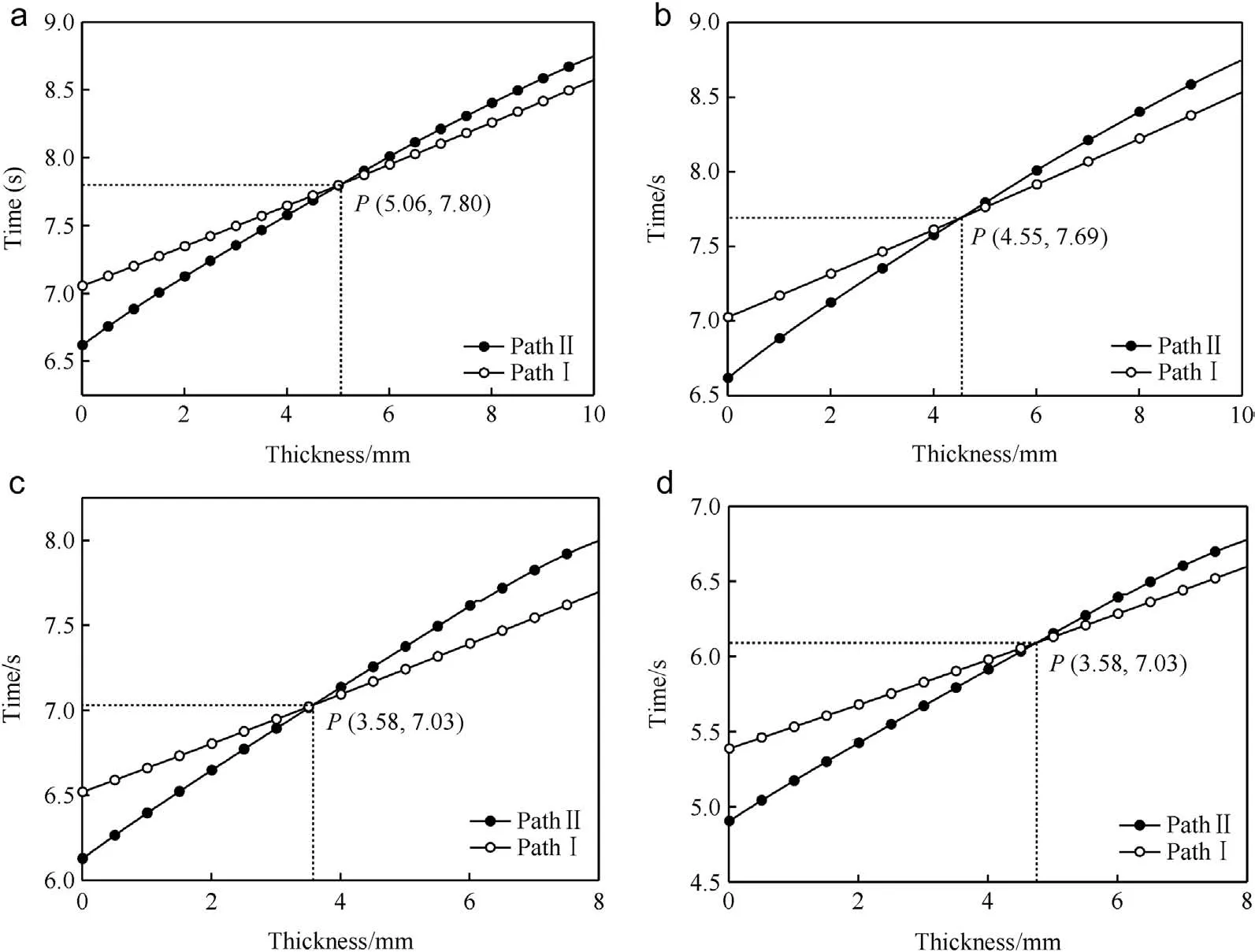
Fig.4.Theoretical calculation results for 4 typical schemes.(a)Comp B,dE=50 mm,L=50 mm,dA=22 mm(b)Comp B,dE=50 mm,L=50 mm,dA=19.5 mm(c)RDX,dE=50 mm,L=50 mm,dA=22 mm(d)RDX,dE=50 mm,L=40 mm,dA=22 mm.

Table 3Calculation parameters at Point p.

Fig.5.Numerical simulation model of the simple PWG.

In order to simulate propagation processes of a detonation wave and a shock initiation,the JWL model was used in the secondary charge,while Lee-Tarver model was used in the main charge.Additionally,the shock responses of other materials were modeled using the Mie-Grüneisen equation of state(EOS).The metal constituent of barrier was modeled as Al 2024 with the Steinburg Guinan constitutive model.The main parameters of all materials are shown in Tables 4-6.

Table 4Parameters of JWL for Comp B.

Table 5Parameters of Lee-Tarver model for Comp B.

Considering the influence range of an impact initiation and the interaction between transmitted shock waves in the main charge,a series of Gauss points were set at the plane with a distance of 15 mm from the interface of the main charge and the radius increment of 3 mm.The time difference of a detonation wave to arrive at each point was calculated,which can be taken as a criterion to judge the flatness.

The size of the aluminum ring was adjusted around φ(50-22)mm?5.06 mm based on the theoretical calculations,the results of several simulations are shown in Table 7.The percentages of 70 and 60 represent the measured range,e.g.70%is 70-percent diameter of the main charge,in other words,the measured diameter is 35 mm.

Table 6Parameters of aluminum and nylon.

Table 7Time difference of several typical schemes.

By comparing the data in Table 7,it is easy to find out that the flatness of the detonation wave is clearly improved after an aluminum ring is added.The comparison of the first five sets of the data shows that the flatness of detonation wave changes with the size of the ring.Thus,it is necessary to design the optimal size of aluminum ring so that a satisfactory flatness of the wave can be obtained.The aluminum ring with the size of φ(50-22)?5.1 mm is proved to be the optimal one with the highest precision to generate a plane wave.Additionally,the time difference increases with the measuring range due to the disturbance of rarefaction wave.

Clearly,the configuration of the detonation wave measured in Scheme 1 is far inferior to that of others.Without theoretical calculations,tens of more models need to be used for the simulations in order to obtain the optimal result.Therefore,a theoretical analysis,as a valid reference,can be used to reduce the workload of the numerical simulations.

The pressure nephogram of different simulations can be used to show the shape of a detonation wave in a more intuitive way.It can be seen from Fig.6 that the detonation wave generated in PWG is much planar than the spherical detonation wave only in a long cylindrical charge.

Additionally,the functional process of PWG can be observed from the pressure nephogram in Fig.6(a).It is obvious that the initial shape of the detonation wave is spherical.The expansion of detonation products in air and the shock waves in the aluminum media can be seen at 7μs.Finally,a quasi-plane wave can be observed at 12μs.

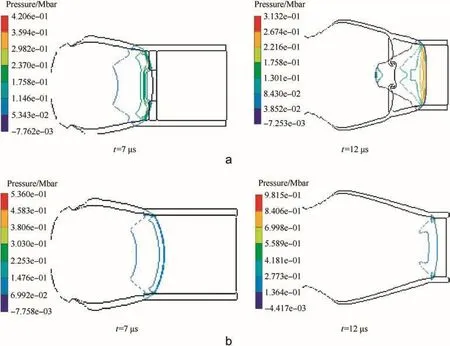
Fig.6.The shapes of detonation waves at different times.(a)Withφ(50-22)?5.1 mm aluminum ring(b)Without aluminum ring.

4.Discussion

The theoretical model for the simple PWG with air-metal barrier in Section 2 is essentially based on the following three assumptions:

1)The disturbance of the rarefaction wave outside can be neglected.

2)The parameters of detonation products in expansion are defined by means of numerical simulations.

3)The propagation distance of shock waves in the main charge during this process can be neglected.

The first assumption is based on that the disturbance of the rarefaction wave outside can be reduced by a shell.The second assumption is based on the fact that no appropriate model has been established to describe the initial expansion of detonation products.The final assumption is based on the current calculations,in which the time for shock initiation is ten-thousandth of that for the whole process.

Compared with other types of PWGs,the advantages of the simple PWG studied in this paper are listed as follows:

1)A cylinder structure and a plane surface are used to replace the conic structure and the curve surface,which makes the design and fabrication process relatively easily.

2)A detonation wave with a flatness of 0.039μs within the range of 70-percent diameter of the main charge can be obtained,which produces a good flatness.

Although the simple plane wave generator with an air-metal barrier has been designed based on the theoretical analysis and numerical simulations,the following remarks need to be pointed out.

1)In the theoretical model,the propagating process of detonation wave at explosive-media interface is analyzed at its central point for simplification.However,the whole process is actually more complicated,especially at the air-metal interface.Besides,the aluminum ring thickness(5.06 mm)predicted by analytical model is less than that from the simulation calculations.The reason is that the detonation is regarded as instantaneous,in which the detonation velocity is steady after initiation.In fact,it is lower than C-J velocity before its steady state.Thus,the theoretical calculations only provide a reference for the design of this kind of PWGs.

2)The proposed model presents a methodology to design the simple PWG with an air-metal barrier.However,only limited data are available in literature that give the comparison between the above calculated results and the experimental data.More experimental work needs to be carried out to validate the results calculated.

5.Conclusions

In this paper,a simple plane wave generator was designed by means of theoretical analysis and numerical simulations,and the optimal size of the air-metal barrier was determined.The theoretical analysis can provide a reference and reduce the workload of the numerical simulation.The major conclusions can be summarized as follows:

1)Two different propagation paths of the waves were discussed in the theoretical model.A detonation wave performs differently when it contacts with metal and air.

2)The numerical simulations based on the calculation results were conducted,where a detonation wave with a flatness of 0.039μs within the range of 70-percent-diameter was obtained by using an aluminum ring with a size of φ(50-22)?5.1 mm.

3)The plane wave generator with an air-metal barrier is a good flyer accelerating device,by which a plane wave with high precision can be obtained using a simple structure.

Acknowledge

The research sponsored by the National Natural Science Foundation of China(NSFC10902053),the Zijin Intelligent Program,Nanjing University of Science and Technology(2013_ZJ_0101),Qing Lan Project of Jiangsu province and the Fundamental Research Funds for the Central Universities(No.2012XQTR006).The authors would also like to thank the State Key Laboratory of Explosion Science and Technology(Beijing Institute of Technology)(KFJJ15-07M)for their great support on the research work presented in this paper.

[1]Crozier WD,Hume W.High-velocity,light-gas gun.J Appl Phys 2004;28(8):892-4.

[2]Seigel AE.The theory of high speed guns.Advisory Group for Aerospace Research and Development Neuilly-sur-Seine(Franch);1965.

[3]Lexow B,Wickert M,Thoma K,Schafer F,Poelchau MH,Kenkmann T.The extra-large light-gas gun of the Fraunhofer EMI:applications for impact cratering research.Meteorit Planet Sci 2013;48(1):3-7.

[4]Chen CY,Shiuan JH,Lan I.Design of an inert material type plane wave generator.Propell Explos Pyrotech 1993;18(3):139-45.

[5]Bernstein D,Goettelman RC.Generation of cylindrically symmetric implosions.Rev Sci Instr 2004;37(10):1373-5.

[6]Benedick WB.Detonation wave shaping.Albuquerque,N.Mex.:Sandia Labs;1972.

[7]Crutchmer JA.Slow PBX and plane wave lens development.Progress Report,July-September 1975.Amarillo,Tex.(USA):Mason and Hanger-Silas Mason Co.,Inc.;1975.

[8]Yadav HS,Kamat PV,Sundaram SG.Study of an explosive-driven metal plate.Propell Explos Pyrotech 1986;11(1):16-22.

[9]Vigil M.Plane shock generator explosive lens;1994.

[10]Fritz JN.A simple plane-wave explosive lens.NM(USA):Los Alamos National Lab.;1990.

[11]Yu DY,Xu WX,Zeng XF,Xu K.A simple plane detonation wave generator.Explos Shock Waves 1982;2:81-2.

[12]Zhao HP,Ye L,Zhao RB,Lu ZQ.The experimentation of simple plane or line wave generators.Explos Mater 2005;34(3):1-5.

[13]Zhang BP.Chinese book of explosion and its effects;1979.pp.240-60.

[14]Wang HF,Feng SS.An approximate theoretical model for the attenuation of shock pressure in solid materials. Acta Armamentarii 1996;17(1):79-81.

[15]Walker FE,Wasley RJ.Critical energy for shock initiation of heterogeneous explosives.Lawrence Livermore Laboratory:University of California;1968.

[16]Meyers MA.Dynamic behavior of materials.New York:John Wiley&Sons;1994.pp.110-201.

[17]Zhang CS,Zou DH,Madenga V.Numerical simulation of wave propagation in grouted rock bolts and the effects of mesh densityand wave frequency.Int J Rock Mech Min Sci 2006;43(4):634-9.