Research on the fracture behavior of PBX under static tension

Hu GUO*,Jing-run LUO,Ping-an SHI,Jian-guo XU

Institute of Systems Engineering,China Academy of Engineering Physics,Mianyang 621900,China

1.Introduction

Polymer bonded explosive(PBX)is a heterogenous explosive consisting of a mixture of crystalline particles and polymer binders.This kind of explosive is pressed from molding powder and could be classified by different components and their contents.In weapon system,PBX with some structure is always an important part,and the initiation is the main function of PBX structure.In order to insure the safety and reliability of weapon system during storage,transportation and use,PBX structure must provide sufficient mechanical property[1].PBX is a highly filled composite material comprised of more than 90%of crystals(by volume),which brings challenges to study its mechanical behavior.In general,the modulus of the binder is 105times lower than that of the crystalline particles,resulting in the mechanical behavior of PBX being heavily influenced by the properties of the binder.The mechanical response of PBX is known to be with very low tensile strength relative to its compressive strength,which makes PBX structure one of the weakest parts in weapon system.With the improvement of weapon safety assessment requirements,the research on fracture behavior of PBX is becoming more and more important.

It is an effective approach to study the fracture behavior of PBX by establishing a microscopic model,especially for the study of fracture mechanism.The establishment of microscopic model is difficult since the crystalline particles possess irregular shapes and different sizes.Biswajit Banerjee[2]proposed a recursive cells method(RCM),in which the representative cell is divided into many sub units,and calculated by stepwise iteration method.The effective elastic modulus of PBX was calculated through this method.This method could exhibits the high filling of crystals,nevertheless,the irregularity of shapes and random sizes could not be characterized.Li Jun-ling[3]established a microscopic model of PBX disc specimen using discrete element method(DEM),and simulated the failure process of PBX disc under diametral compression.DEM is more favorable than FEM in the simulation of fracture behavior,but costs more memory and time.Wu Yan-qing[4]built a microscopic model based on Voronoi model,and simulated the interfacial debonding of particles using a viscoelastic constitutive model,but the microscopic model was not periodic.

In this paper,we shall construct a two-dimensional representative volume element(RVE)based on Voronoi model in which the component contents could be regulated and particles are randomly distributed.A nonlinear damage model of polymer matrix relative to matrix depth between particles is employed.Through finite element method,the fracture behavior of PBX under quasi-static tension is simulated and the effects of initial damages are studied.

2.Finite element implementation

2.1.Representative volume element establishment

The original concept of Voronoi model is from the domain of computing geometry.Since the concept of Voronoi model was proposed by Dirichlet in 1850[5],Voronoi model has been applied to a few areas.It is well used to simulate the process of crystallization.

The ultimate principle of Voronoi model is to seek the nearest domain Siof reference point Pi.Voronoi model with two and six reference points are shown in Fig.1.In computing geometry,the construction of two-dimensional Voronoi diagram could be described with a formula.If there is a point set P with n reference points in a plane,namely P= ｛P1，P2，…，Pn｝,the domain Sicould be defined by the formula below

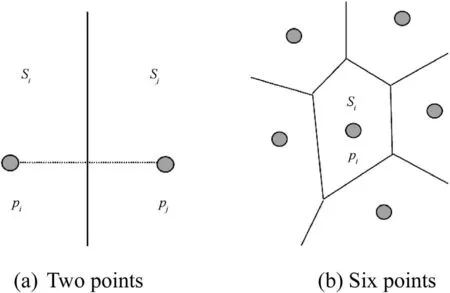
Fig.1.Schematic diagram of Voronoi model with different amounts of reference points.

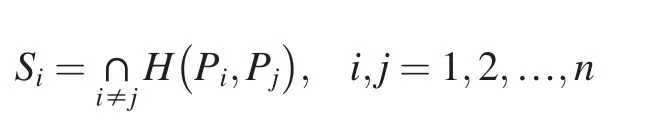
where H（Pi，Pj）is a plane domain about reference points Piand Pj,every point in this domain is nearer to Pibut to Pj.

As described above,Sidenotes a half plane for n=2,Sidenotes the intersection of n-1 half planes for n≥3,and Sidenotes a convex polygon with n-1 edges for n≥4.If the reference point set is determined,the corresponding Voronoi diagram is definite[6],so the Voronoi diagram could be controlled by the corresponding reference points.In this paper,a Voronoi model which is periodic and random was constructed by controlling the reference points.As shown in Fig.2,a plane box A is given in the size of 3L×3L,where L is a scalar.Box A is divided into 9 sub-boxes,each of which is L×L.The sub-box in the middle is sub-box B.First,the reference points are seeded in sub-box B randomly,and then they are copied into the other 8 sub-boxes.The distance between two points in sub-box B is controlled by a parameter ηin case a quite small polygon cell is generated.The polygon cell with small size has little effect on simulation result,but increase the computing cost obviously.At last,a definite Voronoi diagram is generated by the reference points in Box A.All the processes above are implemented in Matlab software.As shown in Fig.2,a cell in the size of L×L which is cut out arbitrarily from the Voronoi diagram is periodic.The periodic cell is called a Voronoi cell here.In a Voronoi cell,there must be a point on a boundary line corresponding to the other point which is on a boundary line,too,like Q and Q′.The coordinates of points Q and Q′follow the relation below

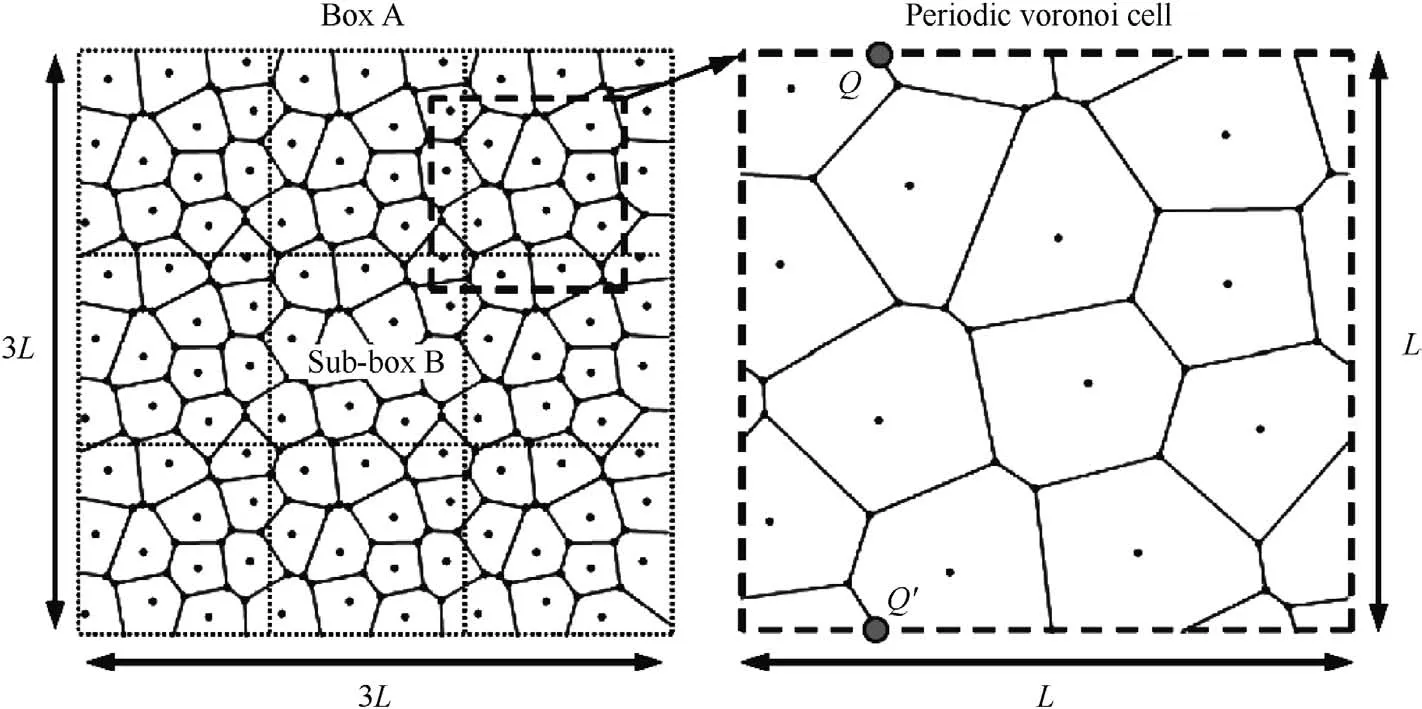
Fig.2.A periodic Voronoi cell derived by controlling the points.

PBX is a composite material consisted of crystalline particles and binders.The binders could be polymer materials as Estane and BDNPA-F,and the particles could be HMX or TATB[7].A representative volume element of PBX in the size of 500μm×500μm is constructed based on Voronoi cell,as shown in Fig.3.Every polygon represents a crystalline particle,and the area between them represents polymer binder.The depth of binder could be adjusted to control the content of binder.The depth of binder in RVE constructed here is 5μm,and the relevant volume fractions of binder and particle are 9.4%and 90.6%,respectively.

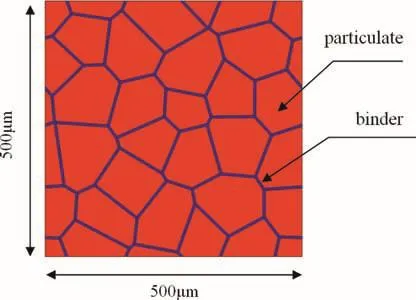
Fig.3.A representative volume element of PBX base on Voronoi cell.

No damage exists in RVE in Fig.3,each particle is completed and fully surrounded with binder.Actually,the initial damages exist in PBX,which result from press procedure before it is in charge.There are some kinds of damages in PBX as intragranular and interfacial cracks.Based on RVE in Fig.3,two representative volume elements with interfacial and intragranular cracks shown in Fig.4 are established,respectively,to simulate the effects of initial damages.Since the RVE is periodic,all the cracks in it are also periodic.

In this paper,the fracture behavior of PBX under quasistatic tension is simulated by finite element method.All the simulations are implemented in ABAQUS software.The mesh grids and loading boundary are shown in Fig.5(b).There are about 10,000 plane strain elements,most of which are quadrilateral elements,and the rest are triangular elements in transitional regions.Different treatment methods are utilized to the initial damages in the model.If there is no damage in the model,the grids of particle and binder are tied together.If there is interfacial crack between particles,the grids between them are removed.If there are intragranular crack inside a particle,the contact elements are employed.When the tensile fracture process of PBX is simulated,the loading condition must be derived from the experiment.Palmer[13]performed a Brazil test of PBX 9501 using curved anvils,and the test geometry is shown in Fig.5(a).In Palmer's experiment,the strain rate is about 10-4s-1,and the tensile failure stress of PBX 9501 is 0.78±0.1 MPa.The loading condition is determined by the centre zone in disc which has dimension of 500μm×500μm.It is not easy to measure the stress state on boundary of the centre zone.However,according to Awaji's[14]and Huang Fenglei's[4]works,the boundary stressshould be applied to the boundaries in different directions,and the boundary stressescan be calculated by the tensile failure stress and some parameters from the test geometry.Herein,the uniformly distributed stress is applied to the boundaries of the model,and the evolution of applied stress condition with time is derived,as shown in Fig.6.The boundary stressesare 1.516 MPa and-4.682 MPa,separately,at the time 100 s,so that the strain rate of simulation is the same as that of the Brazil test.

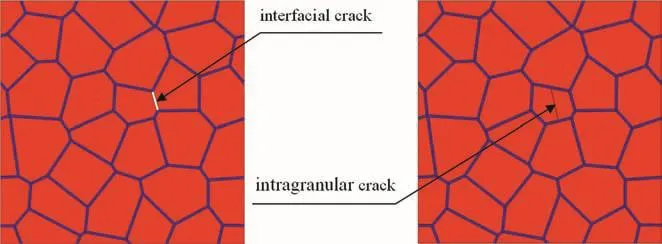
Fig.4.RVEs with two kinds of initial damages.

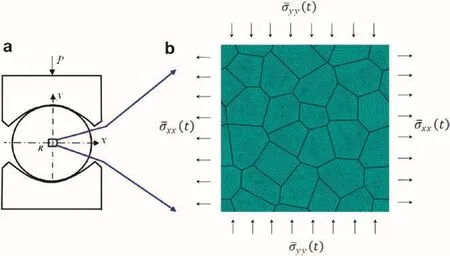
Fig.5.Brazil test geometry[13]and loading condition on the meshes grids.

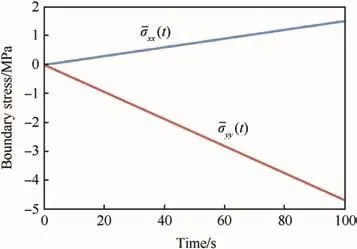
Fig.6.Evolution of boundary stresses as function of time.

2.2.Constitutive models for components

According to large amount of experiments,the main form of damage in PBX under tensile loading is interfacial crack.The microscopic crack path of PBX 9501 under tensile loading is shown in Fig.7.A main crack path exists obviously,and it mainly propagates along the edges of lager particles[8].

Fig.7.The microscopic crack path of PBX 9501 under tensile loading[8].

The fracture behavior of PBX under tension is significantly influenced by the interfacial property between crystals,but the interfacial property is complex to exhibit.Most research assumed that the relation between traction and opening displacement(cohesive law)was linear in the past[9,10].Tan[11]used the digital image correlation(DIC)method to obtain an inelastic cohesive law,and proposed an analytic expression.This expression has three parameters,such as adhesive strength σmax,elastic modulus kσand soften modulus~kσ.

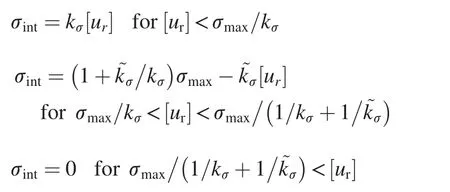
where σintis interface normal stress;and[ur]is opening displacement.As shown in Fig.8,this relation is composed of three elastic stages.

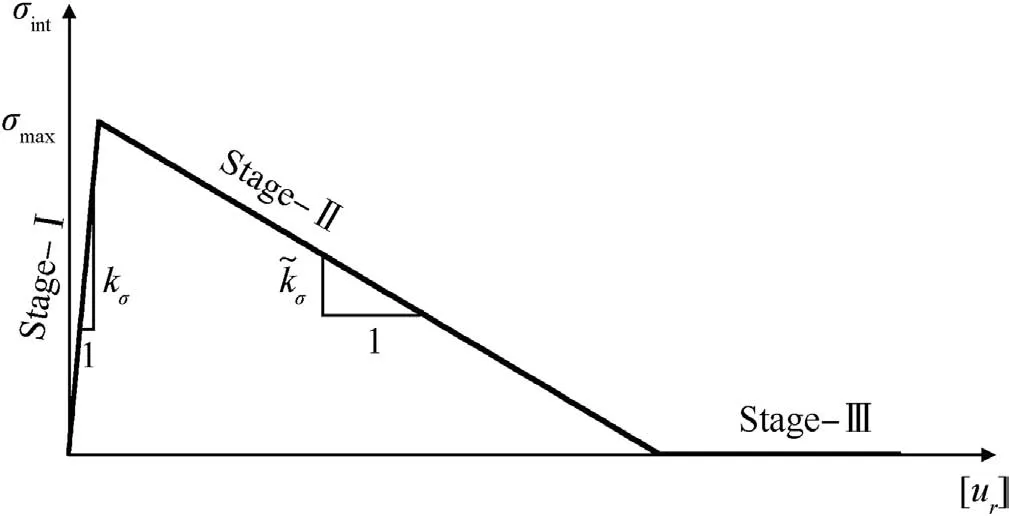
Fig.8.The relation between normal stress and opening displacement of interface[11].

The depth of binder is ignored in the expression above.In this paper,we consider the depth δ of binder into cohesive law,and substitute the interface normal strain εintfor opening displacement[ur].The relation between εintand[ur]is

Furthermore,the relation between tangential strain and tangential displacement is considered the same as the normal relation.The values of adhesive strength,elastic modulus and soften modulus are 1 MPa,1.55 GPa/μm and 15 MPa/mm,respectively,referring to Ref.[12].The Poisson ratio of binder is 0.49.The crystalline particle is assumed to be linear elastic during numerical simulation.The modulus and Poisson ratio of particles are 30 GPa and 0.322,respectively.

3.Results and discussions

3.1.Effect of interfacial debonding

The fracture process of the model with no initial damage under quasi-static tension is simulated by finite element method.The comparison between simulated tensile stress--strain relation and experimental data is shown in Fig.9.Our simulated result is in agreement with the experiment data which is from a Brazil experiment of PBX9501 in Ref.[13].There is a smooth and relatively long stage of strain-hardening in both curves in Fig.9,while some fluctuations turn out around stress peak in simulated curve.Fig.10 shows the details of the fluctuations,where strain softening and hardening alternatively appear.

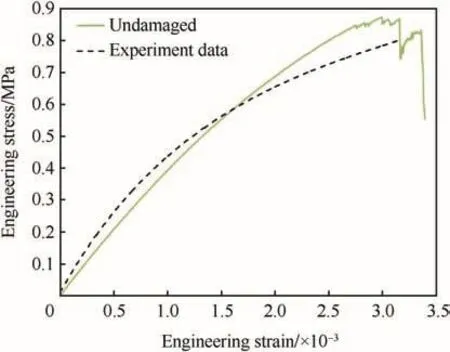
Fig.9.Tensile stress and strain relation of model with no initial damage and experimental data(experiment is from Palmer et al.,1993[13]).

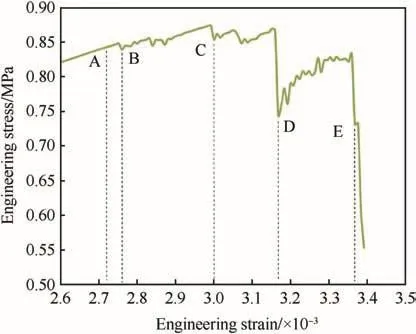
Fig.10.Details around stress peak from Fig.8.

Moreover,Fig.11 shows the fracture process at six typical time points which are A,B,C,D,E and F in loading sequence.The first five time points in Fig.11 correspond to the time points in Fig.10.Because of the different mechanical properties,the stress level in the regions between crystals is higher than that in other regions significantly when a tensile load is applied,as shown in Fig.11A.A phenomenon of interfacial debonding exists with the increase in loading.A meso-crack appears at time point B,and four cracks appear at time point C.It seems that the interface debonding tends to occur in the interface perpendicular to the loading direction,and the interface debonding leads to the nucleation and propagation of meso-cracks.New cracks nucleate when the cracks propagate at time points D and E.Finally,a main crack is generated at time point F.The model is completely separated into several parts.The main crack path is an irregular line and approximately perpendicular to the loading direction.

The interfacial debonding is also a main reason of the fl uctuations around stress peak,as shown in Figs.10 and 11.Before time point A,the stress raises with the increase in strain.At time points B,a crack is generated,the stress decreases,and a kind of strain softening appears.After a minimal value of time,the stress increases again until another crack generates.At time points C and D,the similar phenomenon appears again,and the strain hardening and strain softening are more obvious than that at time point B because of more cracks.At time point E,almost two separate parts are generated,and a small amount of binder leaves between the two parts.Stress decreases more and increases less subsequently at time point E.At time point F,a main crack forms and the stress no longer increases.It seems that this phenomenon is related to fracture energy,which needs further investigation.

3.2.Effect of initial damage

The fracture processes of models with no damage,an interfacial crack and a transgranular crack initially under quasi-static tension are simulated to study the effects of initial damages on fracture behavior of PBX.The relation of tensile stresses and strains of the three models is shown in Fig.12.The experimental data is also from a Brazil experiment of PBX9501 in Ref.[13].Compared to the curve of model with no initial damage,the modulus,peak stress and peak strain of the models with initial damage are all smaller.Moreover,the peak stress and peak strain of the model with an interfacial crack is larger than that of the model with a transgranular crack.On the other side,the curves of the models with initial damages are more approximate to the experiment data than those of model with no initial damage because the samples utilized in experiment are with initial damages actually.

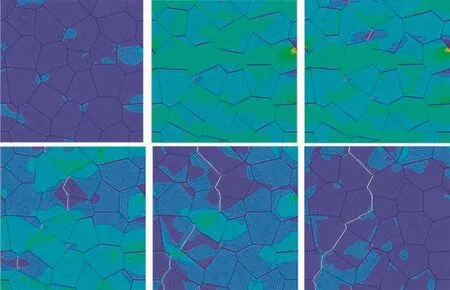
Fig.11.Fracture process of model with no initial damage under tension.

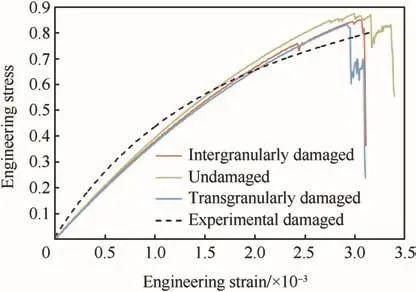
Fig.12.Tensile stress and strain relations of models with no initial damage and different initial damages(experimental results follow Palmer et al.,1993[13]).

The stress distribution and the fracture behavior are influenced by the initial damages in material.The stress concentration is found in some regions through numerical computation.The simulated results of three models before(above)and after(below)fracture are shown in Fig.13.It is found that the main crack path is significantly affected by the initial damages.The crack would propagate from the tips of initial cracks,resulting from the stress concentration there.Because of initial damages,the main crack paths are deviated from that of model with no initial damage.Actually,the initial damages in PBX after press process are with irregular shapes and different sizes which is more complex than the models used above.This is the reason why it is hard to predict the crack path of PBX.Definitely,the crack path is influenced by the size and direction of initial meso-cracks,which needs further investigation.

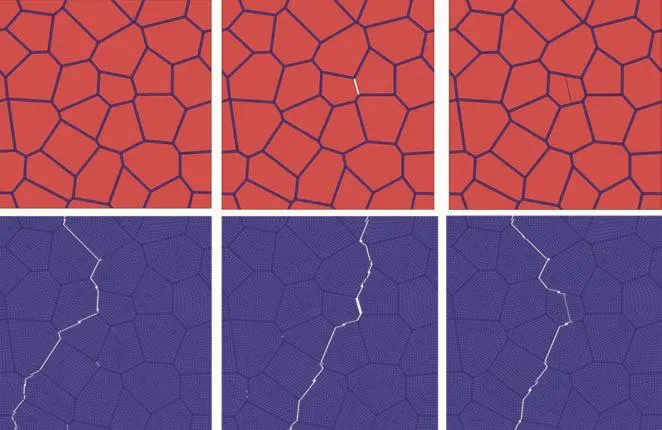
Fig.13.The models before(above)and after(below)fracture.

4.Conclusions

A two-dimensional representative volume element was constructed based on Voronoi model in which the component contents could be regulated and the particles are randomly distributed.A nonlinear damage model of polymer matrix was employed.The fracture behavior of PBX under quasi-static tension was simulated.The results showed that the simulated strain-stress curves is coincident with experimental data.It was found that strain softening and hardening alternatively appear around peak stress.

The interface debonding leads to the nucleation and propagation of meso-cracks,and the main crack is approximately perpendicular to the loading direction.The interface debonding tends to occur in the interface perpendicular to the loading direction.The initial damages of intragranular and interfacial cracks decrease the modulus and failure stress,and the main crack tends to propagate toward initial meso-cracks.The relation of stress fluctuation and fracture energy and the effects of the initial crack size and direction on fracture behavior need further investigation.

[1]Luo JR.Study on damage,fracture and constitutive relation of PBX.Mianyang:China Academy of Engineering Physics;2001.pp.1-17.

[2]Banerjee Biswajit,Adams Daniel O.Micromechanics-based determination of effective elastic properties of polymer bonded explosives.Physica B 2003;338(1-4):8-15.

[3]Li JL,Fu H.Fracture behavior investigation into a polymer-bonded explosive.Strain 2012;48(6):463-73.

[4]Wu YQ,Huang FL.A micromechanical model for predicting combined damaged of particles and interface debonding in PBX explosves.Mech Mater 2009;41(1):27-47.

[5]Pei-de Zhou.Computing geometry.Beijing:Tsinghua University Press;2008.

[6]Gan YX.Voronoi modeling of the constitutive behaviors of cellular solids.Xi'an:Xi'an Jiaotong University;2005.

[7]Gray III GT,Idar DJ,Blumenthal WR,Cady CM,Paterson PD.Highand low-strain rate compression properties of several energetic material composites as a function of strain and temperature.In:Eleventh international detonation symposium,Colorado,August 31 through September 4,1998;1998.pp.76-84.

[8]Rae PJ,Goldrein HT,Palmer SJP,Field JE,Lewis AL.Quasi-static studies of the deformation and failure ofβ-HMX based polymer bonded explosives.Proc R Soc Lond A 2002;458(2019):743-62.

[9]Wu YL,Ling Z,Dong ZF.Stress-strain fields and the effectiveness shear properties for three-phase composites with imperfect interface.Int J Solids Struct 1999;37(9):1275-92.

[10]Zhong Z,Meguid SA.On the elastic field of a spherical inhomogeneity with an imperfectly bonded interface.J Elast 1997;46(2):91-113.

[11]Tan H,Liu C,Huang Y,Geubelle PH.The cohesive law for the particle/matrix interfaces in high explosives. J Mech Phys Solids 2005;53(8):1892-917.

[12]Tan H,Huang Y,Liu C,Geubelle PH.The Mori-Tanaka method for composite materials with nonlinear interface debonding.Int J Plast 2005;21(10):1890-918.

[13]Palmer SJP,Field JE,Huntley M.Deformation,strengths and strains to failure of polymer bonded explosives.Proc R Soc Lond A 1993;440(1909):399-419.

[14]Awaji H,Sennosuke S.Diametral compressive testing method.J Eng Mater Technol 1979;101(2):139-47.