基于RBF和POU的曲面重建方法

邓珍荣，彭希为，黄文明

（1.桂林电子科技大学计算机科学与工程学院，广西桂林541004；2.中国农业银行吉安分行，江西吉安343000）

0 引 言

曲面重建是逆向工程中最重要的关键技术，目前已经取得了不少研究成果。在诸多曲面重建方法中，隐式曲面重建方法引起了各国学者越来越多的关注。1982年，Franke率先使用径向基函数解决点云数据的插值问题。1999年，Turk提出了变分隐式曲面重建方法，该方法的时间复杂度和空间复杂度分别为O（N3）和O（N2）。此后，Carr使用贪婪算法对点云数据进行快速曲面重建，使得时间复杂度由O（N3）降为O（Nlog N），空间复杂度也由O（N2）降为O（N），实现了大规模点云数据的隐式曲面重建。但是，该方法使用的径向基函数仍然是全局支撑函数，并且需要为每个插值中心增加两个离面约束点。这使得该方法的效率受到一定程度的影响，导致该方法难以被广泛应用。除此之外，Morse、Ohtake、Tobor等人也分别提出了不同的基于径向基函数的曲面重建方法。随着该方法不断的改进，已从最初只能对几千个数据点进行曲面重建发展到现在可以实现大规模点云数据的多尺度曲面重建。无论是重建曲面的品质，还是重建效率都有了大幅度提高。

在文献［6－8］的方法基础上，本文提出了一种基于RBF和POU的曲面重建方法，根据点云模型的形状和分布密度，采用二叉树递归分解点云空间，能够有效控制点云空间的分解程度，确保重建曲面的连续性和光滑性。

1 理论基础

1.1 径向基函数插值理论

给定三维空间中的一个点集P＝｛pj∈R3｜j＝1，2，…，N｝，实数集H＝｛hj∈R｜j＝1，2，…，N｝是P对应的约束值。如果可以构造一个标量函数f:R3→R，使得

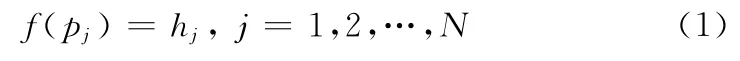
则由方程f（p）＝0可以定义一个隐式曲面。

对于方程f（p）＝0所描述的曲面，其光滑性可以通过能量函数E来衡量

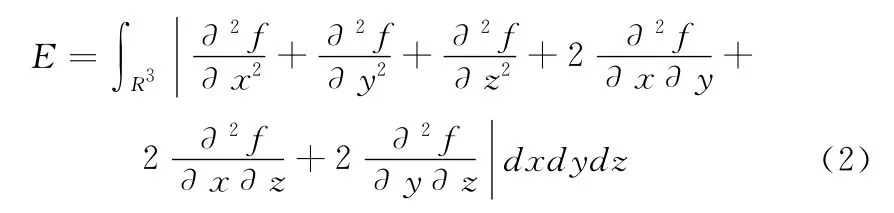
如果该曲面不存在曲率变化较大的区域，则能量函数E的值较小。文献［2］指出使用径向基函数建立的隐式曲面方程可以使能量函数E取得最小值，这就保证了隐式曲面的连续性和光滑性。其表达形式为

其中，p表示隐式曲面上的任意一点；pj表示用于定义隐式曲面方程的数据点，称为约束点或者插值中心；是径向基函数；为欧几里德范数；ωi是的权系数；R（p）是一个一阶多项式，用于确保隐式曲面的连续性。对于隐式曲面上的任意一点（x，y，z），R（p）的表达形式为R（p）＝r0＋r1x＋r2y＋r3z。

根据约束值的不同，用于定义隐式曲面方程的约束点可以分为两类。一类称为插值约束点，即点云中的数据点，它们位于隐式曲面上，对应的约束值为0；另一类称为离面约束点，必须额外获取，它们不位于隐式曲面上，对应的约束值不为0。文献［2］定义了3种不同类型的离面约束点，包括:内部约束点、外部约束点和法矢约束点。

为了求解权系数ωi和多项式R（p）的系数r0，r1，r2，r3，f（p）必须满足两类约束点给定的约束条件

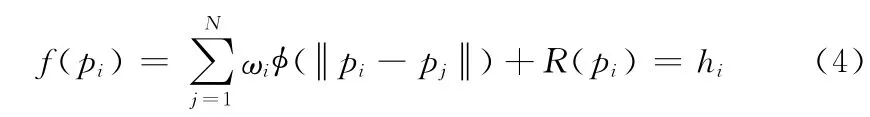
和正交条件

线性方程组的左边是一个半正定的矩阵，因而存在唯一的一组解（ω1，ω2，…，ωN，r1，r2，r3，r4）。将其代入式（3），即可得到隐式曲面方程。

1.2 单元分解原理

单元分解（partition of unity，POU）的主要思想是“分而治之”，即将全局问题分解成局部问题求解，然后对局部解加权求和得到全局解［8］。

给定三维空间中的一个点集P＝｛pj∈R3｜j＝1，2，…，N｝，Ω是P所在空间域。首先，将Ω分解成M个相互重叠的子域｛Ωi｜i＝1，2，…，M｝，并使得Ω∪Ωi；然后，分别对这些子域中的点集｛Pi｜PiP∩i＝1，2，…，M｝进行曲面重建，得到相应的局部重构函数｛fi（p）｜p∈Pi∩i＝1，2，…，M｝；最后，构造一组非负的紧支撑函数｛wi（p）｜∑wi＝1∩i＝1，2，…，M｝作为权重系数，对所有局部重构函数加权求和得到全局重构函数

约束条件∑wi＝1由加权函数｛Wi（p）｜i＝1，2，…，M｝经过正则化处理

加以满足；其中，加权函数Wi（p）必须保证全局重构函数F （P）的连续性，即在子域Ωi的边界处必须是连续的。

2 方法描述

2.1 点云空间自适应分解

运用单元分解原理进行曲面重建时，首先必须将点云空间分解成若干个相互重叠的子域。子域可以是任意形状，实际应用时通常选用包围盒形、球形和椭球形。由于局部重构函数的计算仅取决于子域中的数据点，因此子域中的点数将对曲面重建的品质和效率产生直接的影响。如果子域中的点数过多，则曲面重建的效率不高；如果子域中的点数过少，则重建曲面的精度难以保证。有鉴于此，本文采用二叉树递归分解点云空间，通过调节事先设置的四个参数来控制点云空间的分解程度。这4个参数分别为Tleaf、Tmin、Tmax和q。其中，Tleaf用于控制二叉树叶子结点中的点数；Tmin、Tmax和q用于设定重叠区域中的最少点数。

以下是二叉树及其结点的数据结构:

读取点云数据，查找点云中数据点在X、Y、Z轴上的最大坐标值和最小坐标值，进而构造一个棱边与坐标轴平行并且包含所有数据点的长方体包围盒作为二叉树的根结点。对根结点进行递归分解，使二叉树结点中的点数逐层减少，所有叶子结点中的点数介于Tleaf/2和Tleaf之间。如图1所示，Ωl是二叉树的某个结点。如果Ωl中的点数nl小于等于Tleaf，则将Ωl标记为“叶子结点”，不再对其进行分解；否则，将Ωl标记为“非叶子结点”，继续对其进行分解。具体步骤如下所述:

步骤1 确定Ωl的最长轴，用垂直于该轴的平面将Ωl分割成两个大小相同的子域C1、C2。其中，C2中的点数大于等于C1中的点数。由于nl＞Tleaf，因此C2中的点数大于Tleaf/2。

步骤2 扩大C1，使之与C2重叠。如果重叠区域中的点数大于等于Toverlap并且C1中的点数大于等于Tleaf/2，则执行下一步骤；否则，继续扩大C1，直到满足上述两个条件。其中

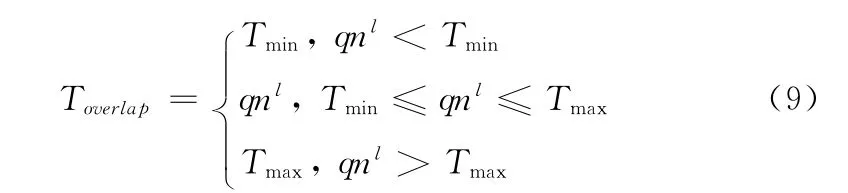
图1 二叉树结点的分解

以下是点云空间自适应分解的伪代码:

2.2 局部曲面重建

使用径向基函数建立各个子域的隐式曲面方程时，如果仅由插值约束点来定义隐式曲面，则线性方程组（6）会产生平凡解。因此，必须额外增加离面约束点以解决上述问题。

本文采用法矢约束方式［2］为子域中的每个插值约束点构造一个离面约束点。给定子域中的某一插值约束点pi，ni是点pi的法向量。将点pi沿其法矢方向偏移一段距离d即可得到与之对应的离面约束点pi′＝pi＋dni。如果点pi′位于点云模型的内部，则其约束值hi′＞0；如果点pi′位于点云模型的外部，则其约束值hi′＜0。对子域中的两类约束点进行插值即可得到局部重构函数fi（p）。

2.3 构造全局重构函数

对局部重构函数｛fi（p）｜i＝1，2，…，M｝加权求和得到全局重构函数F （P）。其表达形式为

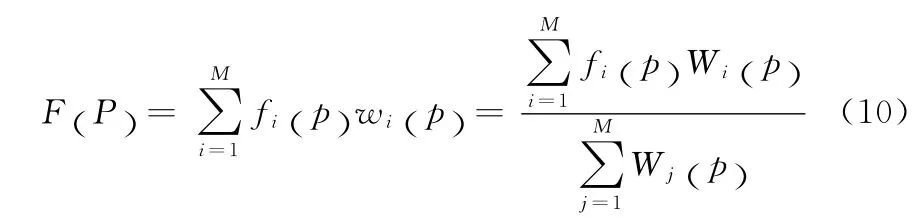
函数Wi（p）必须保证全局重构函数F （P）的连续性。本文采用文献［6］中的方法将函数Wi（p）定义为距离函数与衰减函数的组合Wi（p）＝V Di（p）；其中，距离函数Di（p）在子域Ωi边界处的值为1。对于棱边与坐标轴平行的包围盒形子域，选用距离函数

受V（0）＝1，V（1）＝0，V′（0）＝V′（1）＝0等条件的约束，衰减函数V可以从以下公式中选择

根据所选衰减函数V的不同，函数Wi（p）能够满足不同的连续性要求。

3 实验结果及分析

在配有Pentium IV 3.0 GHz和2GB内存的计算机上使用VC＋＋6.0和OpenGL实现了本文方法，然后使用Bloomenthal方法［9］对隐式曲面进行绘制。图2为bunny、igea、dragon和lucy的原始点云。图3为本文方法的曲面重建效果。

4 结束语

在现有研究成果的基础上，本文提出了一种基于RBF和POU的曲面重建方法。实验结果表明:该方法能够根据点云模型的形状和分布密度，自适应地分解点云空间，确保重建曲面的连续性和光滑性。

当然本文算法也有需要进一步改进的地方，比如，仅由插值约束点来定义隐式曲面会产生平凡解，是否有一个方法不需要额外增加离面约束点来解决上述问题，这是值得研究的。

图2 原始点云

图3 曲面重建效果

［1］Beatson R K，Levesley J，Mouat C T.Better bases for radial basis function interpolation problems［J］.Journal of Computational and Applied Mathematics，2011（4）:434－446.

［2］PAN Rongjiang，MENG Xiangxu，TaegKeun Whangbo.Hermite variational implicit surface reconstruction［J］.Science in China Series F:Information Sciences February，2009，52（2）:308－315.

［3］Arnaud Gelas，Sébastien Valette，Rémy Prost，et al.Variational implicit surface meshing［J］.Computers ＆Graphics，2009，33:312－320.

［4］Du Xinwei，Yang Xiaoying，Liang Xuezhang.Surface reconstruction of 3D scattered data with radial basis functions［J］.Communications in Mathematical Research，2010（2）:183－192.

［5］LIU Li，ZHAO Fengqun.ENO scheme based oil interpolation of radial basis function［J］.Computer Engineering and Applications，2013，49（2）:53－56.

［6］Yutaka Ohtake，Alexander Belyaev，Hans－Peter Seidel.Sparse surface reconstruction with adaptive partition of unity and radial basis functions［J］.Graphical Models，2006，68（1）:15－24.

［7］ZHAO Jiandong，KANG Baosheng，KANG Jianchao，et al.An improved surface reconstruction algorithm based on RBF［J］.Journal of Northwest University（Natural Science Edition），2012，42（5）:744－748.

［8］Lu Fangmei，Xi Juntong，Ma Dengzhe.Fast reconstruction of large scattered point clouds using adaptive partition of unity and radial basis functions［J］.Mechanical Science and Technology for Aerospace Engineering，2007，26（10）:1300－1303.

［9］Park Changsoo，Min Chohong，Kang Myungjoo.Surface reconstruction from scattered point data on octree［J］.Journal of the Korean Society for Industrial and Applied Mathematics，2012，16（1）:31－49.

［10］Zagorchev L G，Goshtasby A A.A curvature－adaptive implicit surface reconstruction for irregularly spaced points［J］.Visualization and Computer Graphics，2012，18（9）:1460－1473.