基于EEMD和HT的三相异步电机断相故障检测研究*

谢平波

（广东航道利用外资项目管理办公室，广东广州 510115）

0 引言

三相异步电机因诸多优点而成为目前应用最广泛的电动机[1]。但是在实际应用中它会发生各种故障，因此及时准确的故障检测显得尤为重要。断相故障是三相异步电机最常见的故障之一。恶劣天气、变压器、供电电路等多种因素都会引起断相故障的发生。三相异步电机带断相故障运行时，没有断相的定子绕组上的电流急剧增加，会产生大量热量，温度升高。如果长时间断相运行，对电动机危害很大，甚至会造成电动机烧毁[2]。

目前针对三相异步电机断相故障检测已经开展了一定的研究。文献[3]利用人工神经网络成功地检测出断相故障的发生，但是检测的电压电流信号还需要经过离散傅里叶变换(DFT)，中间过程复杂，并且只能判断故障的发生与否，无法获取故障发生的其他信息[3]。文献[4]采用快速傅里叶变换(FFT)分析定子电流检测三相异步电机的断相故障，但是不能得到断相故障相关的时间信息。现有检测方法只着重检测断相故障的发生与否，而没有得到更多的故障信息[4]。

为了克服现有方法的不足，获取更多的断相故障信息，并针对故障发生时暂态过程的非线性和不稳定性，本文利用具有高度自适应性，专门分析不稳定、非线性信号的集合经验模态分解 （EnsembleEmpiricalModeDecomposition，EEMD）方法分析三相异步电机的定子线电压以检测断相故障。

1 三相异步电机断相故障

所谓断相是指由于三相异步电机的三相电源线或绕组内部任意一相断开造成的一种电动机单相或两相运行的故障状态。断相运行实际上是电动机不对称运行的极端情况，分为起动前断相和运行中断相。

三相异步电机在正常运行中发生断相故障后，电磁转矩变化不大，一般能够继续运行，但是电动机运行状态发生了很大变化。本章以星形接法的三相异步电机为例分析电源线断相后的运行状态。星形接法三相异步电机a相电源线断相如图1所示。

星形接法三相异步电机正常运行时输入功率为P：

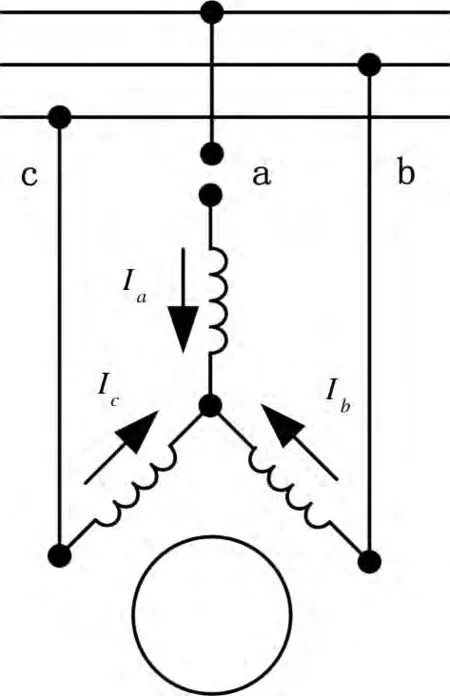
图1 星形接法三相异步电机a相电源线断相示意图

（1）式中：UL为定子线电压；IL为定子线电流； λ为功率因数。

a相电源线断开后，输入功率为：

（2）式中：I′L为断相运行时流过b、c两未断相定子绕组电流；λ′为断相运行时功率因数。

如果运行中负载功率不变，则断相运行与正常运行时的输入功率相同，即P′=P，则由（1）式和（2）式得出：

一般 λ′=0.9λ，则：

从以上分析可以得出，星形接法三相异步电机断相运行时，若负载功率不变，则没有断相的两相绕组电流将增至正常运行时候的2倍左右。实际上，三相异步电机不管是星形接法还是三角形接法，若断相故障发生后继续运行，都会导致绕组电流急剧增加。

断相故障开始结束时间的检测具有重要的意义。它不但对了解故障状态、分析故障原因、寻找故障位置等有重要的作用，定子绕组产生的热量更是与定子绕组流过电流的时间长短有关。

设定子单相绕组上所产生的热量为Q，电阻为R，流过该绕组的电流为I（t），断相故障开始时间为t1，结束时间为t2，断相故障持续时间t=t2-t1，则从t1到t2时刻在该绕组上所产生的热量为：

从上式可知，只要检测出断相故障开始和结束的时间，再结合该相定子绕组的电阻和电流就可以计算所产生的热量，以便有效防止电动机因温度过高而产生的安全问题。接下来详细阐述检测三相异步电机断相故障的集合经验模态分解和希尔伯特变换理论。

2 集合经验模态分解和希尔伯特变换

对检测信号进行集合经验模态分解之前，先要采取特定的方法对其进行降噪处理，以便提高信噪比，避免噪声对分析结果的有效性产生不利影响。

设含有噪声的一维信号为：

Xo（t） =X （t） +N （t）

Xo（t）为含噪声原始信号，X（t）为真实信号，N（t）为噪声。降噪处理的目的就是要降低噪声N（t）对真实信号X（t）的影响。本文利用小波包来降低信号噪声。小波包降噪方法由以下几个步骤组成：

（1）选取小波基、确定分解层次，进行小波包分解；

（2）给定熵标准，计算最优树，确定最优小波包基；

（3）确定每个小波包分解系数对应阈值并量化系数；

（4）利用小波包重构信号。

检测信号经过小波包降噪后，利用集合经验模态分解和希尔伯特变换对其进行分析处理。

2.1 集合经验模态分解（EEMD）

本文提出了一种基于集合经验模态分解的新型数据分析方法。它能够有效地解决经验模态分解(Empirical Mode Decomposition，EMD)中的模态混叠问题，得到的固有模态函数（Intrinsic Mode Function，IMF）更接近原始信号的真实性。该方法的步骤如下[5]：

观察组检出附件包块15例,原始血管搏动4例,盆腔积液10例,总共内假孕囊1例;对照组检出附件包块20例,原始血管搏动9例,盆腔积液15例,子宫内假孕囊16例;观察组显著优于对照组,P<0.05,差异有统计学意义,见表1。

（1）向经降噪处理得到的信号X（t）中加入白噪声S(t)得到：

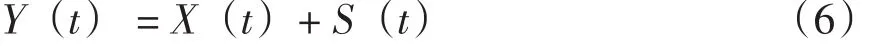
（2）对Y（t）进行经验模态分解（EMD）得到 IMF分量h1、h2、…、hj；

（3）重复以上步骤N次，其中第i次分解得到的 IMF分量为 hi，1、hi，2、…、hi，j；

（4）计算每次分解得到的IMF平均值。

则第j个IMF分量最终结果为：

每次经验模态分解前向信号X（t）中添加的白噪声Si（t）都是随机产生，相互独立。这是为了保证每一次分解不同，但每次加入噪声的幅值是相同的，由幅值系数k确定。

集合经验模态分解的误差记为e，则它与分解次数N、噪声的幅值系数k关系如下：

由式（8）可以得到，白噪声的幅值系数k越小，分解的误差越小。但是实践经验表明，当k小到一定程度时，就不能减小分解结果的误差。另外，一味增加分解次数N对分解结果的影响不大[6]。

2.2 希尔伯特变换（HT）

对给定信号x（t）做希尔伯特变换[8]得到：

解析信号 z（t） 由 x（t）、 y（t）组成，x（t）为实部， y（t）为虚部：

z(t)的幅值和相位分别是：

瞬时频率（Instantaneous Frequency，IF）为：

集合经验模态分解（EEMD）能够避免固有模态函数（IMF）之间的波形混叠问题，具有高度自适应性。它的基函数是在分解过程中依据信号的局部时间尺度得到的，所以不存在基函数选择问题[9]。希尔伯特变换得到的瞬时频率是局部性的，不受海森堡不确定性原理的影响[10]，在时域和频域内同时有更高的分辨率和精度。因此，集合模态经验分解在分析不稳定、非线性信号上面具有巨大的优势。

3 三相异步电机断相故障检测仿真

本文利用集合经验模态分解（EEMD）处理三相异步电机的定子线电压，对固有模态函数（IMF）做希尔伯特变换（HT）得到对应的瞬时频率（IF），在瞬时频率图上识别断相故障特征。三相异步电机断相故障检测原理图如图2所示：

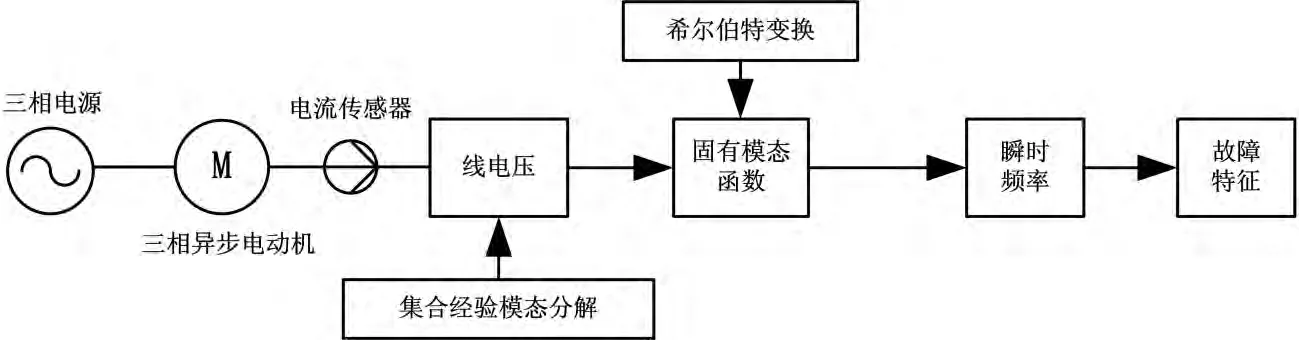
图2 三相异步电机断相故障检测原理图

为了获取三相异步电机断相故障检测信号，根据三相异步电机在两相静止坐标系下的数学模型在MATLAB/SIMULINK中搭建了仿真模型。将三相异步电机接入三相电压源，电压源a相连接断路器，断路器初始状态为闭合。设置断路器在0.5 s、1 s、1.5 s和2 s四个时刻动作，即发生了两次断相故障。第一次故障是从0.5 s开始，到1 s结束，持续时间0.5 s。第二次故障是从1.5 s开始到2 s结束，持续时间也是0.5 s。选取定子a、b两相之间线电压作为断相故障检测信号。

为了说明噪声对分析结果有效性的影响，先对未进行降噪处理的线电压检测信号进行分析，得到的IMF5瞬时频率如图3所示。

图3 未降噪的定子线电压Uab的IMF5瞬时频率图

从图3中得不到断相故障的有用信息，表明原始信号中的噪声严重影响了该方法的有效性，因此有必要对原始信号进行降噪处理。

经过小波包降噪处理的线电压Uab如图4所示：

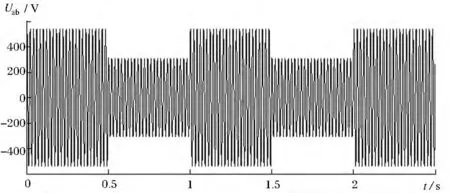
图4 降噪的定子线电压Uab

对其做集合经验模态分解（EEMD）得到14个IMF分量以及剩余分量。分解结果如图5所示。

如图5所示，从上到下依次为IMF1、IMF2、…、IMF14，最后一条曲线为剩余量。

图5 降噪的定子线电压EEMD分解结果

对IMF分量做希尔伯特变换得到对应的瞬时频率。IMF5的瞬时频率如图6所示。

图6 降噪的定子线电压IMF5瞬时频率图

图6 与未降噪的定子线电压IMF5瞬时频率图相比，具有明显的故障特征。在设置的故障开始和结束时刻瞬时频率幅值急剧变化，在其他时刻平稳波动，最终形成尖峰形状，并且故障开始时刻尖峰方向为正向，故障结束时刻尖峰方向为负向，故障期间瞬时频率比正常运行时波动幅度要大。

表1 第一次断相故障仿真设置时间和IMF5瞬时频率尖峰时间对照表

仿真设置时间和IMF5瞬时频率尖峰时间对照表如表1和表2所示。

据表分析，尖峰对应时间与所设置的故障开始结束时间极其吻合。

因此，在经过降噪处理的定子线电压IMF5瞬时频率图上，不仅可以根据尖峰标识判断出故障的发生和消除，还可以得到故障开始和结束的精确时间。

利用集合经验模态分解(EEMD)和希尔伯特变换(HT)处理断相故障的定子线电压，分析结果表明IMF5瞬时频率尖峰标识的断相故障特征非常准确、易于判断，并且还可以获得断相故障开始和结束时间的重要信息。

表2 第二次断相故障仿真设置时间和IMF5瞬时频率尖峰时间对照表

4 结论

本文提出了一种基于集合经验模态分解（EEMD）和希尔伯特变换（HT）的新型信号分析方法，并成功运用于检测三相异步电机的断相故障。仿真实验结果表明采用该方法不仅能够准确地检测出断相故障的发生与消除，并且还能够获取断相故障精确的开始和结束时间，据此可以计算出断相故障的持续时间。

［1］唐介.电机与拖动：第2版［M］.北京：高等教育出版社，2007.

［2］Abid Javed，Tahir Izhar.An improved method for the detection of phase failure faults in poly phase induction machines［C］.Third international conference on electrical engineering，Lahore：ICEE，2009.

［3］Sri Kolla，Logan Varatharasa.Identifying three-phase induction motor faults using artificial neural networks［J］.ISA Transactions，2000，39（4）：433-438.

［4］ M.E.H.Benbouzid，H.Nejjari，R.Beguenane，et al.Induction motor asynchronous faults detection using advanced signal processing techniques［J］ .IEEE Transactions on Energy Conversion，1999，14（12）：150.

［5］Shufeng Ai，Hui Li.Gear fault detection based on ensemble empirical mode decomposition and Hilbert-Huang transform ［A］.Fifth international conference on fuzzy systems and knowledge discovery ［C］.Shandong：FSKD，2008.

［6］窦东阳，赵英凯.集合经验模式分解在旋转机械故障诊断中的应用［J］.农业工程学报，2010，26（1）：191-192.

［7］ Hui Li，Yucai Wang，Yanfang Ma.Ensemble empirical mode decomposition and Hilbert-Huang transform applied to bearing fault diagnosis［A］.Third international congress on image and signal processing［C］，Yantai：CISP，2010.

［8］ Antonio Garcia Espinosa，Javier A.Rosero，Jordi Cusido，et al.Fault detection by means of Hilbert-Huang transform of the stator current in a PMSG with demagnetization ［J］.IEEE transaction on energy conversion，2010，25（2）：314.

［9］李天云，程思勇，杨梅.基于希尔伯特-黄的电力系统谐波分析［J］.中国电机工程学报，2008，28（4）：109-110.

［10］ Wang Zhan，Zeng Xiangjun，Hu Xiaoxi，et al.The Multi-disturbance Complex Power Quality Signal HHT Detection Technique［A］.Innovative Smart Technologies Asia［C］，Tianjin：ISGT，2012.