Temperature Distribution and Scuffing of Tapered Roller Bearing

WANG Ailin and WANG Jiugen*

Department of Mechanical Engineering,Zhejiang University,Hangzhou 310027,China

1 Introduction*

The rapid developments of high-speed roller bearings demand higher requirements for structural design,material selection,lubrication method and theoretical analysis of rolling bearings.Especially in the field of aerospace,high speed trains and automobile,and so on,tribological design problems deserve more and more attention such as fatigue life,thermal instability and scuffing failure of bearings.Tapered roller bearings have several advantages,such as compact structure,small radial size,high load capacity,small friction torque and lower operating temperature,thus tapered roller bearings are widely used in high-speed spindle assembly.The research into temperature distribution and scuffing possibility of tapered roller bearings has great significance in engineering practice.

Both experiments and theories pay extensive attention to heat transfer inside the bearings and scuffing failure of bearing elements.For experimental studies,ZANTOPULOS[1]made a series tests that tapered roller bearings were running under severe operating conditions,and used optical microscope,scanning electron microscope and metallographic examinations,proposed a qualitative model for the onset of scuffing.TARAWNEH,et al[2],used heaters embedded in two rollers to study the dynamics of heating in railroad tapered-rollers bearings,after the heat transfer inside the bearing,the temperature of outer raceway was measured with infrared sensing temperature method,and the experimental results were compared to zero-and first-order thermal models to estimate overall heat transfer coefficients of the bearings.In situ Raman spectroscopy was employed for real time correlation of contact surface chemistry to friction coefficient for solid lubricated contact[3],and this method was also used to acquire point spectra in a running EHL contact,and measure pressure,lubricant film thickness and temperature[4].

Theoretical analyses can be divided into two categories,one is to consider heat transfer in the whole surface of relative moving object,another concern is the actual contact area in terms of rough spots or hot spots.LING,et al[5],proposed a solution method for normal displacement of half-space under an arbitrarily distributed fast moving heat source.FLOQUET,et al[6–7],used the Fourier transform methods developed by Ling to analyze surface temperature,and their three dimensional analysis was verified with infra-red technique.GECIM,et al[8],selected a cylinder moving heat source,and used integral transform method to solve the heat conduction equation with cylindrical coordinate system.KENNEDY[9]analyzed the hot spots on the surface of relative moving object,and pointed out that the decrease of contact temperatures can be achieved with materials with higher thermal conductivity and higher heat capacity or with mechanical properties that have small stiffness,low yield stress or small coefficient of thermal expansion,which yields larger size hot spots.GECIM,et al[10],established transient temperature model in the vicinity of an asperity contact,they argued that the asperity achieves high transient temperature rise in a very short period of time,which may become the initial point of scuffing failure.In addition,there are several articles on the interactions of multiple heat sources problem[11–12].

Scuffing is a typical failure mode of tribological pairs in mixed lubrication under heavy load and high sliding speed.The theoretical models of scuffing for metals in contact were classified in terms of temperature,frictional power intensity,thermal instability,collapse of partial-ehl film,tribo-chemistry and plastic flow of surface layer[13].Furthermore,the factors of surface hardness,surface texture and roughness,load and sliding speed,temperature,lubricants and additives,and debris have effects on scuffing mechanisms and occurrence process of scuffing[14].WINER,et al[15],studied the thermal resistance of a tapered roller bearing,presented a thermal resistance model and verified their results with an infrared scanner and thermocouples.BRYANT[16]solved the heat conduction equation with the concept of a moving temperature wave and a novel form of an exponential Fourier transform.JANG,et al[17],developed a theoretical model to take into account of the speed variation with time,and illustrated the time-seizure characteristics.They investigated the effects of thermomechanical properties,operating speed,and convective heat transfer coefficient on seizure time of a journal bearing[18].ZHAI,et al[19],and BHUSHAN,et al[20],studied the thermal behavior and friction coefficient at surface asperity scale.ZHAI,et al[19],analyzed the viscous shearing and cooling of transportation of heat out of the thermally intensive asperity contacts,and side-flow of heat is weak in mixed lubrication.BHUSHAN,et al[20],studied the scale effects of hardness,mean contact size,asperity slope,number of contacts,summit radius of asperities on friction coefficient and temperature.In 1989,DUFRANE,et al[21],studied seizure of journal bearings with respect to thermal expansion of shaft and bearing bore.KHONSARI,et al[22],studied the transient thermoelastic behavior of shaft of journal bearing,and predicted seizure with the rule that operating clearance is removed as seizure appears.The scuffing failure of high speed rolling bearings under heavy load still is not well understood and the prediction of scuffing in those cases has practical meaning for high speed train and other rotating machines.

The objective of this study is to analyze temperature distribution and scuffing possibility of tapered roller bearings on the basis of internal contact stress[23].Cylinder moving heat source model proposed by GECIM,et al[8],and a slice method are utilized to calculate the internal temperature distribution and maximum temperature rise of bearing elements,and predict possible positions of scuffing.With the method and results of this study,the scuffing resistant design can be achieved for tapered roller bearings.

2 Temperature Calculation Model

The tapered rollers roll and slide on the inner raceway and outer raceway inside the bearing.The heat source model proposed by GECIM,et al[8],is used in present numerical modeling.Furthermore,the tapered roller bearing is divided into ten sections in the generation line of the tapered roller direction.Each slice can be approximated with a cylinder.The temperature distributions of tapered roller and raceways in each section are calculated respectively.

2.1 Heat conduction equation

Fig.1 shows the geometry and boundary of the slice model.The heat conductions in axial and circumferential directions are neglected,and the circumferential heat convection is taken into account.The heat flux distribution is uniform over the heating zone,φ0.Because the Hertzian contact width is very small,compared with the circumferential length of the tapered rollers,this assumption is reasonable.With the above assumptions,the equation of heat conduction is

where T is the difference between the actual temperature and the ambient(℃),r and φ are the cylindrical coordinates,ω is angular speed of tapered roller(rad/s),and α is thermal diffusivity(m2/s).

Defining the following variables:

where u is dimensionless temperature,h is convective heat transfer coefficient(W/(m2•K)),q is heat flux(W/m2),R is radius of the slices(m),k is thermal conductivity(W/(m•K)),and N stands for Peclet number.

Eq.(1)becomes

The boundary conditions at ρ=1 are

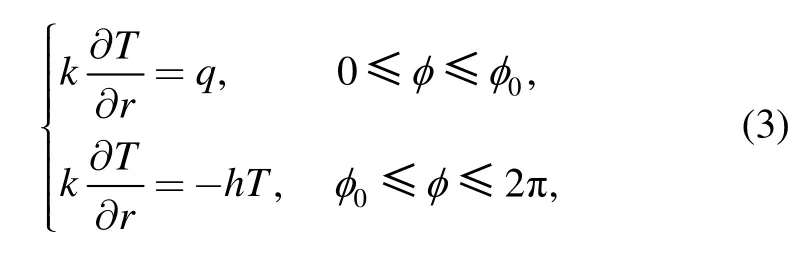
and u(ρ=0)is a finite value.

Using the finite Fourier transform,Bessel functions and Kelvin functions,Dimensionless temperature can be obtained:

For the process of the solution in detail can refer to Ref.[8].The maximum surface temperature with uniform heat input is at Φ=Φ0.Hence,Eq.(5)can be written as

where S represents the infinite summation.Defining

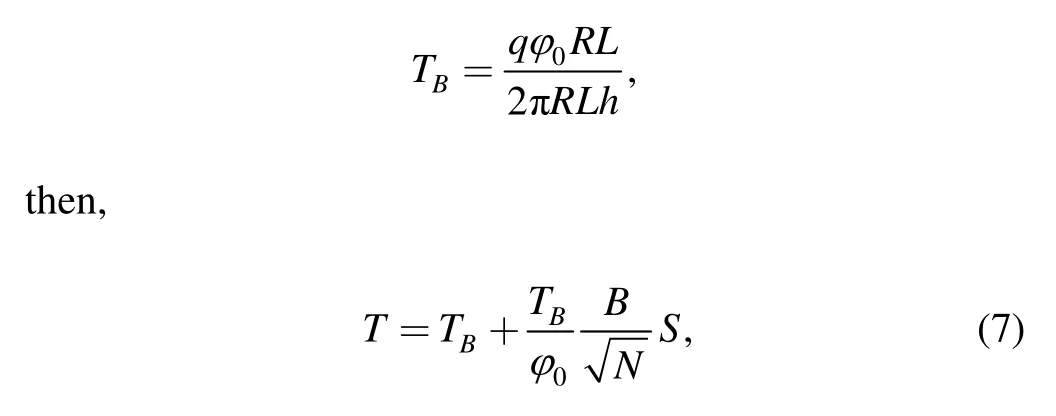
where TBis the bulk temperature andat φ=φ0and ρ=1.Eq.(7)can be rewritten as

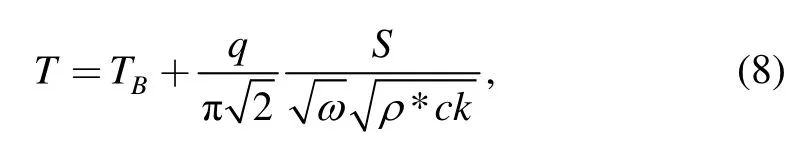
2.2 Friction power and heat distribution in interface

The power loss of bearing caused by friction can be calculated according to the following equation[24]:

where H is the power loss(W),and M stands for the frictional torque(N•mm).Assuming that frictional power Higenerated between roller and inner raceway is equal to friction power Hogenerated between roller and outer raceway,then

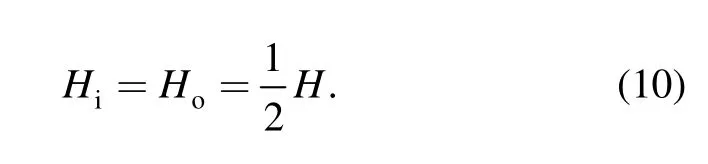
Heat partition at the interfaces complies with the following principles.

(1)Roller and inner raceway

The tapered roller contacts with the inner raceway under the normal load P,roller speed is u1,and the speed of inner raceway is u2,heat generated in the contact area is Q.Under rolling and sliding condition,the ratio of heat into the roller,Q1,and heat into the inner raceway,Q2,isas follows[25]:

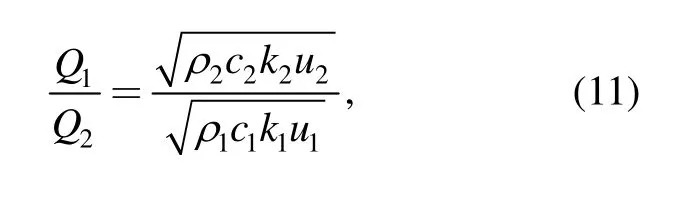
where ρ1and ρ2are densities of roller and inner raceway respectively(kg/m3),c is specific heat(J/(kg•K)),k is thermal conductivity(W/(m•K)),u is linear velocity of contact area(m/s),subscripts 1 and 2 represent roller and inner raceway respectively.

(2)Roller and outer raceway

The tapered roller is in contact with the outer raceway under the normal load P,and the roller speed is1u,heat generated in the contact zone is Q.Under pure sliding condition,the contact surface of outer raceway will continue to receive a portion heat λQ,and other(1-λ)Q will flow into tapered roller.The value of λ depends on the heat transfer characteristics of contact bodies.It can be assumed λ only depends on thermal diffusivities of tapered roller and outer raceway[26],written as

where α1=k1(ρ1c1),α3=k3(ρ3c3),α1und α3are thermal diffusivities of roller and outer raceway respectively(m2/s),ρ3is the density of outer raceway(kg/m3),subscript 3 represents outer raceway.

3 Scuffing Failure

3.1 Scuffing assessing criterion

WATKINS[27]proposed to evaluate seizure load with corresponding Hertzian contact dimension.If the wear scar is larger than the Hertzian contact width,mild scuffing occurs at the contact zone.The influence of original radial clearance is ignored in our calculation.Firstly,the thermal expansion of tapered rollers,inner raceways and outer raceways are calculated,and then the elastic approach of tapered roller-inner raceway contact pair and tapered roller-outer raceway contact pair are numerically analyzed.Finally,with the ratio of radial clearance to elastic approach,the scuffing possibility in the contact area is examined.

δHstands for the elastic approach of taperedroller bearing under load,and after thermal expansion roller radial increment is u1,radial increment of raceway is u2.When

the scuffing will occur in contact area of tapered roller and inner raceway,if Eq.(13)is satisfied.Otherwise,tapered roller and raceway contact area is safe in terms of adhesion wear.In Eq.(13),amount of thermal expansion of inner raceway is positive,and that of outer raceway is negative because it is a hole in geometry.

3.2 Thermal expansion

Recently,Assuming that inner raceway is free to expand,thermal deformation can be calculated by the next equation proposed by TIMOSHENKO,et al[28]:

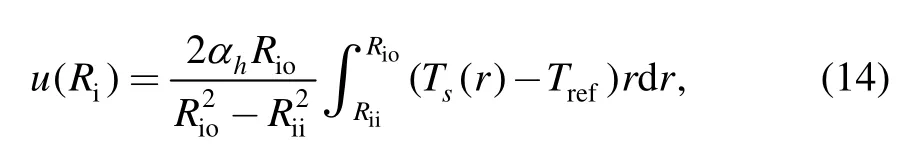
where αhis thermal expansivity of inner raceway,Riois outer radius of inner raceway,Riiis inner radius of inner raceway,Ts(r)is cross-sectional temperature,Trefis reference temperature.

With the above method,thermal distortion of outer raceway can be calculated by the next Eq.(15):

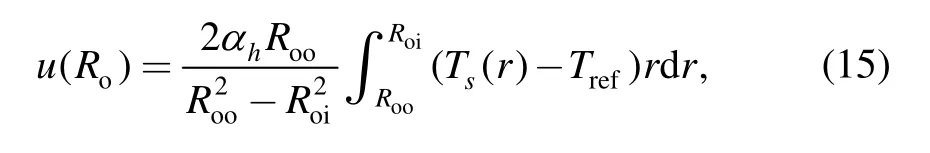
whereRoois outer radius of outer raceway,Roiis inner radius of outer raceway.

4 Results and Discussions

The widely used tapered roller bearing 30308 is selected as the object for numerical simulation,and its parameters are shown in Table 1 and Table 2.Many rolling bearings are manufactured with bearing steel GCr15,the rapid developments of high-temperature and high-speed bearings demand the usage of ceramic materials that have the low density,high strength,high hardness,good toughness,and the advantage of small thermal expansion coefficient,compared with rolling bearing steel.The distributions of contact stress,temperature and scuffing possibility are analyzed,when tapered rollers are produced with GCr15 or Si3N4are in contacted with inner ring and outer ring manufactured with GCr15.

Table 1.Parameters of tapered roller bearing

Table 2.Thermal parameters and elastic property

The surface heat convection coefficient is closely related to factors such as bearings surface size and shape,fluid viscosity and density,thermal conductivity and speed in heat transfer process,thus it is difficult to generally describe surface heat convection coefficient.An approximation calculating equation of convection coefficient is proposed in Ref.[24].If higher precision data of surface heat convection coefficient is needed,it can only be obtained with experiments.The convection coefficient is 600 W•m–2•K–1in this analysis,it is chosen based on mixed lubrication condition and lubricated with greases.

4.1 Contact stress distribution

As shown in Fig.2,under normal load 300 N,contact stress between the GCr15 tapered roller at its small end,middle point,and big end with inner races of GCr15 are 515.1 MPa,402.5 MPa and 489.4 MPa,respectively.The edge stress concentration between tapered roller and inner race occurs at tapered roller ends,and stress concentration is more serious at small roller end than that at big roller end.As shown in Fig.3,under normal load 300 N,contact stress between the Si3N4tapered roller and inner raceway of GCr15 at small end,middle point,and big end of tapered roller is respectively 561.8 MPa,440.1 MPa and 533.6 MPa.Compared to contact stress of GCr15 tapered roller with inner race,contact stresses of Si3N4tapered roller with inner race are higher,because the elasticity module of material Si3N4is larger than that of material GCr15,and the Poisson ratio of Si3N4is smaller than that of GCr15 bearing steel.

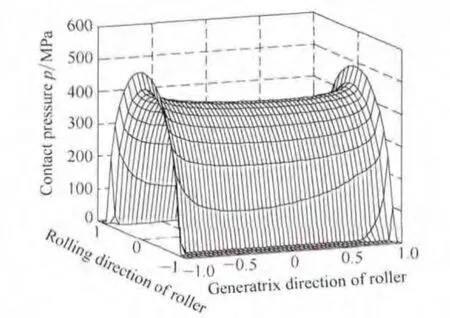
Fig.2.Contact stress between GCr15 tapered roller and GCr15 inner race under 300 N load

Fig.3.Contact stress between Si3N4tapered roller and GCr15 inner race under 300 N load

4.2 Temperature distribution

The contact area between tapered roller and raceways are divided along the tapered roller axis into ten slices,the maximum contact stresses occur on both ends of the tapered roller,the smallest occurs at the central point of the contact area,thus if the temperature at the three sections,that i=1,7,10,from the small end to its big end,are calculated,the temperature range of the whole contact area can be obtained.

Fig.4 and Fig.5 show the temperature distributions between GCr15 tapered roller and inner raceway,under the load is 300 N,the rotation speed is 5600 r/min and the convection coefficient is 600 W•m–2•K–1.In this case,the average bulk temperatures of small end,middle point and big end of tapered roller are accordingly TB1=23.8 ℃,TB2=20.9 ℃ and TB3=22.8 ℃.Eq.(6)indicates that the highest surface temperature appears at φ=φ0.

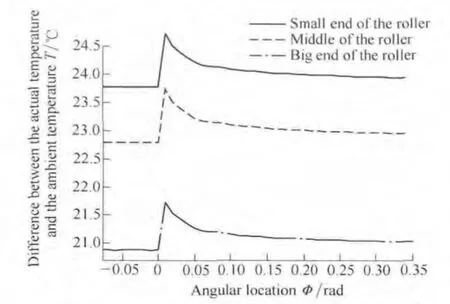
Fig.4.Temperature rise of GCr15 roller contacted with inner race

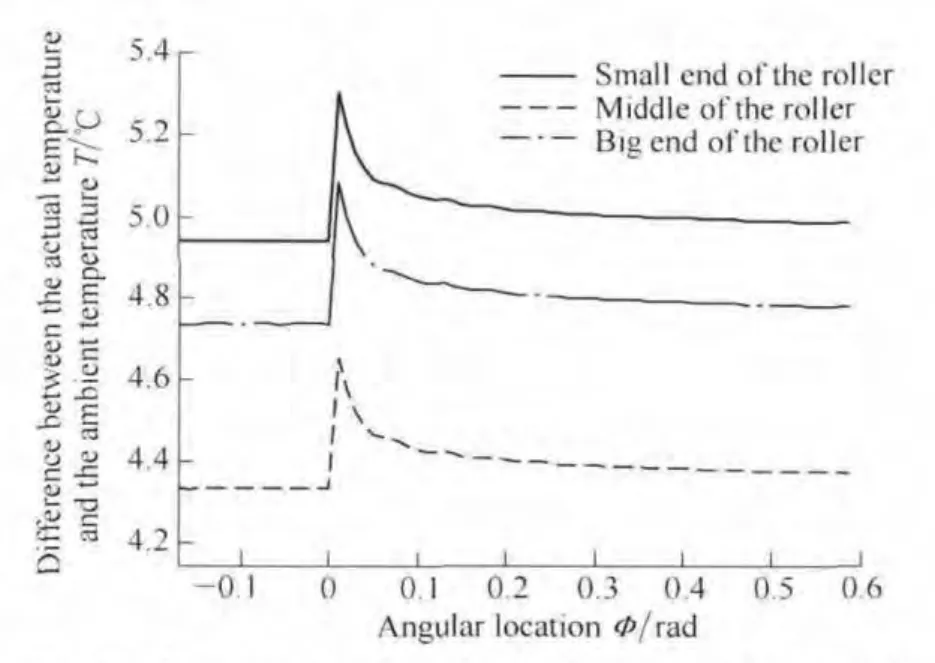
Fig.5.Temperature rise of GCr15 inner race contacted with GCr15 tapered roller

When the normal load,rotating speed and heat convection coefficient are changed,the temperature distributions at small end,middle point and big end of tapered roller are shown in Fig.6,Fig.7 and Fig.8.

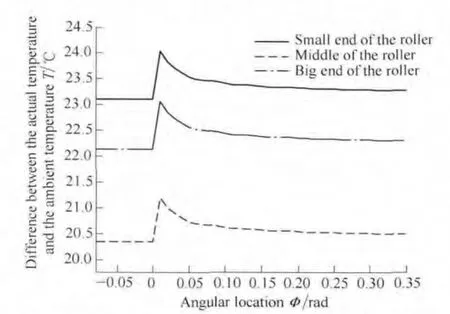
Fig.6.Temperature rise of GCr15 roller contacted with inner race when load is 200 N,rotation speed is 5600 r/min,convection coefficient is 600 W•m–2•K–1

Fig.7.Temperature rise of GCr15 roller contacted with inner race when load is 300 N,rotation speed is 2000 r/min,convection coefficient is 600 W•m–2•K–1

Fig.8.Temperature rise of GCr15 roller contacted with inner race when load is 300 N,rotation speed is 5600 r/min,convection coefficient is 1200 W•m–2•K–1

These figures indicate that when the heat is evenly distributed between the tapered roller and the inner raceway,small end of the tapered roller has biggest temperature rise,temperature at rollers’big end is secondly high,and the temperature rise of rollers’middle section is minimal.The normal load is associated with thermal power,when the load is low,the thermal power value is smaller,when the rotational speed reduces,thermal power value is also smaller.From the physical definition of heat convection coefficient h,it reflects the capability of heat transfer between fluid and solid surface.For higher heat convection coefficient h,more heat is taken away by lubricants,therefore the temperature rise of bearing components is much less.The above results can explain the changes of temperature rise of tapered rollers when normal load,rotational speed and convection coefficient change.

Fig.9 and Fig.10 show respectively the temperature rise of Si3N4tapered roller and inner raceway,when the normal load is 300 N,the rotation speed is 5600 r/min and heat convection is 600 W•m–2•K–1.The figures demonstrate,compared with the case of contacted with GCr15 inner raceway under same operation conditions,temperature rise of Si3N4tapered roller is higher than that of GCr15 tapered roller,and temperature rise of the inner race in contact with Si3N4tapered roller is lower than that of the inner race in contact with GCr15 tapered roller,because GCr15 tapered roller and GCr15 inner raceway receive equal heat flux,however,Si3N4tapered roller receives more heat flux than GCr15 inner raceway,according to the principle of heat distribution.

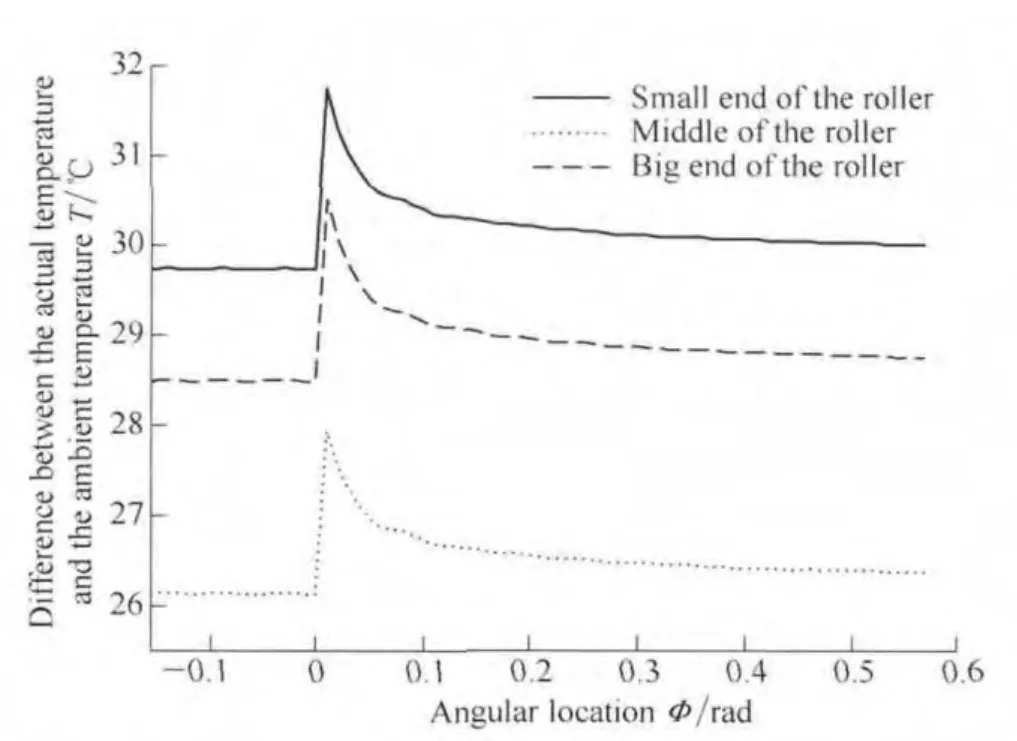
Fig.9.Temperature rise of Si3N4tapered roller contacted with inner race

Fig.10.Temperature rise of inner raceway contacted with Si3N4roller

4.3 Assessing of scuffing possibility

The elastic approach between GCr15 tapered roller and GCr15 inner raceway can be obtained with numerical method,which was described in detail in Ref.[12].If the biggest thermal expansion of GCr15 tapered roller is noted as u1i,and u2istands for the biggest thermal expansion of GCr15 inner raceway,the calculated results are listed in Table 3.

Table 3 demonstrates that when the normal load is 300 N,the rotation speed is 2000 r/min and the heat convection coefficient is 600 W•m–2•K–1,the big end of the tapered roller has the largest thermal expansion,and the small end of the inner ring has the highest thermal expansion.Scuffing failure appears at section 2,section 3,section 4,section 5,section 6 and section 7,however,the big end of the roller/inner raceway contact pair is safer than that of the small end of the tapered roller.

When the normal load is 300 N,the rotation speed is 2000 r/min and the heat convection coefficient is 600 W•m–2•K–1,the elastic approach δHobetween GCr15 tapered roller and GCr15 outer raceway,the biggest thermal expansion u1oof GCr15 tapered roller and the biggest thermal expansion u2oof GCr15 outer raceway are listed in Table 4.The biggest thermal expansion of the tapered roller occurs at its big end,and the biggest thermal expansion of the outer ring occurs at its small end.Scuffing does not appear between tapered roller and outer raceway in this case.

Table 5 shows the biggest expansions of Si3N4tapered roller and GCr15 inner raceway.Compared with the data in Table 3,the thermal expansion of Si3N4tapered roller is much smaller than that of GCr15 tapered roller,and the thermal expansion of GCr15 inner raceway contacted with Si3N4tapered roller is also smaller than that of GCr15 inner raceway in contact with GCr15 tapered roller,under same condition in terms of normal load,speed and convection coefficient,which explains the advantages of hybrid rolling bearings.The ceramic materials are used a lot in high temperature bearings.The biggest thermal expansion of the tapered roller occurs at its big end,and the biggest thermal expansion of the inner ring occurs at its small end.Scuffing failure does not appear between Si3N4tapered roller and GCr15 inner raceway.Furthermore,the big end of the tapered roller/inner raceway contact pair is safer than the contact pair of the small end of tapered roller/inner ring with respect to scuffing possibility.

Table 3.The biggest expansion and elastic deformation of GCr15 roller and GCr15 inner raceway μm

Table 4.The biggest expansion and elastic deformation of GCr15 roller and GCr15 outer raceway μm

5 Conclusions

The contact mechanics model,temperature model and scuffing failure model were synthesized to study the effects of normal load,speed,thermal conductivity and materials of tapered rollers on scuffing possibility.The scuffing possibility of tapered roller can be examined with our developed program.Based on the numerical results,several conclusions can be summarized.

(1)The increases of bearing load or rotational speed result in the increase of temperature of tapered roller surface and raceways.However,the increase of thermal conductivity leads to the decreases of temperatures of tapered roller and raceways.

(2)Compared with the bulk temperatures of tapered roller and raceways,their flash temperatures are smaller.

(3)When tapered roller of GCr15 or Si3N4are in contacted with inner ring of GCr15,the temperature of Si3N4roller is higher than that of GCr15 tapered roller,but the temperature of the inner ring contacted with Si3N4tapered roller is lower than the temperature of the inner ring in contact with GCr15 tapered roller.

(4)Under the same operation condition,the thermal expansion of Si3N4tapered roller is remarkably less than that of GCr15 rollers,this reveals the mechanism in which ceramic materials are widely used for high temperature rolling bearings.

(5)When the tapered roller contacts with the inner ring,the big end of the tapered roller has the biggest thermal expansion,and the small end of the inner ring also has the largest thermal expansion.At the tapered roller/outer ring interface,the biggest thermal expansion of the tapered roller occurs at its big end,and the biggest expansion of outer ring occurs at its small end.

(6)In the contact zone between tapered roller and the inner ring,complete scuffing,partial scuffing and no scuffing are all possible along the generator line,and the contact area of the big end of tapered roller is safer than that of its small end.At the tapered roller/outer ring interface,scuffing possibility is very smaller than that of the tapered roller/inner ring interface.

[1]ZANTOPULOS H.Some observations on scuffing in tapered roller bearings[J].Journal of Tribology,1998,120(3):427–435.

[2]TARAWNEH C M,COLE K D.Experiments and models for the thermal response of railroad tapered-roller bearings[J].International Journal of Heat and Mass Transfer,2008,51(25–26):5794–5803.

[3]MURATORE C,BULTMAN J E,AOUADI S M,et al.In situ Raman spectroscopy for examination of high temperature tribological processes[J].Wear,2011,270(3):140–145.

[4]HIMMEL D,MANSOT J L,BERCION Y,et al.In situ Raman microspectrometry of lubricated tribologic contacts.Part two:simultaneous measurements of pressure,lubricant film thickness and temperature distributions in a running EHD contact[J].Tribology Letters,2011,41(1):131–144.

[5]LING F F,MOW V C.Surface displacement of a convective elastic half-space under an arbitrarily distributed fast-moving heat source[J].Journal of Basic Engineering,1965,87(3):729–734.

[6]FLOQUET A,PLAY D,GODET M.Surface temperatures in distributed contacts-application to bearing design[J].Journal of Lubrication Technology,1977,99(2):277–283.

[7]FLOQUET A,PLAY D.Contact temperature in dry bearings-three dimensional theory and verification[J].Journal of Lubrication Technology,1981,103(2):243–251.

[8]GECIM B,WINER W O.Steady temperature in a rotating cylinder subject to surface heating and convective cooling[J].Journal of Tribology,1984,106(1):120–127.

[9]KENNEDY F E.Thermomechanical phenomena in high speed rubbing[J].Wear,1980,59(1):149–163.

[10]GECIM B,WINER W O.Tansient temperature in the vicinity of an asperity contact[J].Journal of Tribology,1985,107(3):333–342.

[11]GECIM B,WINER W O.Steady temperature in a rotating cylinder-some variations in the geometry and the thermal boundary conditions[J].Journal of Tribology,1986,108(3):446–453.

[12]YEVTUSHENKO A,TOLSTOJ-SIENKIEWICZ J.Temperature in a rotating ring subject to frictional heating from two stationary pins[J].Numerical Heat Transfer,Part A,2006,49(8):785–801.

[13]WANG Jiugen,YUAN Jing,XUE Zheng.Experimental investigation of scuffing failure with four-ball machine,part 2:theoretical models[J].Scientific Research Monthly,2007,35(11):40–43.

[14]WANG Jiugen,YUAN Jing,XUE Zheng.Experimental investigation of scuffing failure with four-ball machine,part 3:influence factors[J].Scientific Research Monthly,2007,35(11):44–47.

[15]WINER W O,BAIR S,GECIM B.Thermal resistance of a tapered roller bearing[J].ASLE Transactions,1986,29(4):539–547.

[16]BRYANT M D.Thermoelastic solutions for thermal distributions moving over half space surfaces and application to the moving heat source[J].Journal of Applied Mechanics,1988,55(1):87–92.

[17]JANG J Y,KHONSARI M M,PASCOVICI M D.Thermohydrodynamic seizure:experimental and theoretical analysis[J].Journal of Tribology,1998,120(1):8–15.

[18]JANG J Y,PASCOVICI M D.Modeling aspects of a rate-controlled seizure in an unloaded journal bearing[J].Tribology Transactions,1998,41(4):481–488.

[19]ZHAI X,CHANG L.Some insights into asperity temperatures in mixed film lubrication[J].Tribology International,2001,34(6):381–387.

[20]BHUSHAN B,NOSONOVSKY M.Scale effects in dry and wet friction,wear and interface temperature[J].Nanotechnology,2004,15(7):749–761.

[21]DUFRANE K F,KANNEL J W.Thermally induced seizures of journal bearings[J].Journal of Tribology,1989,111(2):288–292.

[22]KHONSARI M M,KIM H J.On thermally induced seizure in journal bearings[J].Journal of Tribology,1989,111(4):661–667.

[23]WANG Ailin,WANG Qingjiu,WANG Jiugen.Contact of tapered roller with logarithmic profile[J].Mechanical Science and Technology For Aerospace Enginnering,2012,31(5):836–841.

[24]HARRIS T A.Rolling bearing analysis[M].New York:John Wiley&Sons,Inc.,2001.

[25]WANG Jiugen,TAN Jianrong.Numerical simulation of traction in rolling/sliding contact[J].Journal of Tribology,1997,119(4):869–874.

[26]HALLING J.Principles of tribology[M].London:The Macmillan Press,1975.

[27]WATKINS R C.The use of the Hertzian dimension in wear scar analyses(application to four ball results)[J].Wear,1983,91(3):349–354.

[28]TIMOSHENKO S P,GOODIER J N.Theory of elasticity[M].Beijing:Tsinghua University Press,2004.