VPC优化格拉斯曼流形的视频人脸识别

吴育锋，徐向艺

(1.丽水学院工学院，浙江丽水323000;2.平顶山学院软件学院，河南平顶山467002)

视频人脸自动识别已广泛应用于许多新兴领域，如情感计算和智能人机交互(Human Computer Interaction，HCI)等［1］。由于二维相机的普及，大多数现有的人脸识别是使用2D静态图像或视频完成的［2］。然而，2D面部数据存在一些固有的问题，如光照条件变化和姿态变化等，三维数据形态可以有效地解决2D数据面临的问题［3］。文献［4］和文献［5］针对近期3D 人脸识别(Facial Expression Recognition，FER)给出了全面的研究，研究结果表明，如今几乎所有的3D人脸识别工作是基于静态3D图像的，通常认为3D视频可以就人脸的动态特征提供更多的信息，这对于人脸识别至关重要。

为了解决视频人脸识别问题，学者们提出了许多相关方法。例如，文献［6］提出了一种基于流形到流形之间距离的方法，一定程度上解决了视频人脸识别问题，提高了识别率。通常，非线性流形方法表示图像集为一个局部线性子空间的组合［7］。基于图像集的表示法，集之间的距离可以定义为这2个图像集中的2个“范例”(即样本平均)之间的距离。文献［8］通过横跨图像集样本的仿射或凸包特征化每个图像集，选择2个距离最近的点(1个包上1个点)作为“范例”。非参数化方法的另一类集间距离是通过比较非参数化模型的结构得到的，例如，广泛应用于文献［9］的典型相关分析，分析了线性子空间之间的主角度和正则关系。文献［10］通过一种包含4个状态的模型(中立-发生-极限-偏移)对面部表情序列进行建模。文献［11］提出一个图像集人脸识别方法:稀疏近似最近点(SANP)，该方法将每个图像集建模成1个仿射包，选择2个距离最近的点(每个图像集中1个点)作为稀疏近似最近点(SANP)，其中要求SANPs是由原始样本稀疏表示的，最终集之间的距离就是SANPs之间的距离乘以仿射包的维度。SANP相比于以前的算法，能得到更先进的性能［12］。基于面部水平曲线的3D 视频表情识别方法，文献［13］通过使用Chamfer距离比较跨帧的曲线从而提取出时空特征，同时使用了一种基于HMM的决定边界焦点算法进行分类。然而，现有3D人脸识别方法往往偏向于从3D视频中提取特征，但这些方法无法用在正式的视频人脸识别系统中［14］。

基于上述分析，为了解决传统的3D人脸识别方法中存在的问题，提出了一种基于视频分块聚类的格拉斯曼流形［15］自动识别系统，能够从3D视频中识别出6种不连续的面部表情、姿态及光照变化，实验结果表明了本文方法的有效性及可靠性。

1 相关工作

1.1 格拉斯曼流形上的谱聚类

聚类可以概况为:给定一组点{x1，x2，…，xn}并给出每对点的相似度比较，将所有点划分成群组，这样同一组中的点是相似的，而不同组内的点不相似。

根据定义，流形是一种拓扑空间，其局部与欧式空间相似。格拉斯曼流形是in的所有线性子空间的空间。目前格拉斯曼流形上的聚类技术在聚类算法(例如K-means)每次迭代时都需要计算流形上点的距离和平均。格拉斯曼流形上计算平均和聚类的方法可以大致分为内在的和外在的。内在的方法完全局限于流形本身，而外在方法可将流形上的点嵌入欧式空间并使用欧式度量进行计算。无论是使用内在或外在的方法进行迭代过程计算(例如K-means)都十分耗时，且计算量很大。

使用谱聚类可避免格拉斯曼上的迭代计算，聚类的问题可以简化为图拉普拉斯矩阵的特征向量分解。针对格拉斯曼的一组点{U1，U2，U3，…，Un}的完整的谱聚类算法如算法1。首先，计算出图拉普拉斯矩阵L∈in×n，该矩阵信息丰富，携带了流形上所有点对的相似性得分。如前文所述，格拉斯曼上的点是in的d维子空间，计算中，这些点保存在高瘦的正交化矩阵in×d中，可使用典型相关分析计算格拉斯曼流形上每对点的相似度。一种计算两点U1和U2的典型相关的有效方法是对U2=Q12ΛQ21进行奇异值分解，典型相关是对角矩阵Λ的奇异值。谱聚类的理论表明规范化的图拉普拉斯矩阵更合适，聚类的效果更佳。对于矩阵L，其规范化的图拉普拉斯为Lnorm=，其中D是对角度矩阵，其第i个对角元素等于L中第i行所有元素的总和。计算Lnorm之后，按照算法1所示的步骤继续完成聚类过程。与现有的聚类算法不同(其每一次迭代都需要计算格拉斯曼流形上的均值和距离)，提出的谱聚类算法将该问题缩减到一个低维的欧式空间中，所以聚类过程更加快速、有效。与最近发表的一种在格拉斯曼上聚类的方法相比，所提谱聚类算法在运行速度上比它快大约10～15倍。

算法1:在格拉斯曼上的谱聚类。

输入:流形上的点:{U1，U2，U3，…，Un}。

1)计算图拉普拉斯矩阵L∈in×n;

3)计算Lnorm的首个m特征向量;

4)令V∈in×n包含Lnorm的m特征向量;

输出:聚类:{C1，C2，…，Ck}，其中Ci={j|yj∈Ci}。

1.2 规范化3D视频数据库

通过完全自动化的面部规范化过程使得视频中所有网格的大小和分辨率都一致，图1所示为3D面部规范化过程的框图，细节过程在下文给出。以点云矩阵Pm×3表示3D面部，其中m是点的总数，P的每一行对应于一个点(顶点)的x，y，z坐标。3D面部图像包含孤立点，如图1a中圈出的区域所示，找出所有点深度zi的均值μ=和标准偏差可以去除孤立点，任何深度超出μ±3σ极限的点可视作为孤立点被过滤掉，成功探测出鼻尖之后，以鼻尖为中心半径范围r(r=85 mm)裁剪面部，图1d展示了裁剪出的3D面部，采用与文献［7］中相似的技术进行姿势纠正，计算出点云矩阵P的均值向量和协方差矩阵C=对协方差矩阵的主元分析(PCA)得到特征向量矩阵V，用来使点云矩阵P沿它的主轴对齐，其中P′=V(P－μ)。姿势纠正点云再次重新采样成统一的方形网格160×160，分辨率为1 mm。

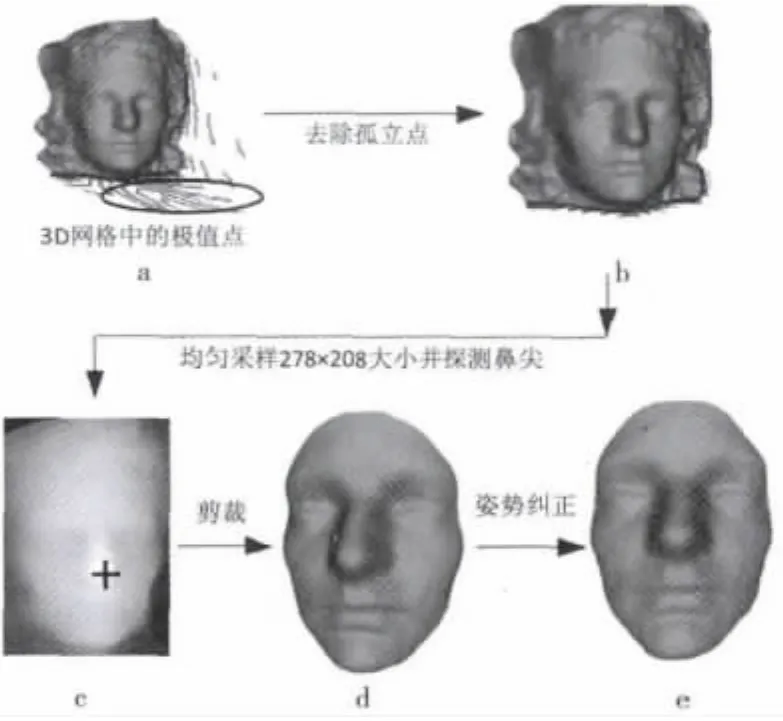
图1 3D面部图形规范化

2 方法提出

所提的基于3D视频的面部识别系统的完整流程如图2所示，线下训练阶段，系统从训练视频的不同位置提取视频片段，分别学习6类的表示;线上测试阶段，通过类代表获得提取的检索视频片段的相似度，同时使用一种基于表决的策略来决定检索脸部的类别。视频的总体模式包含这些片段:中立，紧接着是发生、极限和偏移。肉眼观察数据库中的视频时，注意到“中立-发生-极限-偏移”的次序并不一定适用于每个视频。例如，一些视频开始于表情的发生阶段，跳过了中立阶段，或者在一些视频中，执行者可能不回到表情的偏移阶段。因此，将完整视频序列作为一个整体进行建模可能导致性能降低，需要在视频的不同位置提取不同长度的局部视频片段。

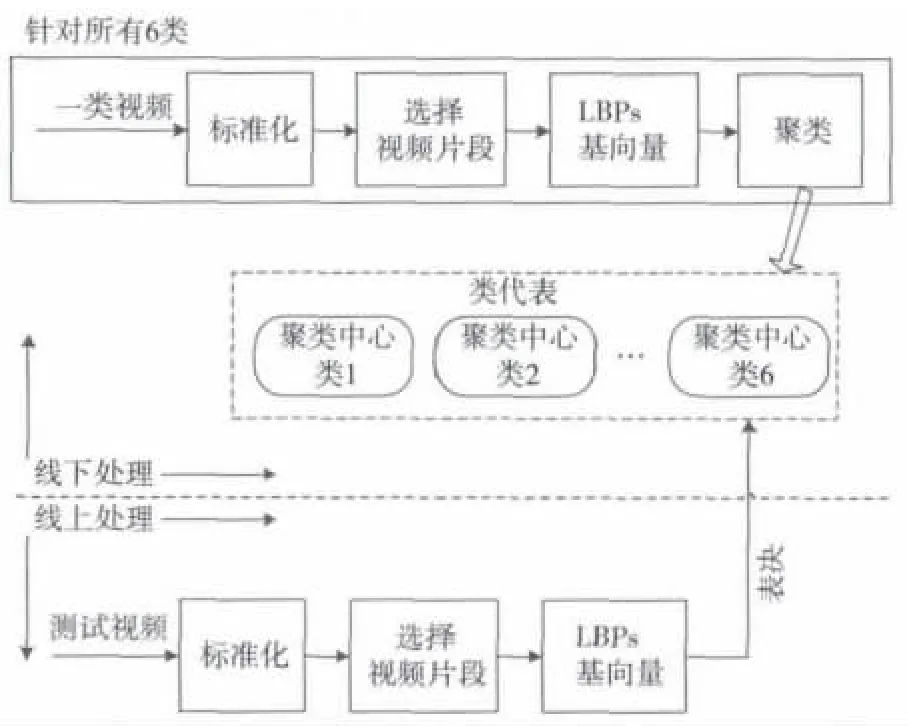
图2 基于3D视频的面部识别系统框图

针对给出的包含n帧的规范化视频序列V=［f1，f2，f3，…，fn］，使用一个可变长度的滑动窗口沿着序列提取视频片段。使用不同长度的滑动窗口的动机来自于观察，如果某人在特定的帧数量期间内执行一种表情活动，另一个人可能在不同的帧数量期间内执行相同的表情活动。

每个提取出的视频片段被表示成一个矩阵X=［f1，f2，f3，…，fm］∈ i25600×m，该矩阵的列对应于视频片段的 m帧的栅格扫描深度值。将X减去均值可以丢弃身份信息，仅保留所需的X的变形信息。通过X′=USVT可得到结果矩阵X′=X-μ的奇异值分解(SVD)。U的列形成正交单位向量组，可视作为基向量。这些基向量按重要性降序排列，携带了视频片段中包含的重要的表情变形信息。图3显示了顶层4个基向量，分别对应于从高兴、悲伤和惊讶这3种表情中提取的视频片段的顶层4个奇异值。

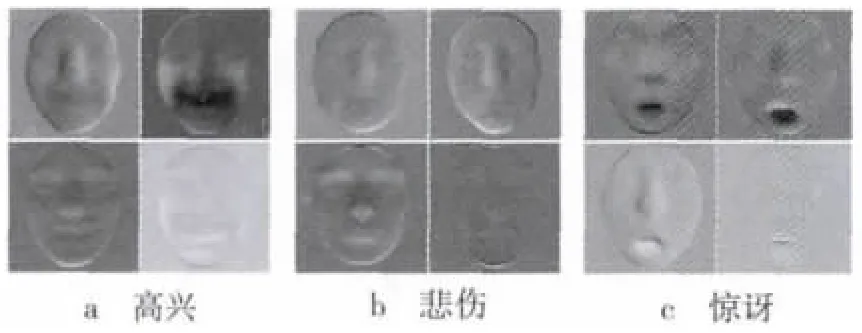
图3 从高兴、悲伤和惊讶3种表情中提取的视频片段的顶层4个基向量

这些基向量的集合(包含了U中顶层基向量的高瘦的标准正交矩阵)可视作为格拉斯曼流形上的点。因为本文方法仅考虑顶层的4个基向量，所以点位于G25600，4，很明显，G25600，4的维度很大，需占用大量内存。用局部二值模式(Local Binary Pattern，LBP)［3］的直方图替换视频片段矩阵X的深度值就可以克服这个问题。将X中的每一帧划分成4×4的非重叠块，针对每个块计算的直方图i59。所有块的直方图是级联的，帧由i944的特征向量所表示，导致点位于 G944，4而不是 G25600，4。

通过如上过程可获得视频的流形上的点，针对从一类表情的训练视频中提取的所有视频片段都执行相同的过程，计算出格拉斯曼上的点。接着对这些点进行聚类，相似度图拉普拉斯矩阵L显示出一些点与其他点大不相同，这些点来自于视频中表情表现为不正确或不一致的部分。因此，对于每一类表情仅考虑最相似的200个点，并将它们组成10个集群，计算出每个集群的均值。最后，将10个集群的中心视为类表示，并将其使用在分类步骤中。

按照相似的过程，可计算出所有6类表情的类表示，给定查询视频，对其归一化和提取视频片段之后，将视频片段视作G944，4上的点。使用基于决策的策略决定查询视频的类别。使用典型相关，可计算出类表示中查询视频的所有点的相似度。每个点只能对与其最相似的类表示投票。最后，得到投票数最多的类就视为查询视频的类别。

3 实验

所有实验均在4 Gbyte内存Intel Core 2.93 GHz Windows XP计算机上完成，编程环境为MATLAB 7.0。

3.1 实验建立

使用3个基准图像集数据库包括Honda/UCSD［7］、CMU Mobo［12］和 YouTube 数据库［15］评估本文方法，使用Viola和Jone的人脸探测器检测3个数据集的所有人脸图像，对于Honda/UCSD和YouTube数据集，直方图均衡化之后人脸图像大小分别裁剪为20×20和30×30，直接使用每个图像的原始像素值作为数据矩阵中的特征。对于CMU Mobo数据集，提取LBP特征直方图作为脸部特征。每个数据集，分别以帧数目为50、100和200执行3次实验，需要注意分类使用的所有图像是否集中的帧数目少于给定的帧数目。

将本文方法与几个先进的有代表性的图像集分类方法做了比较，其中判别典型相关分析(DCC)［9］和互空间方法(MSM)［2］是线性子空间方法，流形到流形距离(MMD)［6］和流形判别分析(MDA)［7］是非线性流形方法，基于图像集距离的 仿 射 包 (AHISD)［8］、基 于 图 像 集 距 离 的 凸 包(CHISD)［8］和稀疏近似最近点(SANP)［11］都是仿射子空间方法。所有这些方法都使用各自作者提供的源代码实现，根据原文出处建议的参数调整得到最佳结果，对于AHISD、CHISA和SANP，本文使用它们的线性版本，因为本文没有考虑本文方法的核版本。在Honda/UCSD和CMU Mobo数据集，每个类有一个单个训练图像集，为DCC将每个单一训练图像集划分成两个子集去构建类内集。

3.2 实验结果和分析

3.2.1 Honda/UCSD数据集

Honda/UCSD数据集包含20个不同对象的59个视频序列，对于每个对象，不同序列中会有不同的姿态和表情，如图1中的人脸图像，使用20个序列进行训练，剩余的序列用于测试。

不同训练帧得到的识别结果见表1，可以清楚地看到，本文方法在所有情况下都能得到最佳性能，尤其是当帧数目为200时，可以正确识别所有测试集，线性本文方法输出结果优于SANP，甚至与SANP的核版本有相同的性能。当每个图像集有足够多图像样本时，所有方法都能得到良好的性能，除了MSM，通常得到的结果较差，当图像样本数目不高时(如50)，非线性流形方法(如MMD)不能得到高识别率，然而，基于仿射子空间的方法的性能一直保持良好。

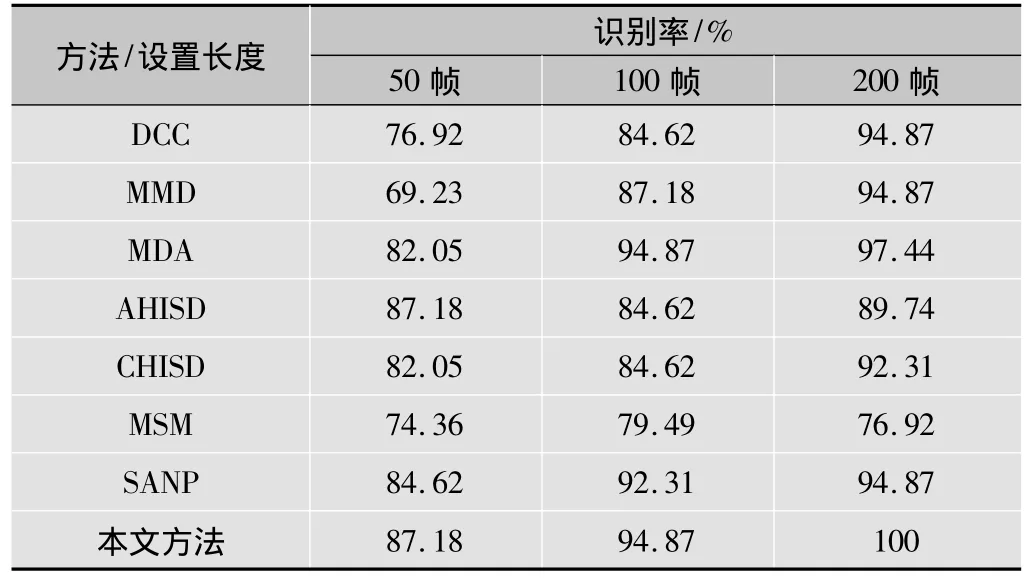
表1 在Honda/UCSD数据库上的识别率

3.2.2 CMU Mobo数据集

CMU Mobo数据集包含24个对象在跑步机上行走的96个序列，对于每个对象，有4个分别包含4种行走模式的视频序列(有明显的姿态变化)。采用的样本特征为均匀LBP直方图，使用圆形(8，1)邻域从8×8方形灰度图像中提取得到，随机选择每个对象的一幅图像用作训练数据，剩余图像集作为测试数据。

执行了10个实验，平均识别率和标准差列于表2，所有情况下，本文方法都能得到最高的识别率，尽管SANP和CHISD与本文方法的识别精度接近，但在3.3节的运行时间比较中可以看到，本文方法的运行时间远少于SANP和CHISD。当只有50帧时，DCC、MSM和MDA的识别率低于90%，这可能是由于判别信息提取和流形分析依赖于每个图像集有足够多图像样本的事实导致的，相比于AHISD，本文方法的优点是显著的。

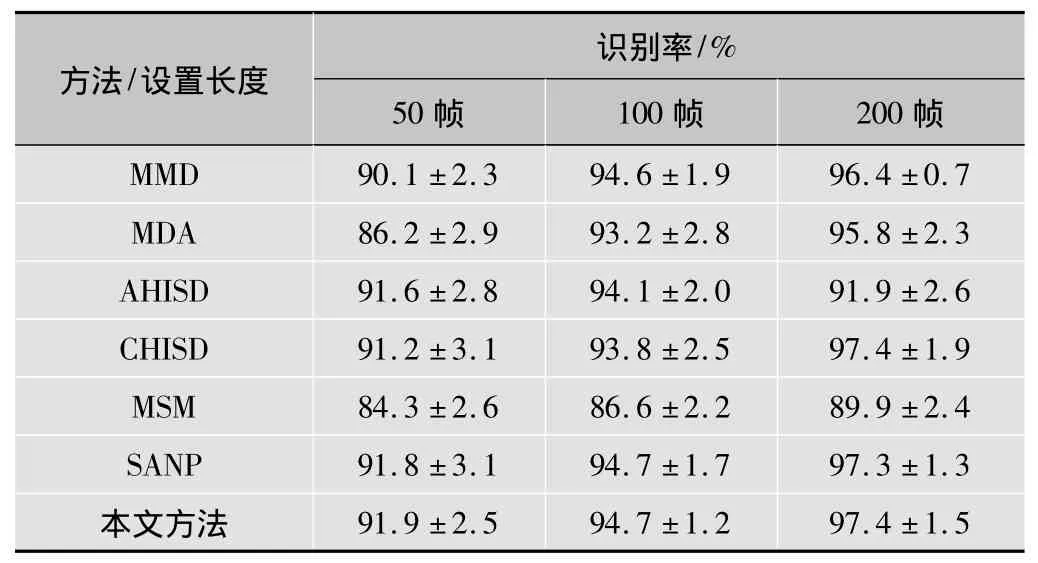
表2 在CMU Mobo数据库上的识别率

3.2.3 YouTube数据集

YouTube数据集是一个大规模的视频数据集，这个数据集比前两个数据集更具挑战性，因为数据集中的图像大部分分辨率低，且有大的姿态、表情变化或运动模糊等，如图4所示。在这部分，使用视频序列的前29个明星做实验，对于每个对象，随机选择3个视频序列用作训练数据，从剩余序列中再随机选择3个序列用作测试数据。利用重复随机选择的测试数据，执行了5个实验。

图4 YouTube数据集上的图像示例

实验结果，包括识别率和标准差均列于表3。得到的结论与前两个数据集相似，本文方法比其他方法的性能更好，相比于第二好的方法SANP，当帧数目为50和100时，得到超过1%的性能提高。在这个具有挑战性的数据集上，MSM的结果最差，平均识别率低于70%，有趣的是，AHISD的识别率会随着帧数目的增加而波动，同前两个数据集中得到的结果类似。

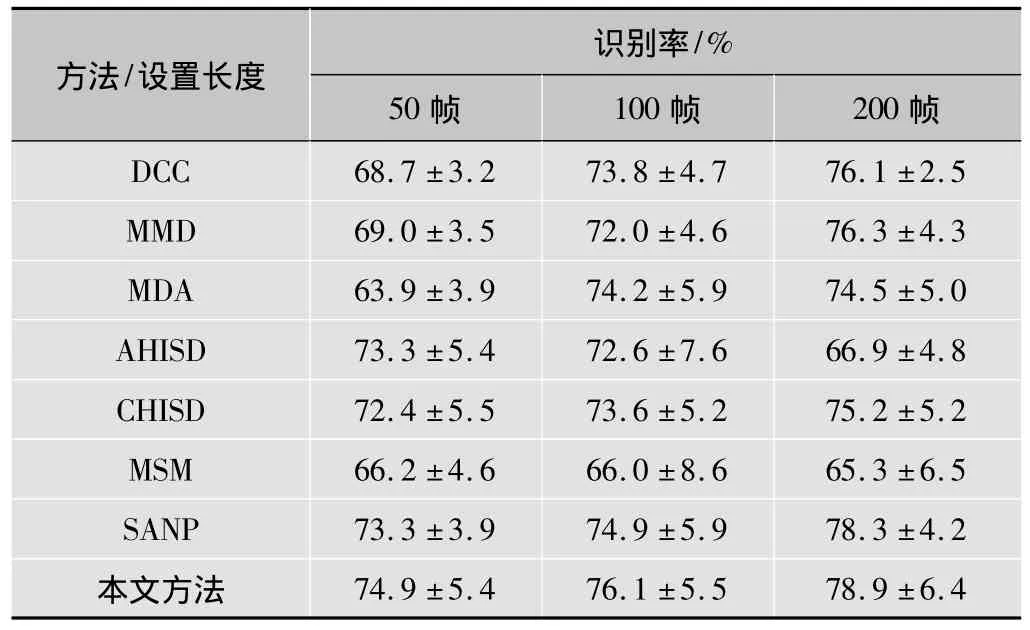
表3 在YouTube数据库上的识别率

3.3 性能比较

本文方法能得到比其他方法更高的识别率，包括最近开发出的SANP，接下来比较它们的运行时间，这是实际应用中最重要的内容。

在CMU Mobo数据集上进行人脸识别，实验设置同3.2节，编程环境是MATLAB 2001a版本，平台使用i7的2.8 GHz CPU，4 Gbyte RAM，为了使运行时间比较更为公平，本文也列出了一些方法的离线训练时间，除了这些判别方法(即DCC、MDA)需要一个训练阶段，MMD构建局部线性子空间，SANP训练集SVD，本文方法中学习训练集的投影矩阵都视为离线训练。

分类图像集，帧数为100的离线训练时间和在线测试时间都列于表4，本文方法离线训练时间很短，因为仅需要进行几个矩阵的求逆计算，在线测试时间对分类器来说更重要。

表4 各算法在CMU Mobo数据库上对100帧图像的训练时间

从表4可以看出，本文方法的运行时间(即分类测试图像集时间)远小于其他几种方法，相比于SANP，本文方法是其速度的20倍，本文方法比第二快的方法MDA还要快5倍，且识别精度远高于MDA。

为了更全面地评估运行时间，表5所示为各算法在各种帧数目时的测试时间。

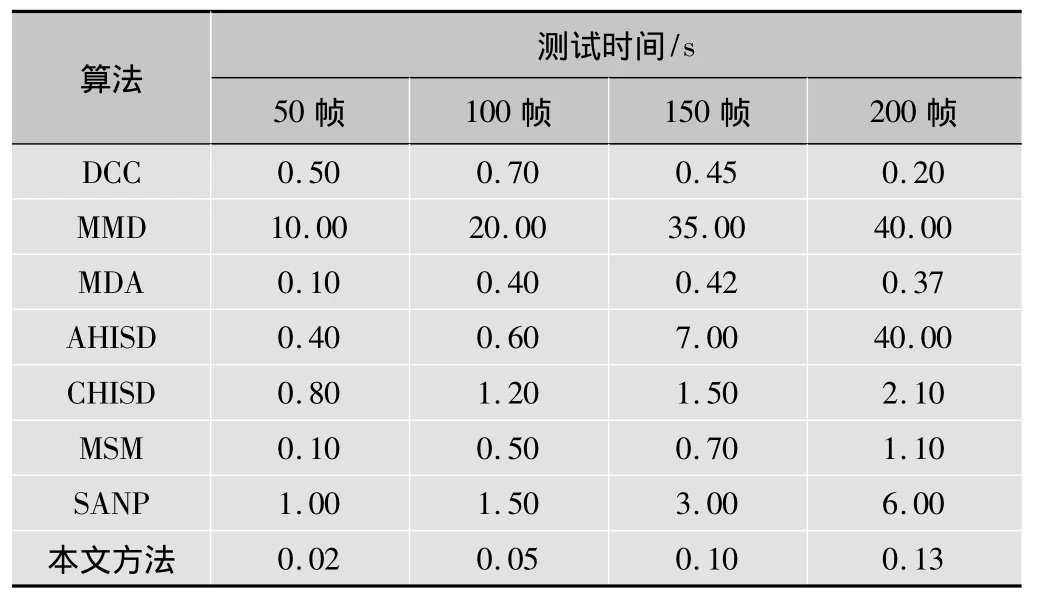
表5 各算法在CMU Mobo数据库上对应各个帧数的测试时间

从表5可以看出，除了一些特殊情况(如DCC和MDA当帧数为200时)，所有算法的测试时间都随着帧数增加而增加，AHISD算法增加最为明显，无论帧数取何值，本文方法所耗测试时间总是最少，体现了本文方法的高效性。

4 结束语

针对传统的3D人脸识别方法仅考虑特征提取而不能很好地运用于实际视频人脸识别系统的问题，提出了一种从3D视频中自动识别面部变化的系统。在规范化原始3D视频后，该系统从视频的不同位置提取出局部视频片段，并将它们表示在格拉斯曼流形上。利用谱聚类的优势和有效性，采用了对格拉斯曼流形上的点进行有效的聚类。分类中使用了一种简单的基于表决的策略。在大型通用视频数据库上测试了所提系统的性能，实验结果表明，与几种较为先进的方法相比，本文方法取得了更高的分类精度。此外，该系统无需任何用户协作或人工标记面部标注。

未来会考虑结合其他先进的方法，改变初始参数的设置，进行大量的实验，进一步改进本文方法的识别性能，从而更好地运用于3D实时视频识别系统。

［1］ 王巍，王志良，郑思仪，等.人机交互中的个性化情感模型［J］.智能系统学报，2010，5(1):10-16.

［2］ 许江涛.多姿态人脸识别研究［D］.南京:东南大学，2006.

［3］ 李晓莉，达飞鹏.基于排除算法的快速三维人脸识别方法［J］.自动化学报，2010，36(1):153-158.

［4］ 薛雨丽，毛峡，郭叶，等.人机交互中的人脸表情识别研究进展［J］.中国图象图形学报，2009，14(5):764-772.

［5］ 刘帅师，田彦涛，万川.基于Gabor多方向特征融合与分块直方图的人脸表情识别方法［J］.自动化学报，2011，37(12):1455-1463.

［6］ 刘忠宝，潘广贞，赵文娟.流形判别分析［J］.电子与信息学报，2013，35(9):2047-2053.

［7］ WANG R，SHAN S，CHEN X，et al.Manifold-manifold distance with application to face recognition based on image set［C］//Proc.IEEE Conference on Computer Vision and Pattern Recognition，2008.［S.l.］:IEEE Press，2008:1-8.

［8］ WANG R，GUO H，DAVIS L S，et al.Covariance discriminative learning:a natural and efficient approach to image set classification［C］//Proc.IEEE Conference on Computer Vision and Pattern Recognition，2012.［S.l.］:IEEE Press，2012:2496-2503.

［9］ 侯书东.基于相关投影分析的特征提取研究及在图像识别中的应用［D］.南京:南京理工大学，2012.

［10］ SANDBACH G，ZAFEIRIOU S，PANTIC M，et al.Recognition of 3D facial expression dynamics［J］.Image and Vision Computing，2012，30(10):762-773.

［11］ HU Y Q，MIAN A S，OWENS R.Face recognition using sparse approximated nearest points between image sets［J］.IEEE PAMI，2012，34(10):1992-2004.

［12］ 葛微.自动人脸识别的关键问题研究［D］.长春:中国科学院长春光学精密机械与物理研究所，2010.

［13］ SANDBACH G，ZAFEIRIOU S，PANTIC M，et al.Static and dynamic 3D facial expression recognition:a comprehensive survey［EB/OL］.［2013-10-15］.http://dl.acm.org/citation.cfm?id=2380025.

［14］ 张鑫.基于SIFT算法的ATM视频人脸识别系统研究［D］.哈尔滨:哈尔滨工程大学，2012.

［15］ TURAGA P，VEERARAGHAVAN A，SRIVASTAVA A，et al.Statistical computations on grassmann and stiefel manifolds for image and videobased recognition［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2011，33(11):2273-2286.