多次压氦法和预充氦压氦法质谱细检漏方法研究
2014-02-07王庚林李宁博刘永敏
王庚林,李宁博,李 飞,刘永敏
(北京市科通电子继电器总厂有限公司,北京 100041)
0 引 言
密封电子元器件在生产至使用的全过程中,要经受多次密封性检测。若超出密封后的最长候检时间,则应采用一次或多次压氦的预充氦压氦法,进行密封性检测。
国内外的相关标准[1~3]规定,再次和多次采用压氦法细检漏时,不管相邻两次检测之间间隔时间多长,均采用与单次压氦相同的压力与时长,多采用1小时(标准文献[1]对不同内腔容积采用0.5小时或1小时)的最长候检时间,均采用相同的测量漏率判据。这对多次压氦法,n次检测的判据可能加严n倍;对预充氦压氦法,检测的判据可能加严几倍到几个数量级。而且还可能出现接近粗漏的大漏的漏检和细漏的错判。
在我国的相关行业标准[4]中,曾提出先细检漏,压氦后再细检漏,以后一次漏率的增加值为测量漏率。这种二次检测方法有一定的可行性,但会加大测试的偏差,而且丧失了多次压氦,特别是预充氦所形成的高灵敏检测特性。
薛大同等先生经过深入研究和持续的改进[5~7],提出了新的二次检测方法。该方法主要通过多因素比较前一次细漏检测和压氦后二次细漏检测的候检时长和测量漏率,从而判断样品密封性是否合格。但前后进行两次细漏检测,加大了检测的工作量,并且判定的过程相当复杂,不利于实施和操作。
本研究在以严密等级τHemin为基本判据[8]的基础上,通过分析研究多次压氦或预充氦后再压氦对测量漏率的影响,确定再次压氦的时长,采用一次压氦细检漏检测的方法,准确地确定最长候检时间,给出细漏检测的测量漏率判据,使密封性是否合格的判定更便捷。
1 多次压氦法的内部氦气分气压和测量漏率公式
密封件初次压氦后经一定时间间隔至再次压氦前的内部氦气分压为
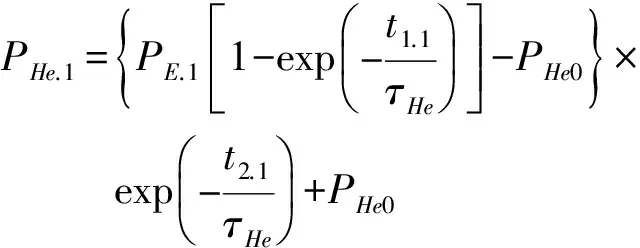
(1)
式中,PE.1和t1.1为初次压氦的压力和时间;t2.1为初次压氦至二次压氦的时间;PHe0为空气中氦气分气压,PHe0=0.533 ppm;τHe为被检件的氦气交换时间常数。
若此时细检漏,则测量漏率为
(2)
经再次压氦候检,细检漏时的内部氦分压为
(3)
式中,PE.2和t1.2为二次压氦的压力和时间;t2.2为二次压氦后的候检时间。
此时,二次压氦后细检漏的测量漏率为
(4)
忽略PHe0,考虑每次压入的氦的积累作用,经n次压氦和候检,氦质谱细检漏时的测量漏率R11.n为

(5)
式中,PE.i和t1.i为i次压氦的压力和时间;t2.in为第i次压氦结束至n次压氦结束的时间;t2.n为n次压氦后的候检时间。当t2.in大于5τHemin时,可以忽略第i次及之前压氦的作用。
当τHe为严密等级τHemin时,式(2)的R1即为初次压氦和候检后细检漏的测量漏率判据R1max;式(4)的R11.2即为二次压氦和候检后细检漏的测量漏率判据R11.2max;式(5)中的R11.n即为n次压氦和候检后细检漏的测量漏率判据R11.n.max。
2 多次压氦法的压氦条件和细漏检测最长候检时间
2.1 压氦条件和最长候检时间的问题
依据式(1)~式(4)做出二次压氦法R11.2(R1)~τHe典型关系曲线,如图1所示。

图1 多次压氦法典型R11 (R1)~τHe关系曲线族
其中二次压氦后的最长候检时间t2.2max采用参考文献[8]中的t2max式(8a)进行计算。
由图1曲线4可见,当再次压氦时长大于一定值、最长候检时间按单次压氦取值时,在τHemin附近,R11.2~τHe曲线呈递减趋势,不会出现错判;但对图中AB间大于且接近τHe0的大漏,会出现漏检。从曲线7可见,当再次压氦时长不足时,不仅会出现CD间大漏的漏检,在τHemin附近,R11.2~τHe曲线会出现波折,EF间的细漏会错判为合格,FG间的细漏会错判为不合格。错判和漏检,都是密封性检测所不能允许的,应当寻求解决的办法。
2.2 压氦时长的确定
依据式(5)、经相似图1的拟合作图证明,后面“2.4”还将验证,取压氦时长t1.i为
(6.1)
式中,PE.i-1和t1.i-1为前一次压氦的压力和时间。
当忽略PHe0时,可保证i次压氦后,只要候检时间t2i不大于由后面式(9.2)给出的t2i.max,测量漏率R11.i~τHe曲线在τHe≥τHe0、τHe<τHemin的范围呈单峰状,并在τHemin的一侧,当τHe增加时,可实现R11.i的递减,从而避免细漏的错判。
工程实施中为了简便和保险,除非t1.i-1很长,一般取
(6.2)
2.3 最长候检时间的确定
经n次压氦后,τHe=τHe0被检件的内部氦气分气压为
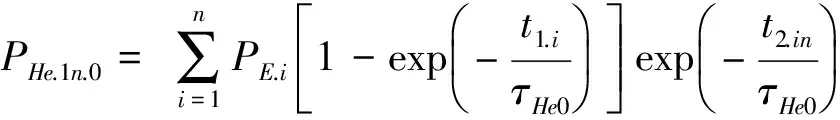
(7)
τHe=τHemin被检件内部氦气分气压为
(8)
设被检件的最长候检时间为t2n.max,则τHe=τHe0时的测量漏率R11.n和τHe=τHemin时的测量漏率判据R11.n.max应相等,即
由此可得最长候检时间t2n.max为
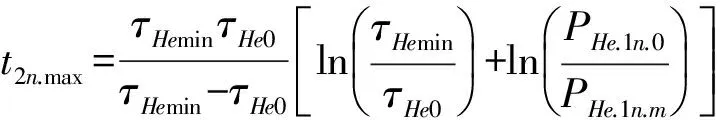
(9.1)
采用t2n.max,可以避免大于且接近τHe0的大漏的漏检。
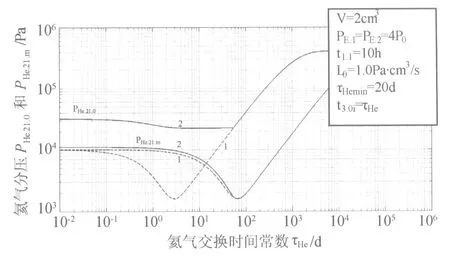
以二次压氦法为例,依据式(7)和式(8),比较PHe.12.0和PHe.12.m的大小,如图2所示。其中曲线1的t1.2依据式(6.1)取值,曲线2的t1.2依据式(6.2)取值。
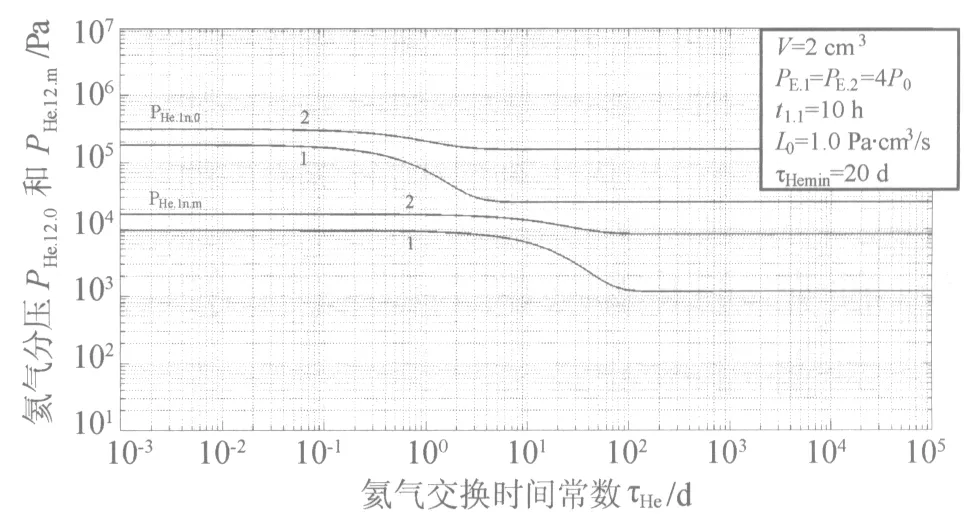
图2 氦气分压PHe.12.0、PHe.12.m~τHe关系曲线
从图2可见,PHe.12.0始终大于PHe.12.m,即式(9.1)中的ln(PHe.1n.0/PHe.1n.m)始终大于零。为了简便和保险,可取
(9.2)
即t2n.max可按参考文献[8]中预充氦法最长候检时间t3max式(9a)取值。
2.4 验证
采用作图法进行公式验证,单次压氦法测量漏率R1依据参考文献[8]公式(3)和本文式(1)、(2),多次压氦法测量漏率R11.2依据式(3)、(4)和(5)确定的典型R11.2(R1)~τHe关系曲线,如图3所示。

图3 多次压氦法典型R11.2(R1)~τHe关系曲线
由图3曲线可验证:对二次或多次压氦法氦质谱细检漏,只要各次压氦时长按式(6.1)或(6.2),压氦后最长候检时间t2n.max按式(7)、(8)和(9.1)或按(9.2),测量漏率判据按式(1)~(4)或(5),并与粗检漏相结合,可进行τHemin的判定性检测,不会发生接近粗漏的大漏的漏检和细漏的错判;同时,对正确确定细检漏的测量漏率判据,忽略PHe0的式(5)适用。当粗检漏通过,细检漏R11.n 从图3还可见,对首次压氦后再进行i次压氦,若压氦压力、时间相等且间隔时间t2.1i<2τHemin,则测量漏率判据与单次压氦相比,会接近i倍。 当元器件密封时预充氦,首次检测采用氦质谱细检漏,之后压氦再检测或超出最长候检时间时压氦再检测,密封后经时间间隔t3.01至压氦前的内部氦气分压为 (10) 式中,k为预充氦比,即预充气体中氦气分压与P0之比。 若此时细检漏,则测量漏率为 (11) 经压氦候检,细检漏时的内部氦分压为 (12) 式中,PE.1和t1.1为压氦压力和时间;t2.1为压氦后候检时间。 此时,测量漏率为 (13) 忽略空气中的氦气分气压PHe0,则R21.1可简化为 (14) 依此类推,可以得到预充氦再经n次压氦后,氦质谱细检漏的测量漏率R21.n为 (15) 式中:t2.n为n次压氦后的候检时间;t3.0n为预充氦密封结束至n次压氦结束的间隔时间;t2.in为i次压氦结束至n次压氦结束的间隔时间。 当τHe等于严密等级τHemin时,式(11)~(15)中的R2、R21.1或R21.n即为测量漏率判据R2max、R21.1.max或R21.n.max。 按式(10)~(13)绘制预充氦后压氦的R21.1(R2)~τHe关系曲线,如图4所示,其中预充氦后的最长候检时间t3max依据参考文献[8]式(9a)计算。 压氦后的最长候检时间t21.max仍依据参考文献[8]t2max式(8a)进行计算。 图4 预充氦压氦法R21.1(R2)~τHe典型关系曲线族 由图4中曲线4可见,当压氦时长大于一定值、最长候检时间按单次压氦取值时,在τHemin附近R21.1~τHe曲线呈递减,不会出现错判;但对于图中AB段大于且接近τHe0的大漏,会出现漏检。从图4中曲线7可见,当压氦时长不足时,在τHemin附近,R21.1~τHe曲线会出现波折,以R21.1max为判据,CD间的细漏会错判为合格,DE间的细漏会错判为不合格。错判和漏检,都是密封性检测所不能允许的,应当寻求解决的办法。 依据参考文献[8],忽略PHe0,当t3=τHe时,τHe处的R2处于峰值为R2.M, 可得 从而有 (16.1) 式中,PE.i为i次压氦压力;t3.0i为预充氦密封结束至i次压氦结束的间隔时间。 当忽略PHe0时,可保证i次压氦后,只要候检时间t2i不大于由后面式(19.2)给出的t2i.max,测量漏率R21.i~τHe曲线在τHe≥τHe0、τHe<τHemin的范围呈单峰状,并且在τHemin的一侧,当τHe增加时,可实现R21.i的递减,从而避免细漏的错判。 工程实施中为了简便和保险,也为确定最长候检时间,应取: t1.i≥1.2 h (16.2) 忽略PHe0,预充氦经n次压氦后,τHe=τHe0时被检件的内部氦气压力为 (17) τHe=τHemin时被检件的内部氦气压力为 (18) 设预充氦后再经历n次压氦,被检件最长候检时间为t2n.max,则τHe=τHe0时的测量漏率R21.n和τHe=τHemin时的测量漏率判据R21.n.max应相等,即 由此可得最长候检时间t2n.max为 (19.1) 采用此t2n.max,则可以避免大于且接近τHe0的大漏τHe的漏检。 依据式(17)、(18),以式(16.1)和(16.2)为t1.i条件,做出预充氦一次压氦后的PHe.21.0~τHe及PHe.21.m~τHe关系曲线,如图5所示。其中曲线1按式(16.1),曲线2按式(16.2)。 图5 氦气分压PHe.21.0、PHe.21.m~τHe关系曲线 从图5可见,t1.i采用联立式(16.1)和(16.2)的条件,PHe.21.0始终大于PHe.21.m,式(19.1)中的ln(PHe.2n.0/PHe.2n.m)始终大于零。为了简便和保险,同样可取 (19.2) 此式(19.2)同式(9.2),即t2n.max可按参考文献[8]中预充氦法最长候检时间t3max式(9a)取值。 依据前面分析,预充氦法测量漏率R2依据参考文献[8]式(6)和本文式(10)、(11),预充氦压氦法测量漏率R21.n依据本文式(12)、(13)和(14)确定的R21.1(R2)~τHe典型关系曲线,如图6所示。 图6 预充氦压氦法R21.1(R2)~τHe典型关系曲线族 图6已相对全面的验证,对预充氦压氦法氦质谱细检漏,预充氦密封后经不同的间隔时间t3.0i再压氦,压氦时长t1.i按联立式(16.1)(16.2),压氦后最长候检时间t2n.max按式(17)、(18)和(19.1)或按式(19.2),测量漏率判据按式(10)~(13)或(14)(15),并与粗检漏相结合,可进行τHemin的判定性检测,不会发生错判和漏检;同时对正确确定细检漏的测量漏率判据,忽略PHe0的式(14)、(15)适用。当粗检漏通过,细检漏R21.n 由图6还可见,预充氦后再压氦,当间隔时间t3.0i小于τHemin时,在τHemin处,预充氦经衰减的氦分压一般远高于压氦压入的氦分压,所以判据R21.nmax可能会比仅压氦的判据R1max高出几倍甚至几个数量级。 通过对多次压氦法及预充氦压氦法的分析研究,采取理论推演和曲线拟合相结合的方法,给出了再次或多次压氦的压氦时长条件,既可保证τHe≥τHe0时测量漏率R~τHe曲线呈单峰值,并在τHemin一侧单向递减,又可保证压氦后τHe0被检件的内部氦气分气压不低于τHemin被检件,使最长候检时间式(9.2)(19.2)适用,既可避免细漏的错判,又可避免大漏的漏检,从而提出了正确确定压氦时长、细漏检测最长候检时间和测量漏率判据的方法。只要能保存或获取被检件以往的检漏历史数据,如密封日期和时间、预充氦比k、各次压氦检漏的日期和时间、压氦的压力和时长,便可采用本项研究的成果,一次压氦和细漏检测,并加粗检漏,更为便捷准确地进行密封电子元器件密封性是否合格的判定。目前,此研究成果已经申请发明专利“一种多次压氦和预充氦压氦的氦质谱细检漏方法”,并已获中国国家知识产权局受理,申请(专利)号是201310161154.4,敬请相关专家和科技工作者予以关注、推敲、指正和应用。 对本文氦气分气压和测量漏率式的推演,工信部电子四所安琪先生曾提出过正确的改进建议,在此表示衷心的感谢。 [1] MIL-STD-750-1 Department of Defense Test Method Standard Test Methods for Semiconductor Devices Method 1071.9 Hermetic Seal[S].2010. [2] MIL-STD-883J Second Draft Department of Defense Test Method Standard Microcircuits Method 1014.14 Seal[S].2012. [3] GJB548B-2005 微电子器件试验方法和程序[S]. [4] QJ3212-2005 氦质谱背压检漏法[S]. [5] 薛大同.氦质谱检漏仪背压检漏标准剖析及非标准漏率计算程序[J].真空科学与技术学报.2005(12):20-26. [6] 薛大同,肖祥正,李慧娟,等.氦质谱背压检漏方法研究[J].真空科学与技术学报.2011(1):105-109. [7] 薛大同,肖祥正,王庚林.密封器件压氦和预充氦细检漏判定漏率合格的条件[J].真空科学与技术学报.2013(8):735-743. [8] 王庚林,李飞,王彩义,等.氦质谱细检漏的基本判据和最长候检时间[J].中国电子科学研究院学报.2013,8(2):213-219.3 预充氦压氦法的内部氦气分气压和测量漏率公式
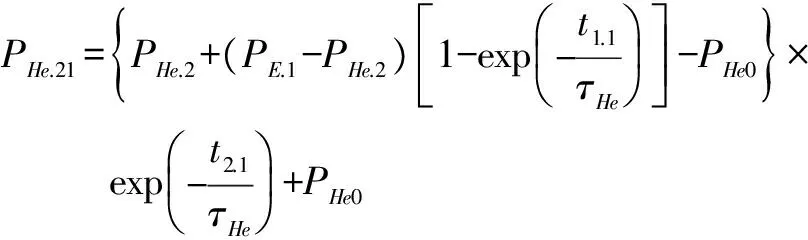

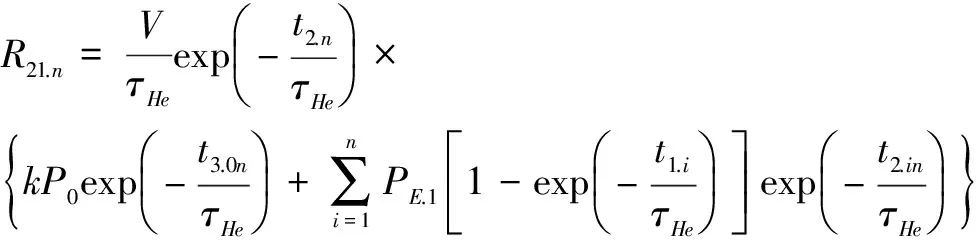
4 预充氦压氦法的压氦条件和细漏检测最长候检时间
4.1 压氦条件和最长候检时间的问题

4.2 压氦时长的确定
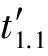
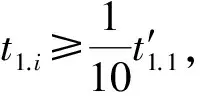
4.3 最长候检时间的确定

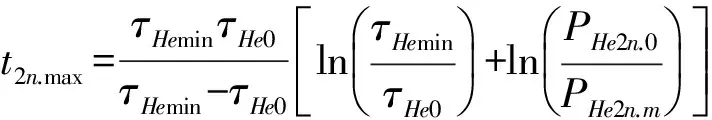
4.4 验 证

5 结 语
