基于脉冲相位线性度的雷达辐射源信号分选

郭利荣，何明浩，郁春来，王冰切

(空军预警学院，武汉 430019)

0 引 言

现有侦察装备主要利用常规五大参数进行信号分选[1]。脉内特征作为分选特征参数是近年来人们形成的一种普遍共识[2～7]，相对常规参数而言，利用其对雷达辐射源信号进行分选，可以大大提高分选结果的准确率与稳定性。随着信号环境的日益复杂、新型复杂体制雷达的不断涌现、信号形式的多变快变，提取此类信号脉内特征的难度与误差都会增加，会直接导致分选准确率的降低。相参特性就是指相邻脉冲相位具有确定的关系[8]，且相参特征在某一规定时间和空间内不会随着频率、调制方式、发射波形、功率等变化而变化[9]，具有其他特征参数无可比拟的优势，因此，研究利用雷达信号相参特征的分选方法，对提高现役雷达对抗侦察装备信号分选能力，为告警、引导干扰和反辐射攻击等提供可靠的情报数据来源，具有十分重要的应用价值。

基于相参特征所具有的优点，通过检测脉冲相位与时间是否存在线性关系来判别信号的相参性，将此方法应用于雷达辐射源信号分选中。对接收的脉冲信号，提取任意两脉冲的相位差序列，求取相位差序列的离差序列，若离差落入一定的判决门限，则认为这两个脉冲相位是线性的，脉冲是相参的，即脉冲来自同一辐射源，否则，认为脉冲相位是跳变的，脉冲是非相参的，即脉冲来自不同辐射源。

1 相参脉冲串的数学模型

雷达辐射源发射的相参脉冲串是通过对主振源产生的高稳定度连续载波信号进行脉冲调制得到的，也可以说，相参脉冲信号的产生是对连续正弦波信号以等间隔或非等间隔的方式截取[9]。相参脉冲串信号,如图1所示。

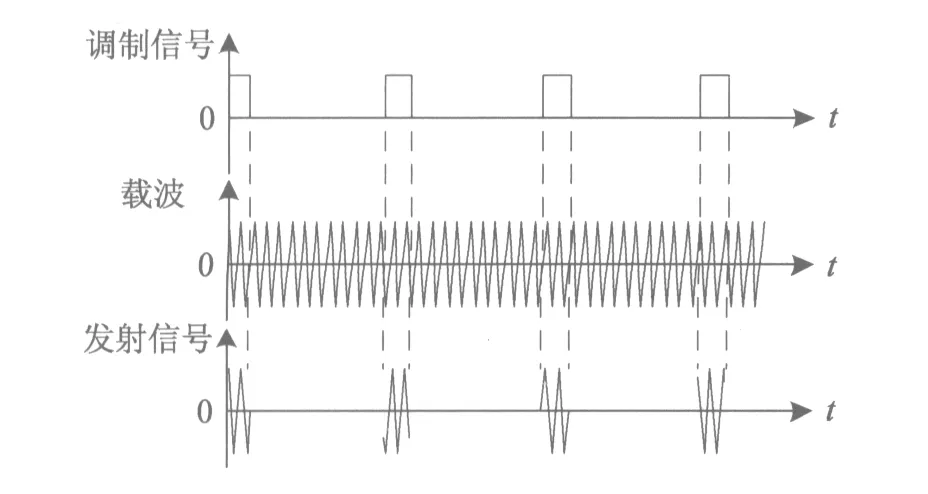
图1 相参脉冲串信号示意图

雷达辐射源发射的相参脉冲信号，经接收机的带通微波预选器、下变频混频器后得到中频信号，对各脉冲中频信号进行采样可得到

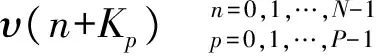
(1)

式中，Ap为第p个脉冲的幅度；φ0为整个观察期间恒定的初相；f为脉冲信号的频率；Kp为第p个脉冲的起始采样点，脉冲重复间隔Tr内的采样点数为K；ts为采样间隔；N为每个脉冲内的信号采样点数；υ是均值为0，方差为σ2的复高斯白噪声，满足[10]：

(2)

2 脉冲串相位线性度检测

相参脉冲信号可看作是连续波信号经矩形脉冲调制得到的，则相参脉冲串的脉冲相位与脉冲序号呈线性关系[11]。因此，可检测脉冲相位的线性度来判断脉冲是否相参，进而判别是否来自同一雷达辐射源，达到分选的目的。

2.1 频率初值估计

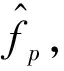
2.2 脉冲相位差序列

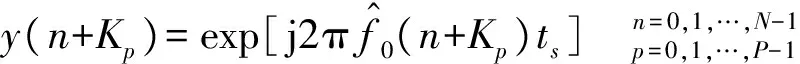
(3)

将式(1)和式(3)共轭相乘，得到的序列为

k(p)=s(n+Kp)y*(n+Kp)=Aexp{j[2πΔf0(n+Kp)ts+φ0]}+υ′(n+Kp)

(4)

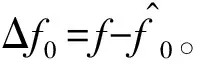
对序列k(p)进行脉内累加，得到一个长度为P的序列[13]为

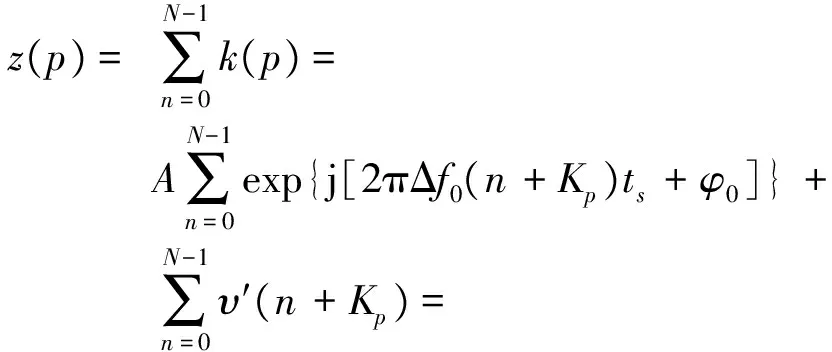
(5)

当信噪比较高时，加性噪声可折算为相位噪声，则式(5)可近似表示为[14]

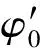
(6)

式中，ε(p)均值为0，方差为1/(2SNR′)的高斯过程。

将z(p)移位后再与z(p)共轭相乘，得到新的序列d(p)为

d(p)=z(p+1)z*(p)=

(A′)2exp{j[2πΔf0Tr+ε(p+1)-ε(p)]}=

(A′)2exp{j[Δφ(p)]}p=0,1,…,P-2

(7)

式中，Δφ(p)=2πΔf0Tr+ε(p+1)-ε(p)为d(p)的相邻脉冲相位差序列。由式可知，ε(p)和ε(p+1)是独立同分布的高斯过程，都服从于N[0,1/(2SNR′)]分布，故ε′(p)=ε(p+1)-ε(p)的分布为

(8)

2.3 相位线性度检测

当接收到的脉冲串信号是相参脉冲信号，信号模型可见式(1)；当接收到的脉冲串信号为非相参脉冲信号，信号模型可以表示为

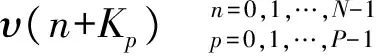
(9)

式中,φp第p个脉冲的初始相位，是(-π,π)内均匀分布的随机变量。

设序列d(p)相邻脉冲相位差Δφ(p)的离差为y(p)。

当接收到相参脉冲串信号时，得到相参脉冲相位差的离差为

y0(p)=Δφ(p)-E[Δφ(p)]

(10)

当接收到的信号是非相参脉冲信号，此时，脉内累加得到

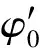
(11)

将z(p)移位后再与z(p)共轭相乘，得到相邻相位差序列为

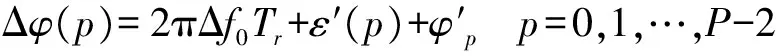
(12)

则脉冲相位差的离差为

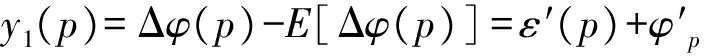
(13)

仿真实验1：假设侦察接收一串脉冲个数为P=2 000的相参脉冲信号，脉冲幅度A=1，采样频率为fs=100 MHz，脉冲重复间隔为Tr=100 μs，信号的频率为f=30 MHz，脉冲宽度为τ=2 μs，脉冲信号的初始相位φ0=π/3。取k=2.6～3.0[11]，即可确定判决门限T，按照设置的判决门限，判别脉冲串中相邻脉冲相位差的离差是否在判决门限内，根据落入判决门限的个数来计算相参信号识别的准确率。实验独立仿真100次，不同输入信噪比下相参信号识别准确率见表1,输入信噪比为7 dB时相邻脉冲相位差的离差,如图2所示。

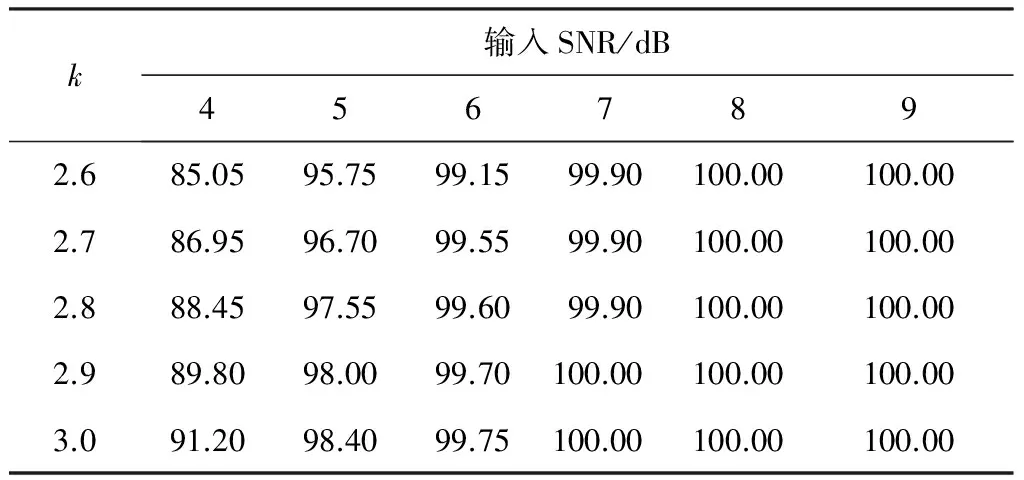
表1 不同输入信噪比下相参信号识别准确率(%)

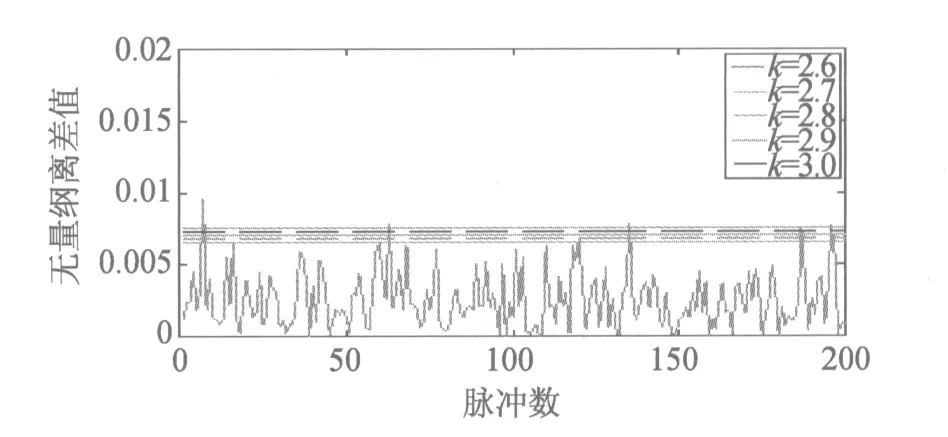
图2 输入信噪比为7 dB时相邻脉冲相位差的离差

从表1中可以看出，随着输入信噪比的增加，相参信号的识别准确率逐渐增加，达到一定信噪比后，识别准确率接近100%。随着k值的增加即门限值增大，相参信号的识别准确率逐渐增加。不同输入信噪比下，可以得到相邻脉冲相位差的离差与判决门限的关系图，选取输入信噪比为7 dB时，得到如图2所示的相邻脉冲相位差的离差与判决门限的关系图，从图2中可以看出，选取一定的k值即确定门限值，根据落入门限的个数就可以确定信号相参性的识别准确率。

仿真实验2：假设侦察接收一串脉冲个数为P=2 000的非相参脉冲信号，脉冲幅度A=1，采样频率为fs=100 MHz，脉冲重复间隔为Tr=100 μs，信号的频率为f=30 MHz，脉冲宽度为τ=2 μs，脉冲信号的初始相位为φp，φp是(-π,π)内均匀分布的随机变量。取k=2.6～3.0[11]，即可确定判决门限T，按照设置的判决门限，判别脉冲串中相邻脉冲相位差的离差是否在判决门限内，根据落入判决门限的个数来计算非相参信号识别的准确率。不同输入信噪比下，实验独立仿真100次，不同输入信噪比下非相参信号识别准确率见表2，输入信噪比为 7 dB 时相邻脉冲相位差的离差,如图3所示。

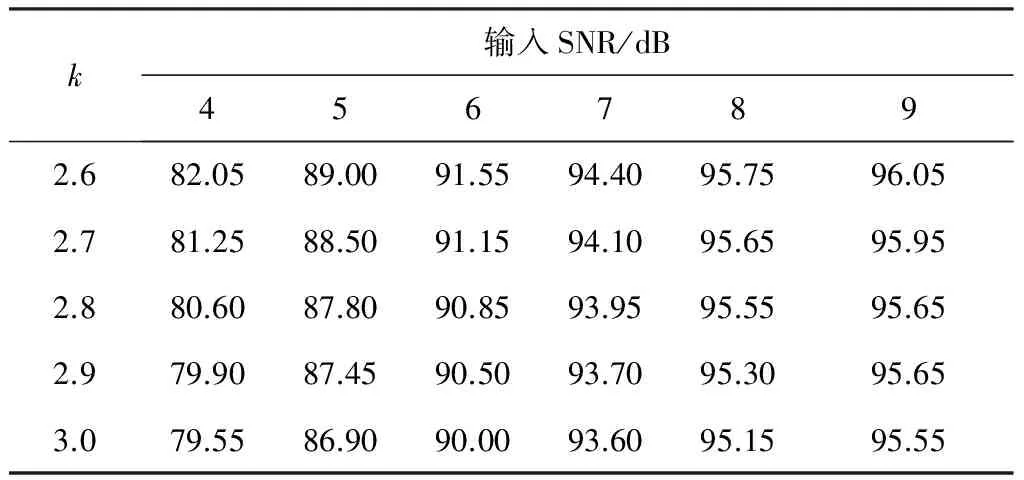
表2 不同输入信噪比下非相参信号识别准确率(%)

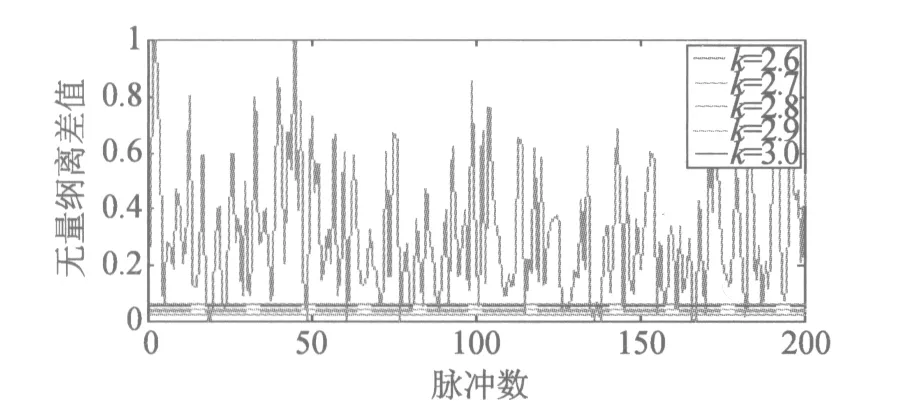
图3 输入信噪比为7 dB时相邻脉冲相位差的离差

从表2中可以看出，随着输入信噪比的增加，非相参信号的识别准确率逐渐增加，达到一定信噪比后，识别准确率达到90%以上。随着k值的增加，门限值增大，非相参信号的识别准确率逐渐降低。不同输入信噪比下，可以得到相邻脉冲相位差的离差与判决门限的关系图，选取输入信噪比为7 dB时，得到如图3所示的相邻脉冲相位差的离差与判决门限的关系图，从图3中可以看出，选取一定的k值即确定门限值，根据落入门限的个数就可以确定信号相参性的识别准确率。

综合以上的分析及仿真实验结果可知，由于噪声的影响，有部分相邻脉冲相位差的离差落入判决门限外。当输入信噪比大于7 dB时，相参信号的识别准确率可达99%以上，非相参信号的识别准确率可达90%以上。因此，通过判断相邻脉冲相位差的离差是否落入判决门限，可以判别脉冲相位跳变情况，实现脉冲相位线性度的检测，进而识别信号的相参性，这一相参特征可以应用于雷达辐射源信号分选中，实现高效准确的雷达辐射源信号分选。

3 分选算法及仿真分析

3.1 分选特征参数的提取

信号分选特征参数的选取，必须满足普遍性和稳定性[15]。显然，研究的脉冲相位线性度是信号相参特征的一种表现形式，不会因脉冲参数的改变而发生变化，因此脉冲相位线性度具有不因脉冲参数变化而改变的特点，满足普遍和稳定的适用性，可以将脉冲相位线性度用于区分任意两个脉冲是否相参。经过大量的仿真实验得出：选取一定的k值，可以确定判决门限来识别脉冲的相位线性度。对于k值选取过小，易产生“增批”现象；对于k值选取过大，易产生“漏批”现象。因此，根据2.3节中的分析，经过多次仿真实验分析，将k=2.6～3.0作为判决门限的系数，确定k值就可以确定判决门限，并利用确定的判决门限值来区分脉冲信号中任意两个脉冲是否相参。

3.2 分选算法

如果脉冲i和脉冲j来自于同一雷达辐射源，则脉冲i和脉冲j是相参的；如果脉冲i和脉冲j来自于不同雷达辐射源，则脉冲i和脉冲j是非相参的。综合以上的分析，基于脉冲相位线性度，可以实现雷达辐射源信号分选。

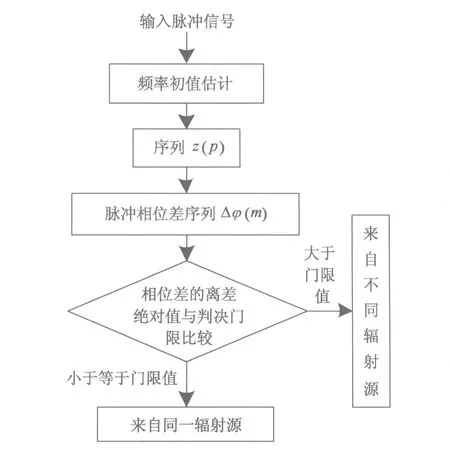
图4 分选算法流程图

本算法的流程,如图4所示，具体步骤为：

Step2 利用得到的频率初估计值构造序列，取共轭，再与侦收的信号相乘，得到序列k(p)，将序列k(p)进行脉内累加，得到序列z(p)；

Step3 将序列z(p)中任意两个脉冲共轭相乘，并检测共轭相乘序列的相位，得到 [p(p-1)]/2个脉冲相位差序列Δφ(m)m=1,…,[p(p-1)]/2；

Step4 计算序列Δφ(m)的离差序列y(m)，将离差绝对值与判决门限T比较。

Step5 若|y(m)|>T，可认为第m次相位检测时发生跳变，即第m次检测的两个脉冲是非相参的，来自不雷达同辐射源，否则可近似认为是线性的，即第m次检测的两个脉冲是相参的，来自同一雷达同辐射源。遍历离差序列，可以实现对脉冲信号的分选。

3.3 仿真分析

仿真实验条件设置：侦察接收一串脉冲信号，经过一次分选后，还有两个脉冲无法区分是否来自同一雷达辐射源。假设这两个脉冲属于不同雷达辐射源，这两个脉冲有相同的脉冲参数和近似相同的调制方式，利用现有的信号分选方法，即利用常规参数(载频、重频等)和脉内特征参数(频域特征参数、时频域特征参数等)，也无法判断这两脉冲是否来自同一雷达辐射源，造成分选的“漏批”现象。

仿真实验参数设置：脉冲幅度A=1，采样频率为fs=100 MHz，脉冲重复间隔为Tr=100 μs，信号的频率为f=30 MHz，脉冲宽度为τ=2 μs，脉冲的初始相位是(-π,π)内均匀分布的两个随机变量。选取不同的k值来设置判决门限，根据判决门限，判别两个脉冲相位差的离差是否在判决门限内，即检测脉冲相位的线性度，若是线性的，则两个脉冲是相参的，来自同一雷达辐射源，若是跳变的，则两个脉冲是非相参的，来自不同雷达辐射源。统计离差落入判决门限的次数来，求取雷达辐射源信号分选的准确率。不同k值和信噪比下，实验独立仿真100次，不同输入信噪比下分选准确率，见表3；不同的k值和输入信噪比下分选准确率，如图5所示。

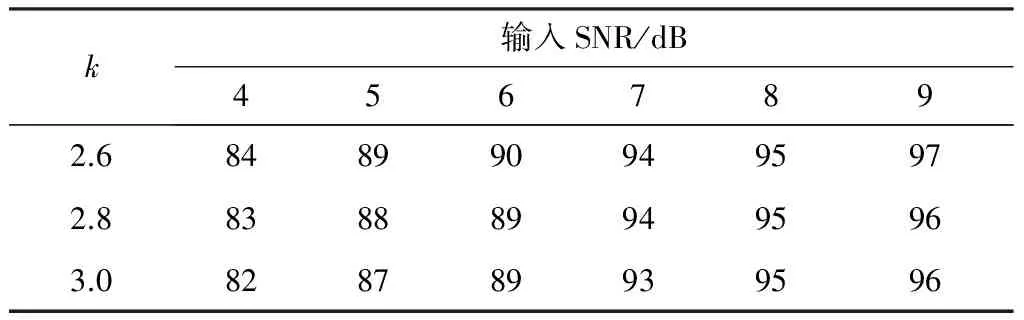
表3 不同输入信噪比下分选准确率(%)

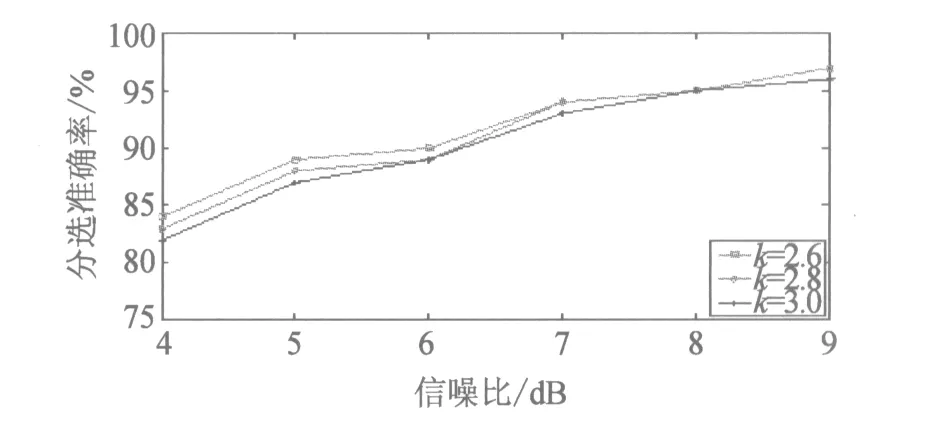
图5 不同的k值和输入信噪比下分选准确率

从表3和图5可看出，k值的不同是为了选取不同的门限值，基于脉冲相位线性度的分选方法对信号进行分选，分选准确率随着信噪比的增加而增加，在输入信噪比大于等于7 dB时分选准确率均大于90%，而使用现有分选方法在此仿真条件下，信号分选的准确率几乎为0。因此，基于脉冲相位线性度的分选方法，可以较好的解决信号分选中出现的分选“漏批”问题。

4 结 语

研究了基于脉冲相位线性度的雷达辐射源信号分选方法，对脉冲相位线性度进行检测，并进行仿真验证。最后给出了分选算法的步骤，并进行分选仿真分析，在较低输入信噪比情况下，可以实现雷达辐射源信号的准确分选，在电子情报侦察系统上有着广阔的应用前景。下一步可以将本方法应用于一串未知的脉冲信号中进行分选，以期待更好的使用性。

[1] 国强.雷达信号分选理论研究[M].北京:科学出版社.2010.

[2] ZHANG GEXIANG,RONG HAINA,HU LIZHAO.Entropy Feature Extraction Approach of Radar Emitter Signals[C]//Proceedings of International Conference on Intelligent Mechatronics and Automation,2004:621-625.

[3] ZHANG GEXIANG,JIN WEIDONG,HU LAIZHAO.Radar Emitter Signal Recognition Based On Complexity Features[J].西南交通大学学报:英文版.2004,12(2):116-122.

[4] 张葛祥,胡来招,金炜东.基于熵特征的雷达辐射源信号识别[J].电波科学学报.2005,20(4):440-445.

[5] 张葛祥,金炜东,胡来招.基于相像系数的雷达信号特征选择[J].信号处理.2005,21(6):663-667.

[6] ZHANG GEXIANG,JIN WEIDONG,HU LAIZHAO.Resemblance Coefficient Based Intrapulse Feature Extraction Approach for Radar Emitter Signals[J].电子学报：英文版,2005，14(2):337-341.

[7] 韩俊,何明浩,朱元清,等.基于双谱二维特征相像系数的雷达信号分选[J].电波科学学报.2009,24(5):848-853.

[8] 叶昊儒.相参雷达与非相参雷达的差异分析[J].现代电子技术,2010(3):17-19.

[9] 赵葆昶.利用相参特性的雷达辐射源信号分选方法研究[D].武汉:空军雷达学院.2010.

[10] 郁春来,占荣辉,万建伟.一种BPSK相参脉冲信号多普勒频率变化率测量方法[J].国防科技大学学报.2008,30(1):53-56.

[11] 胡嬿,刘渝.相参脉冲信号识别方法和性能分析[J].数据采集与处理.2012,27(3):314-319.

[12] Y L S H X.Modified Kay’s method with improved frequency estimation[J].Electronics Letters,2000,36(10):918-920.

[13] 张刚兵,刘渝,邓振淼.相参脉冲信号频率估计算法研究[J].电子学报.2009,37(9):2 058-2 061.

[14] KAY S.A fast and Accurate Single Frequency Estimator[J].IEEE Transactions on Acoustics Speech and Signal Processing,1989,37(12):1 987-1 990.

[15] 徐璟,何明浩,陈昌孝,等.雷达辐射源特征参数提取算法复杂度分析[J].中国电子科学研究院学报,2013(1):43-47.