关于不定方程x3+8=py2的整数解的研究

普粉丽

（普洱学院 数学与统计学院，云南 普洱 665000）

关于不定方程x3+8=py2的整数解的研究

普粉丽

（普洱学院 数学与统计学院，云南 普洱 665000）

设p=3(8k+5)(8k+6)+1(k∈N)为奇素数，利用初等方法证明了不定方程x3+8=py2无gcd(x,y)=1的正整数解的一个充分条件。

不定方程；奇素数；正整数解；同余式

方程

x3+8=Dy2(x,y ∈N,D＞0，且无平方因子) (1a)是一类重要的不定方程，其整数解已有不少人研究过。

当D含素因素3时，1981年柯召、孙琦[1]证明了D不能被3或6k+1形的素因子整除时，若D≡1,9(mod 20)，则方程

无非平凡整数解；曹玉书[2]给出了D含6k+1型素因子时方程x3-8=3Dy2无非平凡整数解的一些充分性条件；1992年，曹玉书、黄龙铉[3]给出了D含6k+1型素因子时方程

无非平凡整数解的一些充分条件；2004年，乐茂华[4]给出了方程

无gcd(x,y)=1的正整数解的一个充分条件；2010年，韩云娜等[5]给出了D含6k+1型素因子时方程

无非平凡整数解的一些充分条件。

当D不含素因素3时，1981年柯召、孙琦[1]证明了D不能被3或6k+1形的素因子整除时，若D≡0,1,2(mod4)，则方程(1c)仅有整数解(x, y)=(2,0)；2004年，乐茂华[6]给出了方程

无gcd(x,y)=1的正整数解的一个充分条件；2009年，占金虎[7]给出了方程(1f)无gcd(x,y)=1的正整数解的一个充分条件；2012年，霍梦圆[8]给出了方程

的所有解。本文给出了D含6k+1型素因子时方程(1f)无正整数解的一个充分条件。

定理若p=3(8k+5)(8k+6)+1(k∈N)为奇素数，则不定方程(1f)无gcd(x,y)=1的正整数解。

证明因为gcd(x,y)=1，故x≡/0(mod2)，所以方程(1f)可分

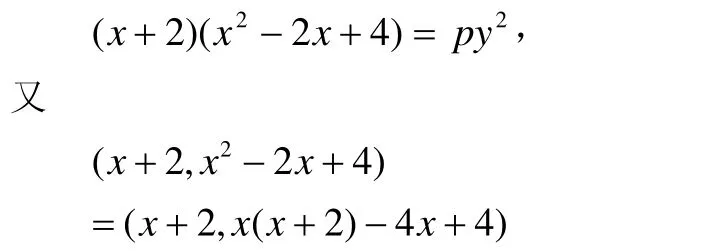
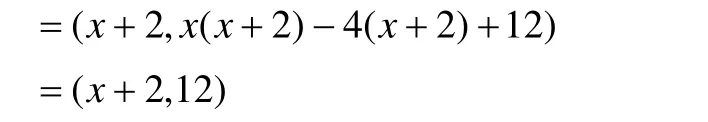
而12的正约数有1,2,3,4,6,12，且x ≡/0（mod2），即x+2≡/0（mod 2）。故(x+2,x2-2x +4)=1或3。由此可见，方程(1f)可以分解为以下四种情形：

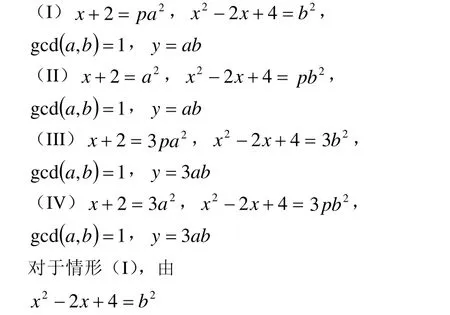
配方得

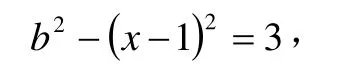
解得x=2或x=0。把x=2代入x+2=pa2得pa2=4，又a2≥0，且

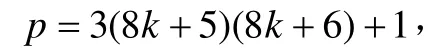
所以p≡3(mod8)，所以pa2=4不成立。把x=0代入x+2=pa2同理可得不成立。所以对于情形（I），不定方程(1f)无gcd(x,y)=1的正整数解。

对于情形（II），因为x ≡/0(mod2)，则x一定是奇数，那么x+2和x2-2x+4也一定是奇数。又x+2=a2,所以a2也是奇数，故a2≡1(mod8)，所以

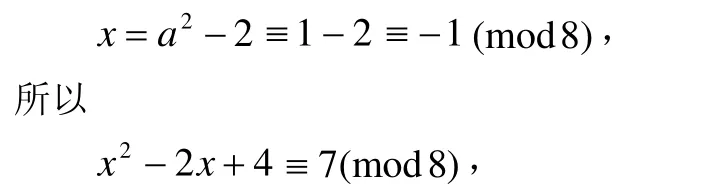
又x2-2x+4=pb2，x2-2x+4和p是奇素数，所以b2≡1(mod8)，又p≡3(mod8)，所以pb2≡3(mod8)，因此有

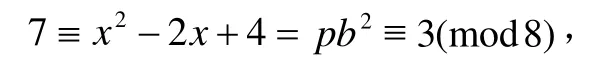
矛盾。所以对于情形（II），方程(1f)无gcd(x,y)=1的正整数解。

对于情形（III），因为x≡/0(mod2)，则x一定是奇数，那么x+2和x2-2x+4也一定是奇数。又x+2=a2，则a2也是奇数，故a2≡1(mod8)，所以

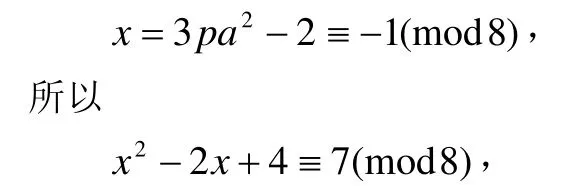
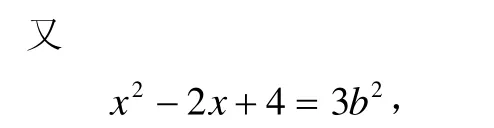
又b2≡1(mod8)，所以3b2≡3(mod8)，则

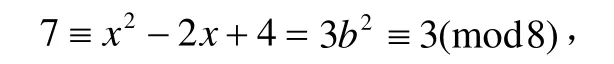
矛盾。所以对于情形（III），方程(1f)无gcd(x,y)=1的正整数解。

对于情形（IV），因为x ≡/0(mod2)，则x一定是奇数，那么x+2和x2-2x+4也一定是奇数。又x+2=3a2，所以a2也是奇数，故a2≡1(mod8)，由x+2=3a2知x=3a2-2，即x≡1(mod8)，所以

其中x2-2x+4也是奇数，所以

b2≡1(mod8)，3b2≡3(mod8)，

又p≡3(mod8)，所以

1≡3pb2=x2-2x +4≡3(mod8)，

矛盾。所以对于情形（IV），不定方程(1f)无gcd(x,y)=1的正整数解。

综合以上四种情形，若

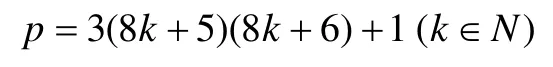
为奇素数，则不定方程

x3+8=py2无gcd(x,y)=1的正整数解。

[1] 柯召,孙琦.关于丢番图方程x3±8=Dy2和x3±8= 3Dy2[J].四川大学学报(自然科学版),1981(4):1-5.

[2] 曹玉书.关于丢番图方程x3±8=3Dy2[J].黑龙江大学学报自然科学学报,1991,8(4):18-21.

[3] 曹玉书,黄龙铉.关于丢番图方程x3±8=3Dy2[J].黑龙江大学学报自然科学学报,1992,9(2):3-5.

[4] 乐茂华.关于Diophantine方程x3+8=3py2[J].宁德师专学报,2004,16(4):347-349.

[5] 韩云娜,赵春华.关于Diophantine方程x3±8=3Dy2[J].四川理工学院学报(自然科学版),2010,23(2):156-157.

[6] 李娜.关于Diophantine方程x3±8=Dy2[J].四川理工学院学报(自然科学版),2011,24(5):593-595.

[7] 占金虎.关于Diophantine方程x3±8=Dy2[J].科学技术与工程:2009,9(1):91-93.

[8] 霍梦圆.关于不定方程x3+8=73y2[J].重庆师范大学学报(自然科学版),2012,3(11):18-20.

（责任编辑、校对：赵光峰）

On the Integer Solution of the Indeterminate Equation x3+8=py2

PU Fen-li
(College of Mathematics and Statistics, Puer University, Puer 665000, China)

Letp=3(8k+5)(8k+6)+1(k∈N)be an odd prime. By using the elementary method, the sufficient condition of positive integer solution is proved on the condition that the indeterminate equation x3+8=py2(x,y∈N) has no integer solutions with gcd(x,y)=1.

indeterminate equation; odd prime; positive integer solution; congruence;

O156

A

1009-9115(2014)02-0016-02

10.3969/j.issn.1009-9115.2014.02.004

2013-10-03

普粉丽（1980-），女，云南江川人，硕士，讲师，研究方向为初等数论及数学教育。