基于NSGA-II遗传算法的磁流变悬置多目标优化
2014-02-05段绪伟李以农邓召学
段绪伟,李以农,郑 玲,邓召学
(重庆大学 机械传动国家重点实验室,重庆 400044)
基于NSGA-II遗传算法的磁流变悬置多目标优化
段绪伟,李以农,郑 玲,邓召学
(重庆大学 机械传动国家重点实验室,重庆 400044)
磁流变悬置集总参数优化是设计高性能发动机悬置的关键。为克服以往悬置优化中优化目标单一、优化目标选取不合理、未考虑实际加工可行性等问题,建立单自由度磁流变悬置隔振系统数学模型,提出倍程区间灵敏度分析法,对各集总参数灵敏度进行分析,并以此为依据选取优化变量。以发动机常用转速激振频率段的力传递率积分为优化目标,采用改进型非支配排序遗传算法(NSGA-II)进行多目标优化。在一定范围内将结构尺寸进行离散化处理,计算各组离散尺寸对应的集总参数值,以离散集总参数与集总参数Pareto非劣解之间的综合距离为准则筛选最优解。
磁流变悬置;集总参数;优化;倍程区间灵敏度;NSGA-II算法
磁流变液是近年来研究较多的新型智能材料,它通常是由非磁性载体液、磁性微粒和稳定剂组成的两相悬浮液体,其基本特征:在外加磁场作用下,能在瞬间从自由流动的液体转变为半固体,呈现可控的屈服强度,而且这种变化是可逆的[1]。利用磁流变液的这种流变特性,Ciocanel等[2]设计了混合模式的磁流变悬置,并对其低频动特性进行了理论和实验研究;Choi等[3]设计了混合模式磁流变悬置,对其在结构振动控制中的应用进行了相关研究;Farjoud等[4]设计了挤压模式磁流变悬置,对其磁路等进行了研究;王雪婧[5]、魏付俊[6]、李锐[7]对不同形式磁流变悬置的动特性进行了研究。
在悬置优化设计方面,Ahn等[8]以普通液压悬置隔振力传递率各极值点及其发生频率的加权组合为优化目标,采用EALA法进行单目标优化,但优化效果受权重系数影响大,且几个频率点上传递率的叠加不能很好地反映隔振系统的隔振效果。Li等[9]以普通液压悬置动刚度及阻尼滞后角在特征频率处取值的加权组合为优化目标,在获得其实验数据的基础上,采用基因神经网络算法对悬置动特性进行单目标优化,其神经网络训练的好坏依赖于实验数据准确性,对于悬置初期设计不适用。且目前很少有针对磁流变悬置进行多目标优化的研究,而优化对于获得具有良好隔振性能的磁流变悬置尤为重要,因此对磁流变悬置集总参数进行优化具有重要的工程意义。
1 磁流变悬置隔振
1.1 磁流变悬置结构及工作原理
本文设计了新型流动模式磁流变悬置,其结构示意图如图1所示。主要由橡胶主簧8、扰流盘9、磁芯内上1、磁芯外上3、磁芯内下6、磁芯外下5、电磁激励线圈11、可控阻尼通道2、解耦膜4、上液室10、下液室7以及橡胶底膜12等组成。
低频大振幅激振时,橡胶主簧发生变形,上液室压力变化,使磁流变液流经可控阻尼通道。利用磁流变液的流变特性,调节激励线圈电流大小控制可控阻尼通道有效磁极对应处的磁场强度,即可调节其屈服强度,实现可控阻尼通道液阻调控,从而调控磁流变悬置低频动态特性。浮动式解耦膜与解耦器隔板之间间隙小,此时因激振频率低、激振幅值大,解耦膜“阻断”解耦器,使流经解耦器的流量极少[10]。高频小振幅激振时,在扰流盘扰流作用下,与扰流盘相邻的区域紊流度增加,使得解耦膜在其平衡位置附近振动,部分磁流变液流经解耦器,缓解上下液室压力波动,有效抑制悬置高频动态硬化,可改善磁流变悬置高频动态特性。

图1 磁流变悬置结构示意图Fig.1 Structural sketch of MR mount

图2 单自由度隔振力学模型Fig.2 Mechanical model of vibration isolation
1.2 磁流变悬置集总参数模型
为研究磁流变悬置隔振性能,建立含磁流变悬置集总参数的单自由度隔振系统力学模型,如图2所示。
Me为单个悬置支撑的等效发动机质量,Kr、Br分别为橡胶主簧的静刚度和阻尼,C1、C2分别为上、下液室的体积柔度。Ap、Ad分别为橡胶主簧等效活塞面积、解耦膜面积,Im、Id分别为可控阻尼通道的液感、解耦器液感,Rm(I)、Rd分别表示可控阻尼通道的液阻、解耦器液阻。通过可控阻尼通道、解耦器的流量分别为Qm(t)、Qd(t)。上、下液室的压力分别为P1(t)、P2(t)。Xe(t)为发动机振动位移激励,F(t)为传递给基体的力。
低频大振幅激振时,通过解耦器的磁流变液极少,高频小振幅激振时,通过可控阻尼通道的磁流变液也极少,两者均可忽略。利用流体力学理论等,可推导出悬置低频复刚度式(1)及力传递率式(2),悬置高频复刚度式(3)及力传递率式(4)。

式中:Rm(I)=Rm0+RIm,Rm0为可控阻尼通道零场粘性液阻=6lcζ(NI/2g)τ/为屈服液阻,lc为有效磁极长度,N、I分别为激励线圈的匝数和电流,g为通道间隙,Qm为通道流量,ζ、τ为磁流变液属性参数[5],KL1、KH1、KL2、KH2分别为低、高频复刚度的实部和虚部,TLF、THF分别为低、高频悬置力传递率。
2 隔振优化问题
为有效隔离发动机的振动向车架传递,磁流变悬置隔振系统力传递率峰值、怠速工况激振以及常用高转速激振时力传递率都应尽可能小,力传递率峰值发生频率应避开发动机怠速工况,同时各集总参数的取值范围受实际结构等因素制约。因此,本文以低频段(f1,f2)=(6 Hz,30 Hz)和高频段(f3,f4)=(100 Hz,200 Hz)的力传递率积分值作为目标,以峰值、峰值发生频率和集总参数的取值为约束条件进行优化,则优化问题可描述如下:

其中:TL(f,X)、TH(f,X)分别为低、高频传递率,TL_max为低频力传递率最大值,fL_max为低频力传递率最大值发生频率,X为含各集总参数的优化变量,X0为各集总参数初始值,K1、K2为集总参数取值范围的系数矩阵。
3 选取优化变量
磁流变悬置集总参数的调节,可通过调整结构尺寸、橡胶硬度、激励线圈匝数、激励电流大小等来实现,但受尺寸、加工可行性、密封要求等限制,以最小的调整获得最佳的参数匹配尤为重要,为此通过集总参数的灵敏度分析各参数对隔振性能的影响程度,并以此为依据选取合适的优化变量。
3.1 倍程区间灵敏度法
集总参数的物理意义各异,参数值数量级相差大,参数变化范围大,且具有较强的非线性。利用差分法、摄动法等常规灵敏度分析法计算的灵敏度值可比性差、可信度低。针对集总参数的特点,采用倍程区间灵敏度分析法对集总参数的灵敏度进行分析,此法是对区间灵敏度法[12]的改进,即将集总参数摄动范围进行倍程化处理,利用区间数学计算其相对灵敏度。该法对参数变化量Δx的选择比差分法要求低,且求解非单调非线性问题灵敏度的结果比差分法更合理。倍程区间灵敏度分析法简述如下:

3.2 集总参数灵敏度分析
为分析磁流变悬置的各集总参数对隔振性能的影响,可等价转换为各集总参数对优化目标F1和F2的倍程区间灵敏度,由此便可选出合适的优化变量。
针对某型号发动机,参考原液压悬置设计流动模式磁流变悬置,其集总参数初始值如表1所示。根据集总参数初始值,采用倍程区间灵敏度法,利用MATLAB编程可计算各集总参数对优化目标F1和F2的倍程区间灵敏度值。为具有可比性,各参数的区间倍程化系数均为β=0.1,结果如表2和表3所示。

表1 磁流变悬置集总参数初始值Tab.1 Lumped parameters of original MR mount

表2 集总参数对F1的倍程区间灵敏度值Tab.2 Multiple interval sensitivity of lumped parameters

表3 集总参数对F2的倍程区间灵敏度值Tab.3 Multiple interval sensitivity of lumped parameters
从计算的倍程区间灵敏度值可知,各集总参数对目标F1的灵敏度绝对值由大到小为Ap>C1>Rm>Kr>Im>C2>Br>Rd=Id=0,各集总参数对目标 F2的灵敏度绝对值由大到小为Kr>C1>Rd>Ap>Id>C2>Br>Rm=Im=0。参数C2、Br的灵敏度绝对值很小,即表明其对隔振性能的影响很小,可不予考虑。
4 集总参数优化
为实现集总参数的多目标约束优化,本文借鉴具有较高计算性能和较少人工经验参与的非支配排序遗传算法NSGA-II,并针对磁流变悬置的集总参数取值等特点,改进NSGA-II遗传算法,使之适用于该问题。
4.1 NSGA-II遗传算法及其改进
非支配排序遗传算法(NSGA-II)是Deb对Srinivas所提出的NSGA算法的改进[14],相对于NSGA算法具有以下优越性:① 计算复杂度由O(mN3)降低为O(mN2)。其中,m为目标函数个数;N为种群规模。② 引入精英策略,可保留父代精英个体,且无需人为确定共享半径参数。③ 采用拥挤度比较算子使种群具有多样性。
采用非支配排序遗传算法(NSGA-II)进行优化时,由于磁流变悬置集总参数的数量级相差大,若采用二进制编码,染色体长度骤增,计算量大;若采用实数编码,计算精度受到限制,且采用标准NSGA-II遗传算法进行优化时未考虑约束条件。因此,本文对标准的非支配多目标遗传算法进行以下改进:① 在进行遗传算子之前对变量X进行同级化处理XR=RX,其中R=diag(r1,r2,r3...r7)=diag(103,10-5,1011,10-5,10-8,10-4,10-7)为同级化转换对角矩阵,ri为第 i个参数同级化因子。在完成遗传算子操作后,还原参数值进行适应度计算。②在选择个体时,增加判断个体是否满足约束条件的环节,若满足则保留,反之则直接淘汰。改进后的算法流程如图3所示。
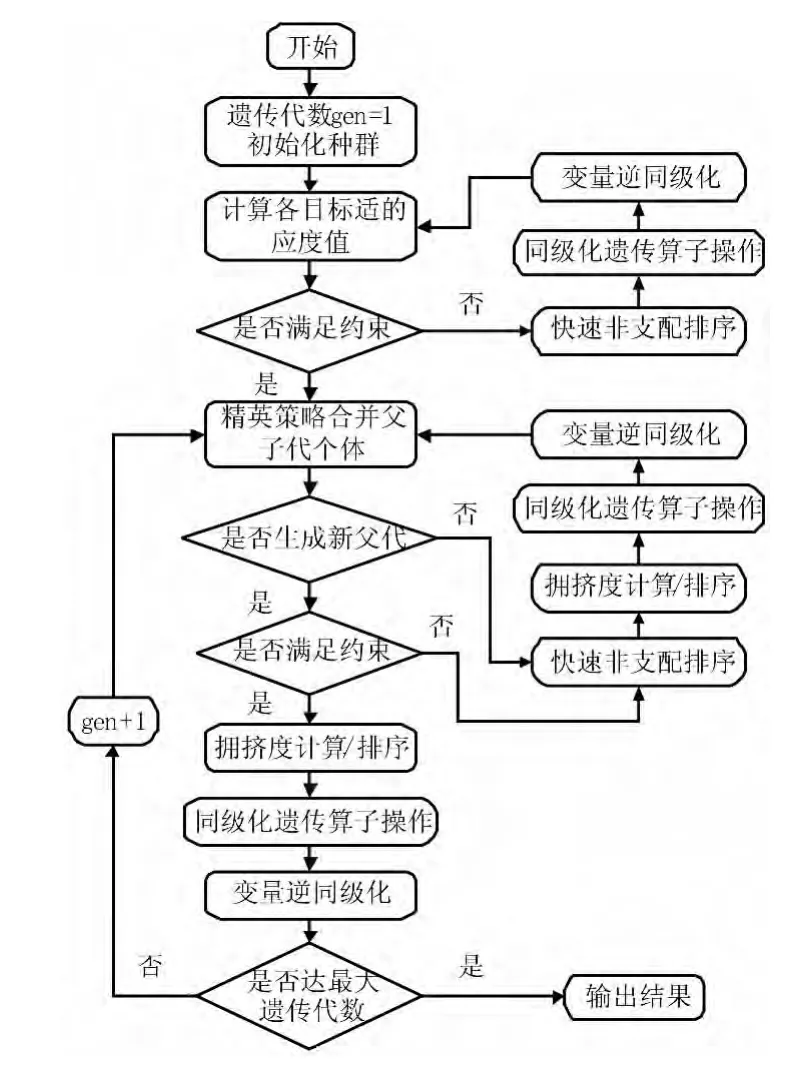
图3 改进型NSGA-II算法流程图Fig.3 Process of improved NSGA-II algorithm
4.2 优化计算
在磁流变悬置的集总参数中,Ap、Kr、C1对磁流变悬置隔振性能影响较大,且通过调节结构尺寸可使其在较大范围内变化,其倍程系数β可设置较大。可控阻尼通道的液阻Rm与液感Im、解耦器的液阻Rd与液感Id分别为同一结构的不同集总参数,为两对非独立参数。
此外,因可控阻尼通道液阻随激励电流的增大而增大,而液感基本不变,且Lr(Rm)≈Lr(Im),为实现两者的匹配,则倍程系数β(Rm)应略大于β(Im);解耦器液阻Rd与液感Id不受激励电流影响,Lr(Rd)>Lr(Id),为实现两者的匹配,则倍程系数 β(Rd)应略大于β(Id)。因此,集总参数取值范围的系数对角化矩阵可设置为:
K1=diag(0.7,0.7,0.7,0.7,0.65,0.75,0.7)
K2=diag(1.3,1.3,1.3,1.3,1.35,1.25,1.3)
根据磁流变悬置初始结构的集总参数,利用MATLAB编写改进型NSGA-II算法进行优化计算,在频域区间内求解力传递率积分时,采用4节点Newton-Cotes公式进行数值积分,设置种群大小为100,遗传代数为300代,优化后所得 Pareto非劣解集前沿面如图4所示。

图4 Pareto非劣解集前沿面Fig.4 The Pareto solution frontier
4.3 筛选Pareto非劣解集中的最优个体
考虑结构尺寸限制、加工精度、结构布局合理性以及密封要求等实际问题,在筛选经优化所得的非劣解集中最优个体时,由各集总参数关于结构尺寸以及流体属性的计算公式[5,15],根据实际结构可取的离散尺寸值,可获得各集总参数与实际结构尺寸相对应的取值离散集,然后计算所有Pareto非劣解个体的个体综合距离DR,以个体综合距离DR最小值个体作为最优个体。考虑到各集总参数的倍程区间灵敏度以及各集总参数量级不一致等因素,定义同级化个体综合距离DR如下:


其中:Y表示独立集总参数 Ap、Kr、C1,rY表示独立集总参数Y的同级化因子。Yj为离散集中与第j组尺寸对应的集总参数值,YPi为Pareto非劣解集中第i个个体对应的集总参数值,j=1,2,3…n,i=1,2,3…k,n 为离散尺寸组数。

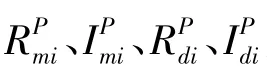

图5 液阻Rm液感Im组离散集和Pareto集Fig.5 Fluid Rm|Imin discretization and Pareto set

图6 Pareto集个体综合距离Fig.6 Synthesized distance of Pareto set’s individuals
根据个体综合距离公式(7),可计算改进型NSGA-II算法多目标优化所得的Pareto非劣解集中每个个体的个体综合距离,选取个体综合距离最小个体作为最符合实际结构要求的最优个体。Pareto非劣解集中每个个体的个体综合距离DiR如图6所示,与最优个体对应的同级化集总参数值如图7所示。
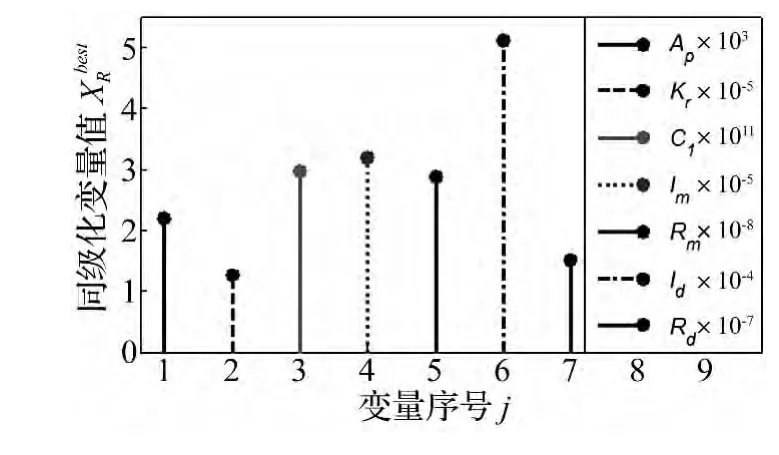
图7 最优个体同级化值Fig.7 Peer parameter value of the best individual
4.4 最优隔振性能及悬置最优动特性
根据综合距离准则选取的最优集总参数,由式(2)编写MATLAB程序可得磁流变悬置隔振系统低频最优力传递率,如图8所示。

图8 低频力传递率对比Fig.8 Contrast the force transmissibility in low frequency range
由图8可知,优化后低频大振幅激振时隔振总体效果优于原结构。优化后的力传递率峰值TLmax由3.07降为2.564,峰值发生频率fLmax由 8.8 Hz 降为 7.2 Hz。优化后的力传递率在0~7.36 Hz内略大于原结构,而在7.36~50 Hz内明显小于原结构。
最符合实际结构要求的最优集总参数组中,可控阻尼通道的液阻Rm0是零磁场粘性液阻,而Rm(I)=Rm0+RIm随激励电流增大而呈非线性增大。因此,由式(1)和(2)进行MATLAB编程可得磁流变悬置集总参数最优化后的低频力传递率曲面以及此时磁流变悬置的动态特性曲面,分别如图9、图10和图11所示。
从图9低频传递率曲面中可知,随着激励电流的增大,力传递率峰值呈先减小后略增大变化趋势,峰值发生频率基本不变。在实际运用中,为获得低频段最优的隔振效果,可由转速传感器采集发动机实时转速,计算其二阶激振频率,以该激振频率下传递率最小的激励电流作为最优控制电流Iopt(f),从而实现磁流变悬置低频大振幅激振时的最优隔振控制。
从图10和图11可知,在最优激励电流Iopt(f)下可得的磁流变悬置最优动态特性,这为设计具有优良隔振性能的磁流变悬置提供了动特性最优目标,具有一定的参考价值。
诸多研究表明,发动机悬置隔振系统对悬置的理想特性要求是:低频大振幅激振时悬置应具有高刚度大阻尼特性,高频小振幅激振时应具有低刚度小阻尼特性[16]。因此,在高频小振幅激振时,磁流变悬置不施加激励电流,而通过扰流盘的扰流作用使更多的磁流变液流经解耦器,缓解高频动态硬化,从而获得较小的动刚度和阻尼滞后角,便可使磁流变悬置隔振系统具有更理想的隔振效果。由优化后所得的解耦器最优液阻Rd与液感Id参数,根据式(4)编程可得磁流变悬置隔振系统高频最优力传递率曲线,如图12所示。

图9 低频力传递率曲面Fig.9 Curved surface of force transmissibility in low frequency range

图10 低频悬置动刚度曲面Fig.10 Curved surface of dynamic stiffness in low frequency range

图11 低频悬置阻尼滞后角曲面Fig.11 Curved surface of loss angle in low frequency range
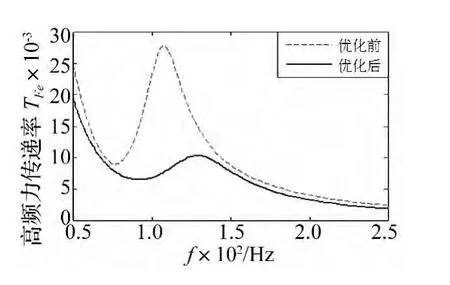
图12 高频力传递率对比Fig.12 Contrast the force transmissibility in high frequency range
由图12可知,优化后高频激振时隔振效果优于原结构,优化后力传递率峰值THmax由0.030 1降为0.010 3,峰值发生频率fHmax由107.2 Hz增为128.8 Hz。优化后的力传递率在50~75 Hz内略小于原结构,在75~139 Hz内明显小于原结构,在139~250 Hz内略小于原结构。
5 结论
本文建立了磁流变悬置隔振系统的等效集总参数模型,推导了磁流变悬置复刚度和力传递率的解析式,提出倍程区间灵敏度分析法,通过集总参数灵敏度分析,确定了磁流变悬置隔振系统的优化变量,以常用转速激振频率力传递率积分为目标函数,采用改进型非支配排序遗传算法(NSGA-II),对磁流变悬置隔振系统参数进行了多目标优化,提出了以个体综合距离来衡量Pareto非劣解集中个体优越性的方法。研究结果表明:本文提出的倍程区间灵敏度分析法和多目标优化方法是正确、可行的,优化后的悬置隔振系统,无论在低频段还是高频段,隔振效果均明显优于原系统,为磁流变悬置隔振系统的优化设计提供了科学方法与手段。在实际中,应提高加工和装配的精度、控制橡胶主簧硬度、选用性能稳定的磁流变液等,从而使悬置的各集总参数与最优值尽可能一致。
[1] Olabi A G,Grunwald A.Design and application of magnetorheological fluid[J].Materials and Design,2007,28:2658-2664.
[2] Ciocanel C,Nguyen,Elahinia M.Design and modeling of a mixed mode magnetorheological(MR)fluid mount[C].Active and Passive Smart Structures and Integrated Systems,2008,6928:69281C1-69281C10.
[3]Choi S B,Hong S R,Sung K G,et al.Optimal control of structural vibrations using a mixed-mode magnetorheological fluid mount [J]. InternationalJournalofMechanical Sciences,2008,50(3):559-568.
[4]Farjoud A, CraftM, BurkeW, etal. Experimental investigation ofMR squeeze mounts [J]. Journalof Intelligent Material Systems and Structures,2011,22:1645-1652.
[5]王雪婧.磁流变半主动发动机悬置隔振性能与控制方法研究[D],长春:吉林大学,2011.
[6]魏付俊.汽车动力总成磁流变悬置的设计和半主动控制研究[D],南京:南京航空航天大学,2007.
[7]李 锐.基于磁流变液悬置的发动机隔振方法与试验研究[D],重庆:重庆大学,2009.
[8] Ahn Y K,Song J D,Yang B S.Optimal design of engine mount using an artificial life algorithm[J].Journal of Sound and Vibration,2003,261:309 328.
[9]Li Q,Zhao J C,Zhao B,et al.Parameter optimization of a hydraulic engine mount based on a genetic neural network[J].Proceedings of the Institution of Mechanical Engineers,Part D:Journal of Automobile Engineering,2009,223(9):1109-1117.
[10] Singh R, Kim G, Ravindra P V.Linearanalysisof automotive hydro-mechanical mount with emphasis on decoupler characteristics [J]. JournalofSound and Vibration,1992,158(2):219-243.
[11] Ahn Y K,Song J D,Yang B S,et al.Optimal design of nonlinear hydraulic engine mount[J].Journal of Mechanical Science and Technology,2005,19(3):768-777.
[12]邱志平,王晓军.结构灵敏度分析的区间方法[J].兵工学报,2005,26(6):798 -802.
QIU Zhi-ping,WANG Xiao-jun.An interval method for sensitivity analysis of the structures[J].Acta Armamentarii,2005,26(6):798-802.
[13]沈祖和.区间分析方法及其应用[J].应用数学与计算数学,1983,2:1 -29.
SHEN Zhu-he. The method ofintervalanalysis and application [J].Communication on Applied Mathematics and Computation,1983,2:1-29.
[14]Kalyanmoy D,Amrit P,Sameer A,et al.A fast and elitist multi-objective genetic algorithm:NSGA - II [J].IEEE Transactions on Evolutionary Computation,2002,6(2):182-197.
[15] Nguyen,Ciocanel C,Elahinia M.Analytical modeling and experimental validation of a magnetorheological mount[C].Active and Passive Smart Structures and Integrated Systems,2009,7288:72881D1-72881D7.
[16] Kim G.Study of passive and adaptive hydraulic engine mount[D].Columbus:The Ohio State University,1992.
Multi-objective optimization for a MR engine mount based on NSGA-II algorithm
DUAN Xu-wei,LI Yi-nong,ZHENG Ling,DENG Zhao-xue
(State Key Laboratory of Mechanical Transmission,Chongqing University,Chongqing 400044,China)
To achieve a high performance,the design optimization of lumped parameters for a magneto-rheological(MR)engine mount is essential.Mathematical model of a single DOF vibration isolation system was established and the multiple interval sensitivity method was proposed to overcome drawbacks of conventional optimization designs,such as,single objective optimization,improper optimization objective,unfeasible machining and so on.Optimization variables in a MR engine mount were selected with a lumped parameter multiple interval sensitivity analysis.The integral of force transmissibility within normal frequency ranges of an engine was assigned as an objective function,the non-dominated sorting genetic algorithm(NSGA-II)was improved and used to optimize design variables.The synthesized distances between Pareto lumped parameters and discontinuous lumped parameters matching along with physical discretization dimensions were calculated to select the most appropriate solution from Pareto lumped parameters.
MR mount;lumped parameters;optimization;multiple interval sensitivity;NSGA-II algorithm
U463.33+
A
10.13465/j.cnki.jvs.2014.03.035
机械传动国家重点实验室项目(0301002109165)资助
2013-01-04 修改稿收到日期:2013-03-11
段绪伟 男,硕士生,1987年9月生
郑 玲 女,博士,教授,博士生导师,1963年生
